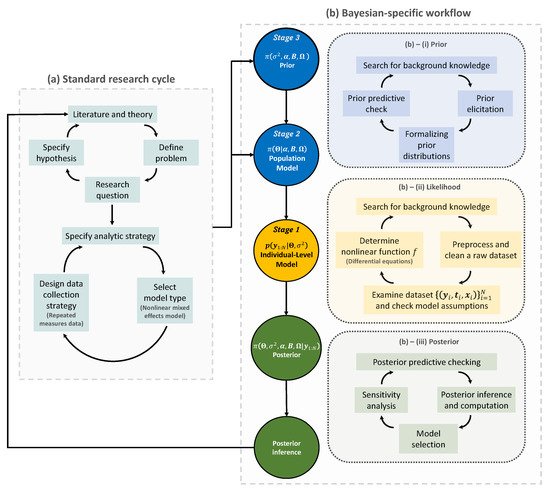
Figure 1. The Bayesian research cycle. A research cycle using Bayesian nonlinear mixed effects model comprises two steps: (a) standard research cycle and (b) Bayesian-specific workflow. Standard research cycle involves literature review, defining a problem and specifying the research question and hypothesis. Bayesian-specific workflow comprises three sub-steps: (b)–(i) formalizing prior distributions based on background knowledge and prior elicitation; (b)–(ii) determining the likelihood function based on a nonlinear function f; and (b)–(iii) making a posterior inference.
The first step of the Bayesian research cycle is (a) standard research cycle
[50][51][63,64]. Some early activities at this step involve reviewing literature, defining a problem, and specifying a research question and a hypothesis. After that, researchers specify which analytic strategy would be taken to solve the research question and suggest possible model types, followed by data collection. The data type arising in this process may include a response variable and some covariates that are grouped longitudinally, which then formulates repeated measures data of a population of interest. Furthermore, if there appears to be some nonlinear temporal tendency at each subject, then a possible model type for the analysis is a nonlinear mixed effects model
[15][52][15,65].
The second step of the Bayesian research cycle is (b) Bayesian-specific workflow. Logically, the first thing to do at this step is to determine prior distributions (see Step (b)–(i) in
Figure 1). The selection of priors is often viewed as one of the most crucial choices that a researcher makes when implementing a Bayesian model, as it can have a substantial impact on the final results
[53][66]. As exemplified earlier in the context of Bayesian medical device trials, using a prior in small sample studies may improve the estimation accuracy, but an unthoughtful choice of priors would lead to a significant bias in estimation. Prior elicitation effort would require Bayesian expertise to formulate domain expert’s knowledge in a probabilistic form
[54][67]. Strategies for prior elicitation include asking domain experts to provide suitable values for the hyperparameters of the prior
[55][56][68,69]. After prior is specified, one can check the appropriateness of the priors through prior predictive checking process
[57][70]. For almost all practical problems, prior distribution of Bayesian nonlinear mixed effect models can be hierarchically represented as follow: (1) a prior for the parameters used in likelihood, often called ‘population-level model’ in the literature of mixed effects modeling; and (2) a prior for the parameters used in the population-level model and for the parameters describing the residual errors used in likelihood. It is important to note that the former type of prior distribution (that is, (1)) is also a requirement to implement frequentist approaches for the nonlinear mixed effects model, as a name of ‘distribution for random effects’.
The second task is to determine the likelihood function (see Step (b)–(ii) in the panel). At
this time, the
raw dataset collected in (a) standard research cycle should be cleaned and preprocessed. Before
embarking on more serious statistical modeling, it is a common practice to get some insight about the research question via exploratory data analysis and have a discussion with domain experts such as clinical pharmacologists, clinicians, physicians, engineers, etc. To
some extent, eventually, all these efforts are to determine a nonlinear function
(denoted as f in this paper) that best describes the temporal profiles of all subjects. This nonlinear function is a
known function because it should be specified by researchers. In other words, the branch of the nonlinear mixed effects models belongs to parametric statistics. However, one technical challenge is that, in many problems, such a nonlinear function is represented as a solution of a differential equation system
[58][59][71,72], and
therefore there is no guarantee that
peoplewe can conveniently work with a closed-form expression of the nonlinear function. For
example, if
researchers wish to work with nonlinear differential equations
[60][61] [73,74], then some approximation via differential equation solver
[62][63][75,76] may be needed to calculate the nonlinear function. As such, most software packages dedicated to implementing a nonlinear mixed effect model, or, more generally, a Bayesian hierarchical model, are equipped with several built-in differential equation solvers
[17][37][64][17,47,77]. For instance, visit the website (
https://mc-stan.org/docs/2_29/stan-users-guide/ode-solver.html, accessed on 20 February 2022) to see some functionality supported in Stan
[17].
Finally, the likelihood is combined with the prior to form the posterior distribution (see Step (b)–(iii) in the panel). Given the important roles that the prior and the likelihood have in determining the posterior, this step must be conducted with care. The implementational challenge at this step is to construct an efficient MCMC sampling algorithm. The basic idea behind MCMC here is the construction of a sampler that simulates a Markov chain that is converging to the posterior distribution. One can use software packages if prior distributions to be implemented in Bayesian models exist in the list of prior options available in the packages
. Otherwise, professional programmers and Bayesian statisticians are needed to make codes manually; this review paper will be useful for that purpose.