Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Amina Yu and Version 5 by Amina Yu.
In two-fluid model (TFM), the granular flows are modeled as continuous fluid flows. The random motions of particles resulting from the interactive collisions of particles has a dominant effect on the flow behavior. The granular interactions are commonly modeled based on the kinetic theory of granular flow (KTGF).
- dense granular flow
- rotating drum
- flow and mixing
- two-fluid model
1. Introduction
Granular matter are ubiquitous in the daily lives and in industries, but they behave differently from other familiar forms of matter, such as solids, liquids and gases [1] [1]. Some researchers have even suggested that granular medium be considered as an additional form of substance existence [2]. The science of granular media has a long history [3], but the description of granular flow still remains an open issue due to its intriguing range of complex, nonlinear behavior. Because of their practicability and complexity, knowledge of the dynamics of particles is of high interest in engineering and academia. Among the many varieties of particle processing equipment, the rotating drum is a typical one with dense granular flow inside, and it is widely used in the industry for mixing, drying, milling, coating, or granulation/agglomeration [4] [4]. Particle flow in rotating drums exhibits a range of complex phenomena, such as avalanche, segregation, and convection [5]. Therefore, the current paper focus on dense granular flow in rotating drums.
The diameter of the rotating drum used in the industry ranges from a few meters to tens of meters, and the number of particles in it is huge. Therefore, the cost of industrial-scale experimental research is quite high. Moreover, it is difficult to get the particle scale information accurate in experiments [6]. With the rapid development of computers, numerical methods provide an effective and cost-saving alternative way to study particle flow behavior in rotating drums. The two common numerical methods are the discrete element method (DEM) and the two-fluid model (TFM). DEM has been applied in this area since the 1990s [7]. DEM calculates the motion and force equation of individual particles, so it can provide valuable particle scale information, such as coordinate number, collision velocity, and collision frequency [8].
2. Model Application
The behavior of particle flow is affected by many variables related to system geometry, operational condition, and material properties [7]. Rotational speed, which is an important operating parameter of the rotating drum, has attracted the attention of researchers for a long time. Ingram et al. [9][44] summarized the flow of dense particles in the rotating drum without flights at different rotational speeds into six patterns: sliding, collapsing, rolling, cascading, cascading, and centrifuging. In addition, the particles in the rotating drum are usually different in size, density and shape in practical application. However, only uniform particles with the same properties and binary particles with different sizes in rotating drums were found, as seen in Table 1.Table 1. Summary of the simulation condition.
| Year of Publication |
Focus of the Study | Validation Basis | Rotation Method | D (mm) |
L (mm) |
Flight or Not |
Particle Type |
d (mm) |
ρ | s | (kg/m | 3 | ) | Particle Shape |
|---|
| 2012 [10] | 2012 [45] | Dynamic characteristics and the rheology of a granular viscous flow scale up | Particle velocity and dimensionless active layer thickness | - | 400 | - | No | Uniform | 1.5 | 2900 | Spherical |
| 2013 [11] | 2013 [46] | Particle dynamic behavior | Solid flow regime and velocity distribution | - | 195 | 500 | No | Uniform | 1.09/3.68 | 2460 | Spherical |
| 2015 [12] | 2015 [17] | The effect of operating conditions on solids flow | Solids hold up in the flight | moving mesh | 108 | 500 | Yes | Uniform | 1.09/1.84/2.56 2.56 |
2455 2090 |
Spherical |
| 2016 [13] | 2016 [42] | Predict the transverse and axial solid-flow patterns, the fluid-flow profile, and particle residence time | Particle and fluid velocities and residence time | moving wall | 390 | 450 | No | Uniform | 4.25 | 1370 | Spherical |
| 2016 [14] | 2016 [47] | Heat transfer and mixing characteristics | Velocity and temperature of particles | - | 203 | - | No | Uniform | 2.5 | 2627 | Spherical |
| 2017 [15] | 2017 [27] | Boundary condition effects on the particle dynamic flow | Solids hold up in the flight, the bed height and solid volume fraction distribution | moving mesh | 108 | 500 | Yes | Uniform | 1.09 | 2455 | Spherical |
| 2017 [16] | 2017 [48] | The effects of specularity and restitution coefficients under different solid-flow regimes | Solid volume fraction distribution | moving mesh | 300 | 450 | Yes | Uniform | 25 | 7890 | Spherical |
| 2017 [17] | 2017 [49] | The effects of parameters on heat transfer characteristics | Average temperature of granular materials | moving wall | 300 | 350 | Yes | Uniform | 1 | 3900 | Spherical |
| 2018 [18] | 2018 [50] | The effects of parameters on the hydrodynamic and granular temperature of particles | Particle velocity | moving wall | 215 | - | No | Uniform | 6.2 | 1164 | Spherical |
| 2018 [19] | 2018 [51] | Irregular particle (non-spherical) dynamics | Rice grains velocities and drum transverse plane | moving wall and moving mesh | 390 | 20/30/40 | No | Uniform | 3.44 * | 1465 | Non-spherical |
| 2019[20] | 2019 [28] | The effects of parameters on the charge of solid in the flight | Solids hold up in the flight and solid volume fraction distribution | moving mesh | 108 | 500 | Yes | Uniform | 1.09 1.02 |
1551 963 |
Spherical |
| 2020 [21] | 2020 [10] | Solid frictional viscosity and wall friction | Particle velocity and flow pattern | moving mesh | 100 | - | No | Uniform | 3 | 2500 | Spherical |
| 2021 [22] | 2021 [52] | The comparison between the Eulerian (CFD) and the Lagrangian (DEM) approaches | Solids hold up in the flight and solid volume fraction distribution | moving mesh | 108 | 500 | Yes | Uniform | 1.09 | 2455 | Spherical |
| 2007[23] | 2007 [15] | Main features of solids motion and segregation | Particle velocity and concentration | - | 240 | 1000 | No | Binary | 1.5/3 | 2600 | Spherical |
| 2013[24] | 2013 [32] | Particle segregation and model of granular viscosity | End-view bed profile | - | 45 | 50 | No | Binary | 0.385/0.775 | 2500 | Spherical |
| 2016 [25] | 2016 [53] | Quantitatively and qualitatively evaluates the mixture and segregation processes | Drum transverse plane | - | 220 | 500 | No | Binary | 6.35/1.13 | 2460 | Spherical |
| 2017 [26] | 2017 [30] | Particle segregation and model of granular viscosity | End-view bed profile | - | 500 | 500 | No | Binary | 0.385/0.545/0.775 | 2500 | Spherical |
| 2017 [27] | 2017 [31] | Effects of specularity coefficient on particle segregation | End-view bed profile | - | 500 | 500 | No | Binary | 0.385/0.545/0.775 | 2500 | Spherical |
| 2020 [28] | 2020 [21] | Mixing and segregation of particles | The evolution of the degree of mixing and mixing process | - | 150 | 10 | No | Binary | 3/1.5 | 2600 | Spherical |
2.1. The Validation of the Model
An important step before using a model is validation. Usually, the model is validated by comparison with experiment results. Therefore, before the analysis of model application, how the model is validated is worthy of attention. A column named validation basis is given in Table 1. It is easy to see that for the drum with flights, solids holdup in the flight is often used as a comparison object. While for the drum without flight, the velocity distribution of particles is used the most, especially for drums with uniform particles. End-view bed profiles are used for rotating drums with binary particles inside because there is often a core structure of segregation, or other clear structures can be found, and it is easy to make qualitative comparison. It should be noted that the comparison using granular temperature is not found, although it is the most direct way for the validation of the model.2.2. Study on the Flow of Dense Uniform Particles
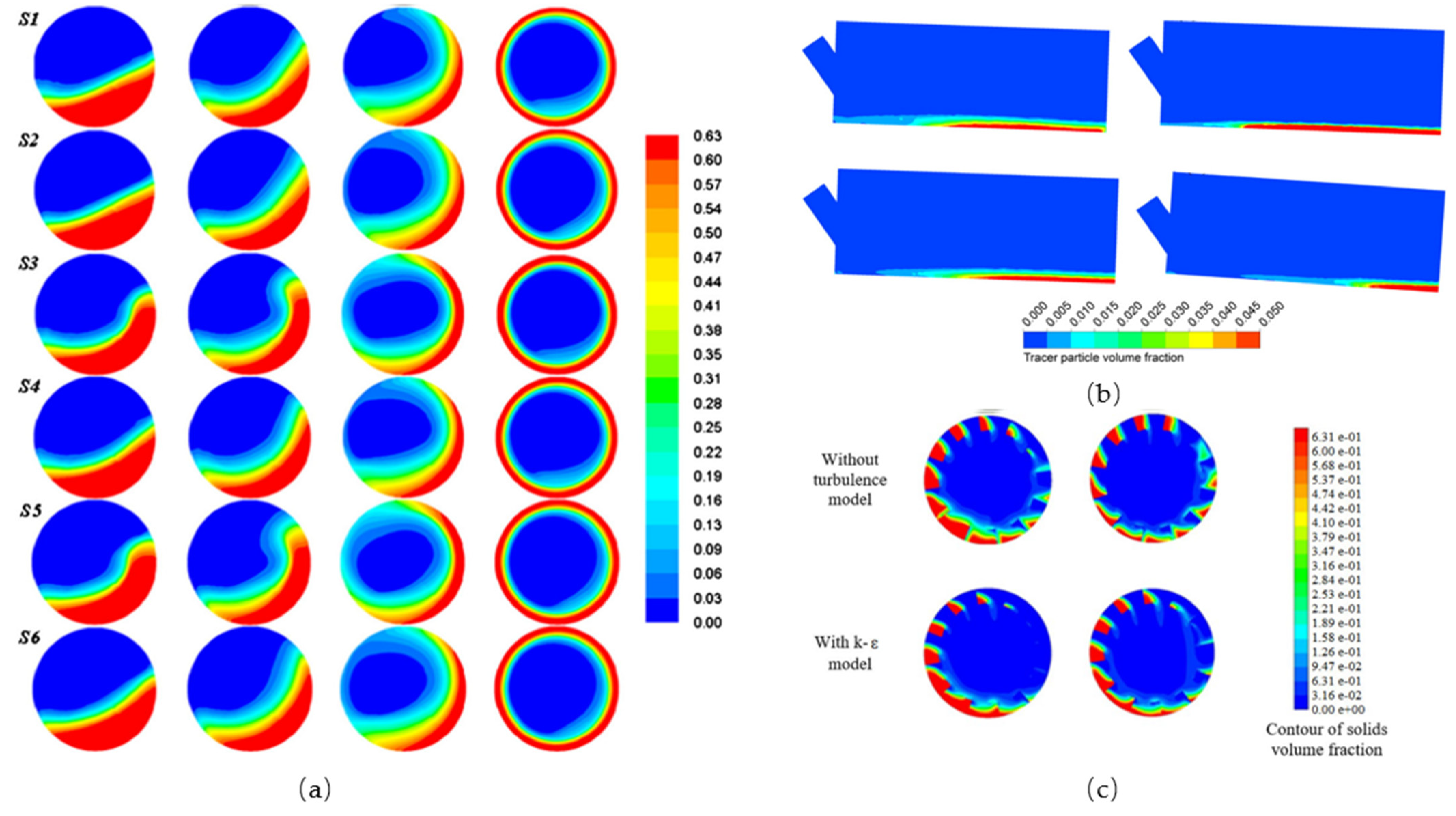
In order to simplify the simulation, uniform particles are assumed in most studies, even though they are rarely found in practice. Under this assumption, the model is verified by comparing it with laboratory-scale experiments in which uniform particles are used [21][18][10,50]. For the dense uniform particle flow in the rotating drum without flights, Demagh et al. [10][45] studied the particle flow characteristics in the two flow states of rolling and cascading, and found that the particle velocity direction on the particle bed surface is not always parallel to the bed surface, and there are included angles in some positions, indicating that the particles will not slide or roll, but jump when moving. Santos et al. [11][46] identified different regimes (rolling, cascading, cataracting and centrifuging) of solids in motion in a rotating drum. Furthermore, Delele et al. [13][42] used the model to study the effects of rotational speed, filling level, feed speed, and drum inclination angle on particle flow, and found that the particle flow near the surface of the particle bed has a strong entrainment effect on the transverse air flow. Similarly, the effects of rotational speed, restitution coefficient and particle size on the hydrodynamics of the particle was investigated by Taghizadeh et al. [18][50]. It is worth mentioning that the effects of these parameters on the granular temperature of particles was also studied. They found that the particle–particle restitution coefficient and rotational speed play a significant role in the granular temperature, and consequently on the hydrodynamic behavior of the bed. Moreover, the TFM-coupled KTGF and diverse heat transfer models were used to predict heat transfer in a rotating drum, and it was revealed that the bed surface velocity characteristic peak is located at the center and down the edges [14][47]. For the dense uniform particle flow in the rotating drum with flights, the configuration of flights plays an important role on the granular flow. The effects of the number of flights [20] [28], flight folding angle [20][28] and flight shape [15][17][22][27,49,52] on particle flow behavior were analyzed. The solid-hold-up in the flight was well predicted. Similar to the rotating drum without flights, the particle flow pattern, the effects of the operational parameters, the effects of the model parameters, and the heat transfer were also analyzed [12][16][17][17,48,49]. Moreover, Nascimento et al. [22][52] proposed for the first time that considering the turbulence effect in the model can better predict the active region and passive region of the particle bed. Figure 1 gives representative results.
Figure 1. (a) Volume fraction of the granular solid phase of 3.68 mm and fill level of 31.40% for drum rotating at 1.45, 4.08, 8.91 and 16.4 rad/s from the left to the right [11][46]; (b) axial distribution of the tracer particle volume fraction after an injection time of 60 s for different operating conditions of the drum [13][42]; (c) solid volume fraction distributions (passive phase) without and with the k-ε-turbulence model [22][52]. (Note: all the legends indicate volume fraction of particles).
It is about at spherical particles, while the flow process of uniform non-spherical particles in a rotating drum was studied by Benedito et al. [19][51]. It was found that by giving appropriate parameters, the model could be verified by comparing the rice grain velocities and the drum transverse plane with the experimental results. It is worth noting that this verification is accidental, because the parameters are given by the trial-and-error method instead of experimental measurement. In essence, the numerical model for non-spherical particles has not been developed.
2.3. Study on Mixing and Segregation of Dense Binary Particles
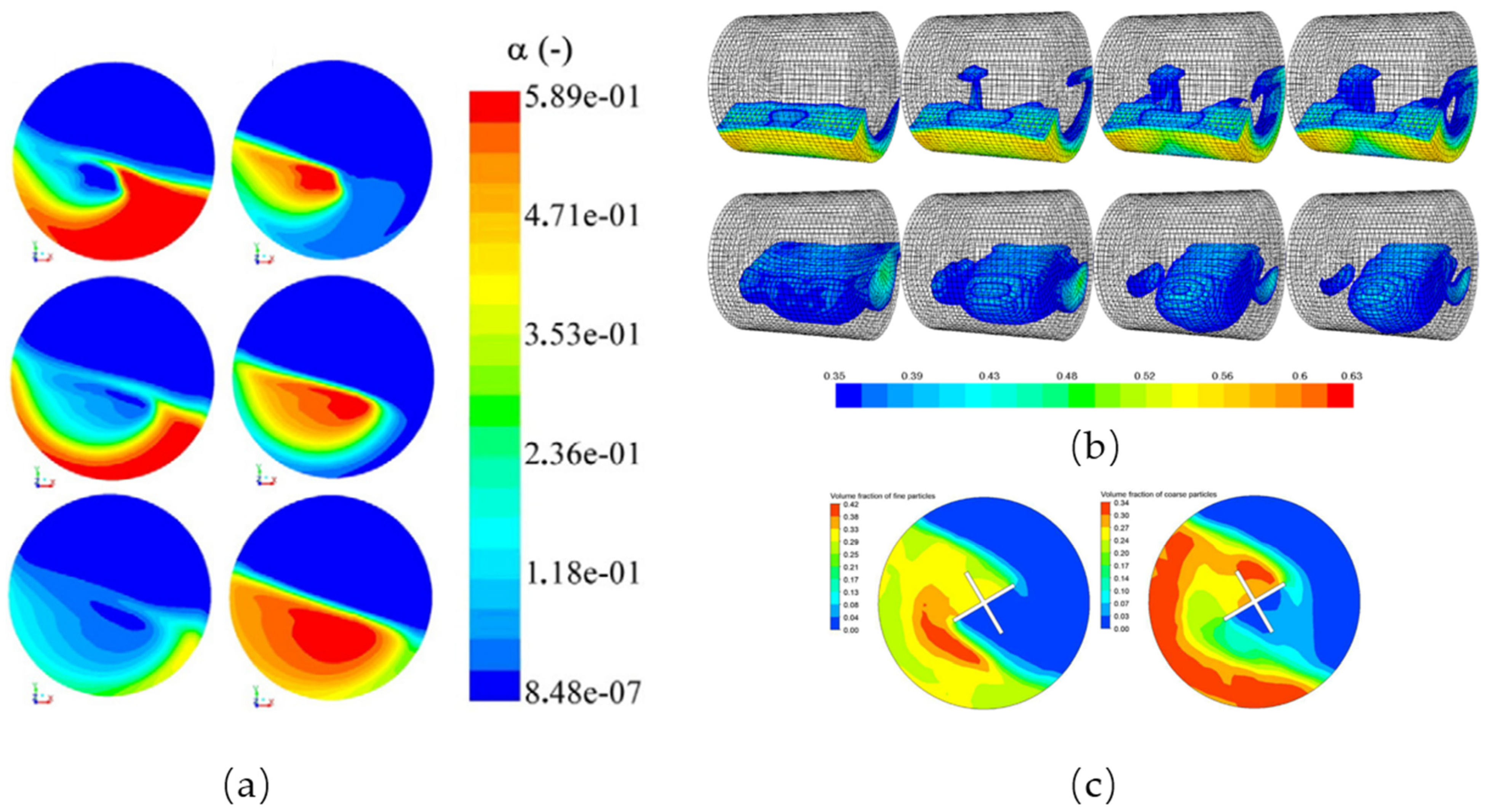
Compared with uniform particles in rotating drums, the mixing and segregation of binary particles occur due to different particle properties, which are more complex. There are generally two types of mixing in horizontal rotating drums: longitudinal and transverse. Similar to mixing, there are also two types of segregation: radial and axial segregation. He et al. [23] [15] first used the TFM coupled with KTGF to simulate binary particle segregation with different sizes in a rotating drum, which confirmed the predict applicability of the model. A clear core-shell structure in the transverse plane of the drum, in terms of the concentration of small and large particles, was predicted and an initial attempt was made to simulate the axial particle segregation. Santos et al. [25][53] conducted simulations to predict the mixing and segregation of particles in a rotating drum due to the different particle diameters. The predicted particle segregation was in good agreement with the experimental results. The internal structure of the bed material inside the drum which consisted of a symmetrical wing-shaped extension of small particles towards the drum end plates was observed. However, Huang et al. [24][29][32,54] observed that the TFM coupled with KTGF failed to predict the mixing and segregation of the particles in the rotating drum they investigated; then, they proposed the dynamic angle of repose fitting (DARF) and bed surface fitting (BSF) to modify the kinetic viscosity of the model. The results showed that the modified model was useful for analyzing the radial and axial segregation of particles in the rotating drum. Although these studies predict the typical mixing and segregation of particles using the model, the degree of particle mixing or segregation was not quantified. Referring to mixing indices in DEM simulation and experimental research, a mixing index based on sampling information from the computational grids was established [28][21]. The index was used for the quantitative analysis of the segregation degree of binary particles with different sizes in a rotating drum without a baffle, and drums with baffles of different shapes. It was found that the enhancement effect of the baffle on particle mixing was not obvious, and the mixing speed was too fast compared with the experimental results. Therefore, the TFM coupled with KTGF is applicable for predicting the mixing and segregation of binary particles in rotating drums, but the accuracy needs further discussion. The representative results are shown in Figure 2.
Figure 2. (a) Simulated drum transverse plane for the radial segregation analysis [25][53]; (b) the surface of the 0.775 mm solid phase (top row) and 0.385 mm solid phase (bottom row) [30][23]; (c) the mixing process of binary particles in the drum with “+” baffle [28][21]. (Note: all the legends indicate volume fraction of particles).
Table 1 summarizes the relevant studies including the representative model applications described above. It can be seen that TFM coupled with KTGF has been used for modeling dense granular flow in rotating drums since 2007. It has been used for only 14 years. Zhu et al. [7] has given a detailed review of DEM used for granular flow in rotating drums; it can be easily noticed that DEM has a longer history and has been more popular in this area than TFM. However, they indicated that the number of particles that can be dealt with at the moment is limited. Moreover, although there are model advantages of TFM compared with DEM, such as low computing resources and suitability for industrial-scale modeling, the model is still used for a laboratory-scale rotating drum (diameter less than 0.5 m), and no simulation for an industrial-scale rotating drum was found.
References
- Jaeger, H.M.; Nagel, S.R.; Behringer, R.P. The physics of granular materials. Phys. Today 1996, 49, 32–38. [Google Scholar] [CrossRef]Demagh, Y.; Ben Moussa, H.; Lachi, M.; Noui, S.; Bordja, L. Surface particle motions in rotating cylinders: Validation and similarity for an industrial scale kiln. Powder Technol. 2012, 224, 260–272.
- Dhakal, S. Experimental study of particle interactions in moderate to dense granular shear flows of disks. Condens. Matter 2017, 2, 2. [Google Scholar] [CrossRef]Santos, D.A.; Petri, I.J.; Duarte, C.R.; Barrozo, M.A.S. Experimental and CFD study of the hydrodynamic behavior in a rotating drum. Powder Technol. 2013, 250, 52–62.
- Atydu, T. Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1954, 225, 49–63. [Google Scholar] [CrossRef]Nascimento, S.M.; Santos, D.A.; Barrozo, M.A.S.; Duarte, C.R. Solids holdup in flighted rotating drums: An experimental and simulation study. Powder Technol. 2015, 280, 18–25.
- Yang, R.Y.; Zou, R.P.; Yu, A.B. Microdynamic analysis of particle flow in a horizontal rotating drum. Powder Technol. 2003, 130, 138–146. [Google Scholar] [CrossRef]Delele, M.A.; Weigler, F.; Franke, G.; Mellmann, J. Studying the solids and fluid flow behavior in rotary drums based on a multiphase CFD model. Powder Technol. 2016, 292, 260–271.
- Ottino, J.M.; Khakhar, D.V. Mixing and segregation of granular materials. Annu. Rev. Fluid Mech. 2000, 32, 55–91. [Google Scholar] [CrossRef]Liu, H.; Yin, H.; Zhang, M.; Xie, M.; Xi, X. Numerical simulation of particle motion and heat transfer in a rotary kiln. Powder Technol. 2016, 287, 239–247.
- Dhakal, S. Shear flow characteristics of densely packed granular material subjected to slow deformations. J. Nepal Geol. Soc. 2013, 46. [Google Scholar] [CrossRef]Machado, M.V.C.; Nascimento, S.M.; Duarte, C.R.; Barrozo, M.A.S. Boundary conditions effects on the particle dynamic flow in a rotary drum with a single flight. Powder Technol. 2017, 311, 341–349.
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: A review of major applications and findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]Machado, M.V.C.; Santos, D.A.; Barrozo, M.A.S.; Duarte, C.R. Experimental and Numerical Study of Grinding Media Flow in a Ball Mill. Chem. Eng. Technol. 2017, 40, 1835–1843.
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]Li, M.; Ling, X.; Peng, H.; Cao, Z.; Wang, Y. An investigation on heat transfer of granular materials in the novel flighted rotary drum. Can. J. Chem. Eng. 2017, 95, 386–397.
- Ingram, A.; Seville, J.P.K.; Parker, D.J.; Fan, X.; Forster, R.G. Axial and radial dispersion in rolling mode rotating drums. Powder Technol. 2005, 158, 76–91. [Google Scholar] [CrossRef]Taghizadeh, A.; Hashemabadi, S.H.; Yazdani, E.; Akbari, S. Numerical analysis of restitution coefficient, rotational speed and particle size effects on the hydrodynamics of particles in a rotating drum. Granul. Matter 2018, 20, 56.
- Demagh, Y.; Ben Moussa, H.; Lachi, M.; Noui, S.; Bordja, L. Surface particle motions in rotating cylinders: Validation and similarity for an industrial scale kiln. Powder Technol. 2012, 224, 260–272. [Google Scholar] [CrossRef]Benedito, W.M.; Duarte, C.R.; Barrozo, M.A.S.; dos Santos, D.A. An investigation of CFD simulations capability in treating non-spherical particle dynamics in a rotary drum. Powder Technol. 2018, 332, 171–177.
- Santos, D.A.; Petri, I.J.; Duarte, C.R.; Barrozo, M.A.S. Experimental and CFD study of the hydrodynamic behavior in a rotating drum. Powder Technol. 2013, 250, 52–62. [Google Scholar] [CrossRef]Nascimento, S.M.; Lima, R.M.; Brandão, R.J.; Duarte, C.R.; Barrozo, M.A.S. Eulerian study of flights discharge in a rotating drum. Can. J. Chem. Eng. 2019, 97, 477–484.
- Nascimento, S.M.; Santos, D.A.; Barrozo, M.A.S.; Duarte, C.R. Solids holdup in flighted rotating drums: An experimental and simulation study. Powder Technol. 2015, 280, 18–25. [Google Scholar] [CrossRef]Rong, W.; Feng, Y.; Schwarz, P.; Witt, P.; Li, B.; Song, T.; Zhou, J. Numerical study of the solid flow behavior in a rotating drum based on a multiphase CFD model accounting for solid frictional viscosity and wall friction. Powder Technol. 2020, 361, 87–98.
- Delele, M.A.; Weigler, F.; Franke, G.; Mellmann, J. Studying the solids and fluid flow behavior in rotary drums based on a multiphase CFD model. Powder Technol. 2016, 292, 260–271. [Google Scholar] [CrossRef]Nascimento, S.M.; Lima, R.M.; Brandão, R.J.; Santos, D.A.; Duarte, C.R.; Barrozo, M.A.S. Comparison between the Eulerian (CFD) and the Lagrangian (DEM) approaches in the simulation of a flighted rotary drum. Comput. Part. Mech. 2021, 1–13.
- Liu, H.; Yin, H.; Zhang, M.; Xie, M.; Xi, X. Numerical simulation of particle motion and heat transfer in a rotary kiln. Powder Technol. 2016, 287, 239–247. [Google Scholar] [CrossRef]He, Y.R.; Chen, H.S.; Ding, Y.L.; Lickiss, B. Solids motion and segregation of binary mixtures in a rotating drum mixer. Chem. Eng. Res. Des. 2007, 85, 963–973.
- Machado, M.V.C.; Nascimento, S.M.; Duarte, C.R.; Barrozo, M.A.S. Boundary conditions effects on the particle dynamic flow in a rotary drum with a single flight. Powder Technol. 2017, 311, 341–349. [Google Scholar] [CrossRef]Huang, A.N.; Kao, W.C.; Kuo, H.P. Numerical studies of particle segregation in a rotating drum based on Eulerian continuum approach. Adv. Powder Technol. 2013, 24, 364–372.
- Machado, M.V.C.; Santos, D.A.; Barrozo, M.A.S.; Duarte, C.R. Experimental and Numerical Study of Grinding Media Flow in a Ball Mill. Chem. Eng. Technol. 2017, 40, 1835–1843. [Google Scholar] [CrossRef]Santos, D.A.; Duarte, C.R.; Barrozo, M.A.S. Segregation phenomenon in a rotary drum: Experimental study and CFD simulation. Powder Technol. 2016, 294, 1–10.
- Li, M.; Ling, X.; Peng, H.; Cao, Z.; Wang, Y. An investigation on heat transfer of granular materials in the novel flighted rotary drum. Can. J. Chem. Eng. 2017, 95, 386–397. [Google Scholar] [CrossRef]Huang, A.N.; Kuo, H.P. CFD simulation of particle segregation in a rotating drum. Part I: Eulerian solid phase kinetic viscosity. Adv. Powder Technol. 2017, 28, 2094–2101.
- Taghizadeh, A.; Hashemabadi, S.H.; Yazdani, E.; Akbari, S. Numerical analysis of restitution coefficient, rotational speed and particle size effects on the hydrodynamics of particles in a rotating drum. Granul. Matter 2018, 20, 56. [Google Scholar] [CrossRef]Huang, A.N.; Kuo, H.P. CFD simulation of particle segregation in a rotating drum. Part II: Effects of specularity coefficient. Adv. Powder Technol. 2018, 29, 3368–3374.
- Benedito, W.M.; Duarte, C.R.; Barrozo, M.A.S.; dos Santos, D.A. An investigation of CFD simulations capability in treating non-spherical particle dynamics in a rotary drum. Powder Technol. 2018, 332, 171–177. [Google Scholar] [CrossRef]Rong, W.; Li, B.; Feng, Y.; Schwarz, P.; Witt, P.; Qi, F. Numerical analysis of size-induced particle segregation in rotating drums based on Eulerian continuum approach. Powder Technol. 2020, 376, 80–92.
- Nascimento, S.M.; Lima, R.M.; Brandão, R.J.; Duarte, C.R.; Barrozo, M.A.S. Eulerian study of flights discharge in a rotating drum. Can. J. Chem. Eng. 2019, 97, 477–484. [Google Scholar] [CrossRef]
- Rong, W.; Feng, Y.; Schwarz, P.; Witt, P.; Li, B.; Song, T.; Zhou, J. Numerical study of the solid flow behavior in a rotating drum based on a multiphase CFD model accounting for solid frictional viscosity and wall friction. Powder Technol. 2020, 361, 87–98. [Google Scholar] [CrossRef]
- Nascimento, S.M.; Lima, R.M.; Brandão, R.J.; Santos, D.A.; Duarte, C.R.; Barrozo, M.A.S. Comparison between the Eulerian (CFD) and the Lagrangian (DEM) approaches in the simulation of a flighted rotary drum. Comput. Part. Mech. 2021, 1–13. [Google Scholar] [CrossRef]
- He, Y.R.; Chen, H.S.; Ding, Y.L.; Lickiss, B. Solids motion and segregation of binary mixtures in a rotating drum mixer. Chem. Eng. Res. Des. 2007, 85, 963–973. [Google Scholar] [CrossRef]
- Huang, A.N.; Kao, W.C.; Kuo, H.P. Numerical studies of particle segregation in a rotating drum based on Eulerian continuum approach. Adv. Powder Technol. 2013, 24, 364–372. [Google Scholar] [CrossRef]
- Santos, D.A.; Duarte, C.R.; Barrozo, M.A.S. Segregation phenomenon in a rotary drum: Experimental study and CFD simulation. Powder Technol. 2016, 294, 1–10. [Google Scholar] [CrossRef]
- Huang, A.N.; Kuo, H.P. CFD simulation of particle segregation in a rotating drum. Part I: Eulerian solid phase kinetic viscosity. Adv. Powder Technol. 2017, 28, 2094–2101. [Google Scholar] [CrossRef]
- Huang, A.N.; Kuo, H.P. CFD simulation of particle segregation in a rotating drum. Part II: Effects of specularity coefficient. Adv. Powder Technol. 2018, 29, 3368–3374. [Google Scholar] [CrossRef]
- Rong, W.; Li, B.; Feng, Y.; Schwarz, P.; Witt, P.; Qi, F. Numerical analysis of size-induced particle segregation in rotating drums based on Eulerian continuum approach. Powder Technol. 2020, 376, 80–92. [Google Scholar] [CrossRef]
- Huang, A.N.; Liu, L.C.; Kuo, H.P. The role of end wall shearing in the drum segregation band formation. Powder Technol. 2013, 239, 98–104. [Google Scholar] [CrossRef]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of circulating fluidized beds: Kinetic theory approach. In Proceedings of the 7th Fluidization Conference, Gold Coast, Australia, 3–8 May 1992; pp. 75–82. [Google Scholar]
More
