Lattice Materials: Comparison
View Latest Version
Please note this is a comparison between Version 4 by Conner Chen and Version 3 by Conner Chen.

Lattice material is a cellular material consisting of a periodic network of structural elements such as rods or beams. This network of lattices exists over a wide spectrum of scale from the nanoscale to macroscale and has been applied in a wide area of applications. In the nanoscale spectrum, most of the CNT (Carbon Nano Tube) based sensors are made using lattice materials. Micro-lattices material is being developed intensively as it offers high energy absorption capability. On a macroscale, due to its high stiffness and lightweight properties, lattice materials are widely used in aerospace applications.

  • lattice materials
  • homogenization
  • topology optimization
  • computational
  • corrugated
  • structure
  • morphing
  • adaptive
  • 3D printing

1. Lattice Materials

Lattice material is a cellular material consisting of a periodic network of structural elements such as rods or beams. This network of lattices exists over a wide spectrum of scale from the nanoscale to macroscale and has been applied in a wide area of applications. In the nanoscale spectrum, most of the CNT (Carbon Nano Tube) based sensors are made using lattice materials [1] as shown in Figure 1a. Micro-lattices material is being developed intensively as it offers high energy absorption capability [2][3]. On a macroscale, due to its high stiffness and lightweight properties, lattice materials are widely used in aerospace applications [4][5][6][7][8].
Lattice structures or materials could be also classified into several parameters, namely, geometry, deformation properties, and rigidity. These determine a proper approach for understanding dynamics of lattice accurately extend to design. Geometry-based classification is widely received in mathematics and solid-state physics and especially in 2-D, two main categories are considered: regular and semi-regular [9]. Representatives of each group are illustrated in Figure 1. Sub-sequentially, three types exist under the regular lattice, namely, square lattice, triangular lattice, and hexagonal lattice. In semi-regular lattices, unit cells are tessellated Later, eight semi-regular lattices are introduced in this paper for more details [9].
Figure 1. Examples of different lattice topologies: (a) triangular; (b) Kagome; (c) diamond; (d) snub square [10].
In engineering applications, spatially periodic patterns of lattices can be viewed as a material or a structure depending on its length scale. When the deformation is at a much larger length scale than the individual beam length, such a network of a lattice is defined as “lattice material”. Figure 2  shows such an example of lattice materials. On the other hand, if the length scale between deformation and the individual beam is the same, then it is viewed as a “lattice structure”. Asymptotic Theory might be a more suitable approach when we are dealing with lattice materials [11]. Meanwhile, modeling the beam individually is a better approach for lattice structure. This paper will more focus on lattice materials rather than structure as it is more relevant to the homogenization method.
Materials 15 00605 g002 550
Figure 2. Lattice materials formed by network of beams; (a) ultralight Nano-metal truss hybrid lattice; (b) penta-mode lattice [12].
The other key parameter that determines a suitable approach for understanding lattices is relative density. The relative density is defined as the density ratio of lattice material to the solid material (ρ¯=ρ∗/ρs) and has a pivotal role in determining the elastostatic behavior of a lattice. Figure 3 shows the relationship between relative density and relative modulus. Slope 1 depicted in Figure 3 is for stretch-dominated lattice and slope 2 is for bending-dominated lattice. As it can be seen, honeycombs, one of the commonly used cores for sandwich panels, are extraordinarily efficient. Physically, relative density depicts the porosity of lattice material. A low value of relative density indicates high porosity, meanwhile, a high value of that indicates low porosity. For instance, ρ¯=1 means zero porosity as the density of the lattice is the same as one of the solid or bulk. Therefore, it is crucial to employ a proper homogenization model or approach according to the value of relative density. For the low value of relative density, e.g., ρ¯<0.3, applying Euler–Bernoulli beam or Timoshenko beam elements to model the cell-wall deformation will give an accurate result [13][14][15][16]. Furthermore, Micro-polar theory [17], Bloch Wave Analysis and Cauchy–Born hypothesis [18] might be employed for such cases as well. For a high value of relative density, the Asymptotic Homogenization method will give a better and more accurate result [11].
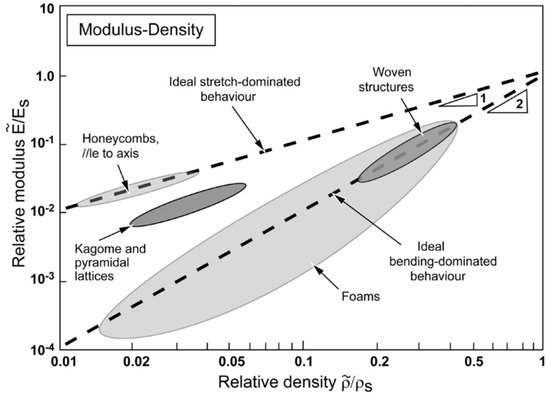
Materials 15 00605 g003 550
Figure 3. Relative modulus plotted against relative density on logarithmic scales for cellular structure [19].
Lattices can also be categorized into stretching-dominated or bending-dominated based on their rigidity [19]. Some representatives of both categories are shown in Figure 4. A bending-dominated lattice reacts to external loads by cell-wall bending due to its low nodal connectivity at the cell vertices. This results in a microscopic bending-dominated failure mode, where the cell elements collapse by bending stresses [18]. On the other hand, stretching-dominated lattices predominantly behave by stretching due to the high value of nodal connectivity at the cell vertices. For the same porosity or relative density, stretching-dominated lattices are stronger and have higher stiffness than bending-dominated lattices. Gibson and Ashby [20] performed structural analysis and found that the stiffness and the strength of lattice materials scale up with the value of relative density. The strength and stiffness of stretching-dominated lattice scale up linearly by its relative density (ρ¯), whereas the strength and stiffness of bending-dominated lattice are scaled up, respectively, by ρ¯2 and ρ¯1.5. For example, at ρ¯=0.01, the stretching-dominated lattice is far more superior than the bending-dominated lattice as it is 100 times stiffer and 10 times stronger.
Figure 4. (a) Bending dominated lattices (b) Stretching dominated lattices [11].

2. Analytical Research of Lattice Materials

For a periodic network of lattices to be considered as material, the characteristic length of its cells needs to be at least one or two orders of magnitude below the medium’s overall length scale. Hence, microscale study is vital to understand the full behavior of the structure at the global scale, which is the basic principle of the homogenization method. Numerous analytical and numerical methods have been constructed to determine the mechanical behavior of cellular materials [11][13][14][17][18][21][22][23][24][25]. All of these methods are based on various fields of physics and mathematics ranging from asymptotic theory [11], elasticity theory [13] to micro-polar theory [17]. Moreover, experimental work has been done as well [13][26][27] though it is limited in design complexity due to manufacturability in the process. However, recent advances in 3D manufacturing techniques such as 3D printing has significantly improved the production of lattice materials in terms of accuracy with various kind of solid materials. Nowadays the manufacturing process of lattice structure can be conducted at a very fine scale and with lower overall cost [28][29][30][31]. This advancement allows lattice materials to be more experimented on and be tested against existing numerical and analytical models [26][32].
The analytical works to analyze and develop a method to obtain mechanical behaviors and properties of cellular materials have been pioneered by several people; Gibson et al. [13], Masters et al. [16], Wang et al. [14], and Christensen [33]. They derived an analytical closed-form formula of mechanical properties of lattice materials for several shapes and geometry. Their method is based on one common ground assumption, which is that the cell behaves as Euler–Bernoulli beams. They obtain the mechanical properties by solving deformation and equilibrium problems for a single cell, which generates some limitations to the application of the analytical method. It could only be applied to a cell with a simple topology with small strains and no extreme change in geometry. Furthermore, it only works in lattice structures with small relative density value (ρ¯=0.3).
In terms of computational works, several different approaches have been developed. Asymptotic Homogenization (AH) has been extensively employed to obtain the mechanical properties of lattice materials [11][34][35]. AH has been proven and validated to be an effective homogenization method through comparisons with other methods and experimental verification [8]. As it does not have limits in the value of relative density. However, its major shortcoming is the computational cost. It is more expensive than other common approaches, especially when the problem contains a large number of variables [11][36]. Recently, a variational AH of beam-like square lattice structures has been discussed [34] and they explain and result when the microscale of the structure is in the finest scale, i.e., ϵ→0. Another computational approach is a matrix-based multiscale method introduced by Vigliotti et al. [24][37]. They performed a linear multiscale analysis and FEA (finite element analysis) on a stretching and bending-dominated lattice [37]. Furthermore, they have applied a method to develop a non-linear model for lattice materials [24].
Some homogenization approaches introduced here come from micro-polar theory [17][38][39][40] and solid-state physics [18][41]. The micro-polar theory introduces a microscopic rotation in addition to translational deformations. The micro-polar elastic constants of the stiffness matrix can be found through either analysis of the unit cell [17] or an energy approach [40]. From solid-state physics, the combination of Bloch’s theorem and the Cauchy–Born hypothesis has been applied to analyze mechanical behavior of planar lattices [18][41].
Recently, Machine Learning has been adopted to study lattice materials [36][42][43][44][45]. Koeppe et al. [36] have used a neural network on a set of simulation data to learn a parameterized mechanical model of a lattice structure with particular geometry. Mian et al. [42] obtained an elastic material model for lattice structure using both FEA (finite element analysis) and NN (Neural Network) approaches. These studies have produced results that are in good agreement with both experiment and simulation with a significant increase in computational time and prove that the data-driven method is an effective and efficient as well as reliable and accurate approach. In addition, Machine learning has been used to simulate anisotropic elastic-plastic behavior of cellular structure [45] and deep learning for topology optimization for lattice materials [44]. As machine learning and AI are developing in a rapid trend, data-driven methods are a rising prominent approach and worth looking into in the future of homogenization problems.

References

  1. Schroeder, V.; Savagatrup, S.; He, M.; Lin, S.; Swager, T.M. Carbon nanotube chemical sensors. Chem. Rev. 2019, 119, 599–663.
  2. Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28.
  3. Rashed, M.G.; Ashraf, M.; Mines, R.A.W.; Hazell, P.J. Metallic microlattice materials: A current state of the art on manufacturing, mechanical properties and applications. Mater. Des. 2016, 95, 518–533.
  4. Bici, M.; Brischetto, S.; Campana, F.; Ferro, C.G.; Seclì, C.; Varetti, S.; Maggiore, P.; Mazza, A. Development of a multifunctional panel for aerospace use through SLM additive manufacturing. Procedia CIRP 2018, 67, 215–220.
  5. Han, Y.; Wang, P.; Fan, H.; Sun, F.; Chen, L.; Fang, D. Free vibration of CFRC lattice-core sandwich cylinder with attached mass. Compos. Sci. Technol. 2015, 118, 226–235.
  6. Jenett, B.E.; Calisch, S.E.; Cellucci, D.; Cramer, N.; Gershenfeld, N.A.; Swei, S.; Cheung, K.C. Digital Morphing Wing: Active Wing Shaping Concept Using Composite Lattice-Based Cellular Structures. Soft Robot. 2017, 4, 33–48.
  7. Li, W.; Sun, F.; Wang, P.; Fan, H.; Fang, D. A novel carbon fiber reinforced lattice truss sandwich cylinder: Fabrication and experiments. Compos. Part A Appl. Sci. Manuf. 2016, 81, 313–322.
  8. Wei, K.; Peng, Y.; Qu, Z.; Zhou, H.; Pei, Y.; Fang, D. Lightweight composite lattice cylindrical shells with novel character of tailorable thermal expansion. Int. J. Mech. Sci. 2018, 137, 77–85.
  9. Cundy, H.M. Mathematical Models; Oxford University Press: Oxford, UK, 1956.
  10. Their, T.; St-Pierre, L. Stiffness and strength of a semi-regular lattice. Raken. Mek. 2017, 50, 137–140.
  11. Arabnejad, S.; Pasini, D. Mechanical properties of lattice materials via asymptotic homogenization and comparison with alternative homogenization methods. Int. J. Mech. Sci. 2013, 77, 249–262.
  12. Phani, A.S.; Hussein, M.I. Dynamics of Lattice Materials; Wiley Online Library: Hoboken, NJ, USA, 2017.
  13. Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. London. A Math. Phys. Sci. 1982, 382, 25–42.
  14. Wang, A.-J.; McDowell, D.L. In-Plane Stiffness and Yield Strength of Periodic Metal Honeycombs. J. Eng. Mater. Technol. 2004, 126, 137–156.
  15. Kelsey, S.; Gellatly, R.; Clark, B. The Shear Modulus of Foil Honeycomb Cores. Aircr. Eng. Aerosp. Technol. 1958, 30, 294–302.
  16. Masters, I.; Evans, K. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422.
  17. Wang, X.L.; Stronge, W.J. Micropolar theory for two–dimensional stresses in elastic honeycomb. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 2091–2116.
  18. Elsayed, M.S.; Pasini, D. Analysis of the elastostatic specific stiffness of 2D stretching-dominated lattice materials. Mech. Mater. 2010, 42, 709–725.
  19. Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30.
  20. Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999.
  21. Gonella, S.; Ruzzene, M. Homogenization and equivalent in-plane properties of two-dimensional periodic lattices. Int. J. Solids Struct. 2008, 45, 2897–2915.
  22. Rezakhani, R.; Cusatis, G. Generalized mathematical homogenization of the lattice discrete particle model. In Proceedings of the 8th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Toledo, Spain, 10–14 March 2013; pp. 261–271.
  23. Tollenaere, H.; Cailleire, D. Continuous Modelling of Lattice Structures by Homogenization. Dev. Comput. Aided Des. Model. Civ. Eng. 2009, 29, 699–705.
  24. Vigliotti, A.; Deshpande, V.S.; Pasini, D. Non linear constitutive models for lattice materials. J. Mech. Phys. Solids 2014, 64, 44–60.
  25. Wang, A.-J.; McDowell, D. Yield surfaces of various periodic metal honeycombs at intermediate relative density. Int. J. Plast. 2005, 21, 285–320.
  26. Park, S.-I.; Rosen, D.W.; Choi, S.-K.; Duty, C.E. Effective Mechanical Properties of Lattice Material Fabricated by Material Extrusion Additive Manufacturing. Addit. Manuf. 2014, 1, 12–23.
  27. Salehian, A.; Inman, D.J. Dynamic analysis of a lattice structure by homogenization: Experimental validation. J. Sound Vib. 2008, 316, 180–197.
  28. Du, Y.; Gu, D.; Xi, L.; Dai, D.; Gao, T.; Zhu, J.; Ma, C. Laser additive manufacturing of bio-inspired lattice structure: Forming quality, microstructure and energy absorption behavior. Mater. Sci. Eng. A 2020, 773, 138857.
  29. Rehme, O.; Emmelmann, C. Rapid manufacturing of lattice structures with selective laser melting. In Laser-Based Micropackaging; International Society for Optics and Photonics: San Jose, CA, USA, 2006; Volume 6107, p. 61070K.
  30. Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 325–332.
  31. Tran, H.T.; Chen, Q.; Mohan, J.; To, A.C. A new method for predicting cracking at the interface between solid and lattice support during laser powder bed fusion additive manufacturing. Addit. Manuf. 2020, 32, 101050.
  32. Cheng, L.; Liang, X.; Belski, E.; Wang, X.; Sietins, J.M.; Ludwick, S.; To, A.C. Natural Frequency Optimization of Variable-Density Additive Manufactured Lattice Structure: Theory and Experimental Validation. J. Manuf. Sci. Eng. 2018, 140.
  33. Christensen, R. Mechanics of cellular and other low-density materials. Int. J. Solids Struct. 2000, 37, 93–104.
  34. Barchiesi, E.; Khakalo, S. Variational asymptotic homogenization of beam-like square lattice structures. Math. Mech. Solids 2019, 24, 3295–3318.
  35. Hassani, B.; Hinton, E. A review of homogenization and topology optimization I—homogenization theory for media with periodic structure. Comput. Struct. 1998, 69, 707–717.
  36. Koeppe, A.; Padilla, C.A.H.; Voshage, M.; Schleifenbaum, J.H.; Markert, B. Efficient numerical modeling of 3D-printed lattice-cell structures using neural networks. Manuf. Lett. 2018, 15, 147–150.
  37. Vigliotti, A.; Pasini, D. Linear multiscale analysis and finite element validation of stretching and bending dominated lattice materials. Mech. Mater. 2012, 46, 57–68.
  38. Askar, A.; Cakmak, A. A structural model of a micropolar continuum. Int. J. Eng. Sci. 1968, 6, 583–589.
  39. Chen, Y.; Liu, X.N.; Hu, G.K.; Sun, Q.; Zheng, Q.S. Micropolar continuum modelling of bi-dimensional tetrachiral lattices. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20130734.
  40. Kumar, R.S.; McDowell, D.L. Generalized continuum modeling of 2-D periodic cellular solids. Int. J. Solids Struct. 2004, 41, 7399–7422.
  41. Chiras, S.; Mumm, D.; Evans, A.; Wicks, N.; Hutchinson, J.; Dharmasena, K.; Wadley, H.; Fichter, S. The structural performance of near-optimized truss core panels. Int. J. Solids Struct. 2002, 39, 4093–4115.
  42. Alwattar, T.A.; Mian, A. Development of an Elastic Material Model for BCC Lattice Cell Structures Using Finite Element Analysis and Neural Networks Approaches. J. Compos. Sci. 2019, 3, 33.
  43. Arbabi, H.; Bunder, J.E.; Samaey, G.; Roberts, A.J.; Kevrekidis, I.G. Linking Machine Learning with Multiscale Numerics: Data-Driven Discovery of Homogenized Equations. JOM 2020, 72, 4444–4457.
  44. Kollmann, H.T.; Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Deep learning for topology optimization of 2D metamaterials. Mater. Des. 2020, 196, 109098.
  45. Settgast, C.; Hütter, G.; Kuna, M.; Abendroth, M. A hybrid approach to simulate the homogenized irreversible elastic–plastic deformations and damage of foams by neural networks. Int. J. Plast. 2020, 126, 102624.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback