A reactive power compensation method: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Conner Chen and Version 1 by Dariusz Zieliński.

One of the main challenges of today’s electrical power engineering is the symmetrization of grid voltages and the minimization of reactive power flows in distribution networks. There are many negative effects associated with asymmetry in power systems, such as increased losses in electric motors, harmonics transferred to DC systems, or phase currents inequality.

  • microgrid
  • reactive power compensation

1. Introduction

One of the main challenges of today’s electrical power engineering is the symmetrization of grid voltages and minimization of reactive power flows in distribution networks. There are many negative effects associated with asymmetry in power systems, such as increased losses in electric motors, harmonics transferred to DC systems, or phase currents inequality [1]. The research on four-wire converters and voltage asymmetry compensation methods in the distribution networks has already been carried out. The solution presented in [2] describes the control method for inverters, which is characterized by resistive behavior for grid disturbances. Voltage distortions are also inextricably linked with the load unbalances. There are proposals of load compensation under distorted voltages that are based on instantaneous symmetrical component theory with positive sequence extraction [3] or differentially rotating reference frame systems [4]. Other approaches are connected with neutral current compensation [5,6][5][6] and fuzzy neural networks [7]. However, the problem that has not been addressed in the research publications is the correlation between the asymmetry of phase angles and the reactive power compensators output power factor. It should be emphasized that non-linear and asymmetric loading of distribution networks [8,9][8][9] causes significant voltage asymmetry but also the phase angle shift. This problem is exacerbated in the systems where the short-circuit impedance is high—we can definitely include microgrids among them [10,11][10][11]. For the aforementioned reason, it is required to develop methods of controlling active and reactive power in the microgrid asymmetry states, which will be immune to the angular asymmetry between voltage vectors.
The low voltage distribution system is characterized by the fact that a large number of receivers with various characteristics are connected to it [12]. Most of the devices connected to the grid are single-phase loads. An increasing number of them have power systems which are based on electronic converters [13]. The use of this technology results from the requirements regarding their dimensions, weight, and price. The major problem arising from the use of such converters is the fact that they consume current in a non-linear manner [14]. An additional problem is the reactive power demand. Due to the presented factors, the parameters of the power grid deteriorate [15,16][15][16]. Phase-to-phase asymmetry appears, the voltage total harmonic distortion (THD) in the grid increases, and the increasing amount of reactive power reduces the grid capacity and causes voltage drops. The parameter that also changes is the phase angle between the voltage vectors. The measurements in the low voltage networks with a large number of consumers show that the phase angles are not symmetrical. Figure 1 and Figure 2 show the measurements made using Kyoritsu KEW6310 (Kyoritsu, Tokyo, Japan), which is power quality analyzer.
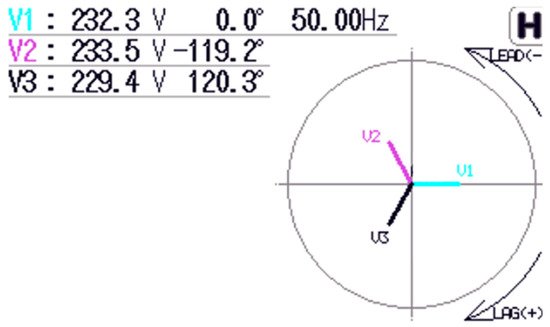
Energies 15 00497 g001 550
Figure 1. The angular asymmetry between voltage vectors: reference grid measurement.
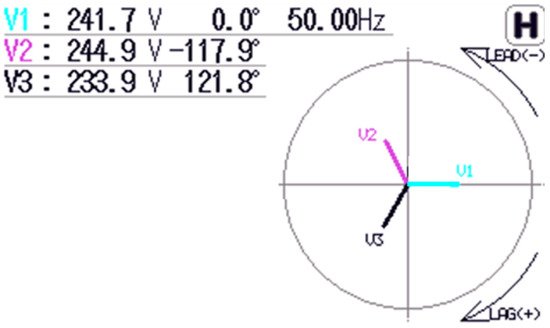
Energies 15 00497 g002 550
Figure 2. The angular asymmetry between voltage vectors: microgrid measurement.
Subsequent measurements were made in the microgrid, where one of the phases was heavily loaded. The angular error has been observed to become worse. The voltage asymmetry between phase 2 and phase 3 is 11 V. The results are presented Figure 2.
The angular asymmetry between voltage vectors has a significant impact on the operation of three-phase systems containing transformers, motors, and power converters. This article discusses the problem of reactive power compensation in a microgrid by a three-phase converter in the presence of angular errors. The microgrid system was selected as the research object due to high impact of its parameter fluctuations on the stability and efficiency of the entire system. A four-wire three-level AC/DC converter was used to solve the presented problem. This solution can be implemented particularly in radial grids and non-urban areas as a device maintaining the parameters of the electrical grid.

2. Phase-Independent Reactive Power Compensation with the Use of Four-Wire Hybrid Converter with Proportional-Resonant Regulators

The microgrids are characterized by the fact that their structure includes devices which are working as the current sources. These are generators based on internal combustion engines, electrochemical or mechanical energy storages, and renewable energy sources. All these devices are connected with each other by converters that synchronize with the grid. A typical structure of such a system is shown in Figure 3.
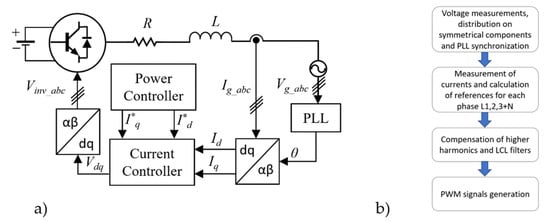
Energies 15 00497 g003 550
Figure 3. (a) Typical control structure of a converter integrated with renewable energy sources. (b) The flowchart of the multi-resonant algorithm. I*q, I*d—Reference current value in dq frame; Id, Iq—feedback currents after Park transform; Vdq—voltage signals in dq frame; Ig_abc, Vg_abc—Three phase instantaneous currents and voltages. Vinv_abc—three phase reference signals for PWM module.
The three-phase converter system for renewable energy sources presented in Figure 3 uses PLL (Phase-locked Loop) systems for synchronization with the grid [17,18,19][17][18][19]. These systems can be divided into those with a system of decomposition into symmetrical components and without this functionality. A common feature of these systems is the generation of a sawtooth signal common to three phases, which maps the actual vector angle of the grid voltage. Unfortunately, the PLL systems used in microgrid-connected three-phase converters do not meet the proper synchronization requirements connected with the angular asymmetry between the individual phases. When this asymmetry is not detected, the unwanted amounts of power will be drawn or delivered by the converters connected to the microgrid system. It should be emphasized that the microgrids are loaded asymmetrically. As a result, the value of active and reactive power is different in each of the phases. Therefore, the developed reactive power compensator should provide phase-independent reactive power compensation in the presence of angular asymmetry between voltage vectors. This type of operation can be achieved by replacing the classical synchronization and power calculation system based on the classical theory of instantaneous power with a solution that takes into account the phase angles of individual phases. The system is complemented by the use of a converter system that enables independent power control for each of the phases, despite the presence of disturbances in the microgrid parameters. The flowchart of the multi-resonant algorithm is presented in Figure 3a.
The proposed solution is a four-wire AC/DC converter (Figure 4). Its construction is based on a three-level T-type topology [20,21,22][20][21][22]. The fourth branch acts as a neutral wire and it enables phase-independent reactive power compensation. This solution is realized by a serial connection of Cx1 and Cx2 capacitors. As a result, the DC bus voltage is split in two. The application of increased capacity on the DC bus improves the operation of the system in dynamic states. In this context, the use of supercapacitors may be considered [23,24][23][24]. LN inductance is connected between neutral point and Q13–Q14 transistors. This connection allows for the active voltage stabilization on split DC bus. The inductive-capacitive-inductive (LCL) filter is used at the output of the converter, tuned to eliminate interference from the switching transistors.
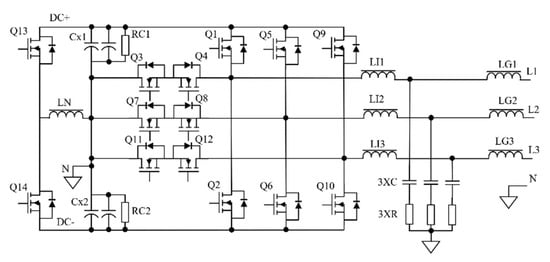
Energies 15 00497 g004 550
Figure 4. Hybrid converter in a three-phase, three-level four-wire configuration to enable the phase-independent reactive power compensation.
Due to the fact that each phase of the converter is controlled independently, the control system was considered as single-phase for further analysis. Subsequently, the system was expanded to three phases during simulation studies.
The main problem which is not mentioned by literature is the proper synchronization with unbalanced phase angles and correct calculation of the converter output currents value. The basic method uses a three-phase synchronous reference frame phase-locked loop (SRF-PLL) [25,26][25][26]. The synchronization method generates a sawtooth signal θ, which carries a phase angle value in the range from 0 to 2π.
The synchronization angle θ is used for the calculation of active and reactive current values in the dq frame. This calculation is realized in two steps: The first one is to pass the current signal through the Second-Order Generalized Integrator filter (SOGI), which shifts the measured phase by 90 degrees [27,28][27][28]. The second one is the active and reactive current components generation via the Park transform, which is based on the previously calculated signal by the PLL and phase current signal.
[ d q 0 ] = 2 3 [ cos ( θ ) sin ( θ ) 0 − sin ( θ ) cos ( θ ) 0 0 0 1 ] × [ α β ]
The method presented in Figure 5a is simple and efficient but causes current calculation errors if the voltage vectors of the weak utility grid are no longer shifted by 120 degrees. Figure 6 presents the value of dq signals as a function of the synchronization angle. The solution that will overcome these errors is presented in Figure 5b. Instead of a calculation of three 120 degree-shifted signals by a single PLL, three separate PLLs are used to calculate the correct angle of the voltage in each phase independently. In this case, the problem presented in Figure 6 no longer exists: the calculated currents are the base of the active and reactive current control loop.
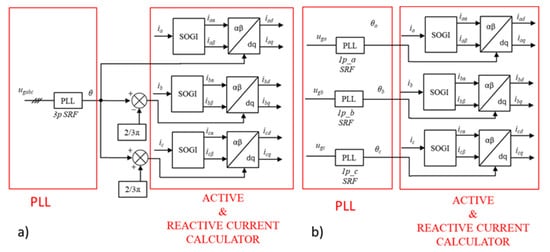
Energies 15 00497 g005 550
Figure 5. The method of active and reactive power calculation. (a) System with standard three phase-based PLL signal. (b) System with three individual PLL signals, which is the proposed method for the presence of angular asymmetry between voltage vectors.
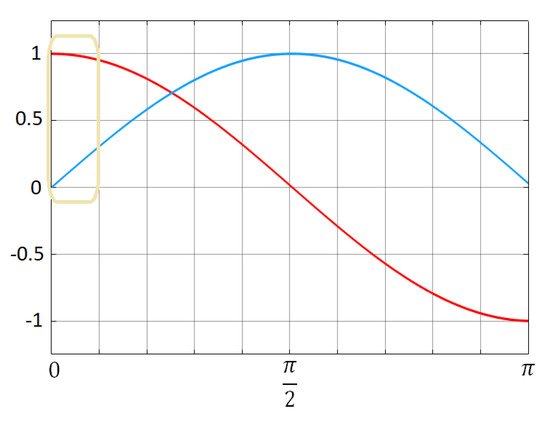
Energies 15 00497 g006 550
Figure 6. The changes of d and q components on the Park transform output as a function of phase angle.

References

  1. Awad, F.H.; Mansour, A.A.; Marei, M.I.; Sattar, A.A. Compensation the Unbalance of Non-Linear Load Based on Three-Leg Center-Split Inverter Four Wire. In Proceedings of the 6th International Conference on Advanced Control Circuits and Systems (ACCS) & 5th International Conference on New Paradigms in Electronics & information Technology (PEIT), Hurgada, Egypt, 17–20 November 2019; pp. 229–236.
  2. Meersman, B.; Renders, B.; Degroote, L.; Vandoorn, T.; Vandevelde, L. Control design of grid-connected three-phase inverters for voltage unbalance correction. In Proceedings of the 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK, 1–4 September 2009; pp. 1–5.
  3. Mishra, M.K.; Ghosh, A.A.; Joshi, A.; Suryawanshi, H.M. A Novel Method of Load Compensation under Unbalanced and Distorted Voltages. IEEE Trans. Power Deliv. 2007, 22, 288–295.
  4. Vechium, I.; Camblong, H.; Tapia, G.; Curea, O.; Dakyo, B. Modelling and control of four-wire voltage source inverter under unbalanced voltage condition for hybrid power system applications. In Proceedings of the European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005; p. 10.
  5. Tan, K.-H.; Lin, F.-J.; Chen, J.-H. A Three-Phase Four-Leg Inverter-Based Active Power Filter for Unbalanced Current Compensation Using a Petri Probabilistic Fuzzy Neural Network. Energies 2017, 10, 2005.
  6. Ning-Yi, D.; Wong, M.C.; Han, Y.D. Application of a three-level NPC inverter as a three-phase four-wire power quality compensator by generalized 3DSVM. IEEE Trans. Power Electron. 2006, 21, 440–449.
  7. Saber, B.; Abdelkader, B.; Said, B.; Mansour, B.B. Neutral Current Compensation of Three-Phase Four-wire Distribution System Using Three-Level Four-Leg DSTATCOM Based on Simplified 3DSVM Algorithm. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 1–6.
  8. Krishna, T.N.V.; Sathishkumar, P.; Himasree, P.; Punnoose, D.; Raghavendra, K.V.G.; Himanshu; Naresh, B.; Rana, R.A.; Kim, H.-J. 4T Analog MOS Control-High Voltage High Frequency (HVHF) Plasma Switching Power Supply for Water Purification in Industrial Applications. Electronics 2018, 7, 245.
  9. Krishna, T.N.V.; Himasree, P.; Rao, S.S.; Kumar, Y.A.; Kundakarla, N.B.; Kim, H.J. Design and Development of a Digital Controlled Dielectric Barrier Discharge (DBD) AC Power Supply for Ozone Generation. J. Sci. Ind. Res. 2020, 79, 1057.
  10. Narayanan, N.; Shan, S.; Umanand, L. Stability Analysis of Phase Locked Loop Controllers for Grid Tied Inverters in Weak Microgrids. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–5.
  11. Adib, A.; Mirafzal, B.B.; Wang, X.; Blaabjerg, F. On Stability of Voltage Source Inverters in Weak Grids. IEEE Access 2018, 6, 4427–4439.
  12. Dickert, J.; Domagk, M.; Schegner, P. Benchmark low voltage distribution networks based on cluster analysis of actual grid properties. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6.
  13. Kaipia, T.; Peltoniemi, P.; Lassila, J.; Salonen, P.; Partanen, J. Impact of low voltage DC system on reliability of electricity distribution. In Proceedings of the 20th International Conference and Exhibition on Electricity Distribution CIRED—Part 1, Prague, Czech Republic, 8–11 June 2009; pp. 1–4.
  14. Darbali-Zamora, R.; Ortiz-Rivera, E.I. An Overview into the Effects of Nonlinear Phenomena in Power Electronic Converters for Photovoltaic Applications. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019; pp. 2908–2915.
  15. Albana, I. Effects of the Reactive Power Injection on the Grid—The Rise of the Volt/var Interaction Chain. Smart Grid Renew. Energy 2016, 7, 217–232.
  16. Islam, M.; Mithulananthan, N.; Hossain, J.; Shah, R. Dynamic voltage stability of unbalanced distribution system with high penetration of single-phase PV units. In Proceedings of the The 9th International Conference on Power Electronics, Machines and Drives (PEMD 2018), Liverpool, UK, 17–19 April 2018; pp. 4074–4080.
  17. Zieliński, D.; Lipnicki, P.; Jarzyna, W. Synchronization of voltage frequency converters with the grid in the presence of notching. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2015, 34, 657–673.
  18. Peña Asensio, A.; Gonzalez-Longatt, F.; Arnaltes, S.; Rodríguez-Amenedo, J.L. Analysis of the Converter Synchronizing Method for the Contribution of Battery Energy Storage Systems to Inertia Emulation. Energies 2020, 13, 1478.
  19. Rizqiawan, A.; Hadi, P.; Fujita, G. Development of Grid-Connected Inverter Experiment Modules for Microgrid Learning. Energies 2019, 12, 476.
  20. Zhang, L.; Shi, D.; Jiang, W.; Yang, T.; Jin, C.; Zhang, Y.; Loh, W.K.; Tang, Y. Three-Phase-Four-Wire Three-Level Inverter with Neutral Inductor and Neutral Module for Saving AC-Filter-Inductances and DC-Link-Capacitances. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5656–5661.
  21. Peng, H.; Yuan, Z.; Woldegiorgis, D.L.; Emon, A.I.; Narayanasamy, B.; Liu, Y.; Luo, F.; Mantooth, A.; Mhiesan, H.G. Practical Design and Evaluation of a High-Efficiency 30-kVA Grid-Connected PV Inverter with Hybrid Switch Structure. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3670–3676.
  22. Yuan, Z.; Deshpande, A.; Narayanasamy, B.; Peng, H.; Emon, A.I.; Whitt, R.; Nafis, B.M.; Luo, F.; Huitink, D. Design and Evaluation of A 150 kVA SiC MOSFET Based Three Level TNPC Phase-leg PEBB for Aircraft Motor Driving Application. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6569–6574.
  23. Kumar, Y.A.; Kim, H.-J. Effect of Time on a Hierarchical Corn Skeleton-Like Composite of as Capacitive Electrode Material for High Specific Performance Supercapacitors. Energies 2018, 11, 3285.
  24. Yedluri, A.K.; Anitha, T.; Kim, H.-J. Fabrication of Hierarchical NiMoO4/NiMoO4 Nanoflowers on Highly Conductive Flexible Nickel Foam Substrate as a Capacitive Electrode Material for Supercapacitors with Enhanced Electrochemical Performance. Energies 2019, 12, 1143.
  25. Rodriguez, P.; Pou, J.; Bergras, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. De-coupled double synchronous reference frame PLL for power converters control. IEEE Trans. Power Electron. 2007, 22, 584–592.
  26. Jarzyna, W.; Zieliński, D.; Gopakumar, K. An evaluation of the accuracy of in-verter sync angle during the grid’s disturbances. Metrol. Meas. Syst. 2020, 27, 355–371.
  27. Jarzyna, W. A survey of the synchronization process of synchronous generators and power electronic converters. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 67,1069–1083.
  28. Nicastri, A.; Nagliero, A. Comparison and evaluation of the PLL techniques for the design of the grid-connected inverter systems. In Proceedings of the IEEE International Symposium on Indus-trial Electronics, Bari, Italy, 4–7 July 2010; pp. 3865–3870.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback