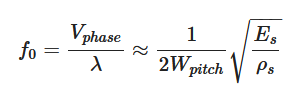Piezoelectric MEMS Laterally Vibrating Resonators (LVRs), which belong to one type of micromachined resonators that uses piezoelectric transduction, are characterized by dominant mechanical vibration in the lateral direction (within the plane of the device). In piezoelectric MEMS LVRs, the electric field is mainly applied across the thickness of the piezoelectric film to generate a lateral strain within the plane of the device with suspended free edges. Due to the lithographically definable resonant frequency, piezoelectric LVRs feature wide operation frequency coverage (from tens of MHz to several GHz) and provide a pathway towards realizing a multi-frequency integrated solution on a single chip. Depending on the structure of resonators, piezoelectric MEMS LVRs can be categorized into two types. The first type of LVRs consists of a piezoelectric film, both as the transducer and acoustic cavity. The second type of LVRs uses the thin piezoelectric film as a transducer only while having most of the acoustic energy propagating in the underlying thicker substrate. Such resonators are usually referred to as thin-film piezoelectric-on-substrate (TPoS) resonators. Typical applications of piezoelectric MEMS LVRs include resonant sensors, oscillators and RF filters.
- piezoelectric
- mems
- resonators
- laterally vibrating
- TPoS
- quality factor
- energy dissipation
- resonant sensors
- RF filters
1. Introduction
Resonant sensors, characterized by a resonant frequency dependent on the physical measurand, offer a great advantage over conventional analog sensors in that a frequency outputs can be digitized through mature frequency counting techniques realizable in digital systems [1]. This greatly reduces the complexity and cost generally associated with using the analog-to-digital converters to measure the amplitude of analogue voltages. As the information of the measurand is carried by frequency instead of amplitude, resonant sensors usually exhibit better immunity to interference or noise compared to their analog counterparts [2]. One of the widely-used resonant sensors is the quartz crystal microbalance (QCM), the operation of which relies on direct and inverse piezoelectric effects inherent to quartz resonators [3]. Although QCMs have high Q, large power handling capability and excellent temperature stability for certain cut angles, miniaturization of quartz resonators is still very challenging, which makes it difficult to integrate the quartz resonators monolithically with integrated circuits (IC) [4]. With the rapid development of micro-fabrication techniques, resonant sensors based on various micromachined piezoelectric resonators, such as thin film bulk acoustic wave resonators (FBARs) [5][6][7][5,6,7], laterally vibrating resonators (LVRs) [8][9][10][11][8,9,10,11] and flexural-mode beam resonators [12][13][14][12,13,14], have been proposed with fabrication processes compatible with mainstream IC technologies. For FBARs and flexural-mode beam resonators, the sensitivity per unit area and resonant frequency are both dependent on the thickness of resonant structures, which makes it hard to decouple these two important design parameters [15]. Moreover, FBARs normally have resonant frequencies in the GHz range due to difficulty in depositing thick piezoelectric films with good quality. It should be noted that a higher operating frequency of a resonant sensor does not necessarily translate into improved overall sensor performance as the noise level usually deteriorates with frequency, and it is generally accepted that higher operating frequency results in larger power consumption and design complexity for the read-out electronic circuit [15]. In contrast to FBARs and flexural beam resonators, LVRs feature lithographically definable resonant frequencies that are independent of thickness. Therefore, the sensitivity of resonant sensors based on LVRs can be improved by reducing the thickness while keeping resonant frequencies unchanged, unlike FBARs. This unique characteristic, combined with compatible manufacturing process with ICs, has rendered LVR a viable candidate for future integrated resonant sensors with miniaturized dimensions, high performance and low power consumption. Over the last two decades, a significant number of high-performance resonant sensors based on LVRs have been demonstrated, such as chemical sensors [16][17][16,17], thermal detectors [9][18][9,18], infrared sensors [19], biological sensors [20][21][20,21], inertial sensors [22][23][22,23], magnetometers [24][25][24,25] and miniaturized acoustic antennas [26].
In piezoelectric MEMS LVRs, the electric field is mainly applied across the thickness of the piezoelectric film to generate a lateral strain within the plane of the device with suspended free edges. The amplitude of lateral vibration becomes maximum when the frequency of the excitation signal coincides with the mechanical resonance of the resonator. For further details on the working principle of piezoelectric LVRs, we refer readers to references [15][27][15,27]. There are two types of electrode configurations that are commonly adopted for LVRs. The first type uses interdigital transducer (IDT) electrodes only on one side of piezoelectric film [28][29][28,29], while the second type has top and bottom electrodes on both sides of piezoelectric film [30][31][30,31]. Depending on the structure of resonators, piezoelectric MEMS LVRs can also be categorized into two types. The first type of LVRs consists of a piezoelectric film, both as the transducer and acoustic cavity [32]. The commonly-used piezoelectric materials include aluminum nitride (AlN) [32], lithium niobate (LN) [28], zinc oxide (ZnO) [27], gallium nitride (GaN) [33] and lead zirconate titanate (PZT) [34]. The second type of LVRs uses the thin piezoelectric film as a transducer only while having most of the acoustic energy propagating in the underlying thicker substrate [27]. Such resonators are usually referred to as thin-film piezoelectric-on-substrate (TPoS) resonators. Compared to the LVRs using only the piezoelectric film as the resonator body, TPoS LVRs generally exhibit higher Q and larger power handling capability when appropriate substrate materials are adopted. The commonly-used substrate materials include silicon [35], diamond [36] and silicon carbide [37]. As a trade-off, the effective electromechanical coupling (keff2) of TPoS LVRs is usually lower than piezoelectric-only LVRs as a significant part of the electrical energy transformed into acoustic energy is stored in the substrate layer. To improve the keff2 of TPoS, a novel type of sidewall-excited LVRs has been reported as a potential solution [38].
Figure 1a shows a typical structure of a TPoS resonator, which consists of input/output IDT electrodes, piezoelectric film, bottom electrode and substrate layer. When Si is used as the substrate layer, a bottom electrode layer could be omitted by highly doping the top surface of Si substrate and let it serve as the “bottom electrode” [39]. The applied AC electric field across the thickness of the piezoelectric film (denoted as z direction) causes it to expand and contract in the y direction through the piezoelectric coefficient d31. Figure 1b,c depicts the perspective and cross-sectional views of the indented fundamental symmetrical (S0) mode of Lamb wave. It should be noted that the electromechanical transduction efficiency is maximized when the electric field and strain field in the piezoelectric film are matched. That is to say, the indented S0 mode can be efficiently excited when the center-to-center pitch of the electrodes equals to half wavelength (λ) of the Lamb wave as shown in Figure 1c. As such, the resonant frequency of the LVR is given by:
where Vphase denotes the acoustic phase velocity of the resonator. Es and ρs are the Young’s modulus and mass density of the substrate layer, respectively. It should be noted that Equation (1) approximates the acoustic phase velocity using only the material properties of the substrate layer, which is usually much thicker than the other constituent layers of TPoS LVRs. Equation (1) indicates a key feature of LVRs, which is that the resonant frequency of the device can be set by the lithographically defined dimension. Although Equation (1) uses variable “Wpitch” for the case where IDT electrodes are adopted, one can simply replace Wpitch with other physical dimensions that represent half of acoustic wavelength in LVRs using patch electrodes (e.g., the width of the resonator in the width-extensional LVRs [39]). Figure 1d shows the electrical characterization setup for a 2-port LVR, from which the network parameters such as Z, Y and S parameters can be obtained. A typical plot of the associated transfer admittance Y21 is shown in Figure 1e, where it can be seen that the magnitude of Y21 is maximum at the resonant frequency f0.
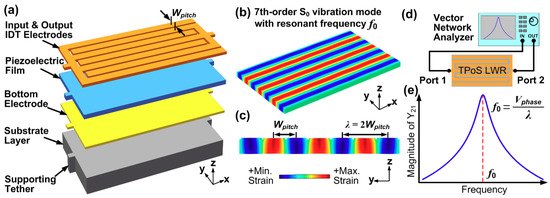
Figure 1.
a
b
c
0
f0
d
e
Y21 of a 2-port TPoS LVR.
The operation of resonant sensors hinges on the shift in resonant frequency due to a change in effective mass or stiffness of the resonant structure when subjected to a perturbation from the quantity of interest. There are three methods that are commonly used to detect the frequency shift of LVRs. The first utilizes the electrical characterization setup shown in Figure 1d, where the frequency response of the resonator is monitored by a network analyzer [10]. The second method involves detecting a change in amplitude of the output signal by exciting the resonator with an AC signal at a fixed frequency around the resonant frequency. This method essentially converts the shift in resonant frequency to a change in amplitude which is usually monitored using a lock-in amplifier [40]. The third method involves building an oscillator by connecting the resonator with the electronic amplifier to form a feedback loop. The output frequency of the oscillator can be readily monitored by a frequency counter [24]. Compared to the first two methods, the third method is more suitable for commercial applications as it does not require cumbersome characterization equipment [41]. It should be noted that, in resonant sensors characterized by all three methods mentioned above, higher Q is generally desired for better resolution [4]. Thus, it is of vital importance to maximize the Q of LVRs for sensing applications. In addition, boosting Q also lowers close-to-carrier phase noise in the application of oscillators [42], and improves roll-off characteristics in the application of RF filters [43].
2. Dominant Dissipations in LVRs
There are many dissipation mechanisms reported for LVRs, which are usually divided into two groups, namely intrinsic and extrinsic loss. Intrinsic losses are fundamental dissipative processes, thus dependent on the material properties, mode of resonance and internal structure. In contrast, extrinsic losses stem from interactions between the structure and the environment. Generally, the intrinsic losses, such as phonon-phonon or phonon-electron interactions, set the maximum Q achievable in bulk mode resonators [44]. Thermoelastic damping (TED) is one example of a type of intrinsic loss [45]. In most of the cases, the intrinsic losses are much smaller compared to extrinsic losses and easily get masked by the latter. Extrinsic losses mainly include anchor loss [46], ohmic loss, viscous loss [47] and surface loss [48], each of which will be detailed in the following part of this paper.
Quality factor (Q) is defined as the ratio of the maximum energy stored in the resonant system over the energy dissipated per cycle. The overall quality factor (Qtotal) of LVRs can be expressed by summing up the distinct dissipations [49]:
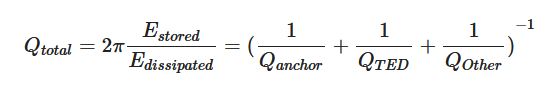
where Qanchor, QTED and Qother correspond to anchor loss, TED, and other losses, respectively. Unfortunately, there is scarcely any reported work on measuring individual loss (or individual Q) directly. Instead, only Qtotal, which describes the combined effect of different damping sources, can be obtained by measuring the amplitude-frequency or phase-frequency responses of the resonators. This brings about a huge challenge in analyzing the damping mechanisms present in LVRs because each constituent source of damping cannot be easily analyzed separately. However, if the dominant losses are much larger than other losses, then the other losses may be neglected in an approximation of Qtotal. In other words, the approximation considers only the dominant losses, which exhibit lower Qs and thus have more significant impact on Qtotal as indicated by Equation (2). It should be noted that Equation (2) emphasizes Qanchor and QTED because anchor loss and TED were found to play dominant roles in setting Qtotal in many LVRs [46][50][51][52][46,50,51,52]. Thus, this work mainly focuses on these two dissipation sources. However, other dissipations could become dominant in certain cases, which will be detailed in the following sections.
2.1. Anchor Loss
Generally, LVRs consist of free-standing resonant bodies that require mechanical support (dubbed as anchor). Thus, an anchor is defined as a mechanical structure that attaches the resonator body to the peripheral supporting frame. Anchor loss occurs when elastic energy propagates from the resonator body to the surrounding substrate through the anchors. If the total elastic energy stored in the resonator is given by Er and the energy propagating out via the anchors is given by El, then Qanchor can be computed using the following equation [53]:
For any LVR with a free-standing resonator body which is suspended by the supporting structures, anchor loss is unavoidable. This is true even if the anchor structure is placed at the positions where minimum displacement occurs (such points are normally referred to as nodal points). This is because the anchor structures have a finite size in practical cases rather than being an idealized infinitesimal point. It is widely reported that anchor loss plays the major role in setting the Q in most of LVRs [31][46][31,46].
2.2. Electrode-Related Loss and Thermoelastic Damping (TED)
For LVRs utilizing piezoelectric transduction, metal electrodes are necessary for actuation and detection of the Lamb wave in the resonator body. It was found there exists a damping mechanism related to the electrodes that has been associated with interfacial loss [54]. This electrode-related loss was confirmed by a demonstration in a 3.2-GHz overmoded LVR that the f·Q product can be pushed to 1.17 × 1013 by reducing the electrodes coverage to 0.57% [55]. To completely eliminate the electrode-related loss, some researchers proposed a capacitive-piezo transducer, which separates the electrodes from the resonator body by sub-micro gaps [56][57][56,57]. Applying this design strategy to a 940-MHz LVR leads to a 5× enhancement in Q, resulting an f·Q product 4.72 × 1012. These experimental results suggest that anchor loss alone cannot account for the measured Qs in LVRs, and the electrode-related loss also plays a significant role in setting Q. However, there is yet to be a solid universal explanation for the electrode-related loss observed in various types of LVRs. The complexity in analyzing electrode-related loss arises due to the uncertainty of the thermal properties and interfacial conditions for constituent metal and piezoelectric thin films [31][54][31,54]. One possible cause for the electrode-related loss is TED, which has been extensively studied for micro-resonators using electrostatic transduction [58][59][60][61][62][58,59,60,61,62]. For micro-resonators using piezoelectric transduction, it has been experimentally verified that TED plays a dominant role in setting Qs of a 1-GHz AlN LVR [51]. TED was also analyzed in a series of 140-MHz AlN-on-Si LVRs using finite-element analysis [50], where it was shown that TED made comparable contributions as anchor loss in setting the Qs of regular flat-edge LVRs. Thus, it is reasonable to consider TED as one of the significant source for electrode-related loss.
TED refers to an irreversible energy transfer process as elastic energy turns into heat [63][64][63,64]. The dissipation is caused by thermal gradients arising from the local volumetric change as the resonators vibrate. As such, this dissipation mechanism is absent for pure shear modes, where the volume of such modes does not change. This is the reason why reported f·Q products for Lamé bulk-mode silicon resonators can reach close to the limit set by intrinsic material loss [65]. In comparison, TED becomes more relevant for Lamb wave modes where longitudinal waves and shear waves are usually coupled in the resonator body. It is reported that QTED can be evaluated using the following equation [63]:
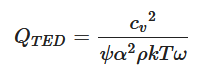
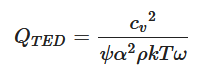
where cv denotes heat capacity per unit volume, ψ a constant related to the geometry of the resonator, α thermal expansion coefficient, ρ mass density, k thermal conductivity, T absolute temperature and ω angular frequency. Although Equation (4) holds for single-material devices, it can be extended to predict QTED of composite resonators (e.g., TPoS LVRs) by considering TED from each constituent layer with the help of finite-element analysis tools [50]. It was also found that TED from metals far exceeds that from semiconductors and dielectrics since metals generally exhibit larger thermal conductivities and thermal expansion coefficients [51][66][51,66]. Thus, it is reasonable to attribute TED to metal electrodes and simply ignore TED from piezoelectric and substrate layers as a reasonable approximation of Qtotal.
2.3. Other Dissipation Sources
Apart from anchor loss and TED, other dissipations such as ohmic loss and viscous loss could also become dominant for LVRs in certain cases.
Ohmic loss occurs when electrical currents pass through electrodes with low but non-zero resistance. As the operation frequency of LVRs increases, ohmic losses usually become more significant due to the smaller electrode width required for excitation of high-frequency Lamb waves. Larger electrical loss results in more heat generation causing non-linearity issues in LVRs which further limits the power handing capability [67]. To reduce ohmic loss, a common method is to increase the thickness the metal electrodes. However, a thick metal layer could negatively impact the indented vibration mode or cause additional damping [51]. An alternative solution is to use low-resistivity metals. It should be noted that trade-offs usually exist for choosing the metal materials for LVRs as many other design factors, such as acoustic impedance, power durability and complexity in terms of microfabrication process, also need to be taken into account.
Viscous loss occurs when a portion of kinetic energy transfers from the resonator to the surrounding molecules. It usually becomes larger as the surface to volume ratio of the resonator increases [47]. When operating LVRs in a fluidic medium, which is usually the case for biological sensing applications, viscous loss becomes the most dominant damping mechanism [21]. A common method to reduce viscous loss is operating the resonator in a shear mode as the shear acoustic wave does not displace the molecules perpendicular to the resonator surface [68].
References
- Langdon, R.M. Resonator sensors-a review. J. Phys. E Sci. Instrum. 1985, 18, 103–115. [Google Scholar] [CrossRef]
- Hauptmann, P. Resonant sensors and applications. Sens. Actuat. A Phys. 1991, 26, 371–377. [Google Scholar] [CrossRef]
- O’Sullivan, C.K.; Guilbault, G.G. Commercial quartz crystal microbalances—Theory and applications. Biosens. Bioelectron. 1999, 14, 663–670. [Google Scholar] [CrossRef]
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.Y.; Nabki, F. Micromachined Resonators: A Review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef] [PubMed]
- Nagaraju, M.; Gu, J.; Lingley, A.; Zhang, F.; Small, M.; Ruby, R.; Otis, B. A fully integrated wafer-scale sub-mm3 FBAR-based wireless mass sensor. In Proceedings of the 2014 IEEE International Frequency Control Symposium (FCS), Taipei, Taiwan, 19–22 May 2014; pp. 1–5. [Google Scholar]
- Zhang, M.; Huang, J.; Lu, Y.; Pang, W.; Zhang, H.; Duan, X. Solid-State Microfluidics with Integrated Thin-Film Acoustic Sensors. ACS Sens. 2018, 3, 1584–1591. [Google Scholar] [CrossRef]
- Liang, J.; Liu, Z.; Zhang, H.; Liu, B.; Zhang, M.; Zhang, H.; Pang, W. On-chip nanofluidic integration of acoustic sensors towards high Q in liquid. Appl. Phys. Lett. 2017, 111, 203501. [Google Scholar] [CrossRef]
- Yantchev, V.; Katardjiev, I. Thin film Lamb wave resonators in frequency control and sensing applications: A review. J. Micromech. Microeng. 2013, 23, 043001. [Google Scholar] [CrossRef]
- Qian, Z.; Vyas, R.; Hui, Y.; Rinaldi, M. High resolution calorimetric sensing based on Aluminum Nitride MEMS resonant thermal detectors. In Proceedings of the 2014 IEEE SENSORS, Valencia, Spain, 2–5 November 2014; pp. 986–989. [Google Scholar]
- Duan, Y.; Chang, Y.; Liang, J.; Zhang, H.; Duan, X.; Zhang, H.; Pang, W.; Zhang, M. Wireless gas sensing based on a passive piezoelectric resonant sensor array through near-field induction. Appl. Phys. Lett. 2016, 109, 263503. [Google Scholar] [CrossRef]
- Nan, T.; Hui, Y.; Rinaldi, M.; Sun, N.X. Self-Biased 215MHz Magnetoelectric NEMS Resonator for Ultra-Sensitive DC Magnetic Field Detection. Sci. Rep. 2013, 3, 1985. [Google Scholar] [CrossRef]
- Herrera-May, A.L.; Aguilera-Cortés, L.A.; García-Ramírez, P.J.; Manjarrez, E. Resonant magnetic field sensors based on MEMS technology. Sensors 2009, 9, 7785–7813. [Google Scholar] [CrossRef]
- Naik, A.K.; Hanay, M.S.; Hiebert, W.K.; Feng, X.L.; Roukes, M.L. Towards single-molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 2009, 4, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Bargatin, I.; Myers, E.B.; Aldridge, J.S.; Marcoux, C.; Brianceau, P.; Duraffourg, L.; Colinet, E.; Hentz, S.; Andreucci, P.; Roukes, M.L. Large-Scale Integration of Nanoelectromechanical Systems for Gas Sensing Applications. Nano Lett. 2012, 12, 1269–1274. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, M. Laterally Vibrating Piezoelectric MEMS Resonators. In Piezoelectric MEMS Resonators; Bhugra, H., Piazza, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 175–202. [Google Scholar] [CrossRef]
- Zuniga, C.; Rinaldi, M.; Khamis, S.M.; Johnson, A.T.; Piazza, G. Nanoenabled microelectromechanical sensor for volatile organic chemical detection. Appl. Phys. Lett. 2009, 94, 223122. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Q.; Chang, Y.; Pang, W.; Zhang, H.; Duan, X. Novel Gas Sensor Arrays Based on High-Q SAM-Modified Piezotransduced Single-Crystal Silicon Bulk Acoustic Resonators. Sensors 2017, 17, 1507. [Google Scholar] [CrossRef] [PubMed]
- Hui, Y.; Rinaldi, M. Fast and high resolution thermal detector based on an aluminum nitride piezoelectric microelectromechanical resonator with an integrated suspended heat absorbing element. Appl. Phys. Lett. 2013, 102, 093501. [Google Scholar] [CrossRef]
- Hui, Y.; Gomez-Diaz, J.S.; Qian, Z.; Alù, A.; Rinaldi, M. Plasmonic piezoelectric nanomechanical resonator for spectrally selective infrared sensing. Nat. Commun. 2016, 7, 11249. [Google Scholar] [CrossRef]
- Zuniga, C.; Rinaldi, M.; Piazza, G. Reduced viscous damping in high frequency Piezoelectric Resonant Nanochannels for sensing in fluids. In Proceedings of the 2011 IEEE 24th International Conference on Micro Electro Mechanical Systems, Cancun, Mexico, 23–27 January 2011; pp. 960–963. [Google Scholar]
- Ali, A.; Lee, J.E.Y. Electrical characterization of piezoelectric-on-silicon contour mode resonators fully immersed in liquid. Sens. Actuat. A Phys. 2016, 241, 216–223. [Google Scholar] [CrossRef]
- Daruwalla, A.; Wen, H.; Liu, C.; Jeong, H.; Ayazi, F. A piezo-capacitive BAW accelerometer with extended dynamic range using a gap-changing moving electrode. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 283–287. [Google Scholar]
- Daruwalla, A.; Wen, H.; Gong, M.; Ayazi, F. High-G and High-Bandwidth Bulk Acoustic Wave (BAW) Accelerometers Using a Metal-Less AlN-HARPSS Process With 95 nm Gaps. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Hui, Y.; Nan, T.; Sun, N.X.; Rinaldi, M. High Resolution Magnetometer Based on a High Frequency Magnetoelectric MEMS-CMOS Oscillator. J. Microelectromech. Syst. 2015, 24, 134–143. [Google Scholar] [CrossRef]
- Ghosh, S.; Lee, J.E. Eleventh Order Lamb Wave Mode Biconvex Piezoelectric Lorentz Force Magnetometer for Scaling Up Responsivity and Bandwidth. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 146–149. [Google Scholar]
- Nan, T.; Lin, H.; Gao, Y.; Matyushov, A.; Yu, G.; Chen, H.; Sun, N.; Wei, S.; Wang, Z.; Li, M.; et al. Acoustically actuated ultra-compact NEMS magnetoelectric antennas. Nat. Commun. 2017, 8, 296. [Google Scholar] [CrossRef]
- Ho, G.K.; Abdolvand, R.; Sivapurapu, A.; Humad, S.; Ayazi, F. Piezoelectric-on-Silicon Lateral Bulk Acoustic Wave Micromechanical Resonators. J. Microelectromech. Syst. 2008, 17, 512–520. [Google Scholar] [CrossRef]
- Pop, F.V.; Kochhar, A.S.; Vidal-Álvarez, G.; Piazza, G. Investigation of Electromechanical Coupling and Quality Factor of X-Cut Lithium Niobate Laterally Vibrating Resonators Operating Around 400 MHz. J. Microelectromech. Syst. 2018, 27, 407–413. [Google Scholar] [CrossRef]
- Song, Y.; Gong, S. Wideband RF Filters Using Medium-Scale Integration of Lithium Niobate Laterally Vibrating Resonators. IEEE Electron Device Lett. 2017, 38, 387–390. [Google Scholar] [CrossRef]
- Schaffer, Z.A.; Colombo, L.; Kochhar, A.S.; Piazza, G.; Mishin, S.; Oshmyansky, Y. Experimental investigation of damping factors in 20% scandium-doped aluminum nitride laterally vibrating resonators. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 787–790. [Google Scholar]
- Segovia-Fernandez, J.; Piazza, G. Damping in 1 GHz laterally-vibrating composite piezoelectric resonators. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 1000–1003. [Google Scholar]
- Piazza, G.; Stephanou, P.J.; Pisano, A.P. Piezoelectric Aluminum Nitride Vibrating Contour-Mode MEMS Resonators. J. Microelectromech. Syst. 2006, 15, 1406–1418. [Google Scholar] [CrossRef]
- Gokhale, V.J.; Roberts, J.; Raiszadeh, M. High performance bulk mode gallium nitride resonators and filters. In Proceedings of the International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Beijing, China, 5–9 June 2011; pp. 926–929. [Google Scholar]
- Pulskamp, J.S.; Rudy, R.Q.; Bedair, S.S.; Puder, J.M.; Breen, M.G.; Polcawich, R.G. Ferroelectric PZT MEMS HF/VHF resonators/filters. In Proceedings of the 2016 IEEE International Frequency Control Symposium (IFCS), New Orleans, LA, USA, 9–12 May 2016; pp. 1–4. [Google Scholar]
- Abdolvand, R.; Ayazi, F. Enhanced Power Handling and Quality Factor in Thin-Film Piezoelectric-on-Substrate Resonators. In Proceedings of the 2007 IEEE Ultrasonics Symposium Proceedings, New York, NY, USA, 28–31 October 2007; pp. 608–611. [Google Scholar]
- Fatemi, H.; Zeng, H.; Carlisle, J.A.; Abdolvand, R. High-Frequency Thin-Film AlN-on-Diamond Lateral–Extensional Resonators. J. Microelectromech. Syst. 2013, 22, 678–686. [Google Scholar] [CrossRef]
- Lin, C.; Chen, Y.; Felmetsge, V.V.; Senesky, D.G.; Pisano, A.P. Two-port filters and resonators on AlN/3C-SiC plates utilizing high-order Lamb wave modes. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 789–792. [Google Scholar]
- Tabrizian, R.; Ayazi, F. Laterally-excited silicon bulk acoustic resonators with sidewall AlN. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 1520–1523. [Google Scholar]
- Tu, C.; Lee, J.E.Y. A semi-analytical modeling approach for laterally-vibrating thin-film piezoelectric-on-silicon micromechanical resonators. J. Micromech. Microeng. 2015, 25, 115020. [Google Scholar] [CrossRef]
- Li, M.; Matyushov, A.; Dong, C.; Chen, H.; Lin, H.; Nan, T.; Qian, Z.; Rinaldi, M.; Lin, Y.; Sun, N.X. Ultra-sensitive NEMS magnetoelectric sensor for picotesla DC magnetic field detection. Appl. Phys. Lett. 2017, 110. [Google Scholar] [CrossRef]
- Van Beek, J.T.M.; Puers, R. A review of MEMS oscillators for frequency reference and timing applications. J. Micromech. Microeng. 2012, 22. [Google Scholar] [CrossRef]
- Qin, P.; Zhu, H.; Lee, J.E.; Xue, Q. Phase Noise Reduction in a VHF MEMS-CMOS Oscillator Using Phononic Crystals. IEEE J. Electron Devices Soc. 2016, 4, 149–154. [Google Scholar] [CrossRef]
- Kim, B.; Olsson, R.H.; Wojciechowski, K.E. AlN microresonator-based filters with multiple bandwidths at low intermediate frequencies. J. Microelectromech. Syst. 2013, 22, 949–961. [Google Scholar] [CrossRef]
- Chandorkar, S.A.; Agarwal, M.; Melamud, R.; Candler, R.N.; Goodson, K.E.; Kenny, T.W. Limits of quality factor in bulk-mode micromechanical resonators. In Proceedings of the 2008 IEEE 21st International Conference on Micro Electro Mechanical Systems (MEMS), Wuhan, China, 13–17 January 2008; pp. 74–77. [Google Scholar]
- Gokhale, V.J.; Gorman, J.J. Approaching the intrinsic quality factor limit for micromechanical bulk acoustic resonators using phononic crystal tethers. Appl. Phys. Lett. 2017, 111, 013501. [Google Scholar] [CrossRef] [PubMed]
- Segovia-Fernandez, J.; Cremonesi, M.; Cassella, C.; Frangi, A.; Piazza, G. Anchor Losses in AlN Contour Mode Resonators. J. Microelectromech. Syst. 2015, 24, 265–275. [Google Scholar] [CrossRef]
- Young-Ho, C.; Pisano, A.P.; Howe, R.T. Viscous damping model for laterally oscillating microstructures. J. Microelectromech. Syst. 1994, 3, 81–87. [Google Scholar] [CrossRef]
- Seoánez, C.; Guinea, F.; Castro Neto, A.H. Surface dissipation in nanoelectromechanical systems: Unified description with the standard tunneling model and effects of metallic electrodes. Phys. Rev. B 2008, 77, 125107. [Google Scholar] [CrossRef]
- Brand, O.; Dufour, I.; Heinrich, S. Resonant MEMS: Fundamentals, Implementation, and Application; Wiley: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Siddiqi, M.W.U.; Fedeli, P.; Tu, C.; Frangi, A.; Lee, J.E.Y. Numerical analysis of anchor loss and thermoelastic damping in piezoelectric AlN-on-Si Lamb wave resonators. J. Micromech. Microeng. 2019, 29. [Google Scholar] [CrossRef]
- Segovia-Fernandez, J.; Piazza, G. Thermoelastic Damping in the Electrodes Determines Q of AlN Contour Mode Resonators. J. Microelectromech. Syst. 2017, 26, 550–558. [Google Scholar] [CrossRef]
- Tu, C.; Lee, J.E.Y. Effects of cryogenic cooling on the quality factor of lamb wave mode aluminium nitride piezoelectric-on-silicon MEMS resonators. Sens. Actuat. A Phys. 2016, 244, 15–23. [Google Scholar] [CrossRef]
- Lee, J.E.Y.; Yan, J.; Seshia, A.A. Study of lateral mode SOI-MEMS resonators for reduced anchor loss. J. Micromech. Microeng. 2011, 21, 045010. [Google Scholar] [CrossRef]
- Hao, Z.; Liao, B. An analytical study on interfacial dissipation in piezoelectric rectangular block resonators with in-plane longitudinal-mode vibrations. Sens. Actuat. A Phys. 2010, 163, 401–409. [Google Scholar] [CrossRef]
- Gong, S.; Kuo, N.; Piazza, G. GHz AlN lateral overmoded bulk acoustic wave resonators with a f · Q of 1.17 × 1013. In Proceedings of the 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings, San Francisco, CA, USA, 2–5 May 2011; pp. 1–5. [Google Scholar]
- Yen, T.; Pisano, A.P.; Nguyen, C.T. High-Q capacitive-piezoelectric AlN Lamb wave resonators. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 114–117. [Google Scholar]
- Hung, L.; Nguyen, C.T. Capacitive-Piezoelectric Transducers for High-Q Micromechanical AlN Resonators. J. Microelectromech. Syst. 2015, 24, 458–473. [Google Scholar] [CrossRef]
- Candler, R.N.; Duwel, A.; Varghese, M.; Chandorkar, S.A.; Hopcroft, M.A.; Woo-Tae, P.; Bongsang, K.; Yama, G.; Partridge, A.; Lutz, M.; et al. Impact of geometry on thermoelastic dissipation in micromechanical resonant beams. J. Microelectromech. Syst. 2006, 15, 927–934. [Google Scholar] [CrossRef]
- Duwel, A.; Candler, R.N.; Kenny, T.W.; Varghese, M. Engineering MEMS resonators with low thermoelastic damping. J. Microelectromech. Syst. 2006, 15, 1437–1445. [Google Scholar] [CrossRef]
- Kim, B.; Hopcroft, M.A.; Candler, R.N.; Jha, C.M.; Agarwal, M.; Melamud, R.; Chandorkar, S.A.; Yama, G.; Kenny, T.W. Temperature Dependence of Quality Factor in MEMS Resonators. J. Microelectromech. Syst. 2008, 17, 755–766. [Google Scholar] [CrossRef]
- Ghaffari, S.; Ng, E.J.; Ahn, C.H.; Yang, Y.; Wang, S.; Hong, V.A.; Kenny, T.W. Accurate Modeling of Quality Factor Behavior of Complex Silicon MEMS Resonators. J. Microelectromech. Syst. 2015, 24, 276–288. [Google Scholar] [CrossRef]
- Darvishian, A.; Nagourney, T.; Cho, J.Y.; Shiari, B.; Najafi, K. Thermoelastic Dissipation in Micromachined Birdbath Shell Resonators. J. Microelectromech. Syst. 2017, 26, 758–772. [Google Scholar] [CrossRef]
- Chandorkar, S.A.; Candler, R.N.; Duwel, A.; Melamud, R.; Agarwal, M.; Goodson, K.E.; Kenny, T.W. Multimode thermoelastic dissipation. J. Appl. Phys. 2009, 105, 043505. [Google Scholar] [CrossRef]
- Zener, C. Internal Friction in Solids II. General Theory of Thermoelastic Internal Friction. Phys. Rev. 1938, 53, 90–99. [Google Scholar] [CrossRef]
- Tu, C.; Lee, J.E. Thermoelastic Dissipation in Etch-Hole Filled Lamé Bulk-Mode Silicon Microresonators. IEEE Electron Device Lett. 2012, 33, 450–452. [Google Scholar] [CrossRef]
- Lücke, K. Ultrasonic Attenuation Caused by Thermoelastic Heat Flow. J. Appl. Phys. 1956, 27, 1433–1438. [Google Scholar] [CrossRef]
- Lu, R.; Gong, S. Study of thermal nonlinearity in lithium niobate-based MEMS resonators. In Proceedings of the 2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 1993–1996. [Google Scholar]
- Pang, W.; Zhao, H.; Kim, E.S.; Zhang, H.; Yu, H.; Hu, X. Piezoelectric microelectromechanical resonant sensors for chemical and biological detection. Lab Chip 2012, 12, 29–44. [Google Scholar] [CrossRef]