AnisotCropy of the transmission media exerts a strong influence on the reflection and transmission coefficients. Anomalous refraction yields the consequence of polarization conversion for the refracted wave. We discuss this important physical pheneated by: Lin Fa and Meishan Zhaomenon by invoking practical interfaces between strongly anisotropic rocks, e.g., between O-shale and A-shale.
- VTI medium
- anisotropic media and interface
- anomalous refraction
- anomalous incident angle
- polarization conversion
- elliptical polarization
1.
Introduction
One of the basic properties of waves is polarization, which conveys valuable information in reflection, refraction, and other physical measurements. This certainly applies to both optical [1][2][3][4][5][1-5] and acoustic waves [6][7][8][9][6-9]. It has been established that reflection and refraction of acoustic waves between transversely isotropic media with a vertical axis of symmetry (VTI media) may yield anomalous refraction [10][11][12][13][10-13], which leads to profound implications in various applied fields [14][15][16][17][18][19][20][14-20], e.g., geophysics, seismic image and analysis, earthquake seismology, and underwater acoustics.
Anisotropy of the transmission media exerts a strong influence on the reflection and transmission coefficients. Anomalous refraction mostly occurs at the interface of the transversely isotropic media with strong anisotropy [21][22][23][24][25][26][27][21-27]. One such example is at the interface between anisotropic shale (A-shale) and oil shale (O-shale), as shown in Figure 1, where A-shale is considered as the incidence medium [25, [25][28]28]. Because the media are transversely isotropic, the wave properties in the y-direction are the same as those in the x-direction.
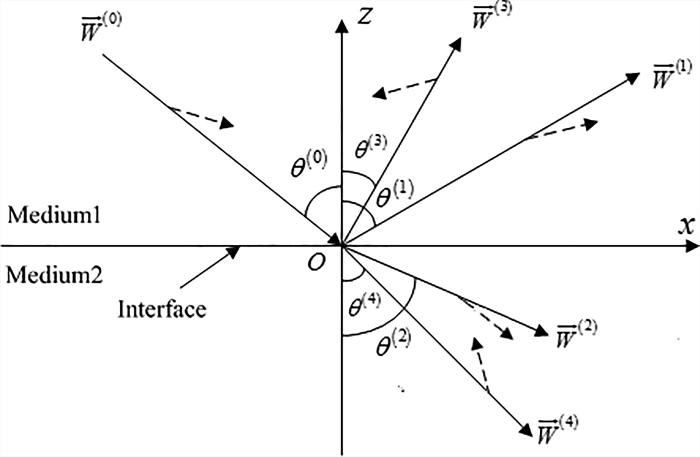
Figure 1. At the VTI-VTI interface, the incident P-wave causes reflection and refraction; this produces the reflected and refracted P-waves, as well as the reflected and refracted SV-waves. The dashed lines indicate the directions of polarization [Ref. [28]28].
Theoretical advancement in detecting abnormalities in refraction has been inspiring [22][33][22, 33]. One way of doing so is to examine the abnormalities in the angles of reflection and refraction. Based on Snell’s law, a fourth-order polynomial [22, 29] [22][29]has been established related to the angles of reflection and refraction of waves at the interface. For each given incident angle, the polynomial solutions (i.e., the sine of the refraction angles) may reveal any potential anomalies of the refraction and reflection.
Consider the interface of A-shale and O-shale. The sine of the angles of P-wave to P-wave refraction as a function of the incident angle is presented in Figure 2. It appears that, indeed, in the post-critical angle region, the polynomial solutions expose an anomalous incident angle at θ = 62.04o.
Now, the basic questions are how significant the anomalous refraction is in affecting the polarization state of the refracted wave and, from the influence of the anomalous refraction, what the converted polarization states are.
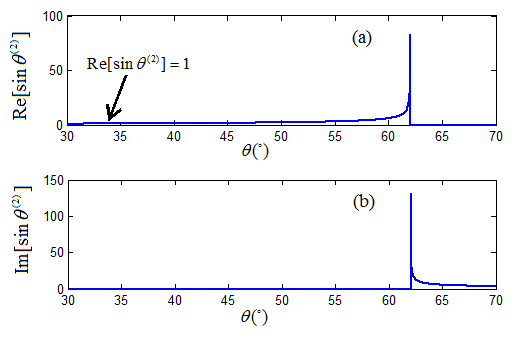
Figure 2. The sine function of the angle of reflection for P-wave to P-wave transmission versus incident angle at the interface of A-shale and O-shale, showing an anomalous incident angle at 62.04o [28][Ref. 28].
2. Poynting Vector
The Poynting vector has a direct connection to the polarization state of a wave signal on directional energy flow [28][30][28, 30]. Now, let’s consider the Poynting vector as an alternative in determining anomalous refraction and as a mean of connecting to polarization conversion.
For a P-wave propagating towards the interface and the induced waves at the interface, the Poynting vector is written as
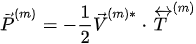 , (1)
, (1)
where m (= 0, 1, 2, 3, or 4) is the index for the various induced waves at the interface,  is the particle displacement velocity and
is the particle displacement velocity and 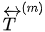 is the stress tensor of the incident P-wave and induced waves, which is determined by the physical properties of the media, including anisotropy.
is the stress tensor of the incident P-wave and induced waves, which is determined by the physical properties of the media, including anisotropy.
The z-components of the Poynting vector are the refracted and reflected components normal to the interface, which can be calculated from the reflection and refraction coefficients [20]. For a refracted P-wave, if its z-component is advancing its x-component by 90o, we call it a wave of right-rotational polarization (clockwise rotation). If its z-component is lagging its x-component by 90o, we call it a wave with a left-rotational polarization (anti-clockwise rotation).
The summarization of z-components of the Poynting vector for the induced waves can be calculated, which provides a cumulative effect for overall refraction and reflection,
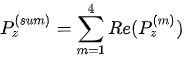 . (2)
. (2)
Consider A-shale as the incidence medium and O-shale as the transmission medium. At the interface between A-shale and O-shale, the z-component of the Poynting vector as a function of the incident angle is shown in Figure 3. The cumulative magnitude of the Poynting vector, the real part of its z-component, increases monotonically with respect to the incident angle until it reaches 62.04o, where it shows a clear abnormality. This is the same anomalous incident angle that was found and reported in the literature [21][22][31][32][21-22, 31-32].
It is worth pointing out that the refracted P-wave is a left-rotational polarized wave before reaching 62.04o that is the anomalous incident angle. At that point, it is converted to a right-rotational polarized wave. Obviously, this polarization conversion is a direct consequence of the anomalous refraction.
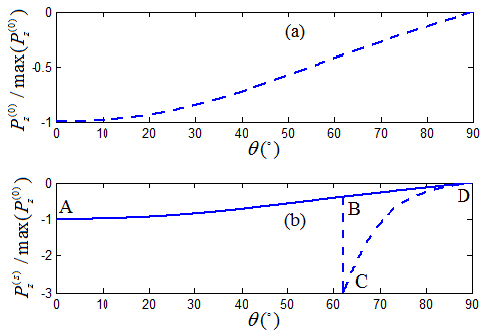
Figure 3. The z-component of the normalized Poynting vectors as a function of incident angle: (a) the incident P-wave, (b) the sum of all induced waves, where the dash-line shows an abnormality at 62.04o; the solid-line has an adjusted phase velocity solution of the refracted P-wave at 62.04o for continuity. Solid lines and dashed lines are overlapping prior to the anomalous incident angle at 62.04o [28][Ref. 28].
3. Elliptical Polarization Conversion
For the interface between A-shale and O-shale, there is a critical incident angle at 32.99o and an anomalous incident angle at 62.04o. It is this anomalous incident angle that leads to polarization conversion.
For VTI media such as A-shale and O-shale, propagations in the x-direction and y-direction are the same. The propagation properties are based solely on the x-direction and z-direction, as shown in Figure 1. The polarization coefficients (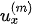 ,
, 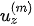 ) of the incident P-wave and the converted waves at the interface can be obtained from solving a two-dimensional Christoffel equation,
) of the incident P-wave and the converted waves at the interface can be obtained from solving a two-dimensional Christoffel equation,
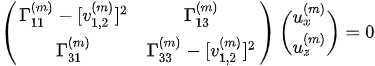 . (3)
. (3)
The matrix elements are functions of the incident angle and the parameters of the VTI media.
In the region prior to the anomalous incident angle, the transversely isotropic nature of the rock media yields two independent components of the inhomogeneous refracted P-wave:
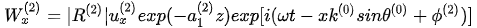 , (4)
, (4)
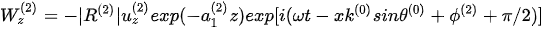 . (5)
. (5)
The refracted P-wave is now in a state of right-rotational polarization. The algebraic recombination of equations (4) and (5) yields a mathematical ellipse
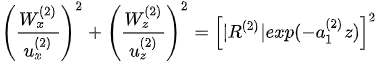 . . (6)
. . (6)
Following an elliptical trajectory, the rotation is counter-clockwise. Rotating the elliptical polarization trajectory around the z-axis produces a three-dimensional polarization elliptical sphere, as shown in the bottom part of Figure 4(a).
In the region after the anomalous incident angle, the transversely isotropic nature of the rock media yields two independent components of the inhomogeneous refracted P-wave:
 , (7)
, (7)
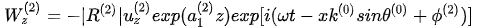 . (8)
. (8)
The refracted P-wave is now in a state of left-rotational polarization. The algebraic recombination of equations (7) and (8) yields a mathematical ellipse
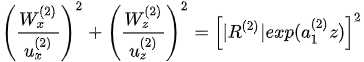 . . (9)
. . (9)
Following an elliptical trajectory, the rotation is counter-clockwise. Rotating the elliptical polarization trajectory around the z-axis produces a three-dimensional polarization elliptical sphere, as shown in the top part of Figure 4(a).
Obviously, passing through the anomalous incident angle at 62.04o, the refracted P-wave has experienced a polarization conversion from a clockwise elliptical polarization to an anti-clockwise elliptical polarization.
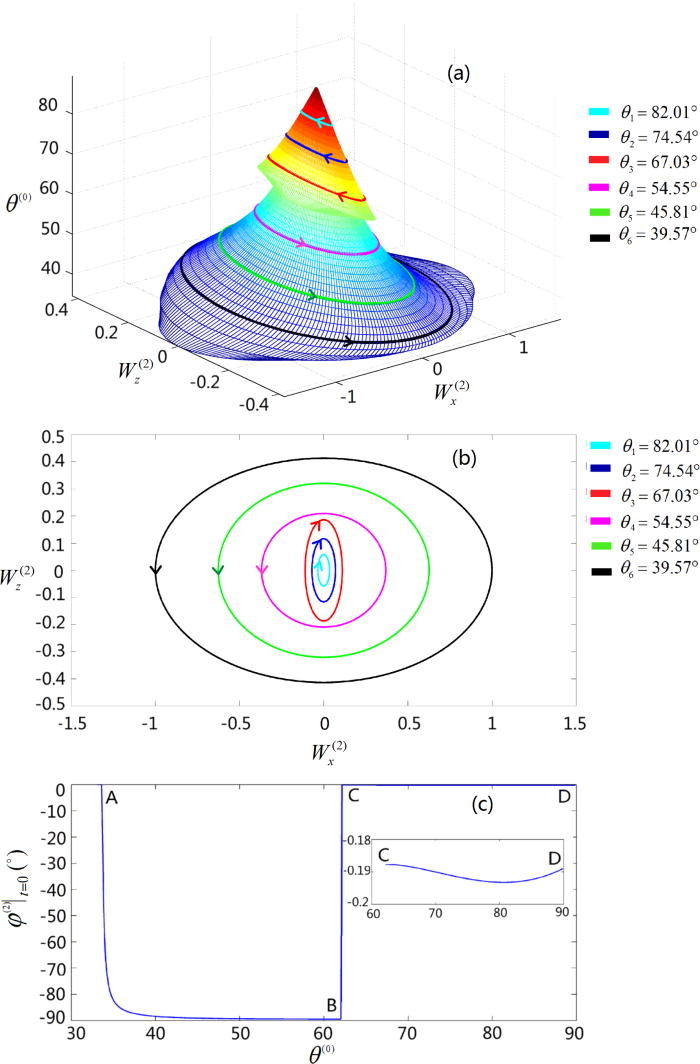
Figure 4. Polarization of an inhomogeneous refracted P-wave at the interface of A-shale and O-shale: (a) a three-dimensional polarization elliptical sphere, (b) the projection of the refracted wave onto the x-z plane, and (c) the initial state of the polarization rotational angle at the coordinate origin [31][Ref. 31].
4.
Weak Anisotropy
For VTI media under weak anisotropy, such as the interface between A-shale and T-sandstone (Taylor sandstone), the system does not exhibit any anomalous incident angle. Still, there is a critical incident angle at 48.34o. Following the same analysis as given in the last section, its polarization elliptical sphere is shown in Figure 5. In such a case, there is no observed phenomenon of polarization conversion.

Figure 5. Polarization of an inhomogeneous refracted P-wave at the interface of A-shale and T-sandstone: (a) a three-dimensional polarization elliptical sphere, (b) the projection of the refracted wave onto the x-z plane, and (c) the initial state of the polarization rotational angle at the coordinate origin [31][Ref. 31].
5.
Final Remarks
At the interface of certain transversely isotropic media, an anomalous incident angle may occur. It then leads to anomalous refraction and polarization conversion. Across an interface, this mostly happens for transversely isotropic media with strong anisotropy, leading to an anomalous incident angle, anomalous refraction, and polarization conversion. For example, there is anomalous refraction and polarization conversion at the interface between O-shale and A-shale, but no anomalous refraction at the interface between O-shale and T-sandstone, where the anisotropy is weak.
Observations of the various VTI media interfaces invite many open questions. The mechanism of anomalous refraction at the VTI interfaces is not fully understood at this moment.
First, it is not clear what degree of anisotropy is needed to induce the anomalous refraction and polarization conversion.
Second, there is a possibility of more than one critical angle at some interfaces. For example, at the interface between S-shale and C-sandstone (calcareous sandstone) [28], there are two critical incident angles found at 33.41o and 70.66o, but more than one anomalous refraction has not been found at the interfaces.
Finally, for some interfaces, there is anomalous refraction and polarization conversion for the refracted P-wave but not the refracted SV-wave. Explanations are needed for a comprehensive understanding of these interfaces.
References
- D. Singh, Fundamentals of Optics, 2nd ed., PHI Learning, 2015.
- N. K. Grady, J. E. Heyes, D. R. Chowdhury, Y. Zeng, M. T. Reiten, A. K. Azad, A. J. Taylor, D. A. R. Dalvit, H.-T. Chen, “Terahertz metamaterials for linear polarization conversion and anomalous refraction,” Science 340, 1304 (2013).
- R. M. A. Azzam and N. M. Bashara, Ellipsometry and Polarized Light, North-Holland, 1977.
- J. N. Damask, Polarization Optics in Telecommunications, Springer, 2004.
- D. Pye, Polarized Light in Science and Nature, Institute of Physics, 2001.
- A. Bacigalupo and M. Lepidi, “Acoustic wave polarization and energy flow in periodic beam lattice materials,” International Journal of Solids and Structures 147, 183-203 (2018).
- A. L. Shuvalov, “Topological features of the polarization fields of plane acoustic waves in anisotropic media,” Proc. R. Soc. Lond. A 454, 2911–2947 (1998).
- P. M. Shearer, Introduction to Seismology, Cambridge University Press, (2009).
- S. Stein and M. Wysession, An Introduction to Seismology, Earthquakes, and Earth Structure, John Wiley & Sons, 2009.
- L. Thomsen, “Weak anisotropy,” Geophys. 51, 1954-1966 (1986).
- J. Carcione, “Wave fields in real media: wave propagation in anisotropic, anelastic and porous media,” Elsevier, 2001.
- G. L. Backus, “Long-wave elastic anisotropy produced by horizontal layering,” J. Geophys. Res. 67, 4427 (1962).
- V. Ĉervenŷ, “Seismic Ray Theory,” Cambridge University Press, 2001.
- I. Tsvankin, “P-wave signatures and notation for transversely isotropic media: an overview,” Geophys. 61, 467 (1996).
- K. Y. Kim, K. H. Wrolstad, F. Aminzadeh, “Effects of transverse isotropy on P-wave AVO for gas sands,” Geophys. 58, 883 (1993).
- A. Rüger, “P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry,” Geophys. 62, 713 (1997).
- N. C. Banik, “Velocity anisotropy of shales and depth estimation in the North Sea Basin,” Geophys. 52, 1654 (1984).
- M. S. Sams, M. H. Worthington, M S. Khanshir, “A comparison of laboratory and field measurements of P-wave anisotropy,” Geophys. Prospect. 41, 189 (1993).
- L. Fa, L. Wang, L. Liu, Y. Zheng, Y. Zhao, N. Zhao, G. Li and M. Zhao, “Research progress in acoustical application to petroleum logging and seismic exploration,” The Open Acoustics Journal 6, 1 (2013), doi:1874-8376/13.
- L. Fa, M. Zhao, J. P. Castagna, Y. C. Liu, L. Wang, Y. Q. Wang and J. G. Sun, “On polarization of plane wave propagating inside elastic hexagonal system solids,” Science China: Physics, Mechanics & Astronomy 57, 1 (2014), doi: 10.1007/s11433-013-5363-3.
- Y. Zhao, N. Zhao, L. Fa and M. Zhao, “Seismic signal and data analysis of rock media with vertical anisotropy,” J. Modern Phys. 4, 11 (2013), doi:10.4236/jmp.2013.41003.
- L. Fa, R. Brown, J. Castagna, “Anomalous postcritical refraction behavior for certain transversely isotropic media,” J. Acoust. Soc. Am. 120, 3479 (2006).
- L. Fa and M. Zhao, “Recent progress in acoustical theory and applications,” in Understanding Plane Waves, Nova Science Publishers, Chapter 1, pp. 1-114, 2019.
- L. Fa and M. Zhao, “Recent development of an acoustic measurement system,” in Understanding Plane Waves, Nova Science Publishers, Chapter 2, pp. 115-147, 2019.
- L. Fa, J. P. Castagna, Z. Zeng, R. L. Brown and M. Zhao, “Effects of anisotropy on Time-Depth Relation in Transversely Isotropic Medium with a Vertical Axis of Symmetry,” Chin. Sci. Bulle. 55, 2241 (2010), doi: 10.1007/s11434-010-3186-4.
- L. Fa, Zhao, M., Liu, Y. C., Wang, L., Wang, Y. Q., and Sun, J. G., “Polarization of plane wave propagating inside elastic hexagonal system solids.” Sci. China-Phys. Mech. Astron. 57, 1 (2014).
- L. Fa, J. Tang, Q. Zhang, M. Zhang, Y. Zhang, M. Liang, and M. Zhao, “Reflection and refraction of acoustic wave at VTI-TTI media interface,” Frontiers of Physics 15, 22601 (2020), doi: 10.1007/s11467-019-0934-z.
- L. Fa, Y. Fa, Y. Zhang, P. Ding, J. Gong, G. Li, L. Li, S. Tang and M. Zhao, “Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave,” Scientific Reports 5, 12700 (2015), doi:10.1038/srep12700.
- L. Fa, J. Castagna, H. Dong, “An accurately fast algorithm of calculating reflection/transmission coefficients.” Sci. China-Phys. Mech. Astron. 51, 823 (2008).
- J. H. Poynting, "On the Transfer of Energy in the Electromagnetic Field,". Philosophical Transactions of the Royal Society of London 175, 343 (1884).
- L. Fa, J. Zhao, Y. Han and M. Zhao, “Polarization state of an inhomogeneously refracted compressional-wave induced at interface between two anisotropic-rocks,” J. of Acous. Soci. Ameri. 141, 1 (2017), doi:10.1121/1.4973410.
- L. Fa, J. Zhao, Y. Han, G. Li, P. Ding and M. Zhao, “The influence of rock anisotropy on the elliptical-polarization state of inhomogeneously refracted P-wave,” Science China Physics, Mechanics & Astronomy 59, 644301 (2016), doi:10.1007/S11433-015-00441-1.
- K. Helbig and M. Schoenberg, “Anomalous polarization of elastic waves in transversely isotropic media,” J. Acoust. Soc. Am. 81, 1235 (1987).
