Supercritical water gasification (SCWG) is a promising technology that has attracted the interest of many researchers around the world for the past two decades. The main application of SCWG is wet biomass, as no feed drying is required. Supercritical water (SCW) has singular properties, such as a very low dielectric constant, lower density than liquid water, and transport properties similar to those of a gas, especially the viscosity that increases the diffusion coefficient ^[1][2][3][1,2,3]. These properties make it favorable as a medium, reactant, solvent, and even as a catalyst to convert organic material into syngas, mainly composed of H₂, CO₂, CO, and CH₄.

Many studies on SCW gasification have been carried out, not only by experimentation but also by modeling and simulation. In fact, the general gasification reaction of an organic feed in SCW involves a series of coupled physical and chemical processes, including multiple reactions along with mass and heat transfer, in such a way that numerical simulation may overcome some drawbacks that occur in experimental methods to gain insight into the details of the gasification process under SCW conditions ^[4][5][6][4,5,6].

Similarly, there are review articles that deal with different aspects of SCWG, such as model compounds, lignocellulosic or microalgae biomass, types of reactors, energy and exergy, thermodynamics, catalysts, techno-economics, hydrogen production, modeling, and simulation ^{[6][7][8][9][10][11][12][13][14][15][16][17]}[6,7,8,9,10,11,12,13,14,15,16,17], but there are few references to heat transfer in SCWG processes, especially at the lab scale, which is used most frequently in experimental studies carried out so far. In this regard, the heating rate/time applied to a specific reactor and how heat is transmitted from the energy source to the stream containing organic material and water that suffers a transition from subcritical to supercritical are crucial to understand the phenomena occurring inside the reactor and for scaling up.

Therefore, the reactor type applied to supercritical water gasification (SCWG) is of utmost importance. Three main types of reactors have been used. First, batch reactors with or without a stirrer, then tubular reactors, and finally fluidized-bed reactors. Regarding the topic of this review, the latter type of reactor allows the best heat transfer and appears to avoid or reduce some detected problems, especially in tubular reactors, such as plugging due to char formation [18]. In fact, char formation has been reported to occur at 200 °C and tar is formed mainly from 300 °C to the critical temperature of water [3], while other researchers have found that char and tar form more quickly between 350 and 370 °C [19]. These shortcomings are related to the heating section of the reactor, which is generally performed by an electric furnace. However, heat transfer in a fluidized bed is more complex than in a tubular reactor as it implies fluid, particles, and a reactor wall that includes mechanisms affecting all pairs of these elements (fluid-particles, etc.) due to heterogeneous flow within the bed [20]. Furthermore, in the operation of fluidized bed under SCW conditions, there is instability of the gas product, nonuniform temperature distribution, and particle overflow [21]. In addition, when SCWG is simulated in fluidized-bed reactors, the existing correlations of heat transfer may not be appropriate because the applicability and operation conditions can have a large deviation from those found in conventional fluidized beds, which requires more experimental research. There are a number of additional studies on this type of reactor ^{[6][9][10][11][12]}[6,9,10,11,12], although the design of SCWG fluidized-bed reactors is currently incomplete, especially with respect to the heat transfer characteristics of SCW [22]. Further study on fluidized-bed reactors is required, as it is a promising type of reactor to be used on SCWG, especially when the technology is more developed and investment may be justified, which is easier using a simpler based-on tube reactor as next described, and fluidized-bed reactors are beyond the scope of this paper.

One of the aspects regarding tubular reactors is how to heat the stream entering the reactor and the inside of the reactor to avoid the operation problems mentioned above. The residence time in the tubular reactor is about a few seconds, which is much shorter than the reaction time in a batch reactor, where it is between minutes and hours. In fact, a prolonged reaction time leads gasification reactions to chemical equilibrium, thus greatly increasing the gas yield [23], one of the main objectives in SCWG. In spite of such a favorable potential result, it does not seem to be a good reactor type for scaling up the reactor to move the technology to an industrial scale. In addition, heat recovery in a batch reactor becomes difficult, but not in a continuous-flow reactor, so the latter concept is more appropriate for commercial application. Despite this, several studies using batch reactors can be found in the literature ^{[24][25][26][27][28][29]}[24,25,26,27,28,29].

Therefore, most of the experimental research on SCWG has been carried out using tubular reactors ^{[30][31][32][33][34][35][36][37][38]}[30,31,32,33,34,35,36,37,38] with the aim of addressing a future scale of the process. However, the design of this type of reactor may and must be improved to apply it to SCWG technology. One of the aspects related to heat transfer in the SCWG fluidized-bed reactor is the high heating rate, which is probably the solution to avoid the main operation problems in tubular rectors. Therefore, heat transfer and, specifically, the heating rate of the feed must be analyzed to improve the behavior of this type of reactor.

2. Heat Transfer Deterioration in SCWG Experiments

The abrupt changes that water undergoes in its physical properties near the critical point contribute to the deterioration of heat transfer, due to the decrease in turbulent thermal conductivity and eddy viscosity, leading to lower turbulent heat flux and therefore higher surface temperatures [39]. This deterioration may be the result of a significant density variation near the critical point that deforms the velocity profile, flagging the turbulence [5], or even due to the thickening of the viscous underlayer depending on the fluid flow rate [40]. Many research works, mainly performed numerically, have been published on this phenomenon, known as heat transfer deterioration (HTD) ^{[41][42][43][44][45][46][47]}[41,42,43,44,45,46,47]. Recently, Wang et al. [48] obtained, by simulation, that semicircular heating decreased the degree of HTD due to the greater turbulence produced by the greater density difference between the heating side and the adiabatic side. Figure 1 illustrates the trend of the physical properties of water versus temperature at 23 MPa and 25 MPa, obtained by [21], where the maximum values of specific heat and thermal conductivity define different pseudocritical temperatures; in fact, each pair (P, T) above the critical point leads to a pseudocritical point. The pseudocritical temperature increases as the (supercritical) pressure increases, and at this point and on, there is no longer a difference between the liquid and gas/vapor phases. Regarding the change in water properties, at 25 MPa, a temperature variation from 377 °C to 393 °C, that is, about 4.2%, leads to a density change from 488.85 kg/m³ to 194.89 kg/m³, i.e., roughly 60% [49]. Therefore, viscosity and density are greatly reduced from subcritical to supercritical water conditions, thus improving mass transfer [50], although thermal conductivity decreases and specific heat capacity changes a lot [2]. The low flow rate in lab-scale reactors leads to deterioration in heat transfer due to buoyancy forces and flow acceleration, which is promoted by the change in physical properties during heating; therefore, this aspect should be taken into account when improving heat transfer performance. In lab-scale research, low mass flow rates are commonly used, and although a tubing with a small internal diameter (ID) is also utilized, the fluid velocity is quite low, so turbulence is almost nonexistent. A lower heating rate leads to longer residence and reaction times, but there is still a large section in the reactor with a lower temperature, thus forming char and tar. Therefore, it seems that there must be a trade-off between reaction time and heating rate with respect to the temperature increase experienced by the stream fed to the reactor, since the reactants are heated up at a certain rate clearly lower than the heating rate programmed for the heating process unit. As a consequence, a lapse of time is required to reach the reaction temperature. Consequently, this time needs to be minimized in the experimental facilities, thus inhibiting the formation of char and tar. Heating of the reactor is mostly performed by external heating, typically with an electric radiant furnace, although it could also be carried out by internal heating from the fuel value of the feedstock in an autothermal operation, using a fraction of the gas produced in the process or even with an external fuel. These other options are not common at lab scale, and electric heating is most frequently used at lab scale, normally housing the reactor inside an electric furnace. In addition, preheating the reactor inlets and ducts upstream of the reactor is usually conducted using resistive wires or auxiliary radiant heaters [9]. Electric radiant furnaces are designed by considering a number of sections, each one with a temperature PID controller based on a thermocouple measuring the external wall of the reactor and using a thyristor or state-solid relay (SSR) as a final control element to switch on/off the resistor inside the correspondent furnace section. Several sections involve more sets of thermocouples, controllers, and SSR, but better temperature control can be achieved inside the furnace. It is common to preheat the electric furnace before entering the feed stream containing the organic compounds to approach the final reaction temperature. In addition, the heating may not be uniform throughout the reactor, as it has several meters of length, where liquid feed converts into supercritical in a section of reactor, so the properties change inside the reactor and oblige to activate the different SSR more or less, as these are linked to the controllers and thermocouples of each heating section. In this sense, a nonuniform temperature distribution along the pipe is another consequence of the slow and initially dense feed that may occur in the inlet zone of the reactor housed in the electric furnace. This non-uniformly heated tubular reactor needs to be treated as a transition process when modelling, despite steady-state equations frequently found in the literature to describe this process. As mentioned above, the measurement of temperature of the stream at the reactor outlet is typically performed on the tubing external surface, and not inside the stream at high temperature and pressure, mainly for safety reasons, so the real fluid temperature is not usually measured in the section with the highest pressure and temperature. Beyond the inlet zone of the reactor, another additional aspect that occurs is related to the transition from the subcritical to the supercritical fluid state, i.e., the effect of change in physical properties that leads to an intermediate zone inside the reactor, which is not well defined and is difficult to experimentally determine. A low Reynolds number characterizes the fluid flow, leading to a laminar flow regime where heat transfer is not effective enough and convection controls the heat transmission process. Additionally, as the temperature increases progressively and the transition from subcritical to supercritical states takes place, the Reynolds number changes significantly along the reactor as a result of the notable change experienced in both the density and the dynamic viscosity of water. However, the flow regime remains laminar. In fact, when the Reynolds number is expressed as a function of the mass flow rate, which is constant, the only property that affects the Reynolds number is the dynamic viscosity, and this changes from 10⁻³ Pa·s to about 3 × 10⁻⁵ Pa·s (Figure 1). Thus, the Reynolds number would be multiplied by a factor of up to 30 through the reactor, and still laminar flow regime is below 2300 (i.e., laminar flow), or perhaps slightly over, but always too low to achieve effective turbulent mixing. Furthermore, several researchers have reported deterioration in heat transfer [51] for SCW when the flow regime is laminar at a temperature higher than the pseudocritical temperature, where the properties of SCW are more gas-like at a given operating pressure. In this regard, at such low velocity, the effect of mixing is negligible, and heat transfer is poor. As Kawasaki et al. [52] pointed out, the low mixing rate due to a low Reynolds number results in slow heating of the fluid through the stage in which the subcritical condition takes place, involving a low reaction rate and the appearance of primary and secondary nucleation that forms large char particles during the heating period. The problem becomes more complex if the tubular reactor is vertically positioned instead horizontally, since the great change in density implies a significant buoyancy effect at low flow rates and flow acceleration at high flow rates; at laboratory scale, the first effect is the most relevant. Under these conditions, the velocity increases near the wall region so that the velocity profile is flattened, reducing the turbulent heat transfer coefficient, thus causing further deterioration of the heat transfer [53]. Moreover, some local turbulence may occur due to the higher flow near the wall produced by natural convection induced by gravity force related to the weighty change in density close to the pseudocritical temperature despite the laminar flow regime due to the low Reynolds numbers [51]. (more sections are available in the original paper published in Energies)

3. Next Perspectives in Design

On the basis of the concept of a tubular reactor that may be extended to a multitube reactor, some ideas may be proposed and discussed to enhance heat transfer by designing involved process units. There must be fast and effective heating inside the reactor, where fluid flows, and that is the zone where the highest resistance to heat transfer is found. In this way, a new reactor design could enhance this aspect. Here, process intensification may play an important role and there are a number of possibilities. First, a nonmetallic reactor made of quartz could be used, for instance, instead of metallic alloys, such as Inconel 600 or 625, AISI 316, or different Hastelloy, along with microwave heating, where the frequency would be adjusted to selectively supply the energy required by the reactants to allow their molecules to overcome the activation energy, which is the energy barrier. This could be more efficient for the energy supply required for the reactions and even for the heating of all of the streams, which would take place more quickly and selectively. In fact, considering an Arrhenius-type kinetic law, heating must serve to increase the temperature term found in the exponential function. This heating way, against electric heating by resistances (directly disposed on the tube wall or applied externally to the reactor and transmitted by radiation), avoids temperature gradients that produce an energy distribution, and hence energy losses. Second, a maximum specific surface area should be used to further improve mass and heat transfer. Thus, different and specific heat transfer equipment and reactors may be applied to achieve this target. The diffusion-bonded compact heat exchanger is a compact type heat changer that can operate up to 100 MPa or 900 °C, reducing up to 90% of the area compared to multitube heat exchangers, where the heat transfer area per unit volume is at least 1000 m²/m³, so the size can be reduced to 85% compared to conventional multitube heat transfer ^[54][77]. This heat exchanger could be used as both a microreactor and a microheat exchanger. Mortean et al. ^[55][78] evaluated heat transfer in a diffusion-bonded compact heat exchanger at low flow rates for low Reynolds numbers, mainly in the laminar flow regime, and more recently Sarmiento et al. ^[56][79] extended the study in a series of Reynolds numbers between 2600 and 7500, thus covering the transition to a turbulent flow regime. 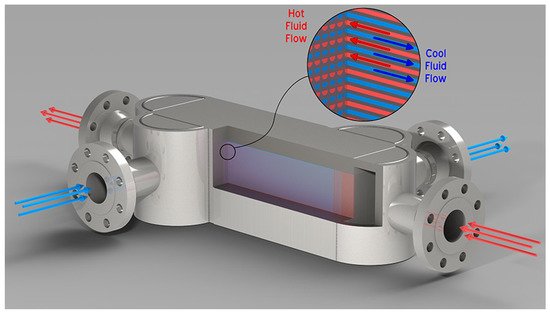Currently, there are already several manufacturers ^[57][58][80,81], and Figure 27 shows the details of one of them. Likewise, microchannel reactors show a surface-to-volume ratio much larger than that of multitube reactors, which could be the logical selection for scaling up as tubes may be multiplied as the flow rate does, especially considering that the lower thickness of small ID tubes has mechanical resistance similar to that of tubes with larger ID and thickness under the severe conditions of SWG. The use of microreactors with thousands of microchannels allows for good mixing of reactants and the removal of heat is more efficient. There is another possibility of a micro reactor plus a micro heat exchanger. Regarding heat transfer in lab-scale tests, apart from using a different energy source, the use of compact devices, such as those mentioned above, could allow for better heat transfer performance using flue gas coming from a burner at high temperature acting as the hot fluid. In addition, the design of a series of heat exchangers should be performed, especially the one where the transition from subcritical to supercritical state takes place because of the strong change in the physical properties of the feed, mainly wet biomass with a high proportion of water. Furthermore, the use of static mixers promotes turbulence without mobile parts and presents resistance to interphase mass transfer that is noticeably smaller than in conventional equipment, such as stirred tanks, and the flow pattern is close to the plug flow and is more uniform, and the residence time of the molecules is closely distributed. As a consequence, the collisions of molecules will be more effective and energy losses will be lessened ^[59][82]. It is clear that despite the proposed devices being real, further research must be carried out to improve their performance and applicability and, in particular, to reduce capital costs so that they may be used at full scale. (see references in the original paper published in Energies)