Power Estimation for Electric Vehicles’s Lithium-Ion Batteries: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Amina Yu and Version 5 by Ruohan Guo.

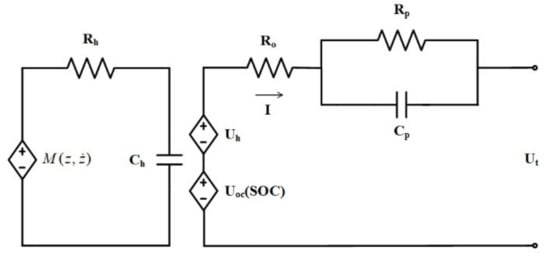
State of power (SOP), as one of the key states of lithium-ion batteries, is defined as the peak power capability that a battery could deliver or receive over a prediction window while keeping the battery within the safe operating area [9]. By this definition, most existing methods for online SOP estimation employ an equivalent-circuit model (ECM) to simulate battery dynamic behaviour in a prediction window and assume batteries operating at three operation modes, namely the constant current (CC), constant voltage (CV), and constant current constant voltage (CCCV) modes. Accordingly, three online SOP estimation methods have been developed with different basic principles, and many efforts have been made in the past decades for the improved performance of online SOP estimation from three aspects: (1) model structure; (2) online parameter identification technique; and (3) SOP estimation algorithm. 

  • online state of power estimation
  • equivalent-circuit model
  • lithium-ion battery
  • electrical vehicle
  • review

1. Basic Principle of Online SOP Estimation

1.1. SOP Estimation at a Constant Current Mode

In online SOP estimation at a CC mode, a battery is supposed to continuously operate at a constant current throughout a prediction window [1]. Assume the prediction window (ranging from time k to k + L), battery current, and terminal voltage during this period can be depicted in Figure 1, where discharge current is assumed to be positive, while charge current is negative. It can be seen that the terminal voltage of a battery will monotonically decline (or grow) in the CC discharge (or charge) mode. Therefore, SOP depends on the power capability at the end-of-window. Compared with other constraints (e.g., current limit and SOC limit), voltage limit is a major concern in the CC mode based online SOP estimation, which requires accurately predicting battery terminal voltage at the end of a prediction window, based on the employed ECM. Battery SOP is determined once battery terminal voltage reaches its lower (or upper) cut-off value, namely Ut,min (or Ut,max) [2].
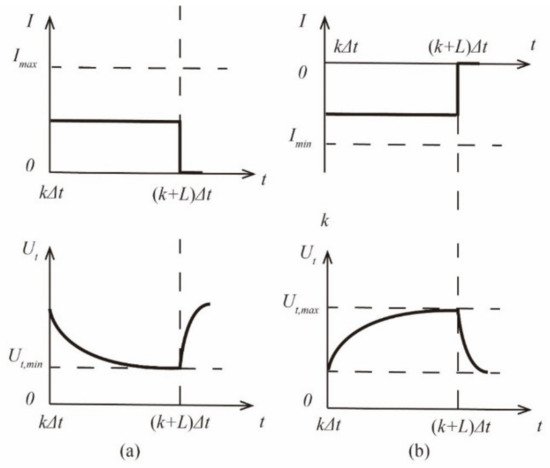
Vehicles 04 00001 g001 550
Figure 1. Battery current and terminal voltage in SOP estimation at a constant current mode: (a) discharge; (b) charge.

1.2. SOP Estimation at a Constant Voltage Mode

In online SOP estimation at a CV mode, a battery is forced to continuously operate at its lower (or upper) cut-off voltage throughout a prediction window [3]. As depicted in Figure 2, the peak discharge current would monotonically decrease, while the peak charge current exhibits an opposite trend in this period. Therefore, accurately capturing the current variation trend is required, based on the employed ECM during the prediction window, while the battery terminal voltage is deemed to be kept at Ut,min (or Ut,max).

Vehicles 04 00001 g002 550
Figure 2. Battery current and terminal voltage in SOP estimation at a constant voltage mode: (a) discharge; (b) charge.

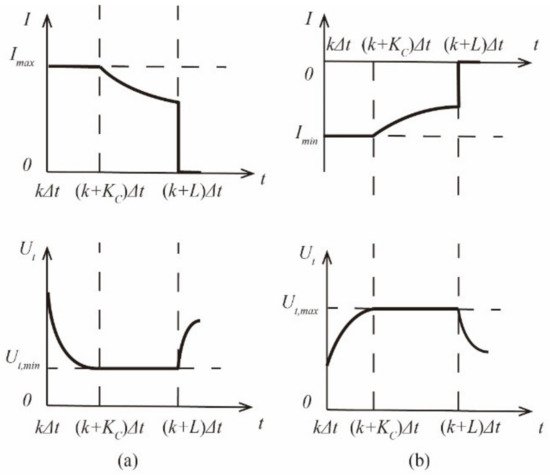
1.3. SOP Estimation at a Constant Current Constant Voltage Mode

In online SOP estimation at a CCCV mode, a battery is operating at current limit at a CC mode at the very beginning and will shift from the CC mode to a CV mode once battery terminal voltage reaches voltage limit, as depicted in Figure 3. It can be observed that pinpointing the timing the shift from CC to CV mode is the key to work out the peak power of the CCCV mode. Such critical timing occurs when a battery is operating at its pre-set current limit, while its terminal voltage reaches Ut,min (or Ut,max). Afterwards, the battery will turn to CV mode, and the load current has to reduce to avoid breaking the pre-set voltage limit [4].

Vehicles 04 00001 g003 550
Figure 3. Battery current and terminal voltage in SOP estimation at a constant current constant voltage mode: (a) discharge; (b) charge.

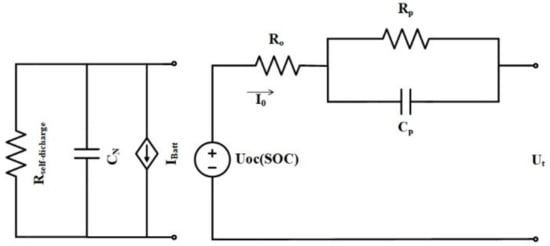
2. Improvements on Equivalent Circuit Model

(ECM) -Based Method for Online SOP Estimation

2.1. Improvements on Battery Modelling

2.1.1. Improved 1-RC Model

Vehicles 04 00001 g004 550
Figure 4. 1-RC model.
In pursuit of a more accurate battery model in SOP estimation, some specially designed components are introduced into a basic 1-RC model to reflect battery diffusion phenomenon, hysteresis effect, and self-discharge process.
In [5], a 1-RC model with diffusion resistance, as shown in Figure 5, is constructed to mimic battery diffusion phenomenon in a low frequency region for long-term SOP estimation. The time-dependent diffusion resistance is characterised based on a mass of experimental data. As an advantage, the alteration of the model structure will not influence the derivation of peak discharge and charge current. The experimental results show that the proposed model could effectively improve the SOP estimation accuracy in a prediction window over 10 s. However, the adaptability and robustness of the empirically-derived diffusion resistance need to be further examined under different driving scenarios.
Vehicles 04 00001 g005 550
Figure 5. 1-RC model with diffusion resistance [5].
In [6][7][8][9], a 1-RC model with one-state hysteresis, as shown in Figure 6, is employed to capture battery hysteresis effect between battery charge and discharge trajectories. The peak power characteristics of LiFePO4 batteries are investigated under different operating conditions in [6]. According to the authors, the absence of hysteresis dynamics in basic 1-RC models will significantly affect SOP estimation of LiFePO4 batteries. Referring to [10], from the same authors, 1-RC model with one-state hysteresis is found as the best choice for LiFePO4 batteries, amid 12 commonly used ECMs, which offsets a notable voltage hysteresis and alleviates the model error by 7.9%, compared to basic 1-RC model. However, a main challenge of this model for online SOP estimation lies in that it is unable to directly formulate an analytical expression of peak discharge and charge current, due to the high nonlinearity of the current-dependent hysteresis voltage. Consequently, a numerical method, such as the bisection and Levenberg–Marquardt algorithms, is often resorted to, in order to solve the peak currents from a strong nonlinear equation.
Vehicles 04 00001 g006 550
Figure 6. 1-RC model with one-state hysteresis [6][7][8][9].
In [11], a joint estimation algorithm of both SOC and SOP is proposed, based on a 1-RC model considering the self-discharge phenomenon. As shown in Figure 7, a runtime-based model (in the left part) comprises of a capacity, self-discharge resistance, and controlled current source in parallel, aiming to simulate the effects of battery cycling and calendar aging on available battery capacity in the long run.
Vehicles 04 00001 g007 550
Figure 7. 1-RC model considering self-discharge phenomenon [11].
In [12], the authors state that the model error of a basic 1-RC model can result from a broad-frequency band. In view of this, a 1-RC model with a moving average noise, as shown in Figure 8, is proposed.
Vehicles 04 00001 g008 550
Figure 8. 1-RC model with a moving average noise [12].
Since Gaussian white noise covers a whole frequency range, the proposed model takes advantages of this nature to emulate the model error through a linear combination of a sequential Gaussian white noise in a moving average window. After being transformed to a linear regression form, the weight vector of the moving average model can be online regressed, together with other model parameters, to realise adaptability, which contributes to the precision of SOP estimation. Compared with basic 1-RC model, the 1-RC model with a moving average noise could strikingly reduce the voltage error under various load profiles.
Other than the aforementioned improvements on model structure, different dependencies of 1-RC model parameters can be calibrated over a whole battery operating range to enhance model accuracy and robustness.
In [13][14], a 1-RC model incorporating the Butler–Volmer equation (BVE), as shown in Figure 9, is proposed to take into account the current dependency on charge transfer resistance, due to the outstanding discharge capability of lithium-ion batteries. The BVE describes the nonlinear relationship between overpotential and current in a charge transfer process; thus, the growing trend of battery polarisation voltage can be better reproduced via the proposed model at a large load current. However, the application of the BVE remarkably raises the computational complexity of SOP estimation, which generally requires a numerical method to solve the peak current estimation and, thus, demands strong computational power from BMSs.
Vehicles 04 00001 g009 550
Figure 9. 1-RC model incorporating Butler–Volmer equation [13][14].
In [15], a so-called migrated 1-RC model, as shown in Figure 10, is proposed to improve the robustness of SOP estimation against uncertainties from battery aging and temperature variation, where the model parameters are all characterized as three-dimensional surfaces of SOC and temperature.
Vehicles 04 00001 g010 550
Figure 10. Migrated 1-RC model [15].
Two particle filtering-based linear migrations are devised to adjust model parameters over battery lifetime. However, they totally require 10 migration coefficients to be tuned in parameters recalibration, thereby producing a heavy computational burden for BMSs in EV applications.
In [16], an improved 1-RC model with multi-dependent OCV, as shown in Figure 11, is established for SOP estimation, in order to compensate the distortion phenomenon of OCV–SOC curve. The multi-dependent OCV, is modelled as a multi-dimensional map of SOC, temperature, aging factor, and hysteresis factor to adapt complex load conditions, which is advantageous to both online SOC and SOP estimation.
Vehicles 04 00001 g011 550
Figure 11. 1-RC model with multi-dependent OCV [16].
For the readers’ convenience, the benefits and drawbacks of the improved 1-RC models have been listed in Table 1.
Table 1. Benefits and drawbacks of the improved 1-RC models in online SOP estimation.
  Improved 1-RC Models Benefits Drawbacks
Structure

improvements		 1-RC model with diffusion resistance [5]
  • Enhance the model accuracy in describing diffusion process
  • Remain low model complexity
  • Require a mass of tests to model diffusion resistance
  • Lack of robustness
1-RC model with one-state hysteresis [6][7][8][9]
  • Offset hysteresis voltage
  • Increase model complexity
  • Increase computational cost in SOP estimation
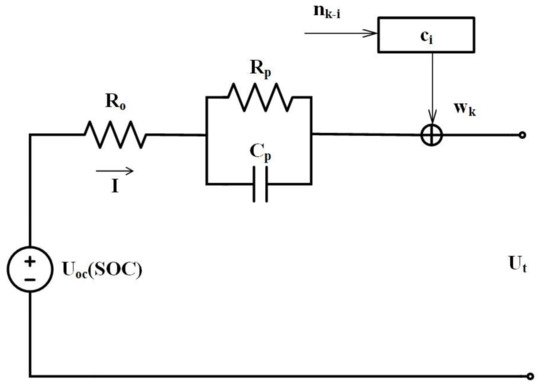
1-RC model considering self-discharge phenomenon [11]
  • Enhance the model robustness against battery calendar aging and cycling aging
  • Require a mass of data to establish battery aging model
  • Lack of robustness under different driving experience
1-RC model with a moving average noise [12]
  • Enhance the model accuracy under dynamic load profiles
  • Barely increase the computational cost in SOP estimation
  • Increase model parameters
  • Model accuracy depends on the length of the moving horizon
Consider

parameter

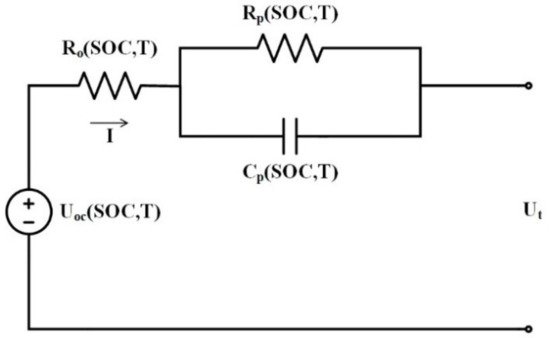
dependencies		 1-RC model incorporating Bulter-Volmer equation [13][14]
  • Enhance the model accuracy against current effect
  • Largely increase model complexity
  • Increase computational cost in SOP estimation
Migrated 1-RC model [15]
  • Enhance the model accuracy against the effects of SOC and temperature
  • Require a mass of tests to extract parameter dependencies
  • Largely increase model parameters
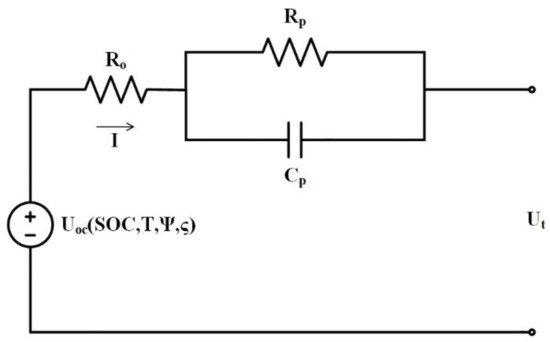
1-RC model with multi-dependent OCV [16]
  • Enhance the model robustness of OCV-SOC curve against the effects of temperature, hysteresis and battery aging
  • Require a mass of tests to extract parameter dependencies
  • Increase model parameters

2.2. Improved Online Parameter Identification Technique

Model parameters of a battery feature slow-varying characteristics and are jointly influenced by a series of factors (e.g., SOC, current, and temperature). Considering the accuracy, adaptability, and computational efficiency for EV applications, online parameter identification techniques offer more superiority over offline techniques, which could only be implemented in a laboratory environment and may gradually lose fidelity during service. By far, online parameter identification techniques can be divided into two main groups: recursive and non-recursive methods [17].
Because of strong adaptability and low computational effort, recursive methods, such as the recursive least-square (RLS) algorithm and Kalman filter (KF) family, are favoured as the preferred candidate for model parameterisation in SOP estimation. On the other hand, this type of methods requires model mathematical expression to be converted into a linear regression form, with respect to model parameters and measurable signals, which may not be suitable for some ECMs with high nonlinearity. In [18], the authors proposed a RLS algorithm with an adaptive ratio vector for online model parameterization in pack-level SOP estimation. The RLS algorithm is employed to provide mean parameters estimation at a pack level, while cell inconsistencies are evaluated through the adaptive ratio vector, based on the analysis of cell current–voltage characteristics. In [19][5], a weighted RLS (WRLS) algorithm is employed in online parameters identification for SOP estimation, where a larger weight factor of an error gives rise to more impact on parameters adjustment. It should be noted that weight factors in a recent past window could exert an influence on the regression of the algorithm, and the optimisation of these weight factors is strongly related to the sampling rate and load profile. In [20][21][22], an optimal forgetting factor RLS (FFRLS) algorithm is implemented to determine model parameters by minimizing the accumulated squared error and updating progressively with data collections. A proper forgetting factor could effectively provide more impact of recent data than past data on the fine-tuning of model parameters, thereby acquiring better tracking ability and numerical stability. In [16], an adaptive forgetting factor least-square (AFFLS) algorithm is proposed to capture parameters variation in estimation of SOC and SOP, where the adaptive forgetting factor is designed to be current-dependent to compensate for the nonlinear correlation between charge transfer resistance and current. In [23], an improved AFFLS algorithm is developed to achieve preferable performance in processing fluctuated data, while simplifying preliminary experimental analysis and data fitting, thereby enhancing its operability in online SOP estimation. In [24], the authors emphasize that the unexpected sensing noises in current and voltage signals may cause biased parameters identification and further affect SOC and SOP estimation accuracy. Therefore, an adaptive forgetting factor recursive total least square (AFFRTLS) algorithm is proposed to suppress the current and voltage corruptions by finding out the optimal solution with the minimum perturbation on a battery system. According to the experimental results, the proposed algorithm presents a SOC error of less than 2.7% against sensing noises, while the error is up to 5% using a FFRLS algorithm.
The KF family is another important recursive method that shows an advantage in either the joint or dual estimation of both model parameters and state variables of a battery system [25]. In a joint estimation strategy, the state vector of a battery system is augmented to include model parameters, one KF is used to estimate both battery parameters and states to improve the computational efficiency. In [26], battery OCV is treated as a state variable instead of SOC in this algorithm to provide the basis for SOP estimation, and an offline calibrated curve, in relation to the rate of OCV change per ampere-hour, is employed to achieve close-loop compensation. However, the initial values of the KF are required to be well chosen to ensure convergence. In [27], to jointly estimate battery model parameters and state variables, while considering current dependency on charge transfer resistance, the fully-polarised internal resistance is calibrated at various current amplitudes and treated as an observation in an unscented KF (UKF). By doing so, it enables a viable way to capture the current effect for online SOP estimation while avoiding constructing a BVE-based highly nonlinear model. In [28], a fractional KF algorithm is employed to realise the joint estimation of battery states and model parameters of a simplified fractional-order model, where the state covariance prediction is associated with the previous state in a memory horizon, instead of only the last one.
As for a dual estimation strategy, two KFs are placed in parallel to act as state and weight filters, to concurrently share the derived information of state variables and model parameters with each other [25]. Although the dual strategy demonstrates a relatively complex structure, it could avoid large matrix operations in a joint estimation strategy and, thus, relieve the computational burden. In [29][30], both battery model parameterization and online SOC estimation are implemented using a dual EKF (DEKF) algorithm. In [29], the proposed DEKF algorithm employs battery polarisation current, flowing through the charge transfer resistance of a 1-RC model as the state vector, and incorporates battery OCV into the parameter vector. As a benefit, the partial derivative in DEKF algorithm can be simplified. According to the experimental validations on a new and aged cell, the estimated voltage error can be restricted within 0.03 V against noise. In [30], a pseudo-random binary sequence (PRBS) is applied to recalibrate parameters by exciting batteries during a relaxation, which delivers a reliable prior knowledge to an EKF for subsequent online adaptation. According to the validations, the proposed hybrid parameters identification method exhibits higher accuracy and faster convergence speed than EKF algorithm without prior knowledge, indicating the significance of prior knowledge for regression-based algorithms. In [31], cell parameters and SOCs in a battery pack are concurrently estimated through a dual adaptive EKF (DAEKF) algorithm, which has a stronger convergence capability than EKF algorithm by regressing noise covariance iteratively. Then, the weakest cell will be identified for pack-level SOP estimation.
Additionally, the extremum seeking algorithm, as another typical recursive method, is employed in [8] to characterize model parameters for instantaneous SOP estimation, where a sinusoidal current signal is imposed on a battery system to generate a cost function. The estimated model parameters will converge to true values, as long as the cost function is approaching zero.
Non-recursive methods, such as optimisation algorithms, possess good accuracy and stability over recursive methods, especially for ECMs with complex structures and more parameters. However, these methods are generally computationally expensive and require processing batches of data simultaneously. In [14], the parameters of a 1-RC model, incorporating the be, are updated online at the interval of 10 s, through an optimal searching strategy. The basic idea is to select a reference parameter set, among a number of the randomly generated parameter sets, at each iteration, according to the accumulated squared voltage error [32]. In [33], a particle swarm optimisation (PSO) algorithm is employed in online parameters identification for SOP estimation. Due to slow-varying characteristic of model parameters, it is not necessary to implement PSO algorithm at each sampling time, thereby alleviating its computational effort. From the experiments on nine different cells, PSO algorithm outperforms RLS algorithm in battery voltage and SOC estimation.

2.3. Improvements on SOP Estimation Algorithms

2.3.1. Long-Term SOP Estimation

Model parameter variation needs to be considered in a lengthy prediction window to maintain model accuracy in SOP estimation against varying SOC. This will lead to the increased computational complexity in solving peak currents online at CC, CV, and CCCV modes.
In [34], the ohmic resistance of a 1-RC model is predicted forward in a prediction window using the first-order Taylor series expansion. As a result, the mathematical expression of the peak discharge current becomes a second-order polynomial, and an optimal searching algorithm is designed to seek peak discharge current, while peak charge current estimation is not involved. To further engage all model parameters in forward prediction, the same authors employed a genetic algorithm (GA) to work out the peak discharge and charge currents from a highly nonlinear function; additionally, the effects of erroneous SOC and battery aging on SOP estimation were systematically analysed [35]. In [36], the authors stated that the first-order Taylor series expansion may yield unrealistic estimations of model parameters (e.g., negative values) at the end of a prediction window. To tackle this issue, a voltage, limited by extrapolation of resistances and OCV (VLERO) method, is proposed by extrapolating the model parameters on a slope connected between the present and minimum values over a whole SOC range. Moreover, a multistep model predictive iterative (MMPI) algorithm was derived to achieve SOP estimation in high accuracy, which can be separated into an inner and outer stage. In the inner stage, a prediction window is segmented into several subintervals to capture the variation trend of polarisation voltage in great detail, based on the model parameters estimated at each end of the subinterval. A root-searching algorithm is performed in the outer stage to find out the exact peak current from a complex function. The proposed MMPI algorithm is validated under dynamic profiles at low temperature, which shows a much preferable performance to a conventional long-term SOP estimation at the CC mode.

2.3.2. Optimisation Control-Based SOP Estimation

SOP estimation can also be converted into an optimisation problem using control theory. In [37], a dynamic matrix control (DMC) algorithm, developed from the model predictive control (MPC) theory, is applied in SOP estimation. Battery terminal voltage is formulated as a linear combination of the weighted sum of current changes in a recent past window. Thus, the proposed algorithm optimises the power flow through a tuning load current to make a battery reach its cut-off voltage at the end of a prediction window. In [38], an economic nonlinear MPC algorithm is employed in SOP estimation, under the constraints of voltage, current, SOC, and temperature. Compared with conventional MPC and DMC algorithms, mainly designed for tracking purpose, the proposed algorithm could avoid laborious weight-tuning work and achieve improved close-loop performance, especially targeting the nonlinear system. Besides, the effects of temperature, the length of a prediction window and model accuracy on SOP estimation are quantitatively explored. The experimental results show the error of peak power estimation is less than 0.2%.
Fuzzy logic control theory can be also applied in SOP estimation. In [39][40], a fuzzy logic controller is designed to prevent batteries from breaching the pre-set constraints and guarantee the safe operation of lithium-ion batteries. SOP estimation outcomes, provided by a MPC algorithm at CC or CCCV modes, will be delivered to a fuzzy logic controller, which divides the safe operating area into an inner and outer region. Once battery terminal voltage or current enters into the outer region at a sudden load change, the fuzzy logic controller will commence the adaption process before a battery approaches its pre-set constraints, where the correction coefficient depends on battery voltage and current, along with their variation rates.

2.3.3. SOP-Related Multi-State Co-Estimation

Generally, SOC, reflecting the ratio of battery remaining capacity to its rated capacity, is regarded as the indispensable precondition for SOP estimation. Many joint SOC and SOP estimation methods have been reported in the literature. With in-depth studies on lithium-ion batteries, it was found that the multi-physics coupling effect among various battery states could impose a significant impact on the estimation performance of every single state. Therefore, SOP-related, multi-state estimation becomes a promising way to facilitate SOP estimation in practice and has been a research hotspot in recent years. The relevant methods will be reviewed, with a special emphasis on the contributions of SOE and SOH to SOP estimation.
As one of the most fundamental battery states of lithium-ion batteries, SOE describes the ratio of battery remaining energy to its rated energy, which is closely related to EV remaining driving range estimation. From an energy management standpoint, it could also offer batteries a constraint in SOP estimation to prevent them from falling into energy poverty quickly. In [41], SOE completely supersedes SOC to act as a constraint in SOP estimation. According to the authors, SOE limit could have a higher impact on SOP estimation than SOC limits, since battery internal energy dissipation in a prediction window cannot be reflected by SOC, from a charge accumulation perspective. In [7], multi-state estimation algorithms, including SOC, SOE, and SOP, are presented, based on a 1-RC model with hysteresis. Although SOE is a state variable in battery state-space model, it does not participate in the model observation equation, which is estimated in an open-loop fashion. However, the above two methods ideally assume battery terminal voltage to be constant in a prediction window, which is practically untrue and, thereby, provides over-optimistic estimation results. Moreover, it is a necessity to experimentally investigate the battery operating ranges that SOC and SOE limits would, respectively, come into effect in SOP estimation, before completely replacing SOC limit with SOE limit.
SOH is a measure of the fade of battery capacity or increase of battery internal resistance, compared with a fresh battery. It can be calculated as a ratio of the maximum battery capacity at its current state to its rated capacity or the ratio of the internal resistance at its current state to the internal resistance at a fresh battery. Unlike the contribution of SOE, SOH estimation mainly dedicates to model parameters recalibration against battery degradation, thereby improving the SOC and SOP estimation accuracy over battery lifetime. In [42], a multi-state estimation framework of SOC, SOH, and instantaneous SOP was developed for lithium-ion batteries in EVs. A DP model, with offline characterized SOC- and temperature-dependent model parameters, was employed in SOC estimation, while the estimations of SOH and instantaneous SOP shared a Rint model. The SOH estimation in this research only helps recalibrate the available battery capacity, battery aging effect on the other model parameters is not taken into consideration, which would affect SOC estimation in the long run. Further, the employment of two ECMs with different structure and parameters reduces the applicability in practice. Another multi-state estimation framework of SOC, SOH, and SOP is proposed in [43], where SOH will be updated quarterly or semi-annually, based on the charge accumulation between two separate SOCs. Thus, the degradation trend of available battery capacity can be captured, yielding the improved performance of SOP estimation at the CCCV mode. A similar SOH update mechanism is also applied in [44]. Besides, the authors discovered that the OCV–SOC curve barely drifts above 62.5% SOC over a whole battery lifetime in EVs (i.e., 80–100% SOH), with a voltage deviation of less than 0.005 V. In this regard, two separate SOCs will be selected, in a range above 62.5% SOC. To further illustrate the correlation among SOC, SOH, and SOP, an enhanced multi-state estimation hierarchy is proposed in [45], where SOC estimation provides the basis for SOH and SOP estimation. SOH estimation is at the mid-layer, which can help to improve model robustness for SOP estimation and recalibrate SOC estimation against battery aging. The top layer of the hierarchy is a SOP estimation that could attain high reliability, benefiting from the precise knowledge of both SOC and SOH. Three length-varying rolling windows are designed for model parameters identification, SOH estimation, and SOP prediction, respectively. First, a modified moving horizon estimation (MHE) algorithm, with enhanced numerical stability and fault tolerance, is employed in SOC estimation. Second, periodical updates of model parameters and SOH will further lead to improved accuracy in SOC estimations. By doing so, a newly defined current limit, focusing on an increased heat generation on ohmic resistance in an aged battery, can be introduced into SOP estimation for safety consideration. The experimental results validate the effectiveness of the proposed multi-state estimation for SOC, SOH, and SOP of cells at different aging statuses. In [46], the multi-state estimation algorithm, with respect to SOC, SOH, and SOP, was proposed, primarily based on the mixed SOH estimation strategy. In this proposed algorithm, a 3-RC model was constructed, with parameters calibrated on a battery at different aging states, while an interacting multiple model strategy is applied to evaluate the respective mode probabilities, based on the corresponding likelihood functions. According to the aging states of the pre-defined models and their mode probabilities, the first SOH candidate can be generated. In addition, the online identified ohmic resistance is treated as the second candidate of SOH. The overall SOH estimation can be determined by taking a weighted average between two candidates, thereby achieving a smooth mode transition and benefiting from more stable SOP estimation.

2.3.4. Machine Learning-Based SOP Estimation

Machine learning algorithms exhibit outstanding performance in nonlinear system modelling, some of them with simple structure, and few parameters have been attempted in SOP estimation for the improved accuracy, while keeping a relatively low computational expense. In [47], a self-learning estimation algorithm was proposed for SOP estimation, based on an adaptive neuro-fuzzy inference system (ANFIS). The proposed ANFIS treats the current amplitude, charge accumulation, SOC, temperature, and time-averaged voltage during a pulse as the system inputs, while the system output is the battery terminal voltage at the end of a prediction window. A two-step hybrid learning method is employed in ANFIS training. In the first step, a forward pass is performed with fixed premise parameters to generate the corresponding output error. Then, a gradient descent-based back pass is carried out in the second step to fine-tune the premise parameters. Finally, the peak discharge and charge current/power is determined by iteratively running the system, and the estimation will gradually approach the peak value through a bisection method. In [48], a model-based extreme learning machine (ELM) algorithm was derived to predict battery future power capability, voltage, and temperature against varying SOC and temperature. The proposed ELM algorithm replaces original active functions in conventional ELMs with a set of sub-models. Each of these sub-models contains a 1-RC model and thermal model, with randomly selected initial SOC and model parameters in a reasonable range to reproduce battery electrical and electrothermal dynamics. As an advantage, little priori knowledge of a battery is required, thereby facilitating the robustness of the algorithm. According to the experimental results at 5 °C, 25 °C, and 45 °C, the proposed algorithm performs satisfyingly over the generic RLS algorithm.

2.3.5. Pack-Level SOP Estimation

EV battery packs are made up of numerous cells connected in series or parallel (or combination of both) to meet specific power and energy requirements. Thus, pack-level SOP estimation appears to be subjected to all cell-level constraints. The fundamental idea of the conventional pack-level SOP estimation is to predict the SOP of a single cell and then scale it up to the whole battery pack. Nevertheless, cell inconsistencies are inevitable in the process of manufacturing and usage. Neglecting cell inconsistencies in a battery pack may yield unreliable SOP estimation outcomes. As a result, it could aggravate battery aging behaviour and even risk batteries in potential safety issues. Generally, serial or parallel connections are two common configurations to make a battery pack [49].
For a battery pack comprising of only serial-connected cells, pack-level SOP depends on the representative cell that first reaches any of the pre-set constraints [50]. A straightforward strategy to determine the representative cell in a battery pack is proposed in [6][51] by comparing the peak cell currents in a prediction window. However, this strategy requires a large memory from BMSs to construct ECMs for each single cell and store the corresponding parameters. Also, working out all the peak cell currents would produce a heavy computational burden on a microprocessor with limited computation capability. To facilitate the applicability and efficiency of pack-level SOP estimation, an improved cell-selection strategy was devised in [31], based on the extraction of cell inherent features (e.g., OCV and ohmic resistance), which enables to pick the representative cell before implementing the peak current estimation. Although laborious computational effort on calculating peak cell currents can be avoided, it still requires cell-level modelling and the corresponding estimators for cell parameter identification. In light of this, a comprehensive model is constructed to describe dynamic behaviours of a battery pack, while cell-to-cell differences are reflected by a set of proportional factors that replace cell inherent features (e.g., cell capacity and ohmic resistance) in representative cell selection [14][18]. Afterwards, the peak discharge and charge currents of the representative cell cooperate with the average cell voltage to generate pack-level SOP. As an advantage, it only needs one estimator to suffice for the parameter identification at a pack level that further saves computational resources.
The aforementioned SOP estimation strategies are readily applicable to a serial-connected battery pack, which do not consider the presence of parallel-connected cells. Unlike serial-connected battery packs that share an identical current, dynamic current distribution would be the most intractable problem for SOP estimation of a battery pack in a parallel-connected structure. Concerning this, an application-oriented SOP estimation strategy was proposed in [52] for a battery pack constituting parallel-connected strings with a number of cells connected in series on each string. Firstly, a generalised state-space representation of a n-RC model is constructed to describe battery internal dynamics, which treats either cell voltage or string current as a system output, with the pack current as a system input. This makes the complicated system much easier to monitor. Secondly, the SOP estimation is formulated as an optimisation problem that not only searches the cell index hitting the pre-set constraint but also determine the exact time instance, since a possible non-monotonic variation of cell voltage may occur, in spite of operating at a constant current. Further, cell SOPs at the beginning and end of a prediction window will be tried before solving the optimisation problem to reduce the computational effort.

References

  1. Sun, F.; Xiong, R.; He, H.; Li, W.; Aussems, J.E.E. Model-Based Dynamic Multi-Parameter Method for Peak Power Estimation of Lithium–Ion Batteries. Appl. Energy 2012, 96, 378–386.
  2. Sun, F.; Xiong, R.; He, H. Estimation of State-of-Charge and State-of-Power Capability of Lithium-Ion Battery Considering Varying Health Conditions. J. Power Sources 2014, 259, 166–176, doi:10.1016/j.jpowsour.2014.02.095.
  3. Wang, S.; Verbrugge, M.; Wang, J.S.; Liu, P. Multi-Parameter Battery State Estimator Based on the Adaptive and Direct Solu-tion of the Governing Differential Equations. J. Power Sources 2011, 196, 8735–8741.
  4. Pei, L.; Zhu, C.; Wang, T.; Lu, R.; Chan, C.C. Online Peak Power Prediction Based on a Parameter and State Estimator for Lithium-Ion Batteries in Electric Vehicles. Energy 2014, 66, 766–778, doi:10.1016/j.energy.2014.02.009.
  5. Wang, S.; Verbrugge, M.; Wang, J.S.; Liu, P. Power Prediction from a Battery State Estimator That Incorporates Diffusion Resistance. J. Power Sources 2012, 214, 399–406.
  6. Hu, X.; Xiong, R.; Egardt, B. Model-Based Dynamic Power Assessment of Lithium-Ion Batteries Considering Different Operating Conditions. IEEE Trans. Ind. Inf. 2014, 10, 1948–1959.
  7. Wang, Y.; Pan, R.; Liu, C.; Chen, Z.; Ling, Q. Power Capability Evaluation for Lithium Iron Phosphate Batteries Based on Multi-Parameter Constraints Estimation. J. Power Sources 2018, 374, 12–23.
  8. Wei, C.; Benosman, M. Extremum Seeking-Based Parameter Identification for State-of-Power Prediction of Lithium-Ion Batteries. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), IEEE, Birmingham, UK, 20–23 November 2016; pp. 67–72.
  9. Xiang, S.; Hu, G.; Huang, R.; Guo, F.; Zhou, P. Lithium-Ion Battery Online Rapid State-of-Power Estimation under Multiple Constraints. Energies 2018, 11, 283.
  10. Hu, X.; Li, S.; Peng, H. A Comparative Study of Equivalent Circuit Models for Li-Ion Batteries. J. Power Sources 2012, 198, 359–367.
  11. Dong, G.; Wei, J.; Chen, Z. Kalman Filter for Onboard State of Charge Estimation and Peak Power Capability Analysis of Lithium-Ion Batteries. J. Power Sources 2016, 328, 615–626.
  12. Feng, T.; Yang, L.; Zhao, X.; Zhang, H.; Qiang, J. Online Identification of Lithium-Ion Battery Parameters Based on an Improved Equivalent-Circuit Model and Its Implementation on Battery State-of-Power Prediction. J. Power Sources 2015, 281, 192–203.
  13. Jiang, J.; Liu, S.; Ma, Z.; Wang, L.Y.; Wu, K. Butler-Volmer Equation-Based Model and Its Implementation on State of Power Prediction of High-Power Lithium Titanate Batteries Considering Temperature Effects. Energy 2016, 117, 58–72.
  14. Waag, W.; Fleischer, C.; Sauer, D.U. Adaptive On-Line Prediction of the Available Power of Lithium-Ion Batteries. J. Power Sources 2013, 242, 548–559.
  15. Tang, X.; Wang, Y.; Yao, K.; He, Z.; Gao, F. Model Migration Based Battery Power Capability Evaluation Considering Uncertainties of Temperature and Aging. J. Power Sources 2019, 440, 227141.
  16. Yang, L.; Cai, Y.; Yang, Y.; Deng, Z. Supervisory Long-Term Prediction of State of Available Power for Lithium-Ion Batteries in Electric Vehicles. Appl. Energy 2020, 257, 114006.
  17. Gao, W.; Zou, Y.; Sun, F.; Hu, X.; Yu, Y.; Feng, S. Data Pieces-Based Parameter Identification for Lithium-Ion Battery. J. Power Sources 2016, 328, 174–184.
  18. Jiang, B.; Dai, H.; Wei, X.; Zhu, L.; Sun, Z. Online Reliable Peak Charge/Discharge Power Estimation of Series-Connected Lithium-Ion Battery Packs. Energies 2017, 10, 390.
  19. Wang, S.; Verbrugge, M.; Wang, J.S.; Liu, P. Multi-Parameter Battery State Estimator Based on the Adaptive and Direct Solution of the Governing Differential Equations. J. Power Sources 2011, 196, 8735–8741.
  20. Xiong, R.; He, H.; Sun, F.; Liu, X.; Liu, Z. Model-Based State of Charge and Peak Power Capability Joint Estimation of Lithium-Ion Battery in Plug-in Hybrid Electric Vehicles. J. Power Sources 2013, 229, 159–169.
  21. Xiong, R.; He, H.; Sun, F.; Zhao, K. Online Estimation of Peak Power Capability of Li-Ion Batteries in Electric Vehicles by a Hardware-in-Loop Approach. Energies 2012, 5, 1455–1469.
  22. Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476.
  23. Li, B.; Wang, S.; Fernandez, C.; Yu, C.; Xia, L.; Fan, Y. A Linear Recursive State of Power Estimation Method Based on Fusion Model of Voltage and State of Charge Limitations. J. Energy Storage 2021, 40, 102583.
  24. Wei, Z.; Zhao, J.; Xiong, R.; Dong, G.; Pou, J.; Tseng, K.J. Online Estimation of Power Capacity With Noise Effect Attenuation for Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2019, 66, 5724–5735.
  25. Plett, G.L. Dual and Joint EKF for Simultaneous SOC and SOH Estimation. In Proceedings of the 21st Electric Vehicle Symposium (EVS21), Monte Carlo, Monaco, 2–6 April 2005; pp. 1–12.
  26. Juang, L.W.; Kollmeyer, P.J.; Jahns, T.M.; Lorenz, R.D. Implementation of Online Battery State-of-Power and State-of-Function Estimation in Electric Vehicle Applications. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Raleigh, NC, USA, 15–20 September 2012; pp. 1819–1826.
  27. Zhang, W.; Wang, L.; Wang, L.; Liao, C.; Zhang, Y. Joint State-of-Charge and State-of-Available-Power Estimation Based on the Online Parameter Identification of Lithium-Ion Battery Model. IEEE Trans. Ind. Electron. 2021, 1.
  28. Li, X.; Sun, J.; Hu, Z.; Lu, R.; Zhu, C.; Wu, G. A New Method of State of Peak Power Capability Prediction for Li-Ion Battery. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), IEEE, Montreal, QC, Canada, 19–22 October 2015; pp. 1–5.
  29. Pei, L.; Zhu, C.; Wang, T.; Lu, R.; Chan, C.C. Online Peak Power Prediction Based on a Parameter and State Estimator for Lithium-Ion Batteries in Electric Vehicles. Energy 2014, 66, 766–778.
  30. Nejad, S.; Gladwin, D.T. Online Battery State of Power Prediction Using PRBS and Extended Kalman Filter. IEEE Trans. Ind. Electron. 2020, 67, 3747–3755.
  31. Zhou, Z.; Kang, Y.; Shang, Y.; Cui, N.; Zhang, C.; Duan, B. Peak Power Prediction for Series-Connected LiNCM Battery Pack Based on Representative Cells. J. Clean. Prod. 2019, 230, 1061–1073.
  32. Waag, W.; Fleischer, C.; Sauer, D.U. On-Line Estimation of Lithium-Ion Battery Impedance Parameters Using a Novel Varied-Parameters Approach. J. Power Sources 2013, 237, 260–269.
  33. Zhang, X.; Wang, Y.; Wu, J.; Chen, Z. A Novel Method for Lithium-Ion Battery State of Energy and State of Power Estimation Based on Multi-Time-Scale Filter. Appl. Energy 2018, 216, 442–451.
  34. Chen, Z.; Lu, J.; Yang, Y.; Xiong, R. Online Estimation of State of Power for Lithium-Ion Battery Considering the Battery Aging. In Proceedings of the 2017 Chinese Automation Congress (CAC), IEEE, Jinan, China, 20–22 October 2017; pp. 3112–3116.
  35. Lu, J.; Chen, Z.; Yang, Y.; Ming, L.V. Online Estimation of State of Power for Lithium-Ion Batteries in Electric Vehicles Using Genetic Algorithm. IEEE Access 2018, 6, 20868–20880.
  36. Malysz, P.; Ye, J.; Gu, R.; Yang, H.; Emadi, A. Battery State-of-Power Peak Current Calculation and Verification Using an Asymmetric Parameter Equivalent Circuit Model. IEEE Trans. Veh. Technol. 2016, 65, 11.
  37. Wang, L.; Cheng, Y.; Zou, J. Battery Available Power Prediction of Hybrid Electric Vehicle Based on Improved Dynamic Matrix Control Algorithms. J. Power Sources 2014, 261, 337–347.
  38. Zou, C.; Klintberg, A.; Wei, Z.; Fridholm, B.; Wik, T.; Egardt, B. Power Capability Prediction for Lithium-Ion Batteries Using Economic Nonlinear Model Predictive Control. J. Power Sources 2018, 396, 580–589.
  39. Esfandyari, M.J.; Hairi Yazdi, M.R.; Esfahanian, V.; Masih-Tehrani, M.; Nehzati, H.; Shekoofa, O. A Hybrid Model Predictive and Fuzzy Logic Based Control Method for State of Power Estimation of Series-Connected Lithium-Ion Batteries in HEVs. J. Energy Storage 2019, 24, 100758.
  40. Esfandyari, M.J.; Esfahanian, V.; Hairi Yazdi, M.R.; Nehzati, H.; Shekoofa, O. A New Approach to Consider the Influence of Aging State on Lithium-Ion Battery State of Power Estimation for Hybrid Electric Vehicle. Energy 2019, 176, 505–520.
  41. Zhang, W.; Shi, W.; Ma, Z. Adaptive Unscented Kalman Filter Based State of Energy and Power Capability Estimation Approach for Lithium-Ion Battery. J. Power Sources 2015, 289, 50–62.
  42. Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The Co-Estimation of State of Charge, State of Health, and State of Function for Lithium-Ion Batteries in Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 67, 92–103.
  43. Zhang, T.; Guo, N.; Sun, X.; Fan, J.; Yang, N.; Song, J.; Zou, Y. A Systematic Framework for State of Charge, State of Health and State of Power Co-Estimation of Lithium-Ion Battery in Electric Vehicles. Sustainability 2021, 13, 5166.
  44. Shu, X.; Li, G.; Shen, J.; Lei, Z.; Chen, Z.; Liu, Y. An Adaptive Multi-State Estimation Algorithm for Lithium-Ion Batteries Incorporating Temperature Compensation. Energy 2020, 207, 118262.
  45. Hu, X.; Jiang, H.; Feng, F.; Liu, B. An Enhanced Multi-State Estimation Hierarchy for Advanced Lithium-Ion Battery Management. Appl. Energy 2020, 257, 114019.
  46. Rahimifard, S.; Ahmed, R.; Habibi, S. Interacting Multiple Model Strategy for Electric Vehicle Batteries State of Charge/Health/ Power Estimation. IEEE Access 2021, 9, 109875–109888.
  47. Fleischer, C.; Waag, W.; Bai, Z.; Sauer, D.U. Self-Learning State-of-Available-Power Prediction for Lithium-Ion Batteries in Electrical Vehicles. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, South Korea, 9–12 October 2012; pp. 370–375.
  48. Tang, X.; Yao, K.; Liu, B.; Hu, W.; Gao, F. Long-Term Battery Voltage, Power, and Surface Temperature Prediction Using a Model-Based Extreme Learning Machine. Energies 2018, 11, 86.
  49. Roşca, B.; Wilkins, S.; Jacob, J.; Hoedemaekers, E.; Van Den Hoek, S. Predictive Model Based Battery Constraints for Electric Motor Control within EV Powertrains. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), IEEE, Florence, Italy, 17–19 December 2014; pp. 1–8.
  50. Li, X.; Xu, J.; Hong, J.; Tian, J.; Tian, Y. State of Energy Estimation for a Series-Connected Lithium-Ion Battery Pack Based on an Adaptive Weighted Strategy. Energy 2021, 214, 118858.
  51. Zhang, C.; Sharkh, S.M. Estimation of Real-Time Peak Power Capability of a Traction Battery Pack Used in an HEV. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, IEEE, Chengdu, China, 28–31 March 2010; pp. 1–6.
  52. Han, W.; Altaf, F.; Zou, C.; Wik, T. State of Power Prediction for Battery Systems with Parallel-Connected Units. IEEE Trans. Transp. Electrif. 2021, 1.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback