Autonomous vehicles are becoming increasingly prevalent on roadways around the world; a study conducted in 2020 by Mordor Intelligence [1] reports that “the autonomous (driverless) car market was valued at USD 20.97 billion in 2020” and is projected to increase by 22.75%, to USD 61.93 billion by 2026. While consistent and significant technological advancements are being made in related fields, confidence in autonomous systems for use on roadways is declining. AAA reported in 2018 [2] that 73% of adults in the United States claim to be “too afraid” of allowing a vehicle to autonomously control itself—this is an increase of 10% from a similar study conducted one year prior.

Eliminating the human element of vehicular control, of course, subsequently eliminates the risk of traffic collisions resulting from human error. Furthermore, the occupants of autonomous vehicles are free to spend travel time recreationally or occupationally; this is especially beneficial considering the increasing congestion on roadways within major settlements, alongside a growing world population.

In the event that most, if not all, vehicles on roadways possess fully autonomous capabilities, it would be possible for a system to be implemented wherein these vehicles communicate with one another by sharing information on hazards ahead and manoeuvres they wish to perform. The resulting improvements to travel efficiency would likely have a cascading effect through iterative increases to speed limits.

Additionally, the Mobility-as-a-Service (MAAS) market is likely to see an increase in potential as autonomous vehicles acquire mass-adoption. Fully autonomous MAAS would hypothetically enable individuals to, rather than owning a personal vehicle, lease a vehicle for each journey they embark upon, similar to how companies such as Uber and Lyft currently operate, however in this case, without the need for a driver. Alternatively, those who do opt to purchase their own autonomous vehicle would have the opportunity to lease the vehicle out when not in use, providing an additional stream of income.

In an autonomous driving system, the safety of vehicle occupants, as well as individuals in the surrounding environment, should be guaranteed. One recent study conducted by Najada and Mahgoub [3] revealed that approximately 80% of casualties resulting from vehicle-related accidents were pedestrians.

The safety of vehicle occupants and pedestrians can be achieved through collision avoidance warning systems (CAWS). A key component of CAWS is vehicular situational awareness, which can be facilitated through the use of different types of sensors. These sensors gather data pertaining to the vehicle’s surroundings, which can then be processed, with useful information being extracted. LiDAR, RADAR, and camera sensors are the three most prominent sensors currently in use.

In this paper, the use of cameras and computer vision in the scope of pedestrian detection and classification, touching on methods by which LiDAR can be used to improve such a system through sensor fusion are investigated. Here, pedestrian detection can be defined as the process of determining whether an image, generally a frame extracted from a video sequence, contains pedestrian instances. A successful system should be able to leverage computer vision technologies in order to extract the specific locations of any pedestrians in the frame [4], the results of which are usually in the form of bounding boxes encapsulating individual pedestrian instances.

Machine learning models are generally bespoke, designed with a specific use-case in mind. While the performance of these models can be exceptional, the training process requires a substantial amount of labelled data, which can be incredibly time-consuming. ImageNet [5] is an example of such a dataset, consisting of over 14 million images across thousands of classes. Models trained using ImageNet may be exceptional at differentiating between a wide variety of classes, however, applying such a model to a more specific use-case would likely result in a significant loss of performance. Hence, the motivation to make use of transfer learning in this paper to reduce computer complexity and enable the transfer of learning from a previously trained model.

Identifying and localizing pedestrian shapes in images has, perhaps, been one of the greater challenges facing computer vision researchers over the past decades [6], largely due to the variable appearance of the human body and variations in illumination, occlusion, and poses [7]. Recently, however, with the advent of increasingly powerful and compact hardware, pedestrian detection systems have taken great strides in terms of efficiency and accuracy ^[8][9][10][8,9,10].

There are two primary methods of achieving pedestrian classification through computer vision: deep learning [11] and machine learning [12] based methods; both approaches follow similar computational pipelines. First, candidate regions must be identified—this can be achieved through the application of either a sliding window, or some more complex region proposal algorithm ^[13][14][13,14]. Once candidate regions are identified, feature extraction is applied to these regions to obtain an accurate classification on the basis of subsequent classification algorithms.

In 1999, Lowe proposed a visual recognition system [15] which makes use of local features which are scale-invariant and partially invariant to changes in illumination. This publication is indicative of researchers’ shift in focus at the time, from attempts to reconstruct objects as three-dimensional objects [16], to feature-based object recognition. Soon after, Viola and Jones published a real-time facial recognition framework [17] in the form of a binary classifier consisting of numerous, weaker, classifiers which are trained using Adaboost [18]. Viola and Jones later went on to propose a pedestrian detection algorithm which used motion and appearance information in order to detect a moving person [19]. Dalal and Triggs expanded this work [20] and proposed the use of Histogram of Oriented Gradients (HOG) as a feature extractor, with the resulting HOG features being fed into a linear Support-Vector Machine (SVM) [21] classifier. This HOG-SVM combination is capable of differentiating between regions which contain pedestrians and those which do not. The resulting reduction in the number of false positives was over an order of magnitude, compared to the best performing Haar wavelet detector at the time [22]. While HOG-SVM offers exceptional performance in classification tasks, it fails to achieve a low mean average precision [23].

In 2008, Felzenswalb et al. utilised the HOG-based detector in their multiscale Deformable Part Model (DPM) [24] which deconstructs objects into groups based on pictorial models [25]. The DPM was suggested to be state-of-the-art at the time, outperforming other methods of object detection, such as template matching.

McCulloch and Pitts first proposed the McCulloch-Pitts (MCP) model in 1943 [26], which is widely accepted as the genesis of Artificial Neural Networks. In 1980, Fukushima introduced Neocognitron, a hierarchical, multilayer Artificial Neural Network which was designed for use in handwritten character recognition and similar pattern recognition tasks. The model consisted of several pooling and convolutional layers, which provided the ability to learn how to identify visual patterns in images. LeCun et al. inspired from Neocognitron proposed the concept of Convolutional Neural Networks (CNNs) which utilize error gradient, yielding impressive results in a range of pattern recognition applications ^[27][28][29][27,28,29].

CNNs [30] are perhaps the most prevalent application of deep learning for computer vision tasks, as they have proven to be exceptionally well-suited for tackling object detection problems, in part due to their ability to extract discriminative features. CNNs are composed of three different types of neural layers: convolutional layers, pooling layers, and fully connected layers. In the context of computer vision tasks, Yosinski et al. [31] deduced that the lower layers (i.e., convolutional and pooling) act in a similar manner to conventional computer vision-based feature extractors such as edge detectors, while the final, fully connected layers, are more task-specific. In [32] authors showed that CNNs outperformed both HOG descriptor and Haar-classifier.

As discussed in earlier sections, deep learning and machine learning models require significant volumes of data for use during training. This was identified in 2001 in a research report published by Gartner [33], which alluded to the impending surge of big data. An on-board pedestrian detection system is proposed in [34] based on 2D and 3D cues. Just under a decade later, the ImageNet database was introduced by Deng et al. in 2009 [5]. Authors in [35] propose a dataset that includes challenges related to dense urban traffic, based on their dataset they propose a fusion framework for multi-object detection. The advent of larger datasets such as ImageNet required more capable deep learning models and, in 2012, Krizhevsky et al. introduced AlexNet [36]: a breakthrough in CNN architecture which makes use of the Rectified Linear Units (ReLU) activation function which provided a sixfold reduction in training time, compared to the TanH activation function which, at the time, was standard. Additionally, AlexNet has the capability of being trained across multiple GPUs simultaneously, which enabled more complex models to be produced and was a key enabler of the significant reduction in training time.

Transfer learning (TF) aims to provide a middle ground, where knowledge acquired from larger datasets can be used in conjunction with smaller, domain-specific, datasets in order to improve performance in subsequent domain-specific tasks. In this context, prior knowledge can be model weights or low-level image features which describe what is being classified such as edges, shapes, corners, pixel intensity, etc.

Therefore, the models produced in this work make use of transfer learning as it enhances the performance of the proposed CNN model with the VGG-16 architecture, proposed by Simonyan and Zisserman in 2014 [37]. The VGG-16 CNN model improves upon the work carried out for AlexNet by switching the 11 × 11 and 5 × 5 kernel-sized filters with two consecutive 3 × 3 filters in the first two convolutional layers.

2. CNNs for Pedestrian Recognition

R. Hecht-Nielsen [38] described neural networks as “a computing system made up of a number of simple, highly interconnected processing elements, which process information by their dynamic state response to external inputs”. The review presented here expands on the CNN and deep learning principle presented in ^[39][40][39,40] in the context of AlexNet [36]. They are modelled to mimic the human brain in order to recognize patterns. This is achieved through numerical input vectors that describe real-world information such as images and text, from which an output response can be generated. In the context of pedestrian classification, once a candidate region has been recognized through recognition techniques, it can be classified through the use of a neural network which allows for an appropriate response to be made by the vehicle. Convolutional Neural Networks (CNNs) mostly used in the computer vision field. CNNs are structured in a three-dimensional layers and processes information first through “convolution”, layer where small portions of data are analysed in order to create a “feature map”, before passing it to “pooling” layer. Here, each feature of the data set has its dimensionality reduced while retaining the most relevant information. This next section covers the related theory behind CNNs.

2.1. Single Layer Perceptrons

Perceptrons, sometimes referred to as “linear binary classifiers”, are a form of supervised classification algorithm that can be used to determine the classification of a given input. If neural networks are considered to be computational representations of the human brain the perceptrons act as individual neurons, which take the form of a single-layer neural network and consist of four key elements: input values, weight and bias, the net sum, and an activation function.

Input values are multidimensional vector values that are fed into the perceptron in order to be processed. The input values are multiplied by a weighting parameter, which is indicative of an individual input’s influence over the output value. The sum of the weighted input values is referred to as the “net sum” or “weighted sum”, and can be calculated with the following equation:

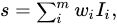
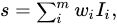
where s is the weighted sum, m is the number of inputs, w represents the weight for each input, and I represents the value of each input. Once a weighted sum has been calculated, it is then applied to the activation function, which normalizes it. In simple perceptron models, the activation is a step function. See Figure 1.

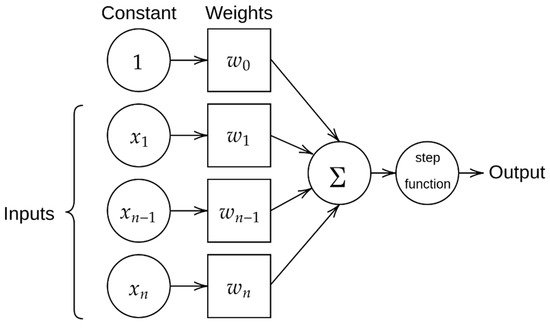
Figure 1. A simple perceptron model.

2.2. Multi-Layer Perceptrons

Multi-layer perceptron (MLP) is simply another way of referring to a neural network and consists of a collection of individual single-layer perceptrons (SLP) arranged into distinct “layers”. The most basic form of MLP consists of three layers: an input layer, output layer, hidden layer. The input and output layers serve the same purpose as in an SLP, the hidden layer is where most of the MLP’s computation is performed.

MLPs allow for non-linear classification, such as XOR functions, which is not possible with SLPs as they are not capable of modelling feature hierarchy. It is for that reason that SLPs generally only find use as building blocks for MLPs, which have been shown to approximate non-linear functions. Furthermore, SLPs simply use the step function as an activation function, whereas MLPs can use more complex activation functions which enable the classification of items into multiple labels as well as to provide probability-based prediction.

2.3. Activation Functions

Activation functions are mathematical equations that are not only used to determine the output of the individual perceptrons, but also the accuracy, computational efficiency during training, and the output of a deep learning model in its entirety. Additionally, selecting an appropriate activation function for the task the neural network is attempting to perform is crucial, as they have a significant influence over the network’s ability to converge and the speed at which it can converge. Examples of activation functions include the binary step, linear, sigmoid, TanH, rectified linear unit (ReLU), SoftMax and back propagation. ReLU is the most frequently used activation function due to their simplicity where positive values are treated linearly, and negative values are assigned a value of zero [41].

2.4. Hyperparameters

2.4.1. Hidden Layers and Units

Hidden layers are layers within a neural network that lie between the input and output layers. Increasing the number of hidden layers has the potential of increasing the accuracy of a model, however as more hidden layers are added, computational requirements will increase yet will yield diminishing returns on the error function.

Not having an adequate number of hidden layers on the other hand will result in poor generalization and unreliable predictions, so it is important to strike a balance in the selection of number of hidden layers.

2.4.2. Dropout

Dropout is a technique used during the training of a model in which certain nodes are deactivated so that it does not become overwhelmed with information, which can isolate nodes that may not be contributing to an improved error function, which in turn should produce a more efficient model.

2.4.3. Activation Function

Activation functions, which have been discussed earlier in this section, can be added to any point of a neural network and there is no limit to the amount that can be added which again results in the process of determining a suitable balance between the number of activation functions and the overall efficiency of the model.

2.4.4. Learning Rate

The learning rate determines the strength of changes made to weights during the process of backpropagation. A lower learning rate results in smoother convergence at the cost of an increase in training time and a higher learning rate will have opposing effects, which means the appropriate learning rate will be model-specific.

2.4.5. Epochs and Batch Size

The number of epochs represents the number of instances that the training dataset is fed into a neural network during the training process. Increasing the number of epochs will increase the accuracy to a certain extent, after which overfitting will start to occur, and training accuracy can decrease. Batch size controls the percentage of the dataset to be exposed to the network through each iteration (epoch) of the training process, which can reduce the over generalization of the model.

2.4.6. Optimisation Algorithm

Optimisation algorithms are those that attempt to minimize the error function of a model. There are two subcategories of optimization algorithms: “first-order” (e.g., gradient descent), which adjust the loss function with respect to given parameters, and “second-order”, which use what is known as the ‘second order derivative’ or “Hessian” to adjust the loss function.

First order optimizations are easier to compute and require less computational time to converge reasonably well with larger data sets. Second order derivatives are only able to outperform first order optimizations when a second order derivative is known, otherwise they are more computationally intensive and take longer to execute.

2.4.7. Momentum

Momentum is the process of tracking changes made to a model and the direction of those changes, which can be used to influence subsequent changes so that they follow the same direction, towards a lower error function.