You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 1 by Frank Ohme and Version 2 by Nora Tang.
The detections of gravitational-wave (GW) signals from compact binary coalescence by ground-based detectors have opened up the era of GW astronomy. These observations provide opportunities to test Einstein’s general theory of relativity at the strong-field regime.
- gravitational waves
- compact binary systems
- tests of General Relativity
1. Introduction
The binary evolution in General Relativity (GR) is described differently than in Newtonian gravity (NG). In GR, the binary orbit shrinks due to the emission of energy: angular and linear momenta through gravitational waves (GWs) [1][2][3][4][1,2,3,4]. Whereas in NG, there is no concept of radiation reaction and the orbital period is constant over time. Even though Albert Einstein predicted the existence of GWs more than a century ago, their detection remained a puzzle due to their weak interaction with matter. The indirect evidence of GWs came from the decades-long observations of orbital decay of a binary pulsar by Russell Alan Hulse and Joseph Taylor [5][6][7][8][5,6,7,8]. They found that the observed orbital decay of the binary system, known as PSR B1913+16(PSR J1915+1606, or PSR 1913+16), due to the emission of GWs, is consistent with the predictions of GR. That is, the rate of decay of the orbital period (Porb) from observations dPorb/dt∼ 10^{-14} – 10^{-12} agreed to the GR predicted rate obtained from analytical calculations based on GR, leading the team to win the Physics Nobel Prize in 1993.
The direct detection of GWs had to wait until the LIGO detectors at Hanford, Washington, and Livingston, Louisiana, made their first detection of a binary merger on 14 September 2015 [9][10][11][12][13][14][15][16][17][9,10,11,12,13,14,15,16,17]. This discovery opened the era of GW astronomy, noting the first highly relativistic strong-field observation of GWs. Within the subsequent years of observation runs, the LIGO-Virgo collaborations announced the detection of more than fifty binary merger events [12][18][19][20][21][22][23][24][25][26][27][28][29][12,18,19,20,21,22,23,24,25,26,27,28,29].
2. History and Development
Among the many significant contributions to fundamental physics and astrophysics, GW observations test GR at the relativistic, strong-field regime. A set of testing GR analyses conducted by the LIGO-Virgo Scientific Collaboration (LVC) on the GW150914 event established that GW150914 is consistent with a binary black hole (BBH) signal described in GR [9].
This set of tests include consistency tests, parameterized tests, tests to confirm the non-dispersive nature of the radiation, and tests on the remnant properties. Consistency tests check for the agreement of observed data with the signal predicted from GR. Parameterized tests introduce model-agnostic parametric GR deviations in the waveform and constrain those from the data to put statistical bounds on these parameters. The list of the GW events was extended further with more binary merger detections by LIGO and Virgo detectors’ first, second, and third observation runs. All the tests applied on GW150914 were also performed on these events with appropriate modifications to the above-mentioned tests, including additional tests. Here we will go through them in detail.
The GW-based tests of GR on the BBH coalescence events detected by LIGO and Virgo until 1 October 2019 are available in Reference [30]. A generic binary system evolves from its early inspiral weak-field regime to a highly relativistic merger and then the final ringdown stage. In the case of BBHs in GR, the object formed after they merge (i.e., the merger remnant) is another black hole (BH). On the other hand, for non-BH binaries [31][32][31,32],1 the merger remnant is not necessarily a BH but could be another compact star depending upon the properties of the binary.
In a model agnostic way, there were four broad classes of tests conducted in Reference [30]. These tests aim to look at different regimes of binary evolution or to the full inspiral-merger-ringdown signals. The first set consists of the residual analysis and the inspiral-merger-ringdown consistency test. Both of these tests check the consistency of GR predictions with the observed data (as in the case of Reference [9]). The second category of tests is the parametrized tests for GW generation and propagation. Here one sets statistical bounds on the parametrized deviations from GR, assuming GR is the correct theory of gravity, employing GR waveform models with parametric deviations present. On the third category of tests, one looks for any violation of GR by analyzing the merger remnant properties. The GW polarization tests look for extra polarization modes present in the data and comprise the fourth set of tests. This analysis provides statistical evidence for alternative theories of gravity that predict vector and scalar polarization modes along with the tensor modes. An overview of these tests is provided in Figure 1.
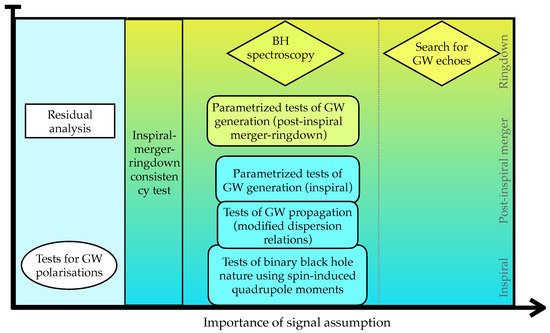
Figure 1. Outline of various tests of GR we discuss in this article. The x-axis denotes the increasing order of GR model assumptions that go into each analysis. The light-blue region on the left side contains the set of tests that require the least assumptions about the signal model. The gradient on the right part of the plot classifies the tests into inspiral, merger-ringdown regimes of the signal from bottom to top. Different shapes indicate different classes of tests: rectangle, rounded rectangle, ellipse, and diamond shapes correspond to consistency tests, parametrized tests, polarization tests, and tests for the merger remnant, respectively.
The probability of there being astrophysical origin of a candidate event plays an important role in determining whether that event is considered for the testing GR analyses or not. Usually, a higher threshold is assumed so that the events analyzed have higher chances of being of astrophysical origin. For instance, in Reference [30], events satisfying a false alarm rate (FAR) less than 10−3 per year are chosen to analyze. Once the set of events is chosen based on the detection significance, additional criteria are applied depending upon the strategies followed by each test. Bayesian formalism-based techniques are employed to get meaningful bounds from each test. The pipelines widely used for this purpose are, LALInference [33][48] available in the LIGO Scientific Collaboration’s algorithm library suite (LALSuite) [34][49], Bayeswave [35][36][50,51], parallel bilby (pBilby) [37][38][39][52,53,54], PYRING [40][41][55,56] and Bantam [42][57]. Reference [30] demonstrated the possibility of performing tests of GR on binary black hole (BBH) events, employing mainly two different waveform models, IMRPhenomPv2 (phenomenological waveform model for a precessing BBH system) [43][44][45][58,59,60] and SEOBNRv4_ROM (reduced-order effective one body (EOB, waveform model for a non-precessing binary system) [46][61].
There is a significant increase in the detection rate as the detectors improve their sensitivities through first, second, and third observing runs of LIGO-Virgo detectors. Interestingly, it is possible to infer information from multiple events by combining the data from each event. The combined bounds help to improve our understanding of binary population properties in general. As we combine results, the statistical uncertainty that arises due to instrumental noise lessens. Notice that this instrumental noise does not include the uncertainty contributions from the systematic errors of gravitational waveform modeling [47][48][49][50][51][52][53][62,63,64,65,66,67,68], calibration of the detectors, and power spectral density (PSD) estimation uncertainties [54][55][56][57][58][69,70,71,72,73]. Sometimes, systematic errors can dominate the statistical errors and lead to false identification of GR violations, which we do not discuss here. Previous studies in References [9][53][59][9,68,74] discuss two different statistical approaches to estimate combined information on GR test parameters from multiple events. The first one (also called restricted or simple combining) assumes equal GR deviations across all the events independent of the physical parameters characterizing the binary, and this technique is well described and demonstrated for GWTC-1 events [59][74]. This assumption is generally incorrect as there are cases when the waveform model can arbitrarily deviate from GR depending upon the binary source properties. The second method, the hierarchical combining strategy, tries to overcome the issue of universality assumption by relaxing it. In this case, instead of assuming uniform GR deviation for all events, a Gaussian distribution models the non-GR parameter. The statistical properties (mean (μ) and standard deviation (σ)) of this distribution are obtained from the data itself, and the estimates are different for different models of gravity. We call the parameters μ and σ hyperparameters. If GR is the correct theory, the Gaussian distribution should center around zero. The astrophysical population properties of sources play a crucial role in estimating these statistical quantities [30].
