Computational Modeling of Reverse Total Shoulder Arthroplasty: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Conner Chen and Version 3 by Yichen Huang.

Reverse total shoulder arthroplasty (RTSA) is an established treatment for elderly patients with irreparable rotator cuff tears, complex proximal humerus fractures, and revision arthroplasty. Computational modeling has been used to investigate the effects of implant design, intraoperative component placement, and surgical technique on postoperative shoulder biomechanics after RTSA, with the findings ultimately used to elucidate and mitigate complications.

  • reverse shoulder prosthesis
  • finite element model
  • biomechanical model
  • rigid body model

1. Introduction

Reverse total shoulder arthroplasty (RTSA) has traditionally been used in the treatment of patients with a rotator cuff-deficient arthritic shoulder. However, over recent years, indications for RTSA have expanded to include irreparable rotator cuff tears, complex proximal humerus fractures in elderly patients, severe glenoid bone loss, revision arthroplasty, and tumour resection. In the United States, the number of primary RTSAs has almost tripled from 2012 to 2017, accounting for around 60% of all total shoulder arthroplasty procedures in 2017 [1]. In Australia, over 80% of total shoulder arthroplasty procedures performed in 2019 were RTSA [2].
RTSA, originally designed by Professor Paul Grammont in 1985, reverses the ball-and-socket anatomy of the anatomical glenohumeral joint [3]. This has the effect of medialising the centre of rotation of the glenohumeral joint, thereby increasing the moment arms (leverage) of the deltoid and facilitating the recruitment of more of its fibres during elevation [4][5][6]. The semi-constrained joint articulation confers stability, compensating for absence of rotator cuff muscles to a degree, while the prosthesis design also distalizes the humerus which tensions the deltoid, ultimately allowing for increased force generation and range of joint motion [7].
Despite the biomechanical benefits and widespread use of RTSA, complication rates remain a concern [8][9][10][11][12][13][14][15][16]. A recent study of 4124 shoulders with RTSA reported a complication rate of 16.1% [17]. Shoulder instability, periprosthetic fracture, infection, and component loosening are the leading causes of revision RTSA [17][18]. Scapular notching, acromial fractures, instability, and component loosening are a consequence of post-operative joint biomechanics and can be directly attributed to implant design and placement. The need for a deeper understanding of muscle and joint function after RTSA, to inform strategies to mitigate complication, has motivated the development of more sophisticated computational models of RTSA. 

2. Computational Modeling Techniques

Computational modeling of RTSA facilitates estimation of muscle and joint loading, which is currently impossible to measure non-invasively in vivo. Modeling and simulation of RTSA has played a critical role in guiding implant positioning and surgical technique [19][20][21][22], prosthesis selection [23][24], implant design [25][26], and post-operative rehabilitation prescription [27][28]. To date, most modeling and simulation tools require high levels of expertise and are generally restricted to the research setting.
Biomechanical computer models are broadly categorized into three groups: rigid body models, finite element (FE) models, and multi-body models. Rigid body models characterize bones as non-deformable segments. Through simulating joint kinematics and internal and external forces, these models are used to investigate changes in muscle and joint function after RTSA [29][30]. The primary advantage of rigid body models is that they can run quickly and at a low computational cost. For example, shoulder muscle forces during upper limb elevation can be calculated in several minutes using a subject-specific rigid body model (Figure 1A) [28][31]; however, since deformation mechanics is neglected, the internal stresses and strains in the bone and implant cannot be accurately evaluated using this method. An important utility of rigid body models has been in their capacity to estimate the influence of arthroplasty on muscle moment arms, muscle and joint forces, and range of motion (ROM) at the shoulder, which are primary indicators of implant functional performance [21][23][24][29][30][31][32][33][34][35][36][37][38][39][40].
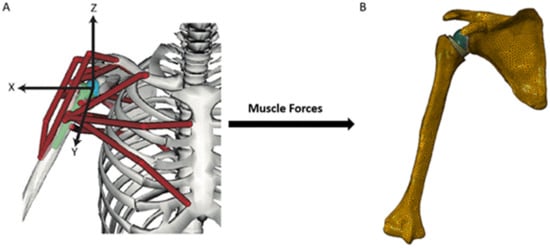
Jcm 10 05336 g001 550
Figure 1. A multi-body modeling framework used to investigate joint stability after RTSA [28], including a rigid body model to simulate muscle and joint loading at the shoulder (A), and a FE model to calculate internal stresses and strains at the bone and implant (B). The muscle and joint forces calculated from the rigid body model were input into the finite element model and used to drive simulations of joint loading during activities of daily living.
In contrast, FE models provide estimates of material deformation by discretization of structures into a finite number of elements, each element of which can be interrogated for load response such as stress, strain and displacement. This may reveal, for instance, how joint load is transmitted to bone via joint contact loading. The FE method has been used to investigate wear, component fixation, and joint stability after RTSA [41][42][43][44][45], which has aided in implant selection, intraoperative positioning, and fixation [20][44][46][47]. However, in contrast to rigid body models, FE model simulations can be computationally expensive. A FE model of the shoulder after RTSA, containing around half a million elements (Figure 1B), takes more than thirty minutes to run using a standard desktop computer [28].
Finally, multi-body musculoskeletal models input muscle and/or joint reaction force estimations from a secondary model simulation, typically derived from a rigid body model, into a FE analysis. This approach provides a basis for muscle and joint force prediction, as well as bone and implant deformation. Multi-body modeling has been used to assess the performances of different implant designs and surgical techniques in RTSA, with the capability to take into account accurate and physiologically meaningful boundary conditions [28][48][49][50][51].

References

  1. Best, M.J.; Aziz, K.T.; Wilckens, J.H.; McFarland, E.G.; Srikumaran, U. Increasing incidence of primary reverse and anatomic total shoulder arthroplasty in the United States. J. Shoulder Elb. Surg. 2021, 30, 1159–1166.
  2. Australian Orthopaedic Association; National Joint Replacement Registry. Hip, Knee & Shoulder Arthroplasty: 2020 Annual Report; AOA: Adelaide, Australia, 2020; pp. 1–474.
  3. Grammont, P.; Trouilloud, P.; Laffay, J.P.; Deries, X. Etude et réalisation d’une nouvelle prothèse d’épaule. Rhumatologie 1987, 39, 407–418.
  4. Ackland, D.C.; Roshan-Zamir, S.; Richardson, M.; Pandy, M.G. Moment arms of the shoulder musculature after reverse total shoulder arthroplasty. J. Bone Jt. Surg. -Am. Vol. 2010, 92, 1221–1230.
  5. Ackland, D.C.; Richardson, M.; Pandy, M.G. Axial rotation moment arms of the shoulder musculature after reverse total shoulder arthroplasty. J. Bone Jt. Surg. -Am. Vol. 2012, 94, 1886–1895. Ackland, D.; Richardson, M.; Pandy, M.G. Axial rotation moment arms of the shoulder musculature after reverse total shoulder arthroplasty. J. Bone Jt. Surg. -Am. Vol. 2012, 94, 1886–1895.
  6. Ackland, D.C.; Patel, M.; Knox, D. Prosthesis design and placement in reverse total shoulder arthroplasty. J. Orthop. Surg. Res. 2015, 10, 101.
  7. Gerber, C.; Pennington, S.D.; Nyffeler, R.W. Reverse total shoulder arthroplasty. J. Am. Acad. Orthop. Surg. 2009, 17, 284–295.
  8. Boileau, P.; Watkinson, D.; Hatzidakis, A.M.; Hovorka, I. Neer award 2005: The grammont reverse shoulder prosthesis: Results in cuff tear arthritis, fracture sequelae, and revision arthroplasty. J. Shoulder Elb. Surg. 2006, 15, 527–540.
  9. Ernstbrunner, L.; Andronic, O.; Grubhofer, F.; Camenzind, R.S.; Wieser, K.; Gerber, C. Long-term results of reverse total shoulder arthroplasty for rotator cuff dysfunction: A systematic review of longitudinal outcomes. J. Shoulder Elb. Surg. 2019, 28, 774–781.
  10. Ernstbrunner, L.; Rahm, S.; Suter, A.; Imam, M.A.; Catanzaro, S.; Grubhofer, F.; Gerber, C. Salvage reverse total shoulder arthroplasty for failed operative treatment of proximal humeral fractures in patients younger than 60 years: Long-term results. J. Shoulder Elb. Surg. 2020, 29, 561–570.
  11. Ernstbrunner, L.; Suter, A.; Catanzaro, S.; Rahm, S.; Gerber, C. Reverse total shoulder arthroplasty for massive, irreparable rotator cuff tears before the age of 60 years: Long-term results. J. Bone Jt. Surg. Am. 2017, 99, 1721–1729.
  12. Ernstbrunner, L.; Werthel, J.D.; Wagner, E.; Hatta, T.; Sperling, J.W.; Cofield, R.H. Glenoid bone grafting in primary reverse total shoulder arthroplasty. J. Shoulder Elb. Surg. 2017, 26, 1441–1447.
  13. Gerber, C.; Canonica, S.; Catanzaro, S.; Ernstbrunner, L. Longitudinal observational study of reverse total shoulder arthroplasty for irreparable rotator cuff dysfunction: Results after 15 years. J. Shoulder Elb. Surg. 2018, 27, 831–838.
  14. Werner, C.M.L.; Steinmann, P.A.; Gilbart, M.; Gerber, C. Treatment of painful pseudoparesis due to irreparable rotator cuff dysfunction with the delta III reverse-ball-and-socket total shoulder prosthesis. J. Bone Jt. Surg. -Am. Vol. 2005, 87, 1476–1486.
  15. Nabergoj, M.D.P.; Collin, P.; Trebše, R.; Lädermann, A. Mechanical complications and fractures after Reverse shoulder arthroplasty related to different design types and their rates. Part I. EFORT Open Rev. in press.
  16. Nabergoj, M.D.P.; Collin, P.; Trebše, R.; Lädermann, A. Radiological changes, infections and neurological complications after Reverse shoulder arthroplasty related to different design types and their rates. Part II. EFORT Open Rev. in press.
  17. Bohsali, K.; Bois, A.; Wirth, M. Complications of shoulder arthroplasty. J. Bone Jt. Surg. -Am. Vol. 2017, 99, 256–269.
  18. Markes, A.R.; Cheung, E.; Ma, C.B. Failed reverse shoulder arthroplasty and recommendations for revision. Curr. Rev. Musculoskelet. Med. 2020, 13, 1–10.
  19. Ingrassia, T.; Nigrelli, V.; Ricotta, V.; Nalbone, L.; D’Arienzo, A.; D’Arienzo, M.; Porcellini, G. A new method to evaluate the influence of the glenosphere positioning on stability and range of motion of a reverse shoulder prosthesis. Injury 2019, 50 (Suppl. 2), S12–S17.
  20. Zhang, M.; Junaid, S.; Gregory, T.; Hansen, U.; Cheng, C.K. Effect of baseplate positioning on fixation of reverse total shoulder arthroplasty. Clin. Biomech. 2019, 62, 15–22.
  21. Ackland, D.C.; Wu, W.; Thomas, R.; Patel, M.; Page, R.; Sangeux, M.; Richardson, M. Muscle and joint function after anatomic and reverse total shoulder arthroplasty using a modular shoulder prosthesis. J. Orthop. Res. 2019, 37, 1988–2003.
  22. Kim, S.J.; Jang, S.W.; Jung, K.H.; Kim, Y.S.; Lee, S.J.; Yoo, Y.S. Analysis of impingement-free range of motion of the glenohumeral joint after reverse total shoulder arthroplasty using three different implant models. J. Orthop. Sci. 2019, 24, 87–94.
  23. Eno, J.T.; Kontaxis, A.; Novoa-Boldo, A.; Windsor, E.; Chen, X.; Erickson, B.J.; Warren, R.F.; Dines, D.M.; Dines, J.S.; Gulotta, L.V.; et al. The biomechanics of subscapularis repair in reverse shoulder arthroplasty: The effect of lateralization and insertion site. J. Orthop. Res. 2020, 38, 888–894.
  24. King, J.J.; Greene, A.T.; Hamilton, M.A.; Diep, P.T.; Gil, J.; Wright, T.W.; Schoch, B.S. The over-the-top subscapularis repair in reverse shoulder arthroplasty: Biomechanical evaluation of a novel technique. JSES Open Access 2019, 3, 304–310.
  25. James, J.; Huffman, K.R.; Werner, F.W.; Sutton, L.G.; Nanavati, V.N. Does glenoid baseplate geometry affect its fixation in reverse shoulder arthroplasty? J. Shoulder Elb. Surg. 2012, 21, 917–924.
  26. Ladermann, A.; Denard, P.J.; Boileau, P.; Farron, A.; Deransart, P.; Terrier, A.; Ston, J.; Walch, G. Effect of humeral stem design on humeral position and range of motion in reverse shoulder arthroplasty. Int. Orthop. 2015, 39, 2205–2213.
  27. Terrier, A.; Reist, A.; Merlini, F.; Farron, A. Simulated joint and muscle forces in reversed and anatomic shoulder prostheses. J. Bone Jt. Surg. Br. Vol. 2008, 90, 751–756.
  28. Ackland, D.C.; Robinson, D.L.; Wilkosz, A.; Wu, W.; Richardson, M.; Lee, P.; Tse, K.M. The influence of rotator cuff tears on muscle and joint-contact loading after reverse total shoulder arthroplasty. J. Orthop. Res. 2019, 37, 211–219.
  29. Glenday, J.; Kontaxis, A.; Roche, S.; Sivarasu, S. Effect of humeral tray placement on impingement-free range of motion and muscle moment arms in reverse shoulder arthroplasty. Clin. Biomech. 2019, 62, 136–143.
  30. Hamilton, M.A.; Diep, P.; Roche, C.; Flurin, P.H.; Wright, T.W.; Zuckerman, J.D.; Routman, H. Effect of reverse shoulder design philosophy on muscle moment arms. J. Orthop. Res. 2015, 33, 605–613.
  31. Wu, W.; Lee, P.V.S.; Bryant, A.L.; Galea, M.; Ackland, D.C. Subject-specific musculoskeletal modeling in the evaluation of shoulder muscle and joint function. J. Biomech. 2016, 49, 3626–3634.
  32. Berhouet, J.; Kontaxis, A.; Gulotta, L.V.; Craig, E.; Warren, R.; Dines, J.; Dines, D. Effects of the humeral tray component positioning for onlay reverse shoulder arthroplasty design: A biomechanical analysis. J. Shoulder Elb. Surg. 2015, 24, 569–577.
  33. Berton, A.; Gulotta, L.V.; Petrillo, S.; Florio, P.; Longo, U.G.; Denaro, V.; Kontaxis, A. The effect of humeral version on teres minor muscle moment arm, length, and impingement in reverse shoulder arthroplasty during activities of daily living. J. Shoulder Elb. Surg. 2015, 24, 578–586.
  34. Costantini, O.; Choi, D.S.; Kontaxis, A.; Gulotta, L.V. The effects of progressive lateralization of the joint center of rotation of reverse total shoulder implants. J. Shoulder Elb. Surg. 2015, 24, 1120–1128.
  35. Quental, C.; Folgado, J.; Ambrosio, J.; Monteiro, J. Multibody system of the upper limb including a reverse shoulder prosthesis. J. Biomech. Eng. 2013, 135, 111005.
  36. Martins, A.; Quental, C.; Folgado, J.; Ambrosio, J.; Monteiro, J.; Sarmento, M. Computational reverse shoulder prosthesis model: Experimental data and verification. J. Biomech. 2015, 48, 3242–3251.
  37. Hoenecke, H.R., Jr.; Flores-Hernandez, C.; D′Lima, D.D. Reverse total shoulder arthroplasty component center of rotation affects muscle function. J. Shoulder Elb. Surg. 2014, 23, 1128–1135.
  38. Walker, D.R.; Kinney, A.L.; Wright, T.W.; Banks, S.A. How sensitive is the deltoid moment arm to humeral offset changes with reverse total shoulder arthroplasty? J. Shoulder Elb. Surg. 2016, 25, 998–1004.
  39. Nikooyan, A.A.; Veeger, H.E.; Westerhoff, P.; Bolsterlee, B.; Graichen, F.; Bergmann, G.; van der Helm, F.C. An EMG-driven musculoskeletal model of the shoulder. Hum. Mov. Sci. 2012, 31, 429–447.
  40. Liou, W.; Yang, Y.; Petersen-Fitts, G.R.; Lombardo, D.J.; Stine, S.; Sabesan, V.J. Effect of lateralized design on muscle and joint reaction forces for reverse shoulder arthroplasty. J. Shoulder Elb. Surg. 2017, 26, 564–572.
  41. Nalbone, L.; Adelfio, R.; D′Arienzo, M.; Ingrassia, T.; Nigrelli, V.; Zabbara, F.; Paladini, P.; Campi, F.; Pellegrini, A.; Porcellini, G. Optimal positioning of the humeral component in the reverse shoulder prosthesis. Musculoskelet. Surg. 2014, 98, 135–142.
  42. Ribeiro, N.S.; Folgado, J.; Fernandes, P.R.; Monteiro, J. Wear analysis in anatomical and reversed shoulder prostheses. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 883–892.
  43. Permeswaran, V.N.; Caceres, A.; Goetz, J.E.; Anderson, D.D.; Hettrich, C.M. The effect of glenoid component version and humeral polyethylene liner rotation on subluxation and impingement in reverse shoulder arthroplasty. J. Shoulder Elb. Surg. 2017, 26, 1718–1725.
  44. Chae, S.W.; Lee, H.; Kim, S.M.; Lee, J.; Han, S.H.; Kim, S.Y. Primary stability of inferior tilt fixation of the glenoid component in reverse total shoulder arthroplasty: A finite element study. J. Orthop. Res. 2016, 34, 1061–1068.
  45. Terrier, A.; Merlini, F.; Pioletti, D.P.; Farron, A. Comparison of polyethylene wear in anatomical and reversed shoulder prostheses. J. Bone Jt. Surg. Br. Vol. 2009, 91, 977–982.
  46. Langohr, G.D.; Willing, R.; Medley, J.B.; Athwal, G.S.; Johnson, J.A. Contact mechanics of reverse total shoulder arthroplasty during abduction: The effect of neck-shaft angle, humeral cup depth, and glenosphere diameter. J. Shoulder Elb. Surg. 2016, 25, 589–597.
  47. Bonnevialle, N.; Geais, L.; Muller, J.H.; Shoulder Friends Institute; Berhouet, J. Effect of RSA glenoid baseplate central fixation on micromotion and bone stress. JSES Int. 2020, 4, 979–986.
  48. Zeng, W.; Lewicki, K.A.; Chen, Z.; Van Citters, D.W. The evaluation of reverse shoulder lateralization on deltoid forces and scapular fracture risk: A computational study. Med. Nov. Technol. Devices 2021, 11, 100076.
  49. Lockhart, J.S.; Wong, M.T.; Langohr, G.D.G.; Athwal, G.S.; Johnson, J.A. The effect of load and plane of elevation on acromial stress after reverse shoulder arthroplasty. Shoulder Elb. 2021, 13, 388–395.
  50. Wong, M.T.; Langohr, G.D.G.; Athwal, G.S.; Johnson, J.A. Implant positioning in reverse shoulder arthroplasty has an impact on acromial stresses. J. Shoulder Elb. Surg. 2016, 25, 1889–1895.
  51. Sabesan, V.J.; Lima, D.J.L.; Rudraraju, R.T.; Yang, Y.; Stankard, M.; Sheth, B.K.; Liou, W.W. Does acromion anatomy affect the risk of acromion stress fracture after reverse shoulder arthroplasty? Semin. Arthroplast. JSES 2021, 31, 8–14.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback