The mine ventilation system is an indispensable component to improve coal mining efficiency and ensure the safety production. Only by clearly grasping the comprehensive evaluation quality of ventilation system can effective countermeasures be formulated. This paper establishes an evaluation index system for mine ventilation system by combining qualitative survey with quantitative research. Specifically, the primary indicators are screened through R-type clustering and coefficient of variation method. The weight of each index is determined by the entropy weight method. Moreover, the TOPSIS method are used to evaluate the quality of the mine ventilation system. Finally, this evaluation system is used to evaluate the ventilation renovation project in the production mining area of the Sihe mine. The evaluation results verify the effectiveness of the establishment of mine ventilation evaluation index system and evaluation methods.
- effectiveness evaluation
- R clustering
- coefficient of variation
- optimization
1. Introduction
2. Construction of Evaluation Index System for Mine Ventilation System
2.1. Weight Calculation Based on the Entropy Method


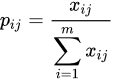

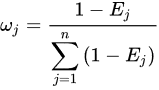
3. Evaluation Model of TOPSIS






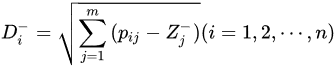
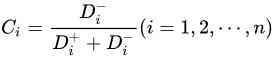
4. Conclusions
-
The 20 evaluation indexes of mine ventilation were selected through expert consultation and reference summary. Then the primary index was screened through R-clustering and the coefficient of variation method. The results showed that 80% of the indicators after screening could reflect 84.05% of the original information. Apparently, this method is improved by approximately 4% compared with Gao [26].
- Aiming at the properties of enormous sample data, a complex indicator system and the possibility of future ventilation evaluation system expansion, the TOPSIS method was utilized to evaluate the mine ventilation evaluation system. The ventilation evaluation system was applied to the Sihe mine. The ventilation simulation results showed that Scheme 4; Scheme 6 had lower negative pressure and higher air volume compared to other schemes. Compared with Scheme 4, Scheme 6 was more time-saving and labor-saving in the renovation project. Compared with Scheme 5, Scheme 6 had great advantages in terms of system power consumption, effective air volume rate, and equivalent orifice. The actual test results were essentially consistent with the simulation results of Scheme 6. The correctness of the optimized scheme is verified by simulation results and practical renovation.
References
- Lechner, A.M.; Kassulke, O.; Unger, C. Spatial assessment of open cut coal mining progressive rehabilitation to support the monitoring of rehabilitation liabilities. Resour. Policy 2016, 50, 234–243.
- Gao, Y.; Liu, D.; Zhang, X.; He, M. Analysis and Optimization of Entry Stability in Underground Longwall Mining. Sustainability 2017, 9, 2079.
- Zhang, X.H.; Wang, L.G.; Feng, X.L. Fuzzy integrated evaluation for safety of metal mine ventilation system. China Min. Mag. 2010, 19, 93–96.
- Lee, D.-K. Optimal design of mine ventilation system using a ventilation improvement index. J. Min. Sci. 2016, 52, 762–777.
- Bai, Y.Y.; Wen, C.P.; Chen, Z.H. Evaluation of mine ventilation system working condition based on catastrophe progression method. Electron. J. Geotech. Eng. 2016, 21, 7517–7525.
- Ren, S.; Wang, X.S.; Jiang, D.Y. Multiple fuzzy integrated evaluation for safety of mine ventilating system. China Saf. Sci. J. 2009, 19, 127–131.
- Li, X.F.; Wu, Y.; Zhao, Z.Y.; Liu, Y.; Xie, P.; Zou, J.; Xuan, P.; Zhu, J.; Huang, L. Research on index system and comprehensive evaluation method of China’s electricity spot market. In Proceedings of the 8th Renewable Power Generation Conference, Shanghai, China, 24–25 October 2019; pp. 1–7.
- Jing, G.X.; Yao, R.; Zhang, F.R. Grey comprehensive judgement for the reliability of mining ventilation system. China Saf. Sci. J. 2001, 11, 65–68.
- Shi, X.Z.; Zhou, J. Reliability assessment for mine ventilation system safety using Fisher discriminant analysis. J. Min. Saf. Eng. 2010, 27, 562–567.
- Su, Y.Y.; Liu, X.H.; Li, J.Z. Mine ventilation system index system reduction and its safety evaluation. China Saf. Sci. J. 2013, 23, 83–89.
- Liu, H.T.; Li, L.L. Comprehensive Evaluation Analysis of Mine Gas Safety Based on Integrated Method. In Proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009; IEEE: Washington, DC, USA, 2009; pp. 1–4.
- Xiao, P.; Ding, Y.; Li, S.G. Evaluation of Gas Prevention and Control System Based on Unascertained Measurement Mode. China Saf. Sci. J. 2017, 27, 98–103.
- Zhu, W. A comprehensive benefit evaluation model of multi energy complementary system operation for different applica-tion scenarios. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference, Washington, DC, USA, 16–18 February 2021; 2021; pp. 1–5.
- Yi, D.F.; Liu, D. Construction of the Coal Mine Production Safety Management Evaluation System Based on the Sustainable Development. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–5.
- Li, Y.M.; Chen, Z. Evaluation Index System and Evaluation Method of China’s Regional Potential for Electrical Energy Sub-stitution. Math. Probl. Eng. 2018, 2018, 3834921.
- Zhang, K.; Zhu, R.; Song, R.; Shi, F.; Shi, S.; Fang, C. A Mesh Analysis Model and the Coherent Evaluation Index System for Urban Distribution Network Planning. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 443–447.
- Guo, S.; Feng, P.; Hu, W.; Xu, C.; Xiao, J.; Xu, J. Multi-index Comprehensive Evaluation for the River Source Heat Pump Energy Supply System Based on Dynamic Weighting. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; IEEE: Washington, DC, USA, 2021; pp. 1177–1184.
- Zhao, T.; Wang, S.; Zuo, J.; Duan, X.; Wang, X. Performance Evaluation of Smart Meters Based on Grey Relational Analysis. In Proceedings of the 2018 10th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China,, 25–26 August 2018; IEEE: Washington, DC, USA, 2018; Volume 2, pp. 312–315.
- Zhang, Z.; Lu, H. Research on Power Spot Market Comprehensive Index System and Evaluation Method. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; IEEE: Washington, DC, USA, 2020; pp. 3479–3484.
- Shi, H. A Method Used for Quality Assessment of Construction Project Based on FCE and Group-decision AHP. In Proceedings of the 2009 Second International Symposium on Electronic Commerce and Security, Nanchang, China, 22–24 May 2009; IEEE: Washington, DC, USA, 2009; pp. 333–336.
- Jia, N.P.; You, Y.Q.; Lu, Y.J.; Guo, Y.; Yang, K.W. Research on the Search and Rescue System-of-Systems Capability Evalua-tion Index System Construction Method Based on Weighted Supernetwork; IEEE Access: Washington, DC, USA, 2019; Volume 7, pp. 97401–97425.
- Jiang, F.; Guo, J.T.; Li, X.Y.; Chen, G.; Yang, W.C.; Wang, X.L.; Zhang, S.; Li, M. Evaluation of a Lead-Zinc Mine’s Ventilation System Based on Unascertained Measurement Model. In Proceedings of the 11th International Symposium on Computational Intelligence and Design, Hangzhou, China, 8–9 December 2018; pp. 208–211.
- Cheng, J.; Luo, Y. Mathematical models for optimizing and evaluating mine ventilation systems. In Proceedings of the 13th United States/North American Mine Ventilation Symposium, Sudbury, ON, Canada, 13–16 June 2010; pp. 387–393.
- Zhou, Z.-Y.; Kizil, M.; Chen, Z.-W.; Chen, J.-H. A new approach for selecting best development face ventilation mode based on G1-coefficient of variation method. J. Cent. South Univ. 2018, 25, 2462–2471.
- Yan, F.; Li, Z.-J.; Dong, L.-J.; Huang, R.; Cao, R.-H.; Ge, J.; Xu, K.-L. Cloud model-clustering analysis based evaluation for ventilation system of underground metal mine in alpine region. J. Cent. South Univ. 2021, 28, 796–815.
- Gao, J.J. Establishments and Applications of Evaluation Index System for Complex Ventilation Network Optimization. Ph.D. Thesis, Liaoning Technical University, Fuxin, China, 2017.
- Liu, Y.; Liu, J.; Shao, G.; Yu, J. Research on Construction of Evaluation Index System of R&D Platform. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2021; IEEE: Washington, DC, USA, 2021; pp. 891–894.
