Magnetic Guiding | Encyclopedia MDPI

Magnetic Guiding: Comparison

Please note this is a comparison between Version 2 by Peter Blümler and Version 1 by Peter Blümler.

Magnetic guidance is understood as a remote, untethered and contact-free control of the movements of an object via magnetic interactions. The movements should happen on arbitrary trajectories inside a container caused by an external device.

In this review the idea of remote magnetic guiding is developed from the underlying physics of a concept that allows for bijective force generation over the inner volume of magnet systems. This concept can equally be implemented by electro- or permanent magnets.

steering
magnetic force
magnetic drug targeting (MDT)
nanoparticle
SPIO
ferrofluid
superparamagnetic
ferromagnetic
Halbach magnets
dipole
quadrupole
cells
micro-robots
endoscopic capsules
magnetic resonance imaging
MRI

Examples:

Typical examples of such magnetically guided objects are endoscopic capsules for inspection of the gastrointestinal tract or superparamagnetic nanoparticles suggested for local therapy, which therefore have to be moved through blood vessels.

reviews:

magnetically guided medical devices ^[1]^[2]^[3]
miniature robots^[4]
nanoparticles in microfluidics and nanomechanics^[5] for drug delivery^[6]^[7]^[8]
hyperthermia, and alternative local magnetic therapeutic effects^[9]^[10]
tissue engineering^[11]^[12]^[13]
as well as magnet systems for this purpose^[14]
monograph^[15] treating most of these topics

CHistory/Pronceptblem:

Magnetic guiding has been an established technique since 1897^[16], when Ferdinand Braun invented magnetic guidance of charged particles (electrons or ions) by cathode ray tubes where the electrons are emitted from a cathode into an evacuated tube, accelerated by an anode, and deflected by magnetic fields (used en masse in analogue oscilloscopes and television screens). The magnetic deflection is based on the Lorentz force F_L=qv \vec{F}_L = q \vec{v} \times \vec{B} × B

{\overset{⇀}{F}}_{L} = q \overset{⇀}{v} \times \overset{⇀}{B},

which is perpendicular to the direction of the magnetic flux density B \vec{B} and the flight direction of the particles with charge q q and velocity \vec{v} v. However, the situation is very different if an electrically neutral paramagnetic material is exposed to magnetic fields. The force is then the gradient (\vec{\nabla} = [\partial/\partial x,\partial/\partial y,\partial/\partial z]) (∇ = [∂/∂x, ∂/∂y, ∂/∂z]) of the magnetic field acting on the object with a magnetic moment \vec{m} m,

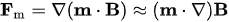So what happens to a small paramagnetic object in an inhomogeneous magnetic field? It is hard to imagine that an object that should be guided through space is not freely movable (at least in two dimensions). If the object has an intrinsic fixed direction of m (e.g., remanent magnetization), it is rotated by the magnetic torque,

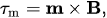
\vec{F}_m = \vec{\nabla} (\vec{m} \cdot \vec{B}) \approx (\vec{m} \cdot \vec{\nabla}) \vec{B}

(1)

The right simplified term is usually correct for the applications discussed here, however, it is not generally the case. Particularly, it assumes that m is not dependent on B, which depends on the material and the range of B .

So what happens to a small paramagnetic object in an inhomogeneous magnetic field? It is hard to imagine that an object that should be guided through space is not freely movable (at least in two dimensions). If the object has an intrinsic fixed direction of \vec{m} (e.g., remanent magnetization), it is rotated by the magnetic torque

\vec{\tau}_m = \vec{m} \times \vec{B},

(2)

until the crosstil the cross-product becomes zero or \vec{m} m is parallel to \vec{B} B. If the object has initially (at B=0 B = 0 ) no preferred direction of \vec{m} m, the actual field will magnetize it (orient the electron spins) along \vec{B} B. Either way, as a result, \vec{m} m points along \vec{B} B, which is very unfortunate with respect to guiding, because the dot-product in EquationF_m = (1m · ∇) B will lose its sign for two parallel vectors and the material will always move towards higher magnetic fields (cf. Figure 1a,b). . This is an everyday observation, as e.g., paper clips are attracted equally by the north and south pole of a permanent magnet. For steering this is like using a clipper without a sail. Almost independently of what one tries with the rudder, the boat will go to where the winds or currents move it. In electrodynamics, this is also known as Earnshaw’s theorem^[17], and it is the reason why permanent magnets were originally not considered as being useful for magnetic guidance, because as their name suggests they are permanent and cannot be switched on or off.

Figure 1. Illustration of the suggested guiding principle. A small magnetizable sphere serves as the object to be guided by a large deflecting bar magnet. The colors indicate the magnitude of the local magnetic flux density (see color bars on the left, B_{max} B_max in (a,b) is roughly a quarter of that in (c,d)). The black lines are field lines. A zoom of the region around the object is shown on the inserts. The top rows (a,b) just show the field generated by the deflection magnet, while in (c,d) a strong and homogeneous field is superimposed to the scenario above. The difference between the columns is the orientation (south- and north-pole) of the deflection magnet. (a,b) Changing the magnet’s orientation has no effect on the movement of the object (white arrow), because the object is magnetized in opposite directions as well and just moves to the highest flux density. The additional homogeneous field in (c,d) essentially keeps the magnetization direction of the object along its horizontal direction. The field of the deflecting magnet now causes the opposite magnetic “landscape” around the object and hence moves in opposite directions. The data were generated using FEMM but should serve for illustration purposes only.

Solution:

Now the question arises why guiding charged particles is so straightforward, while it is so difficult to control the collective spin of electrons in materials magnetically? The reason is the bijective direction ( \vec{v} ) of the electron beam, which is just slightly deflected by steering fields. This suggests that a preferred direction would also be beneficial for steering paramagnetic objects. This is tantamount to a magnetic field that just orients (polarizes) the particles without exerting a force on them. For static magnetic fields, this request can be fulfilled by applying a strong but homogeneous magnetic flux density, B_{hom} , which magnetizes the object along its direction. An additional, small, and spatially-dependent steering or deflecting field can then act as a perturbation but with full directional control (cf.

Now the question arises why guiding charged particles is so straightforward, while it is so difficult to control the collective spin of electrons in materials magnetically? The reason is the bijective direction (v) of the electron beam, which is just slightly deflected by steering fields. This suggests that a preferred direction would also be beneficial for steering paramagnetic objects. This is tantamount to a magnetic field that just orients (polarizes) the particles without exerting a force on them. For static magnetic fields, this request can be fulfilled by applying a strong but homogeneous magnetic flux density, B_hom, which magnetizes the object along its direction. An additional, small, and spatially-dependent steering or deflecting field can then act as a perturbation but with full directional control (cf.

Figure 1c,d). Ideally, this deflecting field will have a linear spatial dependence, i.e., a constant gradient (The fact that \overline{\overline{G}} is a tensor is ignored for the moment), \vec{\nabla}\vec{B}=G , and the total field in such an experiment is then

c,d). Ideally, this deflecting field will have a linear spatial dependence, i.e., a constant gradient (The fact that G is a tensor is ignored for the moment), ∇ B = G , and the total field in such an experiment is then

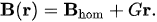
\vec{B}(\vec{r})=\vec{B}_{hom}+G\vec{r}.

(3)

With the reasonable assumption that there is no strong spatial variation of the magnetic moment over the sample, one could conclude that F_m=mG F_m = mG (because

\overset{⇀}{\nabla} {\overset{⇀}{B}}_{hom} = 0

∇B_hom = 0 $\overset{⇀}{\nabla} {\overset{⇀}{B}}_{hom} = 0$

). Under certain limits this is correct, but unfortunately magnetism is not quite that simple. Things become a bit more complicated due to Maxwell’s (or Gauss’) law

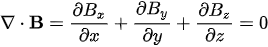
\vec{\nabla}\cdot\vec{B}=\frac{\partial B_x}{\partial x}+\frac{\partial B_y}{\partial y}+\frac{\partial B_z}{\partial z} = 0 .(4) Hence, there cannot be a single gradient field at any point. Either the field has to be homogeneous or the sum of all its spatial derivatives have to cancel. For the simple case of a perfect quadrupolar field , this could be for instance ∂Bx /∂x = +G  \partial B_x/\partial x = +G and \partial B_y/\partial y = -G ∂By /∂y = -G consequently Ethe last equation (4) then dictates ∂Bz /∂z \partial B_z/\partial z = 0 = 0. Then a more detailed representation of EqB(r) will be

The deflecting field is written here in the most general form as a gradient tensor (G). As discussed ation (3)bove, the magnetic moment of an object at r = [x, y, z]^Twill be

oriented parallel to B(r) (with unit vector e_B)

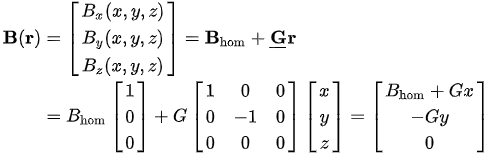
\begin{align*}\vec{B}(\vec{r}) &= \begin{bmatrix} B_x(x,y,z) \\B_y(x,y,z)\\B_z(x,y,z) \end{bmatrix} =\vec{B}_{hom} + G\vec{r} \\ &= B_{hom}\begin{bmatrix}1\\0\\0 \end{bmatrix}+G\begin{bmatrix}1&0&0\\0&-1&0\\0&0&0 \end{bmatrix} \begin{bmatrix}x\\y\\z \end{bmatrix} =\begin{bmatrix}B_{hom}+Gx\\-Gy\\0 \end{bmatrix} \end{align*} (5)

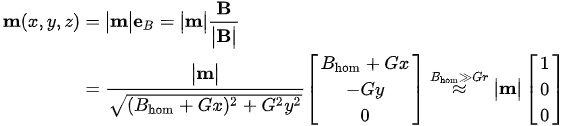
The deflecting field is written here in the most general form as a gradient tensor ( \overline{\overline{G}} ). As discussed above, the magnetic moment of an object at \vec{r}=[x,y,z]^T will be oriented parallel to \vec{B}(\vec{r}) (with unit vector \hat{e}_B )

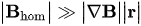
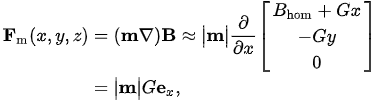
\begin{align*} \vec{m}(x,y,z) &= \big| \vec{m} \big| \hat{e}_B = \big| \vec{m} \big| \frac {\vec{B}} {\big|\vec{B}\big|} \\ &=\frac {\big| \vec{m} \big|} {\sqrt{(B_{hom}+Gx)^2+G^2y^2}} \begin{bmatrix}B_{hom}+Gx\\-Gy\\0 \end{bmatrix} \stackrel{B_{hom} \gg Gr}{\approx} \big| \vec{m}\big| \begin{bmatrix}1\\0\\0 \end{bmatrix} \end{align*} (6) The last approximation was already motivated in the discussion of Figure 1 and is the origin of bijection, namely that the homogeneous field must be much stronger than the local deflection field, so that its tensorial properties can be reduced to a vector via projection. The condition for this prerequisite is then[18] It is instructive to continue with this assumption to approximate the magnetic force

\big|\vec{B}_{hom}\big| \gg \big|\vec{\nabla}\vec{B} \big| \big|\vec{r} \big| (7)   Aor more fugenerall treatmy only the field component[18] of the deflection field, whillch is parallel to fBhom, determines the direction and ampllow but to clarify the concept, it iitude of the magnetic force. It is a very beneficial feature of this concept that there is no spatial dependence of the force vector in last equation, hence the guiding force is homogeneous or constant over that region where Bhom >> Gr is fulfinstructive to continlled . This is an important issue because other systems which guide an object by moving permanent magnets around the outside of the container (e.g.[19]) or use with the approximation from Equation (6). Then the magnetic force in Equation (1) simplifies t electromagnets on opposing ends of the container, also have to consider the non-linear drop of the magnetic field with distance (depending on their dimensions, the far-field of permanent magnets drops with an exponent between −2 and −3, and hence the force with −3 to −4). This can extremely complicate the control because the position of the object has to be known precisely to estimate speed and direction of motion. This is a problem that does not exist in the presented concept. Additionally, the movements are also not limited to the directio n of B.

\begin{align*} \vec{F}_m(x,y,z) & = ( \vec{m} \vec{\nabla})\vec{B} \approx \big| \vec{m} \big| \frac {\partial} {\partial x} \begin{bmatrix}B_{hom}+Gx\\-Gy\\0 \end{bmatrix} \\ & =\big| \vec{m} \big| G \hat{e}_x, \end{align*} (8)     or more generally only the field component of the deflection field, which is parallel to \vec{B}_{hom} , determines the direction and amplitude of the magnetic force. It is a very beneficial feature of this concept that there is no spatial dependence of the force vector in Equation (8), hence the guiding force is homogeneous or constant over that region where Equation (7) is fulfilled (cf. also Figure 5). This is an important issue because other systems which guide an object by moving permanent magnets around the outside of the container (e.g.[19]) or use electromagnets on opposing ends of the container, also have to consider the non-linear drop of the magnetic field with distance (depending on their dimensions, the far-field of permanent magnets drops with an exponent between −2 and −3, and hence the force with −3 to −4). This can extremely complicate the control because the position of the object has to be known precisely to estimate speed and direction of motion. This is a problem that does not exist in the presented concept. Additionally, the movements are also not limited to the direction of \vec{B} .

Examples:

CHistory/Pronceptblem:

Solution:

Further reading:

References