1. Introduction 

Imagine reducing the size of our fingers by one million times and being able to use them to probe the nanoworld. Now, it is easy to imagine that we could easily capture things of a similar size, such as dielectric nanoparticles, quantum dots with a DNA strand attached to them, proteins and viruses. More than that, we could have the ability to move them in space. In reality, although we cannot modify our fingers in this way, we have found a way to manipulate objects of that size using light!

For more than four centuries, it has been known that light can exert forces on objects ^[1]. Much later, in 1873, using Maxwell’s electromagnetic theory ^[2], the transfer of momentum from light to illuminated objects was described, resulting in the so-called radiation pressure that leads to objects moving along the direction of light propagation ^[3]. There were many experiments to follow that confirmed Poynting’s calculations, but all of them concluded with the fact that these optical forces were so small that it was difficult even to measure them, let alone utilise them in some meaningful application. In 1936, Beth experimentally demonstrated the transfer of angular momentum from light to a crystal plate and studied the change of polarisation of the beam due to the interaction with matter ^[4]. However, the birth of lasers in 1960 [5,6]^[5][6] was really what opened new possibilities and topics for research in the field of light-matter interactions.

As the use of lasers became more and more popular in science exploration, Arthur Ashkin, in 1970, experimentally demonstrated how optical radiation forces exerted by lasers can be used to change the motion of dielectric microparticles. He succeeded in trapping them by creating a stable optical potential well ^[7], thus establishing the new research topic that is known today as optical tweezers.

As always, nature follows its own rules, and soon the primary challenge for optical tweezers became apparent, i.e., the diffraction limit. It seemed to be impossible to focus light beyond the constraints imposed by this limit and, consequently, this created a restriction on the smallest size of particle that could be trapped. Subsequently, the next step in the field’s progress was to use surface plasmons excited on metallic nanostructures to confine light into highly intense optical fields, thus enabling superior trapping performance ^[8]. The first experimental demonstration of trapping using plasmonic structures was reported by Righini et al. ^[9] in 2007 and, since then, the field of plasmonic optical tweezers started developing rapidly and opened further scientific avenues for investigation.

2. Conventional Optical Tweezers

The Nobel Prize in Physics 2018 was awarded (50%) to Arthur Ashkin “for the optical tweezers and their application to biological systems”. The whole research field started when Ashkin calculated that “a power P=1 W of cw (continuous wave) argon laser light at λ=0.5145 μm focussed on a lossless dielectric sphere of radius r=λ and density =1 gm/cc gives a radiation pressure force \( F_{rad}=2qP/c=6.6×10^{−5} dyn \), where q, the fraction of light effectively reflected back, is assumed to be of order 0.1. The acceleration =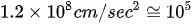times the acceleration of gravity” ^[7]. In SI units, this is equivalent to a radiation pressure force \( F_{rad}=0.66 nN \), leading to an acceleration of \( 1.2×10^6 m/s^2 \). In the same work, he demonstrated the first experimental approach to test his calculations on transparent, micron-sized latex spheres in liquids and gas and found that the radiation pressure exerted on the particles from a focussed laser beam was able to accelerate them along the direction of the beam. The measured velocities of the accelerated particles were in very good agreement with the theoretical predictions.

Ashkin next demonstrated trapping of particles using one laser beam and the wall of a glass cell, as well as using two counter-propagating beams with the same characteristics ^[7]. A few years later, Ashkin et al. [12]^[10], reported trapping of dielectric particles (10 μm–25 nm) using a single beam by focussing argon-laser light at 514.5 nm through a high numerical aperture objective lens (NA=1.25). This achievement is attributed to the existence of a force additional to that caused by the radiation pressure (from now on called the scattering force) which originates from the axial beam intensity gradient. It then becomes apparent that, whereas the scattering force depends on the optical intensity and has the direction of the incident beam, the gradient force depends on the intensity gradient and is directed along it from low to high intensities (for the case of particles with higher refractive index than the surrounding medium). Stable optical trapping can occur when these two forces are balanced.

The theoretical mechanism that explains this observation, depends on the relative size of the particle (radius, r) with respect to the wavelength of the laser light (λ). In both cases we assume spherical dielectric particles with refractive index higher than that of the surrounding environment.

For r≫λ, ray optics can be used and the reflection and transmission of the beam from the particle can give rise to the two forces:

Scattering force: \( F_{scat}=\sum_{i=1}^{N}\dfrac{n_m \cdot P_i}{c} \left[1+R_i \cos(2\theta_i)-\dfrac{T_i^2[\cos(2\theta_i-2 r_i)+R_i \cos(2\theta_i)]}{1+R_i^2+2R_i \cos(2 r_i)} \right] \)

Gradient force: \( F_{grad}=\sum_i^N \dfrac{n_m \cdot P_i}{c}\left[ R_i \sin(2 \theta_i) - \dfrac{T_i^2[\sin(2\theta_i - 2r_i)+R_i \sin(2 \theta_i)]}{1+R_i^2+2R_i \cos(2r_i)} \right] \),        

where the sum is over all N rays interacting with the particle, \( n_m \) is the refractive index of the particle, \( P_i \) is the power of the incident ray, \( c \) is the speed of light, \( R_i \) and \( T_i \) are Fresnel's reflection and transmission coefficients, \( \theta_i \) and \( r_i \) are the incidence and refraction angles of the rays measured from the normal to the surface of the particle.

For r≪λ, Rayleigh scattering is assumed and the particle is treated like a dipole in an external electromagnetic field \( (\vec{E}) \). The resulting time-averaged total force is:

\( \vec{F}=\frac{1}{4}\alpha'_d \nabla |\vec{E}|^2 + \frac{\sigma_{ext,d}}{c}\vec{S} + \frac{c\epsilon_0 \sigma_{ext,d}}{4 \omega i} \nabla \times (\vec{E} \times \vec{E}^*) \)

where \( \alpha'_d \) is the real part of the effective polarizability of the particle, \( \epsilon_0 \) the vacuum dielectric permittivity, \( \omega \) is the angular frequency, \( \sigma_{ext,d} \) is the extinction cross-section, i.e., the active area of the particle that causes part of the energy of the incident electromagnetic wave to be extinguished due to scattering and absorption from the particle. It, therefore, indicates the rate of energy loss from the incident wave. \( \vec{S} \) is the time-averaged real part of the Poynting vector of the incident wave.

It is easy to see that the force acting on a dipole consists of three terms; the third term is called the spin-curl force and is related to polarisation gradients in the electromagnetic field that arise when the polarisation is inhomogeneous. Using a defined polarisation of the incident beam, this term has a small value compared to the other two terms and that is why we usually neglect it in optical trapping experiments. The second term is the scattering force pointing in the direction of the Poynting vector, \( \vec{S} \), and arises from absorption and scattering phenomena that cause momentum transfer from the field to the particle. The first term is the gradient force and depends on the particle's polarizability and the intensity gradient of the electric field.

These two regimes mentioned above are analysed extensively in the original review paper (see the link at the bottom of the page). For the calculation of optical forces acting on particles with arbitrary shapes, the reader is encouraged to study other works [13,14]^[11][12]. Finally, there is an intermediate regime where the particle size is of the same order of magnitude as the wavelength. In this case, the approximations mentioned above cannot be used and, in order to evaluate the forces arising, Maxwell’s stress tensor, which relates the interactions between electromagnetic forces and mechanical momentum [10^[13][14],15], should be used. To handle this complicated mathematical analysis different algorithms have been established, such as the transition matrix (T-matrix) method [16]^[15] and the discrete dipole approximation (DDA) [17]^[16]. Many works have followed various approaches for the calculation of the forces in this regime [18,19,20,21,22,23]^{[17][18][19][20][21][22]}.

Simple calculations can show that for a particle with radius r=100 nm, there is a 53% decrease in the trapping stiffness when the particle's radius decreases to 0.8r. In order to compensate for this effect and increase the trapping constant and the gradient force, we can either increase the intensity of the incident field or focus tighter. However, even though in some cases it is experimentally possible to increase the intensity of the field by a factor of 1,000, the heat accumulation will be huge and eventually destroy the particle, especially if it is a biological sample. On the other hand, the diffraction limit allows focussing of the beam to a certain spot size and this sets a minimum on the particle size that can be successfully trapped. Additional to these limitations, as the particle becomes smaller, the viscous drag reduces and the particle undergoes more intense Brownian motion, making it easier for it to escape from the trap. The use of plasmonic fields (evanescent electrical fields) that don't suffer from the diffraction limit offer a great solution to this problem and make optical tweezers capable of trapping particles in the order of tens of nanometres with very low laser power.

3. Plasmonic Optical Tweezers

Recent advances in the fields of optics and nano-optics have helped to overcome the diffraction limit problem by using evanescent fields instead of propagating ones; these have the intrinsic property of confinement beyond the diffraction limit. A detailed analysis can be found in [33,34]^[23][24]. The current trend is to use metallic nanostructures (see [35]^[25] for a recent review on different platforms) in which surface plasmons can be excited at resonant frequencies and that concentrate the electric field to create highly intense fields, thereby significantly increasing the trapping potential depth that a nanoparticle may experience.

The main disadvantage with plasmonic structures is the conductive nature of metals, which is linked to heat induction and dissipation to the surrounding environment. The excitation of the LSP leads to a frequency-dependent absorption of light by the structures in the metallic thin film, which provides maximum absorption for maximum plasmonic field intensity. The dynamic behaviour of the nanoparticles in and around the optical potential well can be strongly affected by the resultant photothermal effects and various studies have investigated this phenomenon [50,51]^[26][27]. Methods to suppress the heat dissipation have been proposed [52,53]^[28][29] and these could be applied in a synergistic way to mitigate the problem. Additionally, controlled fabrication of the plasmonic structures could enable researchers to take advantage of the self-induced back action effect [54]^[30]. For a more detailed analyses of the principles of plasmonic optical tweezers and the self-induced back action effect the reader is encouraged to read the original review paper (see the link at the bottom of the page).

4. Conclusion

It is interesting to see how a relatively basic idea can be transformed into a very useful technique for manipulating matter, finally leading to the awarding of a Nobel Prize in Physics. Optical tweezers, whether conventional or plasmonic, are now widely used in many fields of research, due to such scientific efforts. A big advantage of optical tweezers is that they are relatively easy and inexpensive to build or to modify according to research needs. Thus, they have found application in various fields such as physics [67]^[31], biosciences [68^[32][33][34],69,70], and chemistry [71]^[35]. In many cases, they serve as a tool to trap or manipulate matter while simultaneously making other measurements, such as Raman spectroscopy of biological samples [72,73,74]^[36][37][38]. There is also an increased interest in exploring the area between particle trapping and atom cooling to study quantum phenomena at the mesoscopic scale [75^[39][40],76], indicating that optical tweezers may even impact the development of quantum-based technologies. Very recently, ground state laser cooling of a subwavelength sized dielectric particle trapped in an optical tweezers has been reported [77]^[41], providing a route to explore topics such as quantum sensing using macrosystems, so it is certainly a very exciting time for further advances in the field.

Of course, there are many open questions and challenges to overcome in order to optimise the techniques so that they can be used to efficiently trap not only particles in the range of less than 10 nm, but also biological samples such as proteins, viruses and DNA for which the treatment as a spherical dielectric particles is inadequate. Although not discussed here, the geometrical shape and material of the trapped object play a significant role in the trapping conditions and, in particular for biomaterials, heating and rapid temperature changes must be taken into consideration. One of the biggest challenges for progress in optical trapping is the ability to fully control and manipulate many trapped nano-objects simultaneously. While this has been achieved for micro-objects by using modulation of the light field, it has yet to be realized in the nanoscale. We can expect to see this barrier surmounted in the near future.