You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 2 by Lindsay Dong and Version 1 by Laith Abualigah.
The optimization algorithms for pathfinding for ground robotics [20,21,22,23,24], aerial vehicles [25,26,27], and underwater vehicles [28,29] includes a wide range of applications. The most well-known applications for autonomous vehicles are obstacle avoidance, path planning, localization, navigation, sensing, and communication, which works on pre-essential maps related to the environment; they also play a vital role in communication relay, aviation industry for surveillance, and loitering dominated missions.
- path planning
- ground vehicle
- underwater vehicle
- UAV
- robotics
- numerical techniques
- bio-inspired techniques
- hybridization
- non-linearity
1. Introduction
The 21st century is the century of autonomy, which accounts for the revolutionary turn in science and technology. The first autonomous guided vehicle was introduced in the 1950s when Barrett Electronics of Northbrook devised a trailer truck that can follow a wire on the ground instead of a truck [1]. Advancement in research and commercial technology made it conceivable for UAVs, robots, and their related application to appear in our daily life activities at an unprecedented rate [2,3][2][3]. For UAVs, Dull Dirty and Dangerous (DDD) missions [4,5,6,7,8,9,10,11][4][5][6][7][8][9][10][11] are the most prominent applications, whereas for robotics, iRobot applications [12] and Self-Driven cars [13] have gained much importance in research area as well as in commercial technology. Such vehicles require autonomous path planning algorithms to be energy/time efficient for their implementation.
The vehicles are equipped with intelligent equipment to localize their position, detect obstacles, and control the motion utilizing suitable navigational techniques to perform navigation tasks. Hence the selection of appropriate navigational techniques is essential for path planning, optimization, and obstacle avoidance. For path planning and motion control of the vehicle, it is envisaged that the vehicle possesses the capability of detecting the obstacle during motion and judge the environment for traveling. So the question becomes, what is expected from such vehicles?
The primary objective of researchers is to develop a real-time autonomous guided vehicle that can travel and can interpret the information gathered from the environment to precisely determine the position and direction towards the goal in both structured and unstructured (obstacle cluttered) environments [14]. The next objective is to achieve all these tasks with the shortest, safest, and most economical route, which ensures the computational and space complexity without anybody’s intervention [15,16][15][16].
Traditionally, path planning involves (a) acquiring information from surroundings, (b) localization of current position, and (c) cognitive mapping helps in taking the required decision satisfying algorithm and executing the task [17]. The autonomous guided vehicle research area lies in formulating computational, algorithmic structures that must be applied to hardware structures utilizing minimum resources. By optimization, further enhancement can be made. An efficient path planning technique of autonomous vehicles can reduce search time and minimize the capital investment of autonomous robots. Optimizing autonomous vehicle path planning involves various practical applications, e.g., disaster management, rescue operations, job performance in industries and factories, agriculture, restaurants, homes, and many others. Due to their applicability and diversity, it has gained importance for researchers to explore the various branches. Autonomous vehicles do not need human assistance for their operation. Any autonomous vehicle needs a path planner to determine the next movement in any indoor/outdoor environment. The definition of path planning differs from researcher to researcher [18,19][18][19].
2. Numerical Techniques
Vehicle trajectory optimization is treated as an optimal control problem [9]. Except for simple problems, optimal control problems must be solved numerically. Numerical methods for solving optimal control problems are divided into three methods: indirect methods, direct methods, and dynamic programming [79][20]. These three methods are then further sub-categorized into different sub-categories, which are graphically depicted in Figure 41 and elaborated in the following section.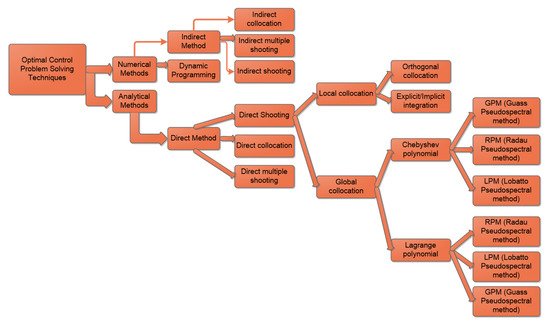
Figure 41.
-
Indirect methods: In the indirect method [81][22], the calculus of variations is used to calculate the first-order optimality conditions of the original optimal control problem. The indirect approach solves the problem indirectly by converting the optimal control problem to a boundary-value problem. As a result, the optimal solution is found in an indirect method by solving a system of differential equations that satisfies endpoint and interior-point conditions.
-
Direct methods: In a direct method, the state and control of the optimal control problem are discretized in some manner, and the problem is transcribed to a non-linear optimization problem or non-linear programming problem (NLP). Direct methods are divided into three categories: direct shooting [82][23], direct multiple shooting [83][24], and collocation. Direct collocation methods utilize a polynomial approximation to the integrated state equations between the nodes, whereas direct shooting methods directly integrate state equations. Arguably, the most powerful methods for solving general optimal control problems are direct collocation methods [79][20]. A direct collocation method is a state and control parameterization method, where the state and control are approximated using a specified functional form. The two most common forms of collocation are local collocation [84][25] and pseudospectral (global orthogonal) collocation [84][25]. In optimal control, local collocation has been employed using one of two categories of discretization: Runge–Kutta methods or the orthogonal collocation method [85,86,87][26][27][28]. In the pseudospectral method [88,89][29][30], the optimal control problem is transcribed to a non-linear programming problem (NLP) by parameterizing the state and control using global polynomials (basis function are Chebyshev or Lagrange polynomials) and collocating the differential-algebraic equations using nodes obtained from a Gaussian quadrature. The collocation points are the roots of an orthogonal polynomial (such as Chebyshev or Legendre polynomials) and/or a linear combination of an orthogonal polynomial and its derivatives.
2.1. Applications to Aerial Vehicles
Researchers utilize different optimal control solvers to determine the optimal trajectories for UAVs in different conditions. Some related work is referenced below:
Using optimal control software, Sachs [90,91,92][31][32][33] calculated an energy-neutral trajectory. Trajectory finders include Graphical Environment for Simulation and Optimization (GESOP) [93][34] and Aerospace Launch Trajectory Optimization Software (ALTOS) [94][35]. ALTOS is an ideal trajectory finder and optimization tool for aeronautical vehicles. This is because, in the presence of multiple local minima, the initial guess might significantly impact the solution’s conclusion. Sachs [95][36] generated energy-neutral paths for trajectory optimization using two different optimization software: BOUNDSCO and TOMP. The first software, ’BOUNDSCO’, uses multiple shooting techniques, while the second, ’TOMP’, uses a parameter optimization strategy to determine optimal control.
Zhao et al. [96,97][37][38] used a collocation strategy to turn the optimal control issue into parameter optimization, which they solved numerically with the software Non-linear Programming Solver” (NPSOL) [98][39]. NPSOL employs a Sequential Quadratic Programming (SQP) technique, where the search direction is a quadratic programming sub-problem solution. The step size is repeatedly chosen at each iteration to create a suitable drop in the augmented Lagrangian merit function. The NPSOL program’s results represent a locally optimal solution to the non-linear programming problem after successful convergence.
2.2. Applications to Ground Vehicles
The concept started with the DARPA Urban Challenge. Later on, numerous controllers have been developed for dealing with the non-linear characteristics of autonomous vehicles. Different controllers has been designed for autonomous guided vehicles, e.g., PID controller [105][40], sliding mode controller [106][41], linear quadratic regulator [107][42], fuzzy logic controller [108][43], backstepping controller [109][44], adaptive control [110][45], and pure pursuit controller [77][46]. Some related work from the literature is referenced below: Thaer et al. [111][47] studied the robotic arm control parameters with numerical solutions involved with the help of the Runge–Kutta method. The non-linear equations are incorporated with formulas of centrifugal effects, Coriolis, and gravitational torques. The method employed was an attempt to mitigate the error involved in the industrial robotic arm, which helps in the increased production system. The acquired results validate the effectiveness of the numerical method and help in analyzing the variations in position and velocity joints. The Runge–Kutta method output perfectly matches with actual velocities. PeiJiang et al. [112][48] used a backpropagation algorithm for the path planning solution in the autonomous robot. The path solution is presented by the numerical method. The concept is employed on the robotic arm manipulator. The industrial robot used for this purpose is the KUKA KR 210 R2700 EXTRA robot. Experiments are performed for validating the path tracking. The mean absolute error for a position is also presented. A comparison between the numerical solution based on the Newton–Raphson algorithm and the path planning solution demonstrates the high-end accuracy and efficiency of the path planning solution. Anirudha et al. [113][49] designed a stability controller by the use of a sums of squares set defined in Lyapunov inequalities. The proposed polynomial controller can be used for handling time-variant dynamics resulting from oscillations involved in trajectory formation. The approach is implemented on an under-actuated double pendulum (Acrobat) and validates that the proposed method performs efficiently. Azali et al. [114][50] solve the path planning issue iteratively using the numerical method. The Laplace equation is used to calculate the potential function. The author came up with a block iterative method known as 4 Point-EG to resolve the trajectory planning. The experiment shows that the proposed method can generate a clear path from the start to the goal position and validates that 4 Point-EG works better compared to previous methods involved in trajectory formation.2.3. Application to Underwater Vehicle
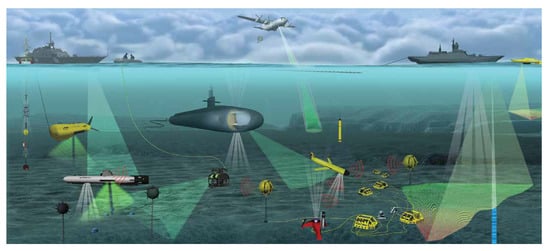
The autonomous underwater vehicle system’s (AUV) navigation and controllers have achieved the same importance as ground and aerial vehicles. They are also known as ocean vehicle navigation. It is equally important to address the related literature involved in the AUV system. Similar to ground and aerial vehicles, autonomous underwater vehicles (AUVs) also need path planning to have an optimal path for their navigation. However, due to data transmission, the sensing range, and power constraints, the sea environment is vulnerable to numerous challenges compared to ground and aerial vehicles. When underwater, it is not easy to communicate effectively because of the continuous fluctuating bandwidth channel. This makes path planning of autonomous underwater vehicles a very challenging task. Motion planning can be categorized into path planning and trajectory planning, and the former can be defined as the course points that the vehicle has to travel to reach the destination point, whereas the time required to complete this journey is formally called trajectory planning. Since no global positioning system (GPS) and no external communication are available underwater, it is hard to acquire information with limited power, and thus, it is hard for an AUV to navigate. Primarily three navigation methods have been suggested [116,117][51][52]: (i) acoustic navigation, (ii) dead-reckoning and inertial navigation systems, and (iii) geophysical navigation. Based on the literature survey, they can be categorized as ‘close-to-bottom navigation’, ‘close to-surface navigation’, and ‘navigation in the mid-depth zone’. Figure 52 shows communication between an autonomous underwater vehicle with unmanned aerial-aquatic vehicle (UAAV) for its navigation purpose.
Figure 52. The communication between the autonomous underwater vehicle with the unmanned aerial-aquatic vehicle [118][53].
3. Bio-Inspired Methods
Siddique et al. [137][54] studied meta-heuristic and nature-inspired algorithms that imitate natural phenomena of natural sciences. Numerous researchers have addressed the ground and aerial vehicle trajectory planning and obstacle avoidance problem using the optimization algorithm that mimics the behavior of living things, such as fish, ants, bees, whales, wolves, and bats [138,139,140,141,142,143][55][56][57][58][59][60]. They are known as non-conventional methods. These algorithms are known as bio-inspired techniques and have been utilized in engineering to solve complex mathematical problems in research [144][61].
Bio-inspired computational-dependent techniques utilized the idea acquired from observing how nature reacts to different things and behaves to solve complex problems, which are considered and characterized with uncertainty and imprecision, to acquire robust solutions at a minimum cost [145][62]. The most prominent bio-inspired algorithms used in trajectory formation and obstacle avoidance for ground robotics include Artificial Neural Networks (ANN), Fuzzy logic, Genetic Algorithm (GA), Artificial Bee Colony (ABC), Simulated Annealing (SA), etc. The newly established algorithms include the Grey Wolf Optimizer (GWO), Moth Flame Optimization, Whale Optimization Algorithm (WOA), Ant Lion Optimizer (ALO), Dragonfly Algorithm, Grasshopper Optimization Algorithm, and Slap Swarm Algorithm. Bio-inspired algorithms are considered better for performing computational-based navigation for path defining as compared to conventional based algorithms, such as the Artificial Potential Field [146][63]. Many researchers integrate these non-conventional algorithms with reinforcement learning to increase the performing capability of ground vehicles in a cluttered obstacle environment. Some techniques are mentioned in Table 41 to give insight to the readers.
The most pertinent conclusion points are summarized as follows:
3.1. Application to Aerial Vehicles
Table 1. Bio-Inspired Algorithms.
| Technique | Seminal Work | Source |
|---|---|---|
| Artificial Neural Network | It is based on Kohonen’s self-organizing maps. | [64][65] |
| Fuzzy Logic | Presented by Professor Lofti Zadeh, in 1965, at the University of California, (refer Figure 6). | [64][65] |
| Artificial Bee Colony Algorithm | Proposed by Karaboga, in 2005, for solving optimization problems. The algorithm mimics the bees colony behavior for the food search. They are divided into three groups: (i) employed bees, (ii) onlooker bees, and (iii) scouts. | [66][67][68] |
| Genetic Algorithm | Derived from evolutionary algorithms, they involve different operators, e.g., mutation, crossover, and selection operator (refer to Figure 7). | [69][70][71][72][73][74][75][76][77] |
| Simulated Annealing | It is a probabilistic method used for finding the global minimum of a function. It is considered the first metaheuristic algorithm inspired by the physical phenomena happening in the solidification of fluids, such as metals. | [78] |
| Grey Wolf Optimizer | Assessing the nature of wolves, researchers were able to formulate mathematical expressions revealing their social behavior in terms of hierarchy distribution of roles in a pack, hunting, the search for prey, and attacking strategies. | [79][80] |
| Moth Flame Optimization | Inspired by the behavior of moths in nature, its popularity lies in its simple implementation and no derivation involvement in the starting phase with fewer parameters, making it easy to implement and flexible for all kinds of applications. | [81][82] |
| Whale Optimization | The hunting behavior hierarchy of whales inspires Whale Optimization. They out-stand because of their hunting strategy. Their foraging behavior is called the bubble-net feeding method. | [83][84][85] |
| AntLion Optimizer | The life cycle of antlions includes two main phases: larvae and adult. Antlions undergo metamorphosis in a cocoon to become adults. They mostly hunt in larvae, and the adulthood period is for reproduction. | [86] |
3.1. Application to Aerial Vehicles
Jesimar et al. [166][87] applied a Genetic Algorithm to path planning for UAVs during the emergency landing situation. Path planning uses a mathematical function, which caters to all constraints. Three different path planning approaches are used: the Genetic Algorithm, greedy heuristic approach, and multi-population algorithm. The greedy approach helps determine the quick solution, whereas the genetic algorithm returns a better quality solution, which helps mitigate the computational time. The methods were validated on a huge dataset with different levels of difficulty. Simulations were carried on the FlightGear simulator, where the behavior of UAVs was checked under different wind directions and velocity directions. The overall statistical analysis demonstrates that combining genetic algorithms with a greedy approach is beneficial for the path planning of UAVs.3.2. Application to Ground Vehicles
Farhad et al. [170][88] attempted to investigate the neural network technique with statistical dimension reduction techniques to execute the navigation task and obstacle avoidance for the robot. The proposed method uses two feed-forward neural networks with a back-propagation learning algorithm. Laser (SICK) is used with a 180∘ range to visualize the surrounding environment. The algorithm checks on real-world and experimental results to prove the efficacy of the proposed algorithm. Lingyan Ran et al. [171][89] worked on vision-based lightweight robot navigation based on uncalibrated spherical images. To improve the trajectory formation, the navigation problem is divided into sub-classification tasks. A 360∘ fisheye camera is introduced for acquiring spherical images in different heading directions. The classification is accomplished using a Convolutional Neural Network (CNN). The CNN tends to predict paths in different directions with high efficiency. Experimental results prove the validity of the proposed method. Ngangbam Herojit et al. [172][90] presented the problem related to the navigation of ground robotics and obstacle avoidance with an Artificial Neural Network. The entire area is divided into five segments, then MLP (Multilayer Perceptron) is activated to find the collision-free path. The simulation proves that the said algorithm gives optimal results for reaching the goal position.3.3. Application to Underwater Vehicles
Carlos Miguel et al. [197][91] worked on underwater glider (UWG) vehicles to ensure their mission success and safety. UWG is considered energy-efficient vehicles, and for performing journeys, they are equipped with sensors that collect data from their surroundings. For a safe journey underwater, the vehicles need to maneuver with a low speed and cater to strong ocean waves, which require extensive path planning. Gliders are often involved in multi-objective functions, e.g., shortest path, obstacle avoidance, energy efficiency, etc. The proposed method involves the non-dominated sorting genetic algorithm II (NSGA-II) to support the motion of gliders in a 3D environment. Glider kinematic simulators coupled with NSGA-II were used to perform experiments for controlling multiple control parameters to perform trajectory optimization. The authors were able to configure the parameters for the desired trajectory and proved to perform a real-time experiment in the ocean.4. Hybrid Algorithms
4.1. Application to Aerial Vehicle
Author Li et al. [207][92] discussed the engineering problems with the help of the Improved Moth Flame Optimization. The proposed algorithm is implemented on a Levy flight trajectory formation. Harun Ilango et al. [208][93] presented the comparison of the Moth Flame Optimization, Bats Optimization Algorithm, and Artificial Bee Colony Algorithm for the landing stage involved in UAV. The objective lies in determining the optimal landing path for UAVs in a minimum amount of time. The empirical results obtained from the Moth Flame Optimization Algorithm take less time to find the optimal path than the other algorithms. Rehan Tariq et al. [209][94] presented the Intelligent Moth Flame Optimization-Based Clustering (IMOC) for drone assistance. The technique is used for maximum coverage using the cluster head approach, which helps find the optimal route. The comparison was made with Ant Colony Optimization (ACO), Grey Wolf Optimization (GWO), and Comprehensive Learning Particle Swarm Optimization (CLPSO). When compared with these algorithms, the proposed algorithm IMOC outperforms the other algorithms in improving the path criterion for UAVs.4.2. Application to Ground Vehicles
Hao Wang et al. [214][95] presented the integration of the Artificial Neural Network with Fuzzy Logic for path planning. The fuzzy neural network can process data in parallel form and can process fuzzy inference functions according to the need for planning the mobile robotics trajectory. The simulations were performed in an unknown environment with static obstacles. The results obtained from simulations show a fast convergence and high efficiency for finding the optimal path. Pengchao Zhang et al. [215][96] proposed that the integration of the traditional algorithm with the heuristic programming algorithm based on AI has beneficial results. The traditional rapidly exploring random tree algorithm is incorporated with a neural network to tune path smoothness and path planning functions. The simulations were performed in real-time to check the feasibility of the improved algorithm, which shows the improved results for handling navigation problems. Buddhadeb Pradhan et al. [216][97] investigates the problem of multi-robots for finding the goal point. Each robot’s motion is controlled by the Particle Swarm Optimization, which the Feeds Forward Neural Network tunes. The coordination algorithm is implemented by a coordinated, cooperative algorithm that maintains the step count of all robots. In the first step, the Artificial Neural Network (ANN) is hybridized with PSO to find the easiest path using acceleration and velocity constraints; the second step, the first and second-order stability analysis, is employed to carry out the convergence. The experiments performed with the proposed algorithm show efficacy and demonstrated promising results. Same as ground vehicles, researchers have also worked on autonomous underwater vehicles.4.3. Application to Underwater Vehicles
Daqi Zhu et al. [219][98] have demonstrated the autonomous underwater vehicles (AUV) in two steps by proposing Glasius Bio-inspired Neural Network (GBNN): (i) the construction of a grid map is done via discretization of 2D environment, (ii) then the neural network is constructed on the grid map. At the final stage, a full path is converged using GBNN, and obstacles are avoided using path templates. The simulations show that AUV can fully cover the environment and shows exceptional maneuverability when stuck in a deadlock situation without delay. The results also demonstrate a low overlapping rate with minimum path planning time when using the proposed algorithm.5. Challenges Involved in Path Planning Methods
Though many researchers have studied the path planning for ground, aerial, and underwater vehicles, no algorithm/technique can guarantee 100% results; moreover, the tendency to get stuck in local/global optima or the incapability to judge the obstacle in front may lead to numerous challenges involved with these techniques. These drawbacks significantly affect the performance of the autonomous guided vehicle. Some challenges are mentioned below: The most used approach for detecting obstacles or planning a path is the deployment of sensors or cameras around any vehicle [236,237][99][100]. However, these sensors’ readings are neither accurate nor reliable as they are integrated with noise, temperature, and system oscillations, etc. This leads to uncertainty in the system output, which causes unintentional error in the output of the algorithm [238][101]. The vehicle may produce oscillations and noise, which affect the real-time efficiency related to the data acquired from the environment [239][102]. Plenty of research has been performed to mitigate and cater the noise occurrence in the vehicle system; however, this is still a challenge. These problems and plenty others widely disturb the implementation of any algorithm in real-time [240][103]. In vision-based algorithms, the problem lies in identifying pairs of points in the same dimension [241][104]. This causes ambiguity in identifying points, which results in inconsistent interpretation of any image [242][105]. Another problem lies in some algorithms that rely on the surrounding environment map for the vehicle to make any decision for navigation. This leads to unnecessary halts in the motion of the vehicle. Baldoni et al. [243][106] demonstrated this challenge through simulations and shows that the generation of the optimal path for any vehicle is complex, and even if the vehicle reaches the desired destination point, it does not produce smooth navigation. ANN may have a lot of advantages, as stated earlier, but they require an extensive data set of the surrounding area for the adjustment of hidden layers [244][107]. The famous backpropagation algorithm has its disadvantages, as it quickly converges to the local minima problem [245][108]. Table 72 depicts the challenges involved in path planning.8
Table 2. Challenges involved in Path Planning.
| Cause | Challenges | Source |
|---|---|---|
| Sensors/camera | The readings form these sensors are not accurate nor reliable as they are integrated with noise, temperature, and system oscillations, etc. This arises uncertainty in the system output, which causes unintentional error in the output of the algorithm. | [99][100][101] |
| Noise occurrence | Plenty of research has been performed to mitigate and cater the noise occurrence in the vehicle system; however, this is still a challenge. These problems and plenty others widely disturb the implementation of any algorithm in real-time. | [103] |
| Vision-Based | The problem lies in identifying pairs of points in the same dimension. This causes ambiguity in identifying points, which results in inconsistent interpretation of any image. | [104][105] |
| ANN | This algorithm has numerous advantages, but they require a large data set of the surrounding area for the adjustment of hidden layers. The famous backpropagation algorithm has its own disadvantages, as it easily converges to the local minima problem. | [107][108] |
5. Conclusions
Trajectory planning is often required in autonomous vehicles. Over the last decade, a lot of research has been performed to address the strengths and challenges involved in autonomous vehicles. This paper comprehensively discussed and summarized the numerical techniques and optimization techniques involved in ground, aerial, and underwater vehicles. Some strengths and challenges are mentioned in Table 93.Table 3. Strengths and Challenges Involved in Hybrid Methods for Ground & Aerial Vehicles.
| Algorithms | Strengths | Challenges | Implementation | Time Complexity |
|---|---|---|---|---|
| Fuzzy Logic | (a) The fuzzy rules can be tuned for desirable requirement [3] | (a) Difficult to create membership functions | Real-time and simulation | T≥0(n2)T≥0(n2) |
| (b) Control logic implementation is easy [109] | ||||
| (c) Can be easily integrated with bio-inspired algorithms [3] | ||||
| Neural Network | (a) Works best in real-time | (a) Difficult to handle buried neuron layers in the network [107] | Real-time and simulation | T≥0(n2) |
| (b) Imitate human control logic easily | (b) Increase in layers increases complexity [107] | |||
| (c) Use of backpropagation results in a local minimum problem [110] | ||||
| (d) Acquiring a large data set in real-time is difficult [107] | ||||
| Genetic Algorithm | (a) Faster convergence rate and optimization capability [111] | (a) Get stuck in local minima problem when environment complexity increase [112] | Simulation | T≥0(n2) |
| (b) Combine well with other algorithms [111] | (b) Produce oscillations in system [113] | |||
| (c) Because of easy implementation integrate well with other algorithms [114] | ||||
| ABC | (a) Requires fewer control parameters [68] | (a) Slow convergence rate [115] | Simulation | T≥0(n2) |
| (b) Requires less computational time [114] | ||||
| (c) Because of easy implementation integrate well with other algorithms [114] | ||||
| Simulated Annealing | (a) Good at approximating global optimum [78] | (a) Slow convergence rate [78] | Simulation | T≥0(n2) |
| GWO | (a) Fast convergence rate [116] | (a) Implementation gets tricky when complex scenarios arise [117] | Simulation | T≥0(n2) |
| (b) Lesser variable involvement [116] (c) Easily integrated with other algorithms [118] | ||||
| Moth Flame | (a) Compared to other algorithms, it produces good solutions in complex scenarios | |||
| AntLion | (a) Produces good results in complex environment [122] | (a) Involvement of a lot of variables makes it difficult to handle when integrated with different algorithms [123] [124] | Simulation | T≥0(n2) |
-
Consolidation of available information: A detailed review of the trajectory planning and optimization is presented from the application point of view on ground, aerial, and underwater vehicles. The DARPA challenge 2007 related to robotics, Lord Rayleigh work related to dynamic soaring in 1883, and some extensions related to the underwater vehicle are elaborated. Algorithms, i.e., numerical techniques for implementing the path planning, are discussed.
-
Survey of trajectory optimization techniques: A comprehensive overview related to optimization algorithms and numerical techniques that have been utilized for performing trajectory formation and its optimization.
-
Problem formulation and generation of optimal trajectories: An explanation of how different algorithms can be integrated to build a mathematical model for planning and the formation of trajectory components can be achieved presented with a literature survey.
-
Limitations and a way forward: Though numerous works review robotics, aerial and underwater vehicle systems have been presented together with optimization techniques and numerical methods, and it has been observed no single algorithm produces desired results or accurate output; therefore, a hybridization of different algorithms has been used by researchers. Two optimization algorithms or two numerical methods together can be integrated, or a mix and match of techniques can be achieved for obtaining the desired characteristics results.
| [ |
| 119 |
| ] | ||||
| (a) Has premature convergence rate | [ | 120] | Simulation | T≥0(n2) |
| WOA | (a) Easy implementation with fast convergence rate [121] | (a) Difficult to handle in a complex environment [58] | Simulation | T≥0(n2) |
References
- Li, S.; Yan, J.; Li, L. Automated guided vehicle: The direction of intelligent logistics. In Proceedings of the 2018 IEEE International Conference on Service Operations and Logistics, and Informatics (SOLI), Singapore, 31 July–2 August 2018; pp. 250–255.
- Fanti, M.P.; Mangini, A.M.; Pedroncelli, G.; Ukovich, W. A decentralized control strategy for the coordination of AGV systems. Control Eng. Pract. 2018, 70, 86–97.
- Zhong, M.; Yang, Y.; Dessouky, Y.; Postolache, O. Multi-AGV scheduling for conflict-free path planning in automated container terminals. Comput. Ind. Eng. 2020, 142, 106371.
- Masłowski, A. Training in Military Robotics and EOD Unmanned Systems. 2014. Available online: https://www.eodcoe.org/files/en/events/nato-eod-demonstrations-trials-2014/3-nato_eod_trencin-09_2014-maslowski-opt.pdf (accessed on 6 August 2020).
- Vassev, E.; Hinchey, M. Autonomy Requirements Engineering for Space Missions; Springer: Berlin/Heidelberg, Germany, 2014.
- Gao, W.; Wang, W.; Zhu, H.; Zhao, S.; Huang, G.; Du, Z. Irradiation test and hardness design for mobile rescue robot in nuclear environment. Ind. Robot. Int. J. Robot. Res. Appl. 2019, 46, 851–862.
- Mir, I.; Akhtar, S.; Eisa, S.; Maqsood, A. Guidance and control of standoff air-to-surface carrier vehicle. Aeronaut. J. 2019, 123, 283–309.
- Mir, I.; Taha, H.; Eisa, S.A.; Maqsood, A. A controllability perspective of dynamic soaring. Nonlinear Dyn. 2018, 94, 2347–2362.
- Mir, I.; Eisa, S.A.; Maqsood, A. Review of dynamic soaring: Technical aspects, nonlinear modeling perspectives and future directions. Nonlinear Dyn. 2018, 94, 3117–3144.
- Mir, I.; Maqsood, A.; Eisa, S.A.; Taha, H.; Akhtar, S. Optimal morphing–augmented dynamic soaring maneuvers for unmanned air vehicle capable of span and sweep morphologies. Aerosp. Sci. Technol. 2018, 79, 17–36.
- Mir, I.; Eisa, S.A.; Taha, H.E.; Maqsood, A.; Akhtar, S.; Islam, T.U. A stability perspective of bio-inspired UAVs performing dynamic soaring optimally. Bioinspir. Biomim. 2021.
- Fink, J.; Bauwens, V.; Kaplan, F.; Dillenbourg, P. Living with a vacuum cleaning robot. Int. J. Soc. Robot. 2013, 5, 389–408.
- Häne, C.; Heng, L.; Lee, G.H.; Fraundorfer, F.; Furgale, P.; Sattler, T.; Pollefeys, M. 3D visual perception for self-driving cars using a multi-camera system: Calibration, mapping, localization, and obstacle detection. Image Vis. Comput. 2017, 68, 14–27.
- Zhou, C.; Huang, B.; Fränti, P. A survey of motion planning algorithms for intelligent robotics. arXiv 2021, arXiv:2102.02376.
- Contreras-Cruz, M.A.; Ayala-Ramirez, V.; Hernandez-Belmonte, U.H. Mobile robot path planning using artificial bee colony and evolutionary programming. Appl. Soft Comput. 2015, 30, 319–328.
- Littlefield, Z.; Bekris, K.E. Efficient and asymptotically optimal kinodynamic motion planning via dominance-informed regions. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9.
- Ganeshmurthy, M.; Suresh, G. Path planning algorithm for autonomous mobile robot in dynamic environment. In Proceedings of the 2015 3rd International Conference on Signal Processing, Communication and Networking (ICSCN), Chennai, India, 26–28 March 2015; pp. 1–6.
- Choset, H.M.; Hutchinson, S.; Lynch, K.M.; Kantor, G.; Burgard, W.; Kavraki, L.E.; Thrun, S.; Arkin, R.C. Principles of Robot Motion: Theory, Algorithms, and Implementation; MIT Press: Cambridge, MA, USA, 2005.
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006.
- Rao, A.V. A survey of numerical methods for optimal control. Adv. Astronaut. Sci. 2009, 135, 497–528.
- Bellman, R. Dynamic Programming. In New Jersey Google Scholar; Princeton University Press: Princeton, NJ, USA, 1957.
- Bellman, R. Dynamic programming treatment of the travelling salesman problem. J. ACM (JACM) 1962, 9, 61–63.
- Gerdts, M. Direct shooting method for the numerical solution of higher-index DAE optimal control problems. J. Optim. Theory Appl. 2003, 117, 267.
- Cannataro, B.Ş.; Rao, A.V.; Davis, T.A. State-defect constraint pairing graph coarsening method for Karush–Kuhn–Tucker matrices arising in orthogonal collocation methods for optimal control. Comput. Optim. Appl. 2016, 64, 793–819.
- Huntington, G.T.; Rao, A.V. Comparison of global and local collocation methods for optimal control. J. Guid. Control. Dyn. 2008, 31, 432.
- Schwartz, A.L. Theory and Implementation of Numerical Methods Based on Runge-Kutta Integration for Solving Optimal Control Problems. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1996.
- Reddien, G. Collocation at Gauss points as a discretization in optimal control. SIAM J. Control Optim. 1979, 17, 298–306.
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Comput. Ind. Eng. 2021, 157, 107250.
- Rao, A.V.; Benson, D.A.; Darby, C.; Patterson, M.A.; Francolin, C.; Sanders, I.; Huntington, G.T. Algorithm 902: Gpops, a matlab software for solving multiple-phase optimal control problems using the gauss pseudospectral method. ACM Trans. Math. Softw. (TOMS) 2010, 37, 22.
- Darby, C.L.; Hager, W.W.; Rao, A.V. An hp-adaptive pseudospectral method for solving optimal control problems. Optim. Control Appl. Methods 2011, 32, 476–502.
- Sachs, G.; da Costa, O. Optimization of dynamic soaring at ridges. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Austin, TX, USA, 11–14 August 2003; pp. 11–14.
- Sachs, G. Minimum shear wind strength required for dynamic soaring of albatrosses. IBIS 2005, 147, 1–10.
- Sachs, G.; Mayrhofer, M. Shear wind strength required for dynamic soaring at ridges. Tech. Soar. 2001, 25, 209–215.
- Well, K. Graphical environment for simulation and optimization. In Department of Optimization, Guidance, and Control; Springer: Stuttgart, Germany, 2002.
- Wiegand, A. ASTOS User Manual. Unterkirnach Ger. Astos Solut. GmbH 2010, 17, 34–52.
- Sachs, G.; Knoll, A.; Lesch, K. Optimal utilization of wind energy for dynamic soaring. Tech. Soar. 1991, 15, 48–55.
- Zhao, Y.J. Optimal patterns of glider dynamic soaring. Optim. Control Appl. Methods 2004, 25, 67–89.
- Zhao, Y.J.; Qi, Y.C. Minimum fuel powered dynamic soaring of unmanned aerial vehicles utilizing wind gradients. Optim. Control Appl. Methods 2004, 25, 211–233.
- Gill, P.E.; Murray, W.; Saunders, M.A.; Wright, M.H. User’s Guide for NPSOL (version 4.0): A Fortran Package for Nonlinear Programming; Technical Report; Stanford Univ Ca Systems Optimization LAB: Stanford, CA, USA, 1986.
- Li, X.; Luo, C.; Xu, Y.; Li, P. A Fuzzy PID controller applied in AGV control system. In Proceedings of the 2016 International Conference on Advanced Robotics and Mechatronics (ICARM), Macau, China, 18–20 August 2016; pp. 555–560.
- Matveev, A.S.; Wang, C.; Savkin, A.V. Real-time navigation of mobile robots in problems of border patrolling and avoiding collisions with moving and deforming obstacles. Robot. Auton. Syst. 2012, 60, 769–788.
- Li, Y.; Wang, X.N.; Li, S.J.; Zhu, J. LQR based Trajectory Tracking Control for Forked AGV. In Applied Mechanics and Materials; Trans Tech Publications Ltd: Baech, Switzerland, 2014; Volume 577, pp. 447–451.
- Castillo, O.; Aguilar, L.T.; Cárdenas, S. Fuzzy Logic Tracking Control for Unicycle Mobile Robots. Eng. Lett. 2006, 13, 1–5.
- Dumitrascu, B.; Filipescu, A.; Minzu, V. Backstepping control of wheeled mobile robots. In Proceedings of the 15th International Conference on System Theory, Control and Computing, Sinaia, Romania, 14–16 October 2011; pp. 1–6.
- Gul, F.; Alhady, S.S.N.; Rahiman, W. A review of control algorithm for autonomous guided vehicle. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 552–562.
- Gul, F.; Rahiman, W. An Integrated approach for Path Planning for Mobile Robot Using Bi-RRT. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 697, p. 012022.
- Alsultan, T.; Ali, H.M.; Hamid, Q.Y. A numerical approach for solving problems in robotic arm movement. Prod. Manuf. Res. 2018, 6, 385–395.
- Yuan, P.; Su, F.; Shi, Z.; Wang, T.; Chen, D. Autonomous path planning solution for industrial robot manipulator using backpropagation algorithm. Adv. Mech. Eng. 2015, 7, 1687814015619768.
- Majumdar, A.; Ahmadi, A.A.; Tedrake, R. Control design along trajectories with sums of squares programming. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4054–4061.
- Saudi, A.; Sulaiman, J. Numerical technique for robot path planning using four Point-EG iterative method. In Proceedings of the 2010 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 15–17 June 2010; Volume 2, pp. 831–836.
- Leonard, J.J.; Bennett, A.A.; Smith, C.M.; Jacob, H.; Feder, S. Autonomous Underwater Vehicle Navigation. MIT Marine Robotics Laboratory Technical Memorandum. Citeseer. 1998. Available online: www.cml.mit.edu/~jleonard/pubs/techreport981.pdf (accessed on 6 August 2020).
- Leonard, J.J.; Bahr, A. Autonomous underwater vehicle navigation. In Springer Handbook of Ocean Engineering; Springer: Berlin/Heidelberg, Germany, 2016; pp. 341–358.
- Bedwell, I. Australian Sonar Transducer Technology. Available online: https://www.academia.edu/download/62864992/Bedwell_Australian_Sonar_Transducer_Technology_120200407-14290-1e51qex.pdf (accessed on 20 November 2013).
- Siddique, N.; Adeli, H. Nature inspired computing: An overview and some future directions. Cogn. Comput. 2015, 7, 706–714.
- Zhang, Y.; Guan, G.; Pu, X. The robot path planning based on improved artificial fish swarm algorithm. Math. Probl. Eng. 2016, 2016, 3297585.
- Wang, H.J.; Fu, Y.; Zhao, Z.Q.; Yue, Y.J. An Improved Ant Colony Algorithm of Robot Path Planning for Obstacle Avoidance. J. Robot. 2019, 2019, 6097591.
- Saffari, M.; Mahjoob, M. Bee colony algorithm for real-time optimal path planning of mobile robots. In Proceedings of the 2009 Fifth International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control, Famagusta, North Cyprus, 2–4 September 2009; pp. 1–4.
- Dao, T.K.; Pan, T.S.; Pan, J.S. A multi-objective optimal mobile robot path planning based on whale optimization algorithm. In Proceedings of the2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 337–342.
- Tsai, P.W.; Dao, T.K. Robot path planning optimization based on multiobjective grey wolf optimizer. In International Conference on Genetic and Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2016; pp. 166–173.
- Guo, J.; Gao, Y.; Cui, G. The path planning for mobile robot based on bat algorithm. Int. J. Autom. Control 2015, 9, 50–60.
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2010.
- Chaturvedi, D. Soft Computing Techniques and Their Applications. In Mathematical Models, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 31–40.
- Wang, P.; Gao, S.; Li, L.; Sun, B.; Cheng, S. Obstacle avoidance path planning design for autonomous driving vehicles based on an improved artificial potential field algorithm. Energies 2019, 12, 2342.
- Surmann, H.; Kanstein, A.; Goser, K. Self-Organizing and Genetic Algorithms for an Automatic Design of Fuzzy Control and Decision Systems. In Proceedings of the EUFIT’93; Citeseer: Princeton, NJ, USA, 1993.
- Payne, D.; Stern, J. Wavelength-switched passively coupled single-mode optical network. In Proceedings of the IOOC-ECOC, Venezia, Italy, 1–4 October 1985; Volume 85, p. 585.
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132.
- Baykasoğlu, A.; Özbakır, L.; Tapkan, P. Artificial Bee Colony Algorithm and Its Application to Generalized Assignment Problem Swarm Intelligence Focus on Ant and Particle Swarm Optimization. 17 December 2007. Available online: www.10.5772/5101 (accessed on 6 August 2021).
- Kamil, R.T.; Mohamed, M.J.; Oleiwi, B.K. Path Planning of Mobile Robot Using Improved Artificial Bee Colony Algorithm. Eng. Technol. J. 2020, 38, 1384–1395.
- Ismail, A.; Sheta, A.; Al-Weshah, M. A mobile robot path planning using genetic algorithm in static environment. J. Comput. Sci. 2008, 4, 341–344.
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998.
- Xin, D.; Hua-hua, C.; Wei-kang, G. Neural network and genetic algorithm based global path planning in a static environment. J. Zhejiang Univ.-Sci. A 2005, 6, 549–554.
- Li, J.; Deng, G.; Luo, C.; Lin, Q.; Yan, Q.; Ming, Z. A hybrid path planning method in unmanned air/ground vehicle (UAV/UGV) cooperative systems. IEEE Trans. Veh. Technol. 2016, 65, 9585–9596.
- Lee, J.; Kang, B.Y.; Kim, D.W. Fast genetic algorithm for robot path planning. Electron. Lett. 2013, 49, 1449–1451.
- Tian, L.; Collins, C. An effective robot trajectory planning method using a genetic algorithm. Mechatronics 2004, 14, 455–470.
- Han, W.G.; Baek, S.M.; Kuc, T.Y. Genetic algorithm based path planning and dynamic obstacle avoidance of mobile robots. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 3, pp. 2747–2751.
- Châari, I.; Koubaa, A.; Bennaceur, H.; Trigui, S.; Al-Shalfan, K. SmartPATH: A hybrid ACO-GA algorithm for robot path planning. In Proceedings of the 2012 IEEE congress on evolutionary computation, Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8.
- Geisler, T.; Manikas, T.W. Autonomous robot navigation system using a novel value encoded genetic algorithm. In Proceedings of the 2002 45th Midwest Symposium on Circuits and Systems, 2002, MWSCAS-2002, Tulsa, OK, USA, 4–7 August 2002; Volume 3, p. III.
- Liu, K.; Zhang, M. Path planning based on simulated annealing ant colony algorithm. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016; Volume 2, pp. 461–466.
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61.
- Zhang, S.; Zhou, Y.; Li, Z.; Pan, W. Grey wolf optimizer for unmanned combat aerial vehicle path planning. Adv. Eng. Softw. 2016, 99, 121–136.
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249.
- Hussien, A.G.; Amin, M.; Abd El Aziz, M. A comprehensive review of moth-flame optimisation: Variants, hybrids, and applications. J. Exp. Theor. Artif. Intell. 2020, 32, 705–725.
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67.
- Watkins, W.A.; Schevill, W.E. Aerial observation of feeding behavior in four baleen whales: Eubalaena glacialis, Balaenoptera borealis, Megaptera novaeangliae, and Balaenoptera physalus. J. Mammal. 1979, 60, 155–163.
- Goldbogen, J.A.; Friedlaender, A.S.; Calambokidis, J.; Mckenna, M.F.; Simon, M.; Nowacek, D.P. Integrative approaches to the study of baleen whale diving behavior, feeding performance, and foraging ecology. BioScience 2013, 63, 90–100.
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98.
- Silva Arantes, J.d.; Silva Arantes, M.d.; Motta Toledo, C.F.; Júnior, O.T.; Williams, B.C. Heuristic and genetic algorithm approaches for UAV path planning under critical situation. Int. J. Artif. Intell. Tools 2017, 26, 1760008.
- Shamsfakhr, F.; Bigham, B.S. A neural network approach to navigation of a mobile robot and obstacle avoidance in dynamic and unknown environments. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 1629–1642.
- Ran, L.; Zhang, Y.; Zhang, Q.; Yang, T. Convolutional neural network-based robot navigation using uncalibrated spherical images. Sensors 2017, 17, 1341.
- Singh, N.H.; Thongam, K. Neural network-based approaches for mobile robot navigation in static and moving obstacles environments. Intell. Serv. Robot. 2019, 12, 55–67.
- Lucas, C.; Hernández-Sosa, D.; Greiner, D.; Zamuda, A.; Caldeira, R. An Approach to Multi-Objective Path Planning Optimization for Underwater Gliders. Sensors 2019, 19, 5506.
- Li, Y.; Zhu, X.; Liu, J. An Improved Moth-Flame Optimization Algorithm for Engineering Problems. Symmetry 2020, 12, 1234.
- Ilango, H.S.; Ramanathan, R. A Performance Study of Bio-Inspired Algorithms in Autonomous Landing of Unmanned Aerial Vehicle. Procedia Comput. Sci. 2020, 171, 1449–1458.
- Tariq, R.; Iqbal, Z.; Aadil, F. IMOC: Optimization Technique for Drone-Assisted VANET (DAV) Based on Moth Flame Optimization. Wirel. Commun. Mob. Comput. 2020, 2020, 8860646.
- Wang, H.; Duan, J.; Wang, M.; Zhao, J.; Dong, Z. Research on robot path planning based on fuzzy neural network algorithm. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 1800–1803.
- Zhang, P.; Xiong, C.; Li, W.; Du, X.; Zhao, C. Path planning for mobile robot based on modified rapidly exploring random tree method and neural network. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418784221.
- Pradhan, B.; Nandi, A.; Hui, N.B.; Roy, D.S.; Rodrigues, J.J. A Novel Hybrid Neural Network-Based Multirobot Path Planning With Motion Coordination. IEEE Trans. Veh. Technol. 2019, 69, 1319–1327.
- Zhu, D.; Tian, C.; Sun, B.; Luo, C. Complete coverage path planning of autonomous underwater vehicle based on GBNN algorithm. J. Intell. Robot. Syst. 2019, 94, 237–249.
- Lagisetty, R.; Philip, N.; Padhi, R.; Bhat, M. Object detection and obstacle avoidance for mobile robot using stereo camera. In Proceedings of the 2013 IEEE International Conference on Control Applications (CCA), Hyderabad, India, 28–30 August 2013; pp. 605–610.
- Fulgenzi, C.; Spalanzani, A.; Laugier, C. Dynamic obstacle avoidance in uncertain environment combining PVOs and occupancy grid. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1610–1616.
- Michels, J.; Saxena, A.; Ng, A.Y. High speed obstacle avoidance using monocular vision and reinforcement learning. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 593–600.
- Matveev, A.S.; Hoy, M.C.; Savkin, A.V. A globally converging algorithm for reactive robot navigation among moving and deforming obstacles. Automatica 2015, 54, 292–304.
- Seraji, H.; Howard, A. Behavior-based robot navigation on challenging terrain: A fuzzy logic approach. IEEE Trans. Robot. Autom. 2002, 18, 308–321.
- Sharma, P.S.; Chitaliya, D. Obstacle avoidance using stereo vision: A survey. Int. J. Innov. Res. Comput. Commun. Eng. 2015, 3, 24–29.
- Typiak, A. Use of laser rangefinder to detecting in surroundings of mobile robot the obstacles. In Proceedings of the Symposium on Automation and Robotics in Construction, Vilnius, Lithuania, 26–29 June 2008; pp. 26–29.
- Baldoni, P.D.; Yang, Y.; Kim, S.Y. Development of efficient obstacle avoidance for a mobile robot using fuzzy Petri nets. In Proceedings of the 2016 IEEE 17th International Conference on Information Reuse and Integration (IRI), Pittsburgh, PA, USA, 28–30 July 2016; pp. 265–269.
- Yang, J.; Chen, P.; Rong, H.J.; Chen, B. Least mean p-power extreme learning machine for obstacle avoidance of a mobile robot. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1968–1976.
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41.
- Cherroun, L.; Boumehraz, M.; Kouzou, A. Mobile Robot Path Planning Based on Optimized Fuzzy Logic Controllers. In New Developments and Advances in Robot Control; Springer: Berlin/Heidelberg, Germany, 2019; pp. 255–283.
- Chhotray, A.; Parhi, D.R. Navigational control analysis of two-wheeled self-balancing robot in an unknown terrain using back-propagation neural network integrated modified DAYANI approach. Robotica 2019, 37, 1346–1362.
- Naazare, M.; Ramos, D.; Wildt, J.; Schulz, D. Application of Graph-based Path Planning for UAVs to Avoid Restricted Areas. In Proceedings of the 2019 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Würzburg, Germany, 2–4 September 2019; pp. 139–144.
- Burchardt, H.; Salomon, R. Implementation of path planning using genetic algorithms on mobile robots. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1831–1836.
- Su, K.; Wang, Y.; Hu, X. Robot path planning based on random coding particle swarm optimization. Int. J. Adv. Comput. Sci. Appl. 2015, 6, 58–64.
- Darwish, A.H.; Joukhadar, A.; Kashkash, M. Using the Bees Algorithm for wheeled mobile robot path planning in an indoor dynamic environment. Cogent Eng. 2018, 5, 1426539.
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57.
- Wu, H.S.; Zhang, F.M. Wolf pack algorithm for unconstrained global optimization. Math. Probl. Eng. 2014, 2014.
- Mittal, N.; Singh, U.; Sohi, B.S. Modified grey wolf optimizer for global engineering optimization. Appl. Comput. Intell. Soft Comput. 2016, 2016, 7950348.
- Liu, C.; Yan, X.; Liu, C.; Wu, H. The wolf colony algorithm and its application. Chin. J. Electron. 2011, 20, 212–216.
- Jalali, S.M.J.; Khosravi, A.; Kebria, P.M.; Hedjam, R.; Nahavandi, S. Autonomous robot navigation system using the evolutionary multi-verse optimizer algorithm. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 1221–1226.
- Jalali, S.M.J.; Hedjam, R.; Khosravi, A.; Heidari, A.A.; Mirjalili, S.; Nahavandi, S. Autonomous robot navigation using moth-flame-based neuroevolution. In Evolutionary Machine Learning Techniques; Springer: Berlin/Heidelberg, Germany, 2020; pp. 67–83.
- Chhillar, A.; Choudhary, A. Mobile Robot Path Planning Based Upon Updated Whale Optimization Algorithm. In Proceedings of the 2020 10th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 29–31 January 2020; pp. 684–691.
- Zhenxing, Z.; Rennong, Y.; Huanyu, L.; Yuhuan, F.; Zhenyu, H.; Ying, Z. Antlion optimizer algorithm based on chaos search and its application. J. Syst. Eng. Electron. 2019, 30, 352–365.
- Rout, A.; Mahanta, G.B.; Bbvl, D.; Biswal, B.B. Kinematic and Dynamic Optimal Trajectory Planning of Industrial Robot Using Improved Multi-objective Ant Lion Optimizer. J. Inst. Eng. (India) Ser. 2020, 101, 559–569.
- Gul, F.; Rahiman, W.; Alhady, S.N.; Ali, A.; Mir, I.; Jalil, A. Meta-heuristic approach for solving multi-objective path planning for autonomous guided robot using PSO—GWO optimization algorithm with evolutionary programming. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 7873–7890.
More
