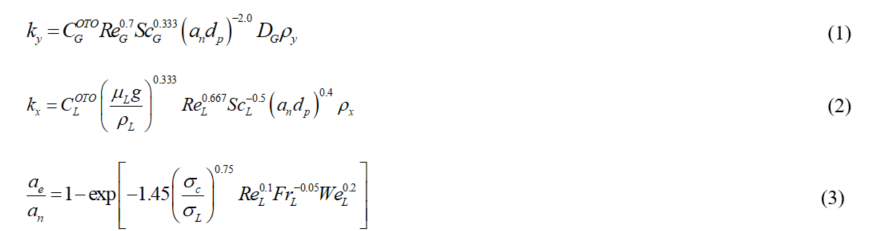This review provides a thorough analysis of the most famous mass transfer models for random and structured packed-bed columns used in absorption/stripping and distillation processes, providing an overview of the equations to calculate the mass transfer parameters, i.e.: gas-side coefficient per unit surface ky [kmol·m-2·s-1], liquid-side coefficient per unit surface kx [kmol·m-2·s-1], interfacial packing area ae [m2·m-3], which constitute the ingredients to assess the mass transfer rate of packed-bed columns. This work also provides the ranges of model validity and applicability together with their main pros and cons and the criticalities behind these models, which mostly rely on the assessment of fluid-dynamics parameters such as liquid film thickness, liquid hold-up and interfacial area, or the real liquid paths or any mal-distributions flow.
- separation technologies
- unit operations
- gas-liquid mass transfer
- mass transfer review
- mass transfer coefficients for packed columns
- structured packing
- random packing
- absorption column
- stripping column
- distillation column
- cooling tower
1. Introduction
Packed columns are used extensively in chemical process industries, especially in the field of distillation, evaporation, humidification, gas absorption and desorption.
Random elements have been used as packing units since the beginning of the 20th century and they consist of discrete structural elements that are randomly dumped in the contact vessel [1][2]. Since the second and half of the 1980s structured packings entered the chemical industry market. Structured packings are made of corrugated metal or plastic sheets or wire meshes that are placed vertically into the column as blocks of assembled layers. These packings have gained a fast-growing spread in the process industries, as they can provide higher capacity and interfacial area with high separation efficiency, small scale-up limits and much lower pressure drops than random packings [3]. These features make the structured packings more convenient for those applications requiring lower pressure drops and smaller space requirements.
The proper design and rating of packed towers requires accurate models to predict pressure drops and mass-transfer coefficients. Several models have been proposed in the past to estimate the mass transfer coefficients of packings. These models are normally semi-empiric and require assessment of calibration parameters to account for the specific geometry of the packing. Their utilization in process design tend to provide different estimation of the mass transfer coefficient, that will translate in a different degree of accuracy in the estimation of column height and in a different bias for the process design.
The history of mass transfer coefficients correlations for packing towers has more than 60 years. The first models of large diffusion in the unit operation textbooks were the Cornell's method [4] for Raschig rings and Berl saddles, the McCabe et al. method [5] experimentally based approach and the Onda's method [6]. Years later, Bolles and Fair (1979) [7] have extended the Cornell's method also for Pall ring and Intalox saddles. Instead, Bravo et al. [8] proposed a new model for mass transfer estimation in random packed columns.
For structured packings, one of the first models adopted in several textbook was provided by Bravo et al. [8] and modified by Shi and Mersmann [9] which revised the estimation of interfacial surface area of the original model. These were based on semi-empirical equations, two-films theory for estimation of gas-side coefficient and the penetration theory for the liquid-side coefficient. After their pioneering work, Bravo et al. [10] reported a revised version of their model adding liquid hold-up and film thickness data as physical parameters and introducing two correction factors: the first to correct the total liquid hold-up and the second to take into account the surface renewal of the packing.
One year later, Billet and Schultes [11] proposed a descriptive model using the theory of penetration for the calculation of both gas and liquid coefficients, introducing corrective factors for both ky and kx equations. The Authors provided a number of calibration parameters based on extensive experimental tests conducted under specific operating conditions (different gas and liquid loads, pressure and temperature and several chemical-physical properties of gas and liquid) and specific packing both random and structured.
Other Authors provided a second generation of models following either the approach proposed by Bravo et al. [10] or Billet and Schultes [11][12], always considering suitable calibration parameters. Brunazzi and Paglianti [13] adopted the theory of mixing factor for liquid-side coefficient, while the Chilton and Colburn analogy was used by Olujić et al. [14] in the Delft model to estimate gas-side coefficients
Lately, Hanley and Chen [15] used a new data fitting procedure derived from Bravo and Billet and Schultes experiments [10][11][12], which were adopted as reference mass transfer models for distillation and absorption columns in the ASPEN PLUS software. Hanley and Chen [15] proposed a new set of equations based on dimensionless groups, fitting parameters and functional dependencies found for specific random and structured packing classes.
This work aims to provide a comprehensive and critical overview of the most recognized models in the last decades for predicting the gas-side (ky) and the liquid-side (kx) mass-transfer coefficients and the interfacial areas (ae) for packed towers with random and structured packing. The work has carefully selected and examined the most successful correlation models and adopted in the open scientific literature [16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39] also providing the ranges of models validity and applicability together with their main pros and cons, to help the reader in selecting the most suitable one for specific packing/application. New experimental findings and modeling approaches available in the last 20 years literaure to refine the proposed correlations are also reported.
2. Mass transfer models for packed-bed columns
The works reported in this document are based on different theories and experimental evidences on mass-transfer for packed columns developed by several Authors in the last fifty years. The models are suitable for specific types of random and structured packings and provide the predictive correlations for liquid and gas mass-transfer coefficients (kx and ky) per surface unit [kmol·m-2·s-1] and wet effective surface area to the mass transfer (ae, [m2·m-3]). The model equations are reported in Table 1.
Table 1. Equations of mass transfer predictive correlations to calculate liquid and gas mass transfer coefficients and wet surface area for packed columns. The details of the model parameters are reported in the List of Symbols.
|
Mass transfer models |
Equations |
|
Onda et al. (1968) for random packing |
|
|
Bravo et al. (1985) for structured packing |
|
|
Bravo et al. (1992) for structured packing |
|
|
Billet and Schultes (1993) for random & structured packing |
|
|
Brunazzi and Paglianti (1997) for structured packing |
|
|
Olujić et al. (2004) for structured packing |
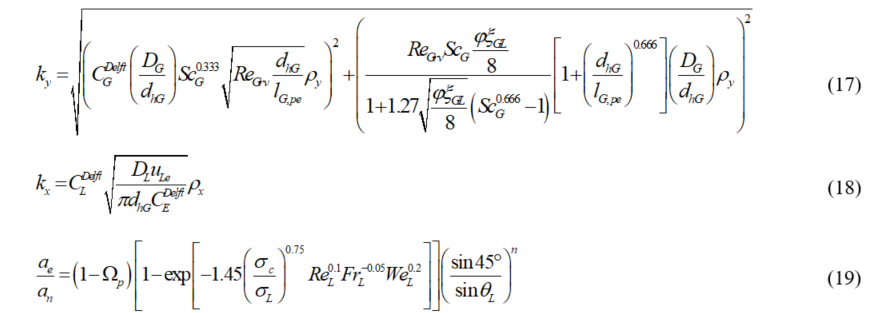
|
|
Hanley and Chen (2012) for random & structured packing |
|
The model parameters contained in the equations from Table 1 are discussed in detail with complete formulations in Flagiello et al. [40]. The equations also included a series of model fitting parameters to adapt their correlations to specific types and models of packings. These constant values are reported in Flagiello et al. [40].
3. Model comparison and field of application
In the Table 2 are shown the field of application of each model in use for different packing/application together with the different operating conditions, the number of fitting model parameters required and the estimated model prediction error with respect to the experimental values of kxae and kyae or HETPs.
Table 2. Summary of the validity and applicability ranges of the correlations examined in this Section, based on packing/application, experimental conditions, number of fitting parameters and estimated error adopted by the authors for their formulations.
|
Models |
Application |
Column Size |
Operating Conditions |
Packing Type |
Error |
Fitting Param. |
||||
|
D, m |
Z, m |
P, atm |
T, K |
FG, Pa0.5 |
FL, m/h |
|||||
|
OTO |
Absorption/ Desorption |
0.06-0.1 |
0.1-0.3 |
1.0 |
293-298 |
0.75-2.95 |
up to 295 |
Raschig rings Berl saddles Spheres, Rods |
±30%1 |
2 |
|
BRF |
Distillation |
0.43 |
3.0 |
0.33-4.14 |
334-427 |
0.6-3.2 |
9.0-35 |
Sulzer BX |
47%2 8.0%3 |
2 |
|
SRP |
Distillation Absorption |
0.43 |
3.0 |
0.33-20.4 |
334-427 |
0.2-3.6 |
9.0-35 |
Sulzer BX Gempak 2A Gempak 2AT Intalox 2T Flexipac 2Y Maxpak Mellapak: 250Y,350Y, 500Y |
±24%4 |
4 |
|
BS |
Distillation Absorption/ Desorption |
0.06-1.4 |
0.15-3.95 |
0.033-1.0 |
288-407 |
0.01-2.77 |
up to 118.20 |
See Billet and Schultes [11,12] |
±8.3%5 ±12.4%6 |
2 |
|
BP |
Absorption/ Desorption |
0.05-1.0 |
0.42-1.89 |
1.00 |
298 |
0.5-3.1 |
1.2-79.2 |
Sulzer BX Mellapak: 125Y,250Y, 500Y |
±15%5 ±19%6 |
4 |
|
Delft |
Distillation |
0.2-1.4 |
3.4-6.0 |
0.33-4.14 |
334-427 |
0.5-4.0 |
9.0-35 |
Montz: B1-250,B1-400 B1-250.60 B1-400.60 BSH-400 BSH-400.60 |
±12%4 |
3 |
|
HC |
Distillation Absorption/ Desorption |
See BRF, SRP and BS model |
±10%4 |
10 (random) 11/12 (structur.) |
||||||
Note: 1 refers to the range errors of the two coefficients; 2 refers to the average error with respect to the experimental HETPs using original ae equation; 3 refers to the average error with respect to the experimental HETPs using revisited ae equation; 4 refers to the range error with respect to the experimental HETPs; 5 refers to the range error for kx coefficient; 6 refers to the range error for ky coefficient.
The most dated and used correlations in the textbooks are the models of Onda et al. [6] for random packing and Bravo et al. [8] for structured packing. The Onda model was tested with Raschig rings, Berl saddles, Spheres and Rods in different sizes and materials in absorption and desorption processes, while Bravo model was characterized only with Sulzer BX gauze-type structured packing in distillation applications. The correlations of Onda need two fitting parameters for the gas-side and liquid-side coefficient and provide a very high error from experiments in the range ±30%. Also the correlations of Bravo requires only two parameters for the coefficients and even if fluid-dynamics parameters, i.e. the liquid hold-up and film thickness are not taken into account, the Bravo model records an average error of approximately 8% from experimental HETP values using the revised equation for the interfacial area. Despite this, on the other hand, the field of applicability for this model is very limited.
The correlations of Bravo et al. [10] or SRP and Billet and Schultes [11] are valid for different types of packing. In particular, the SRP model has been tested in distillation applications, also for column pressure higher than 1 atm, for a fair number of structured packing (Koch-Glitsch, Sulzer, Jaeger and Norton) greater than the previous version, while Billet and Schultes characterized a large number of packings both random and structured type in different sizes/materials for distillation and absorption/desorption processes. The Billet and Schultes model thanks to a large number of experiments and used packings, which makes the strength of this correlation, turns out to be quite reliable with average errors of 8.3% for the liquid-side and 12.4% for the gas-side coefficient, providing fairly easy formulations that require only the use of two fitting parameters for the coefficients (ky and kx). It should be noted that when used for structured packings only the void fraction and nominal surface area of the packing data are needed, unlike the other correlations which require other characteristic dimensions of the packing. On the contrary, the SRP model requires the use of four fitting parameters, one of which for the interfacial area. Generally, the model equations proposed for ae calculation are not calibrated through the use of fitting parameters because the interfacial area is difficult to measure experimentally and in fact a calibration procedure on the coefficients kxae and kyae is preferred, introducing fitting parameters in the equations for the gas side (ky) and liquid side (kx). However, despite the Authors' efforts to revise the previous version, this model provides an error of about ±24% considering the experimentally measured HETP values. Furthermore, among the other correlations examined, the SRP model couples a predictive model for pressure drops in the mass transfer model to calculate the variation in liquid hold-up and film thickness with an iterative algorithm. This complication makes this correlation more complex in use but on the other hand allows to estimate pressure drops and mass transfer coefficients simultaneously.
The new generation correlations proposed by Brunazzi and Paglianti [13] and Olujić et al. [14] or Delft model are very accurate and complex formulations compared to the previous models but are valid only for specific types of structured packing and applications. Brunazzi and Paglianti tested Mellapak Y series and BX structured packing by Sulzer in plastic and metal material for absorption and desorption applications while Olujić characterized the Montz metal packing class by Koch-Glitsch in different types (nominal areas and corrugation angles) for distillation applications also for column pressure higher than 1 atm. The use of different theoretical approaches compared to two-films and penetration theories make these correlations more complex to use beacause several physical, geometric and fluid dynamic parameters have to be calculated. The Delft model requires the use of three fitting parameters and provides errors of approximately ±12% with respect to the experimentally calculated HETP values. While the Brunazzi and Paglianti model requires the use of four fitting parameters, of which three only for the liquid-side coefficient, furthermore the correlation for kx is based on an iterative algorithm on the height of the packing column which significantly increases the computational efforts required. Despite this the errors found with respect to the experiments are ±15% for the liquid-side and ±19% for the gas-side coefficient.
Among the new generation correlations, the model of Hanley and Chen [15] is probably the most reliable one since it is based on a set of equations containing dimensionless groups, fitting parameters and functional dependencies obtained with data fitting procedure from Bravo and Billet and Schultes experiments. This correlation based on a large number of experimental data has the benefit of being valid for distillation and absorption/desorption applications in different operating conditions and for both random and structured packing types (corrugated and gauze types) with errors of ±10% from experimentally calculated HETPs by Billet and Schultes and Bravo. Although this model appears to be the most accurate, on the other hand a large number of fitting parameters are required (ten for random packing and eleven/twelve for structured packing). It is also worth noting, that with respect to the two previous models, Hanley and Chen provide a dedicated calibration formulation for the interfacial area as in the SRP model, but using seven fitting parameters.
Despite the efforts made up to the last decade by the Authors to improve the correlations examined in this work, further refinements are required to achieve a definitive model equations able to overcome the problems related to the liquid distribution in packed towers, which plays a key role in the mass-transfer phenomena by modifying the mass-transfer coefficients and the interfacial packing area. To this end a better description of the fluid-dynamics and mass transfer behavior in multiphase flow processes is needed through a correct estimation of some fluid-dynamics parameters (i.e. the liquid film thickness and hold-up, and the interfacial surface area) that are considered the most controversial and debated parameters in the Authors' vision.
4. Conclusions
This work reviewed a number of predictive models for mass-transfer coefficients and wet interfacial area for packed columns equipped with both random and structured packing. The paper describes the most recognized models reported in the scientific literature [6][10][11][13][14][15] and includes specific data on the geometric and model fitting parameters found by the Authors. The models are also scrutinized according to their range of validity and their accuracy in describing experimental data purposely selected by the Authors.
From the analysis of the pros and cons of the correlations examined, the Billet and Schultes model seems to be the most reliable one, thanks to its wide range of validity and applicability to a large number of packing/applications,and the low errors of estimation (equal to 8.3% for the liquid-side and 12.4% for the gas-side coefficient), despite the use of only two fitting parameters.
While unavoidably suffering for the geometric constraints posed by the specific packing considered in their studies and, at a lower extent, to the size of the test plant, the modelling efforts made available in the pertinent literature by a number of Authors had the undiscussed merit to have discovered the key physical variables and packing geometry characteristics which influence the mass transfer coefficients on both the gas and the liquid-side. The parameters that are definitely more controversial in the Authors’ visions are the liquid hold-up, the liquid film thickness and the interfacial surface area, that are strictly related, and the definition of a characteristic dimension of the packing (i.e. of an hydraulic diameter).
To overcome the problems related to the indirect estimation of film thickness, liquid hold-up and the interfacial surface area, new experimental findings and modeling approaches available in the last 20 years literaure allow to refine the proposed correlations measuring these parameters. Among them, probably, the most interesting results derive from the use of optical technologies, e.g. tomography [41][42][43][44]. Similarly, several researchers have performed computational fluid dynamic (CFD) studies to estimate the flow characteristics in packed columns in reference conditions [45][46][47][48][49].
These efforts testify how alive is the interest in estimating the mass transfer coefficients for packing towers, and its relevance as a fundamental tool both for process designer and for specialist developer of packing internals. In spite of the current efforts, the availability of a definitive model able to predict the mass transfer coefficients for a generic packing geometry is still far to come.
LThe entry ist of Symbols from 10.3390/chemengineering5030043
List of Symbols
a Proportionality coefficient for the liquid Sherwood number in the BP model, [-]
ae Wet effective surface area of packing, [m2·m-3]
an Nominal surface area of packing, [m2·m-3]
Ac Section of column, [m]
b Functional parameter for Graetz liquid number in the BP model, [-]
c Functional parameter for Kapitza liquid number in the BP model, [-]
CESRP Surface renewal factor of the packing in the SRP model, [-]
CEDelft Surface renewal factor of the packing in the Delft model, [-]
CGBP Gas proportionality factor in the BP model, [-]
CGBRF Gas proportionality factor in the BRF model, [-]
CGBS Gas-side specific constant in the BS model, [-]
CGDelft Gas-side proportionality coefficient for laminar flow case in the Delft model, [-]
CGHC Gas proportionality factor in the HC model, [-]
CGSRP Gas proportionality factor in the SRP model, [-]
CGOTO Gas proportionality model factor in the OTO model, [-]
CLBRF Liquid-side proportionality model factor in the BRF model, [-]
CLBS Liquid-side proportionality model factor in the BS model, [-]
CLDelft Liquid-side proportionality coefficient in the Delft model, [-]
CLHC Liquid-side proportionality model factor in the HC model, [-]
CLSRP Liquid-side proportionality model factor in the SRP model, [-]
CLOTO Liquid-side proportionality model factor in the OTO model, [-]
CmHC Correction factor related to construction material, [-]
d Characteristic dimension of the liquid film, [m]
D Column diameter, [m]
deq Equivalent diameter, [m]
DG Gas diffusivity in the gas phase, [m2·s-1]
dh Hydraulic diameter, [m]
dhG Hydraulic diameter of triangular gas flow channel, [m]
DL Gas diffusivity in the liquid phase, [m2·s-1]
dp Diameter of a sphere possessing the same surface are as a piece of packing, [m]
FG Gas load factor, [Pa0. 50.5]
FL Liquid load factor, [m/h]
FrL Froude liquid number, [-]
FSE Surface enhancement factor in the SRP model, [-]
Ft Correction factor for total hold-up due to effective wetted area in the SRP model, [-]
Fθ,G Gas-side mass transfer coefficient dependence on crimp inclination angle, [-]
Fθ,L Liquid-side mass transfer coefficient dependence on crimp inclination angle, [-]
g Acceleration of gravity, [m·s-2]
GrL Graetz liquid number, [-]
hL Volumetric liquid hold-up, [m-3·m-3]
KaL Kapitza liquid number, [-]
kx Liquid-side mass transfer coefficient per surface unit, [kmol·m-2·s-1]
kxae Liquid-side volumetric mass transfer coefficient per surface unit, [kmol·m-3·s-1]
ky Gas-side mass transfer coefficient per surface unit, [kmol·m-2·s-1]
kyae Gas-side volumetric mass transfer coefficient per surface unit, [kmol·m-3·s-1]
lG,pe Length of the triangular gas flow channel in a packing element, [m]
n Correction exponent for the effective area in Delft model, [-]
P Operating pressure, [atm]
ReG Reynolds gas number, [-]
ReGrv Reynolds gas number based on relative effective velocity between gas and liquid, [-]
ReL Reynolds liquid number, [-]
ScG Schmidt gas number, [-]
ScL Schmidt liquid number, [-]
Sp Slant height of a packing corrugation, [m]
T Operating temperature, [°CK]
te Exposure time, [s]
tG Gas contact time, [s]
tL Time necessary for renewal of interface area, [s]
uLe Liquid effective velocity through the packing channel, [m·s-1]
uLs Superficial liquid velocity, [m·s-1]
WeL Weber liquid number, [-]
Z Packing height, [m]
Greek Symbols
α Liquid-side mass transfer coefficient dependence on crimp inclination angle in the HC model, [-]
β Functional parameter for Reynolds gas number in the HC model, [-]
γ Gas-side mass transfer dependence on crimp inclination angle in the HC model, [-]
Γ Liquid flow per unit length of perimeter, [kg·m-1·s-1]
γc contact angle accounts for surface material wettability, [°]
δf Liquid film thickness, [m]
ΔP/Z Total pressure drops per meter of packing, [Pa·m-1]
ΔP/Zfloood Pressure drops per meter of packing at flooding condition, [Pa·m-1]
εp Void volumetric fraction of the packing, [m-3·m-3]
ζGL Interaction coefficient for gas-liquid friction losses in the Delft model, [-]
η Proportionality coefficient for the wet surface area in the HC model, [-]
θc Inclination or corrugation angle, [°]
θL Slope of the steepest descent line with respect to the horizontal axis, [°]
κ Functional parameter for Reynolds gas number in the HC model, [-]
λ Functional parameter for Reynolds liquid number in the HC model, [-]
μG Mass gas viscosity, [kg·m-1·s-1]
μL Mass liquid viscosity, [kg·m-1·s-1]
μLo Dynamic viscosity of water at 20 °C, [kg·m-1·s-1]
ν Functional parameter for Weber liquid number in the HC model, [-]
ρG Mass gas density, [kg·m3]
ρy Molar gas density, [kmol·m-3]
ρx Molar liquid density, [kmol·m-3]
ρL Mass liquid density, [kg·m-3]
σc Critical surface tension of packing material, [N·m-1]
σL Liquid surface tension, [N·m-1]
φ Fraction of the triangular flow channel occupied by liquid, [-]
χ Functional parameter for Froude liquid number in the HC model, [-]
ψ Wet surface area dependence parameter on the gas to liquid viscosity ratio in the HC model, [-]
ω Wet surface area dependence parameter on the gas to liquid density ratio in the HC model, [-]
Ωp Fraction of packing surface area occupied by holes, [m-3·m-3]
Abbreviations
BP Referred to the work of Brunazzi and Paglianti (1997)
BRF Referred to the work of Bravo et al. (1985)
BS Referred to the work of Billet and Schultes (1993)
Delft Referred to the work of Olujić et al. (2004)
HC Referred to the work of Hanley and Chen (2012)
OTO Referred to the work of Onda et al. (1968)
SRP Referred to the work of Bravo et al. (1992)
References
- Mac, J.K.; Salten, A.H.J.; Mac, J.F. A new hydrodynamic analogy model for the determination of transport phenomena in random packings. 2020, doi:10.1016/j.ces.2020.116246.
- Mackowiak, J.; Mackowiak, J.F. Random Packings. In Distillation: Equipment and Processes; Wielkopolski, Poland, 2014; pp. 85–144 ISBN 9780123868787.
- Große Daldrup, A.; Crine, M.; Marchot, P.; Toye, D.; Kenig, E.Y. An approach to separation efficiency modelling of structured packings based on X-ray tomography measurements: Application to aqueous viscous systems. Chem. Eng. Sci. 2019, 204, 310–319, doi:10.1016/j.ces.2019.03.059.
- Cornell, D.; Knapp, W.G.; Fair, J.R. Mass transfer efficiency packed columns: part 1. Chem. Eng. Pro 1960, 56, 68–74.
- McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering; McGraw-Hill, Ed.; 1993; ISBN 0070448442.
- Onda, K.; Takeuchi, H.; Okumoto, Y. Mass transfer coefficients between gas and liquid phases in packed columns. J. Chem. Eng. Japan 1968, 1, 56–62, doi:10.1252/jcej.1.56.
- Bolles, W.L.; Fair, J.R. Performance and design of packed distillation columns. Inst. Chem. Eng. Symp. Ser. 1979, 56, 35.
- Bravo, J.L.; Rocha, J.A.; Fair, J.R. Mass transfer in Gauze Packings. Hydrocarb. Process. 1985, 64, 91–95.
- Shi, M.; Mersmann, A. Effective Interfacial Area in Packed Columns. Ger. Chem. Eng. 1985, 8, 87–96.
- Bravo, J.L.; Rocha, J.A.; Fair, J.R. A comprehensive model for the performance of columns containing st ructured packings. Inst. Chem. Eng. Symp. Ser. 1992, 128, A489--A507.
- Billet, R.; Schultes, M. Predicting mass transfer in packed columns. Chem. Eng. Technol. 1993, 16, 1–9, doi:10.1002/ceat.270160102.
- Billet, R.; Schultes, M. Prediction of mass transfer columns with dumped and arranged packings: Updated summary of the calculation method of Billet and Schultes. Chem. Eng. Res. Des. 1999, 77, 498–504, doi:10.1205/026387699526520.
- Brunazzi, E.; Paglianti, A. Liquid-Film Mass-Transfer Coefficient in a Column Equipped with Structured Packings. Ind. Eng. Chem. Res. 1997, 36, 3792–3799, doi:10.1021/ie970045h.
- Olujić, Ž.; Behrens, M.; Colli, L.; Paglianti, A. Predicting the efficiency of corrugated sheet structured packings with large specific surface area. Chem. Biochem. Eng. Q. 2004, 18, 89–96.
- Hanley, B.; Chen, C.C. New mass-transfer correlations for packed towers. AIChE J. 2012, 58, 132–152, doi:10.1002/aic.12574.
- Chávez, R.H.; De Guadarrama, J.J.; Hernández-Guerrero, A. Effect of the structured packing on column diameter, pressure drop and height in a mass transfer unit. Int. J. Thermodyn. 2004, 7, 141–148, doi:10.5541/ijot.1034000135.
- Chavez, R.H.; De Guadarrama, J.J. Comparison of structured packings in CO2 absorber with chemical reactions. Chem. Eng. Trans. 2010, 21, 577–582, doi:10.3303/CET1021097.
- Ghaemi, A.; Hemmati, A. Mass transfer coefficient for PZ + CO2 + H2O system in a packed column. Heat Mass Transf. und Stoffuebertragung 2020, doi:10.1007/s00231-020-02955-1.
- Iliuta, I.; Petre, C.F.; Larachi, F. Hydrodynamic continuum model for two-phase flow structured-packing- containing columns. Chem. Eng. Sci. 2004, 59, 879–888, doi:10.1016/j.ces.2003.11.020.
- Orlando, A.E.; Medina, L.C.; Mendes, M.F.; Nicolaiewsky, E.M.A. HETP evaluation of structured packing distillation column. Brazilian J. Chem. Eng. 2009, 26, 619–633, doi:10.1590/s0104-66322009000300017.
- Razi, N.; Svendsen, H.F.; Bolland, O. Assessment of mass transfer correlations in rate-based modeling of a large-scale CO2 capture with MEA. Int. J. Greenh. Gas Control 2014, 26, 93–108, doi:10.1016/j.ijggc.2014.04.019.
- Rocha, J.A.; Bravo, J.L.; Fair, J.R. Distillation columns containing structured packings: A comprehensive model for their performance. 2. Mass-transfer model. Ind. Eng. Chem. Res. 1996, 35, 1660–1667, doi:10.1021/ie940406i.
- Shetty, S.; Cerro, R.L. Fundamental Liquid Flow Correlations for the Computation of Design Parameters for Ordered Packings. Ind. Eng. Chem. Res. 1997, 36, 771–783, doi:10.1021/ie960627j.
- Song, D.; Seibert, A.F.; Rochelle, G.T. Effect of liquid viscosity on the liquid phase mass transfer coefficient of packing. Energy Procedia 2014, 63, 1268–1286, doi:10.1016/j.egypro.2014.11.136.
- Tsai, R.E. Mass Transfer Area of Structured Packing. PhD Thesis Univ. Texas Austin 2010.
- Tsai, R.E.; Seibert, A.F.; Eldridge, R.B.; Rochelle, G.T. A Dimensionless Model for Predicting the Mass-Transfer Area of Structured Packing. AIChE J. 2011, 57, 1173–1184, doi:10.1002/aic.
- Wang, C. Mass Transfer Coefficients and Effective Area of Packing. 2015.
- Chung, T.W.; Ghosh, T.K.; Hines, A.L. Comparison between Random and Structured Packings for Dehumidification of Air by Lithium Chloride Solutions in a Packed Column and Their Heat and Mass Transfer Correlations. Ind. Eng. Chem. Res. 1996, 35, 192–198, doi:10.1021/ie940652u.
- Wilson, I.D. Gas-Liquid Contact Area of Random and Structured Packing, University of Texas at Austin, 2004.
- Xu, Z.P.; Afacan, A.; Chuang, K.T. Predicting mass transfer in packed columns containing Structured Packings. 2000, 78.
- Zarei, M.M.; Zivdar, M.; Fazllolahi, F. High Capacity of Columns of Stabilizer Unit of Shiraz Refinery Using Structured Packing. 2013, 2, 83–87.
- Flagiello, D.; Di Natale, F.; Erto, A.; Lancia, A. Wet oxidation scrubbing (WOS) for flue-gas desulphurization using sodium chlorite seawater solutions. Fuel 2020, 277, 118055, doi:10.1016/j.fuel.2020.118055.
- Flagiello, D.; Erto, A.; Lancia, A.; Di Natale, F. Dataset of wet desulphurization scrubbing in a column packed with Mellapak 250.X. Data Br. 2020, 33, 106383, doi:10.1016/j.dib.2020.106383.
- Flagiello, D.; Di Natale, F.; Lancia, A.; Erto, A. Characterization of mass transfer coefficients and pressure drops for packed towers with Mellapak 250.X. Chem. Eng. Res. Des. 2020, 161, 340–356, doi:10.1016/j.cherd.2020.06.031.
- Flagiello, D.; Parisi, A.; Lancia, A.; Carotenuto, C.; Erto, A.; Di Natale, F. Seawater desulphurization scrubbing in spray and packed columns for a 4.35 MW marine diesel engine. Chem. Eng. Res. Des. 2019, 148, 56–67, doi:10.1016/j.cherd.2019.05.057.
- Flagiello, D.; Lancia, A.; Erto, A.; Natale, F. Di Desulphurization of combustion flue-gases by Wet Oxidation Scrubbing (WOS). Proc. 42th ASICI, Ravenna, Italy 2019, 5–10.
- Flagiello, D.; Di Natale, F.; Carotenuto, C.; Erto, A.; Lancia, A. Seawater desulphurization of simulated flue gas in spray and packed columns: An experimental and modelling comparison. Chem. Eng. Trans. 2018, 69, 799–804, doi:10.3303/CET1869134.
- Flagiello, D.; Erto, A.; Lancia, A.; Di Natale, F. Experimental and modelling analysis of seawater scrubbers for sulphur dioxide removal from flue-gas. Fuel 2018, 214, 254–263, doi:10.1016/j.fuel.2017.10.098.
- Flagiello, D.; Di Natale, F.; Carotenuto, C.; Erto, A.; Lancia, A. Marine diesel engine flue gas desulphurization by seawater scrubbing in a structured packing absorption column. Proc. 40th ASICI, Rome 2017, 69, 3–8.
- Flagiello, D.; Parisi, A.; Lancia, A.; Di Natale, F. A Review on Gas-Liquid Mass Transfer Coefficients in Packed-Bed Columns. ChemEngineering 2021, 5, 43.
- Doan, H.D.; Lohi, A. Measurement of Liquid Velocity and Liquid Distribution in a Packed Bed Using Electrical Resistance Tomography. 2007.
- Wehrli, M.; Kögl, T.; Linder, T.; Arlt, W. An Unobstructed View of Liquid Flow in Structured Packing. 2018, 69, 775–780, doi:10.3303/CET1869130.
- Wu, H.; Buschle, B.; Yang, Y.; Tan, C.; Dong, F.; Jia, J.; Lucquiaud, M. Liquid distribution and hold-up measurement in counter current fl ow packed column by electrical capacitance tomography. Chem. Eng. J. 2018, 353, 519–532, doi:10.1016/j.cej.2018.07.016.
- Green, C.W.; Farone, J.; Briley, J.K.; Eldridge, R.B.; Ketcham, R.A.; Nightingale, B. Novel application of X-ray computed tomography: Determination of gas/liquid contact area and liquid holdup in structured packing. Ind. Eng. Chem. Res. 2007, 46, 5734–5753, doi:10.1021/ie0701827.
- Haroun, Y.; Raynal, L. Use of Computational Fluid Dynamics for Absorption Packed Column Design. Oil Gas Sci. Technol. 2016, 71, doi:10.2516/ogst/2015027.
- Lassauce, A.; Alix, P.; Raynal, L.; Royon-Lebeaud, A.; Haroun, Y. Pertes de charge, Capacite´ et aires de transfert de matière requises pour le captage du co2en post-combustion par solvants. Oil Gas Sci. Technol. 2014, 69, 1021–1034, doi:10.2516/ogst/2013154.
- Haroun, Y.; Raynal, L.; Alix, P. Prediction of effective area and liquid hold-up in structured packings by CFD. Chem. Eng. Res. Des. 2014, 92, 2247–2254, doi:10.1016/j.cherd.2013.12.029.
- Macfarlan, L.H.; Seibert, A.F.; Phan, M.T.; Eldridge, R.B. CFD-based study on structured packing geometry. Chem. Eng. Sci. 2021, 243, 116767, doi:10.1016/j.ces.2021.116767.
- Salten, A.H.J.; Kenig, E.Y. Model based random packing optimisation for absorption processes using the hydrodynamic analogy concept. Chem. Eng. Sci. 2021, 242, 116670, doi:10.1016/j.ces.2021.116670.