Quantum chromodynamics (QCD) is the theory of strong interactions of quarks and gluons collectively called partons, the basic constituents of all nuclear matter. Its non-abelian character manifests in nature in the form of two remarkable properties: color confinement and asymptotic freedom. At high energies, perturbation theory can result in the growth and dominance of very gluon densities at small-x. If left uncontrolled, this growth can result in gluons eternally growing violating a number of mathematical bounds. The resolution to this problem lies by balancing gluon emissions by recombinating gluons at high energies : phenomena of gluon saturation. High energy nuclear and particle physics experiments have spent the past decades quantifying the structure of protons and nuclei in terms of their fundamental constituents confirming predicted extraordinary behavior of matter at extreme density and pressure conditions. In the process they have also measured seemingly unexpected phenomena. We will give a state of the art review of the underlying theoretical and experimental tools and measurements pertinent to gluon saturation physics. We will argue for the need of high energy electron-proton/ion colliders such as the proposed EIC (USA) and LHeC (Europe) to consolidate our knowledge of QCD in the small x kinematic domains.
- gluon saturation
- color glass condensate
- QCD
- electron ion colliders
- LHC
- LHeC
- EIC
- RHIC
1. Introduction
Quantum chromodynamics (QCD) is the theory of strong interactions of quarks and gluons collectively called partons, the basic constituents of all nuclear matter. Its non-abelian character manifests in nature in the form of two remarkable properties: color confinement and asymptotic freedom [1][2][3][1,2,3]. Confinement forbids the existence of quarks and gluons in free form or separated by long distances, allowing only colorless bound states such as mesons and baryons. Asymptotic freedom, on the other hand, states that at short distances, quarks and gluons interact weakly due to smallness of the coupling constant α s at asymptotically high energies. The latter property formed the theoretical basis behind the parton model [4][5][6][4,5,6], allowing the use of perturbation theory while leading to the successful description of a plethora of experimental results from fixed target experiments to high energy colliders. A multi-decade endeavor to quantify the structure of hadrons was launched with the introduction of the universal parton distribution functions (PDFs) which obey the DGLAP (Dokshitzer–Gribov–Lipatov–Altarelli–Parisi) renormalization group equation [7][8][9][10][7,8,9,10]. These PDFs describe the parton densities as functions of the longitudinal momentum fraction x . Beyond this one-dimensional picture, transverse momentum dependent (TMD) PDFs have been introduced to characterize the three-momenta of partons inside hadrons [11][12][13][11,12,13]. More recently, the complementary generalized parton distributions (GPDs) have been defined by furnishing PDFs with the two-dimensional transverse spatial distribution of partons resulting in a tomographic picture of hadrons and nuclei [14][15][16][14,15,16].
At high energies (or small x ), gluon densities grow quickly resulting in a large parton occupation number. This growth is expected to be controlled by nonlinear QCD effects at sufficiently small- x [17][18][17,18]. An appropriate description of the fundamental degrees of freedom of hadrons and nuclei in this regime is in terms of classical strong gluon fields, replacing the usual partonic description. A description of this high density regime is given by the Color Glass Condensate (CGC), a semi-classical effective field theory (EFT) for small- x gluons [19][20][21][22][23][19,20,21,22,23].
High-energy nuclear and particle physics experiments have spent the past decades quantifying the structure of protons and nuclei in terms of their fundamental constituents confirming extraordinary behaviour of matter at extreme density and pressure conditions. In the process they have also measured seemingly unexpected phenomena which will need a new generation of theoretical efforts as well as pertinent collider experiments. These last decades have also resulted on number of gluon saturation theoretical reviews which have paved the foundation for the current document [24][25][26][27][28][24,25,26,27,28].
This paper is organized as follows. Having given a brief introduction, we then proceed to Section 2 , which describes the principal underlying theoretical tools for the description of a gluon saturated state. Section 3 gives a selected overview of experimental signatures to date, while Section 4 discusses future facilities pertinent for the discovery and quantification of gluon saturation. Section 5 gives an outlook for our field followed by Acknowledgments to the people and institutions that made this manuscript possible.
2. Color Glass Condensate Effective Field Theory
This section will serve as a description to the underlying principles behind the Color Glass Condensate (CGC) as the effective field theory for saturated gluons. We will discuss the separation of degrees of freedom into sources and fields and the computation of observables in the CGC in Section 2.1 . Light-like Wilson lines and their correlators in the context of high-energy scattering will follow in Section 2.2 , which will include a discussion on the dipole correlator and the saturation scale. Section 2.3 will provide some examples of high energy processes in the CGC and discuss basic features of saturation. We briefly discuss the elements of small- x quantum evolution in Section 2.4 , where we introduce the Balitsky–Kovchegov equation and the JIMWLK evolution for the evolution of the sources. We note that a detailed exposition of the subject can be found in the reviews [24][25][24,25] as well as the text book in [26].
In the next section, we will see the manifestations of these correlators of light-like Wilson lines in concrete high energy processes in QCD.
As discussed in the previous section, high-energy scattering processes in the CGC are expressed in terms of correlators of light-like Wilson lines with impact factors that can be systematically computed in perturbation theory. In this section, we provide a few examples.
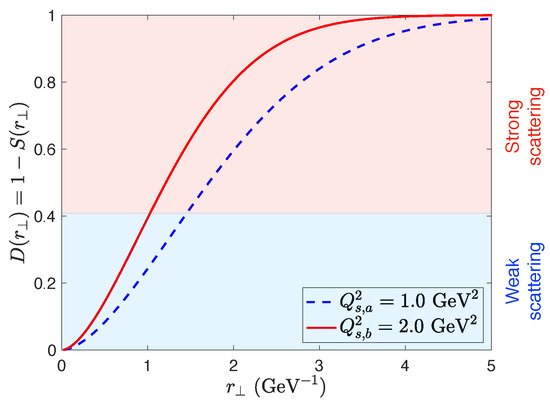
In order to access the saturated regime, one has to probe dipole sizes r ⊥ ∼ 1/ Q s (see Figure 13 ). The light-cone wave functions Ψ λ γ ∗ rapidly suppress dipoles with sizes r ⊥ 2≳ 1/ Q 2 (more precisely r ⊥ 2≳ 1/ z ( 1− z ) Q 2). These two observations imply that saturation effects in DIS at small- x are more visible at lower values of photon virtuality Λ Q C D 2≪ Q 2≲ Q s 2. At high virtualities, one probes the weak scattering regime where gluon saturation has not yet set in.
3. Experimental Signatures to Date
Diffractive observables are characterized by a rapidity gap (the absence of particles produced in a given rapidity window) which originates from a color neutral exchange between the two colliding systems. As gluons carry color, this exchange requires at least two gluons which must be in the color singlet state. Consequently, diffractive measurements are sensitive to the “square” of the the gluon distribution (at lowest order in perturbation theory). Compared to inclusive measurements, this enhanced sensitivity to the gluon distribution makes diffractive observables excellent candidates for gluon saturation searches at small- x . In this section, we will mostly focus on diffractive production in the collision of a photon (virtual or real) with a proton or nucleus. This can be realized in deep inelastic scattering (DIS) and ultra-peripheral collisions (UPCs).
As previously noted, the free parameters in the dipole models are typically chosen to reproduce HERA data, models are then used for predictions at RHIC and the LHC. However, saturation effects at HERA might be weak, as we argued in our discussion of the structure functions. The authors of [63] find a similar description of HERA data when comparing fits with IPsat and IPnonsat, signaling that gluon saturation effects are weak, thus arguing for the need of nuclear DIS.
Semi-inclusive measurements defined where one or more particles are tagged, provide more detailed information about the dynamics of gluons than fully inclusive measurements such as structure functions. Experimental signatures of gluon saturation are expected to be imprinted in the transverse momentum and rapidity distributions of particles produced in hadronic collisions [103].
As discussed above, a common challenge to uncover gluon saturation in these observables is to assess the impact of Sudakov re-summation. Sudakov double logarithms can appear in these processes as a result of the incomplete cancellation between real and virtual contributions [153][167][153,167] and are enhanced when the transverse momentum of the produced particles/jets is large. As a consequence, the searches for saturation are restricted to low to moderate transverse momentum phase space, where the Sudakov does not overwhelm the effects of gluon saturation but where jet reconstruction or effects of hadronization might obscure signals of saturation.
4. A New Generation of High Energy DIS Colliders
The experimental discovery of gluon saturation will require comprehensive analyses at future colliders. By the same token quantifying its characteristics will need an in-depth energy, Q 2 and mass number dependence scan on a number of quantities. Critical measurements that can help us in the discovery of a gluon saturated state can be classified once again into three main groups: structure functions, exclusive reactions, and semi-inclusive reactions. Below we will discuss the expected manifestations of gluon saturation for each of these processes while keeping an open tab to other mechanisms that could shroud its attributes.
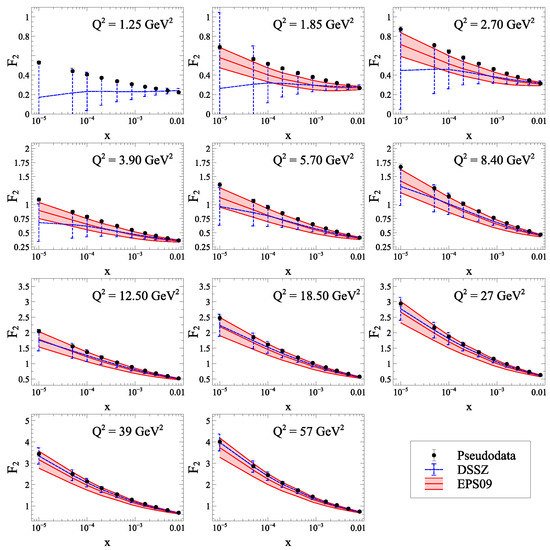
To more explicitly analyze the impacts of gluon saturation on the structure functions at the EIC, the authors of [191] generated pseudodata for electron–gold collisions, using the running-coupling Balitsky–Kovchegov evolution equation, and found tension between the compatibility of these saturated pseudodata with extrapolations of the existing nuclear PDFs (see Figure 2 7 ). While this tension might result in a signature of gluon saturation, it remains possible that refittings of nPDFs could accommodate for these differences as nPDFs are not well constrained in the low x regime. We have confidence that the high statistics of the EIC combined with forthcoming precise theoretical computations will distinguish both scenarios.
Incoherent production is also interesting as one expects sensitivity to subnucleonic fluctuations of various kinds. At the EIC, in addition to incoherent events in heavy nucleus DIS, we will also be able to study DIS off light-nuclei and study the interplay of short range correlations and gluon saturation [194][195][196][194,195,196].
We begin by discussing forward dihadron azimuthal correlations in ep, eA collisions. Motivated by the studies in pp and dAu collisions at RHIC and the LHC (c.f. Section 3.3.3 ), this process has received considerable attention in recent years and it is considered a promising channel for gluon saturation searches at the EIC (see also in [197] for photon–hadron azimuthal correlations).
