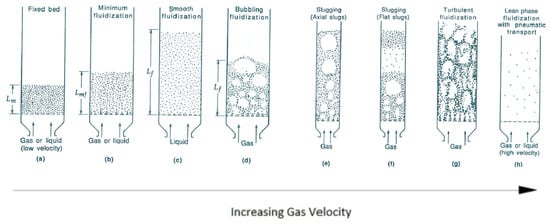
In the fluidized bed system, the performance of the reactor is affected by the hydrodynamic behaviors of the reactor in that fluid dynamics affects both heat and mass transfer.
- solid–fluid reaction
- reaction modelling
- single particle reaction
- fixed-bed reaction
- fluidized-bed reaction
1. Introduction
Different modelling methods have been developed to solve the reaction rate over the last few decades, from simplified models to complex CFD models. The simplest model is the shrinking particle model or shrinking core model for nonporous particles. More complex models include the random pore model, which accounts for the particle pore structure and the diffusion and reaction inside the pores.
While CFD simulation can provide detailed information on fluid dynamics and heat transfer in the solid/liquid reaction process, it is complex to build, requiring considerable computational resource and time. Therefore, for engineers who need a quick design of new product or process, or to perform a quick feasibility study or to evaluate or optimize the existing processes or operations within a limited time frame, CFD simulation could be too time-consuming to afford. In these cases, a quick modelling solution with appropriate correlations and empirical equations based on single particle reaction models becomes a desirable option.
2. Single Particle Reaction Models
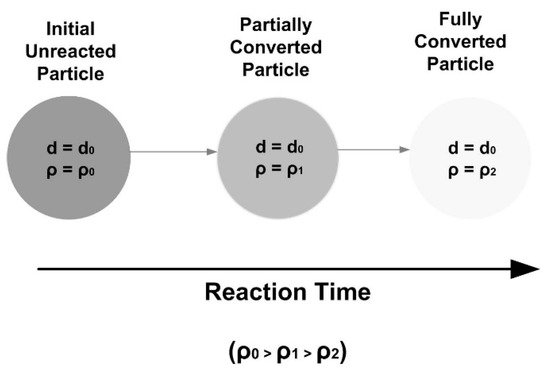
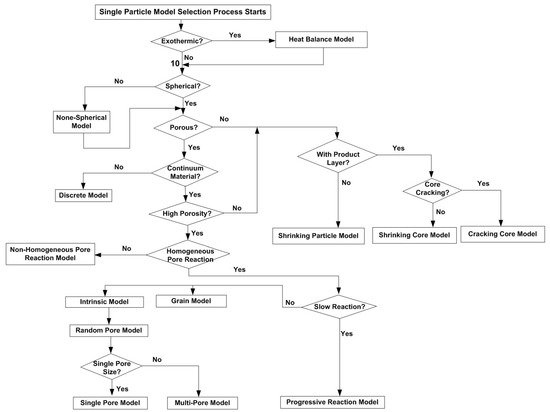
3. Reaction Models for Bed of Particles
3. Reaction Models for Bed of Particles
References
- Iwaszenko, S.; Howaniec, N.; Smolinski, A. Determination of random core model parameters for underground coal gasification simulation. Energy 2019, 166, 972–978.
- Salmi, T.; Grenman, H.; Warna, J.; Murzin, D.Y. Revisiting Shrinking Particle and Product Layer Models for Fluid-Solid Reactions―From Ideal Surfaces to Real Surfaces. Chem. Eng. Process. Process. Intensif. 2011, 50, 1076–1084.
- Bhatia, S.K. The effect of pore structure on the kinetics of fluid-solid reactions. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 1981.
- Gonzalez, J.A. Coupled fluid-solid thermal interaction modelling for efficient transient simulation of biphasic water-steam energy systems. Appl. Math. Model. 2020, 79, 566–593.
- Son, H.Y.; Roy, S. Fluid-solid reaction kinetics for solids of non-basic geometries: Application of the law of additive times in combination with the shape-factor methods. Metall. Mater. Trans. B 2020, 51, 601–610.
- Wen, C.Y. Noncatalytic heterogeneous solid–fluid reaction models. Ind. Eng. Chem. 1968, 60, 34–54.
- Martins, J.P.; Margarido, F. The cracking and shrinking model for solid–fluid reactions. Mater. Chem. Phys. 1996, 44, 156–169.
- Park, J.Y.; Levenspiel, O. The cracking core model for the reaction of solid particles. Chem. Eng. Sci. 1975, 30, 1207–1214.
- Gago, P.A.; Raeini, A.Q.; King, P. A spatially resolved fluid-solid interaction model for dense granular packs/soft-sand. Adv. Water Resour. 2020, 136, 103454.
- Ngo, S.I.; Lim, Y.I.; Lee, D.; Go, K.S.; Seo, M.W. Flow behaviours, reaction kinetics, and optimal design of fixed- and fluidized-beds for CO2 methanation. Fuel 2020, 275, 117886.
- Zhou, Z.; Yan, D.; Zhu, J.; Zheng, Y.; Li, H.; Zhu, Q. Simulation of the fluid-solid noncatalytic reaction based on the structure-based mass-transfer model: Shrinking core reaction. Ind. Eng. Chem. Res. 2020, 59, 17729–17739.
- Ishid, M.; Wen, C.Y. Comparison of kinetic and diffusional models for solid-gas reactions. AIChE J. 1968, 14, 311–317.
- Alexiadis, A.; Mazzarino, I. Design guidelines for fixed-bed photocatalytic reactors. Chem. Eng. Process. Process. Intensif. 2005, 44, 453–459.
- Alexiadis, A.; Baldi, G.; Mazzarino, I. Modelling of a photocatalytic reactor with a fixed bed of supported catalyst. Catal. Today 2001, 66, 467–474.
- Kunii, D.; Levenspiel, O. Fluidization Engineering; Butterworth-Heinemann: London, UK, 1991.
- Zhang, H.; Sun, Z.; Zhang, M.; Shao, Y.; Zhu, J. Comparison of the flow structure and regime transitions between a cylindrical fluidized bed and a square fluidized bed. Powder Technol. 2020, 376, 50–516.
- Alexiadis, A.; Gardin, P.; Domgin, J.F. Spot turbulence, breakup, and coalescence of bubbles released from a porous plug injector into a gas-stirred ladle. Metall. Mater. Trans. B 2004, 35, 949–956.
- Alexiadis, A.; Gardin, P.; Domgin, J.F. Probabilistic approach for break-up and coalescence in bubbly-flow and coupling with CFD codes. Appl. Math. Model. 2007, 31, 2051–2061.
