After the discovery of circular formations of single walled carbon nanotubes called fullerene crop circles, their structure has become one of the most researched amongst carbon nanostructures due to their particular interesting physical properties. Several experiments and simulations have been conducted to understand these intriguing objects, including their formation and their hidden characteristics. It is scientifically conceivable that these crop circles, nowadays referred to as carbon nanotori, can be formed by experimentally bending carbon nanotubes into ring shaped structures or by connecting several sections of carbon nanotubes. Toroidal carbon nanotubes are likely to have many applications, especially in electricity and magnetism. In this review, geometry, construction, modelling and possible applications are discussed and the existing known analytical expressions, as obtained from the Lennard-Jones potential and the continuum approximation, for their interaction energies with other nanostructures are summarised.
- carbonnanotori
- nanotechnology
- interactionenergy
- Lennard-Jonespotential
- continuum approximation
1. Introduction
Following their discovery [1], carbon nanostructures have become the subject of much interest from the scientific community in numerous diverse areas of application. They have many unique physical properties which are superior to other existing materials, such as their high electrical and thermal conductivities, high flexibility, and great tensile strength [2]. They have become one of the major materials driving technological developments with potential applications in many different areas, such as electrical devices from graphenes [3], genes carriers from fullerenes [4], gigahertz oscillators from carbon nanotubes [5] and gas absorbers from carbon nanocones [6].
One specific form of carbon nanostructures is carbon nanotori, which are doughnut-like structures. The seamless toroidal nanotubes having diameters ranging from 300 to 500 nm and rope diameters over 5–15 nm were first found while examining single-walled carbon nanotubes by scanning force and transmission electron microscopy [7]. Later, they were formed from a variety of different experimental methods including laser growth [7], organic reactions [8], chemical vapor deposition [9] and depositing hydrocarbon films in tokamak T-10 [10]. In addition, they can be theoretically constructed from a model that connects together several smaller carbon nanotube segments, perhaps involving different bend angles in order to complete the closed ring of the carbon nanotori [11,12,13,14]. Nanotori structures provide many novel properties, particularly in electronic and magnetic applications [15,16], and their properties are strongly dependent on their geometric parameters, temperature and the chiral vector of the carbon nanotubes used in their construction [16]. Because of their geometric structure, they can be used to trap or encapsulate other nanostructures either within the interior of the nanotori itself or within the central cavity. Since carbon nanotori and other nanostructures do not create bonds between molecules, their main interaction energy originates from the van der Waals interaction energy. By utilising classical applied mechanics, such interactions can be modelled with the Lennard-Jones potential [17]. Moreover, their interaction energy can often be analytically expressed in terms of special functions using the continuum approximation, which assumes that all atoms are uniformly distributed over the molecules so that summations from each atomic pair can be approximated by double surface integrations over the two molecules. Following this approach, the interaction energy of the carbon nanotori and other nanostructures, such as atoms, ions and fullerenes can be obtained as a function of the geometric parameters of the nanotori and the interacting nanostructures, and the distance between the two structures.
In the following two sections, construction techniques, physical characteristics and applications of carbon nanotori are reviewed. In Section 4, the concepts of continuum approximation and Lennard-Jones potential are introduced and in Section 5, the final energy formulae for a number of different systems related to the carbon nanotori are summarised. In Section 6, a brief overall summary is given.
2. Geometry and Construction of Carbon Nanotori
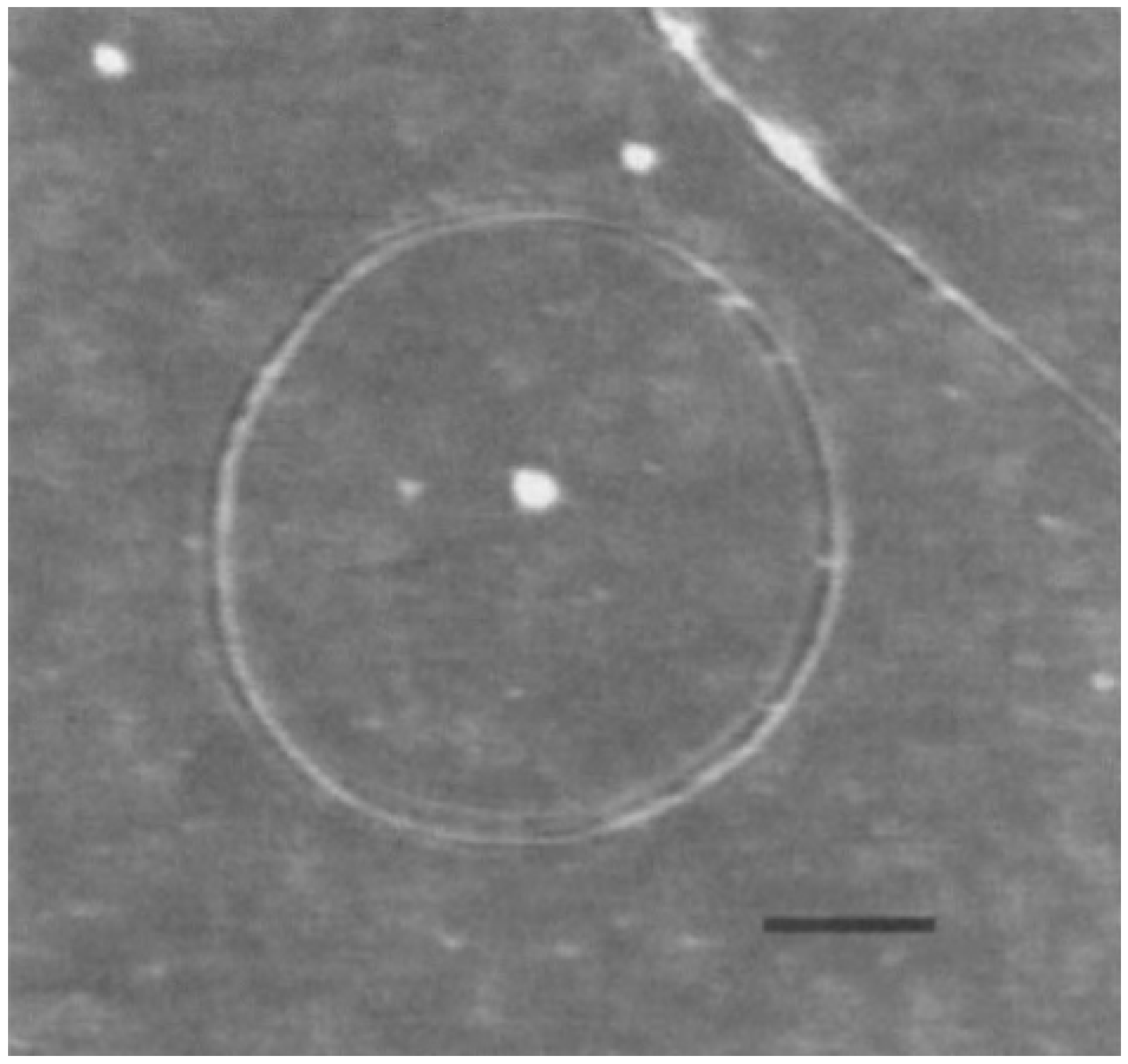
Carbon nanotori are the circular ring structures defined by two parameters describing their geometry, called major and minor radii. The major radius of the carbon nanotori is the radius or the distance between the centre to the centre of the curved tube, while the minor radius is the radius of the closed tube as illustrated in Figure 1. This experimentally determined figure is obtained from [18] and shows a toroidal structure of C750. The major radii are used to classify carbon nanotori into two groups. If their major radius is greater than 100 nm, they are regarded as large carbon nanotori, and otherwise, they are considered to be small carbon nanotori.
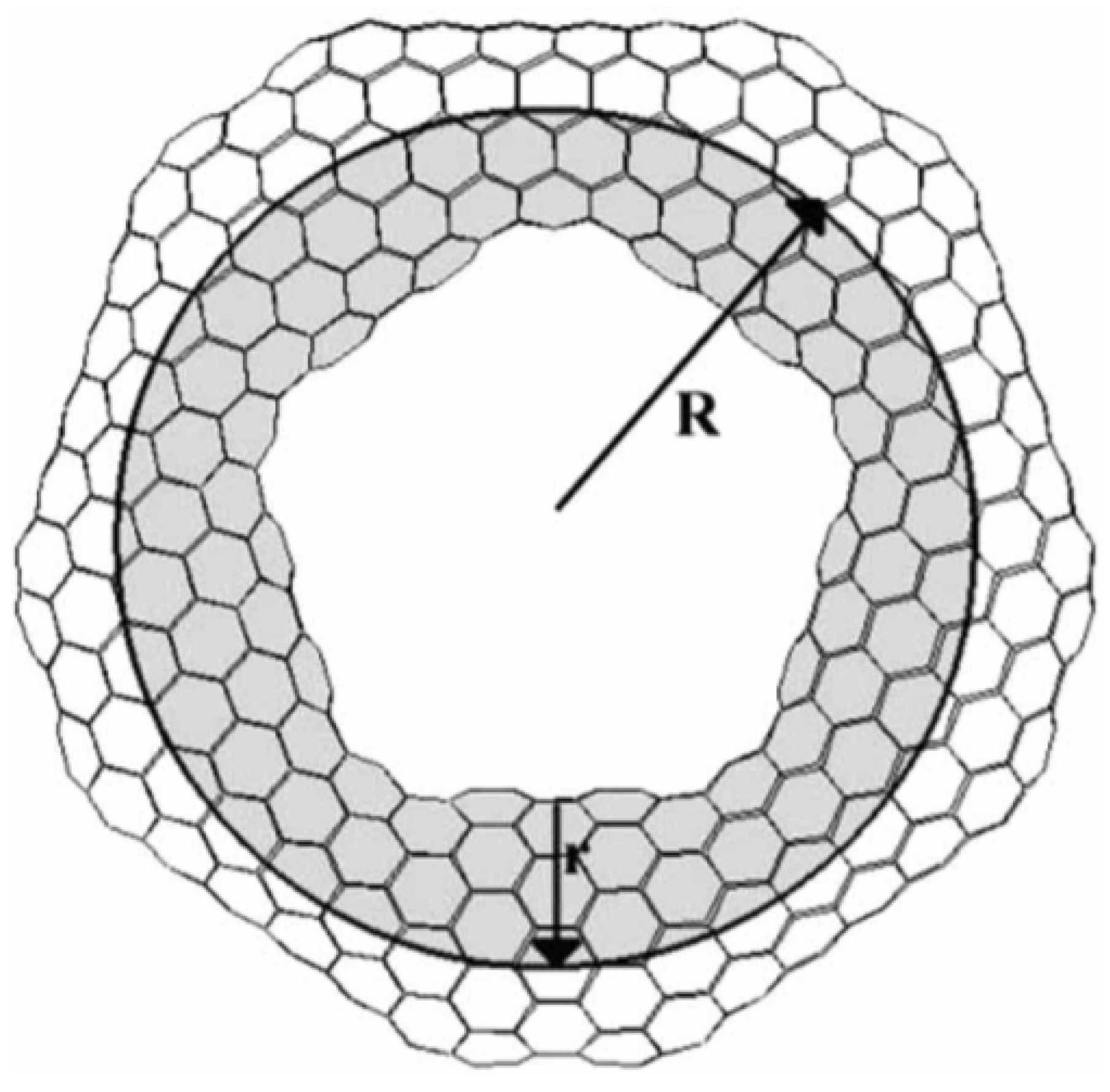
Figure 1.
R
r
However, smaller carbon nanotori and in particular those with major radii much smaller than 100 nm can at least theoretically be fabricated by introducing a pentagon-heptagon pair into the graphitic honeycomb networks of two carbon nanotubes [24,25]. The two carbon nanotubes need not be of the same type; for example one might be zigzag and the other tube armchair. In this method, the bend angle between two segments of the two different tubes is approximately 30∘, meaning that such 12 segments of carbon nanotubes are needed to construct a closed toroidal molecule. Experimentally, the bend angle is more likely to be 36∘ due to strain relaxation around the joints [26], and as a result, only 10 equal segments are required to complete a ring structure. In this event, the condition that each segment of carbon nanotubes be of the same length might be relaxed. In this way, a wide variety of carbon nanotori can be constructed by connecting segments of carbon nanotubes of different lengths, bend angles and types [27,28]. Figure 3 presents examples of such a construction.
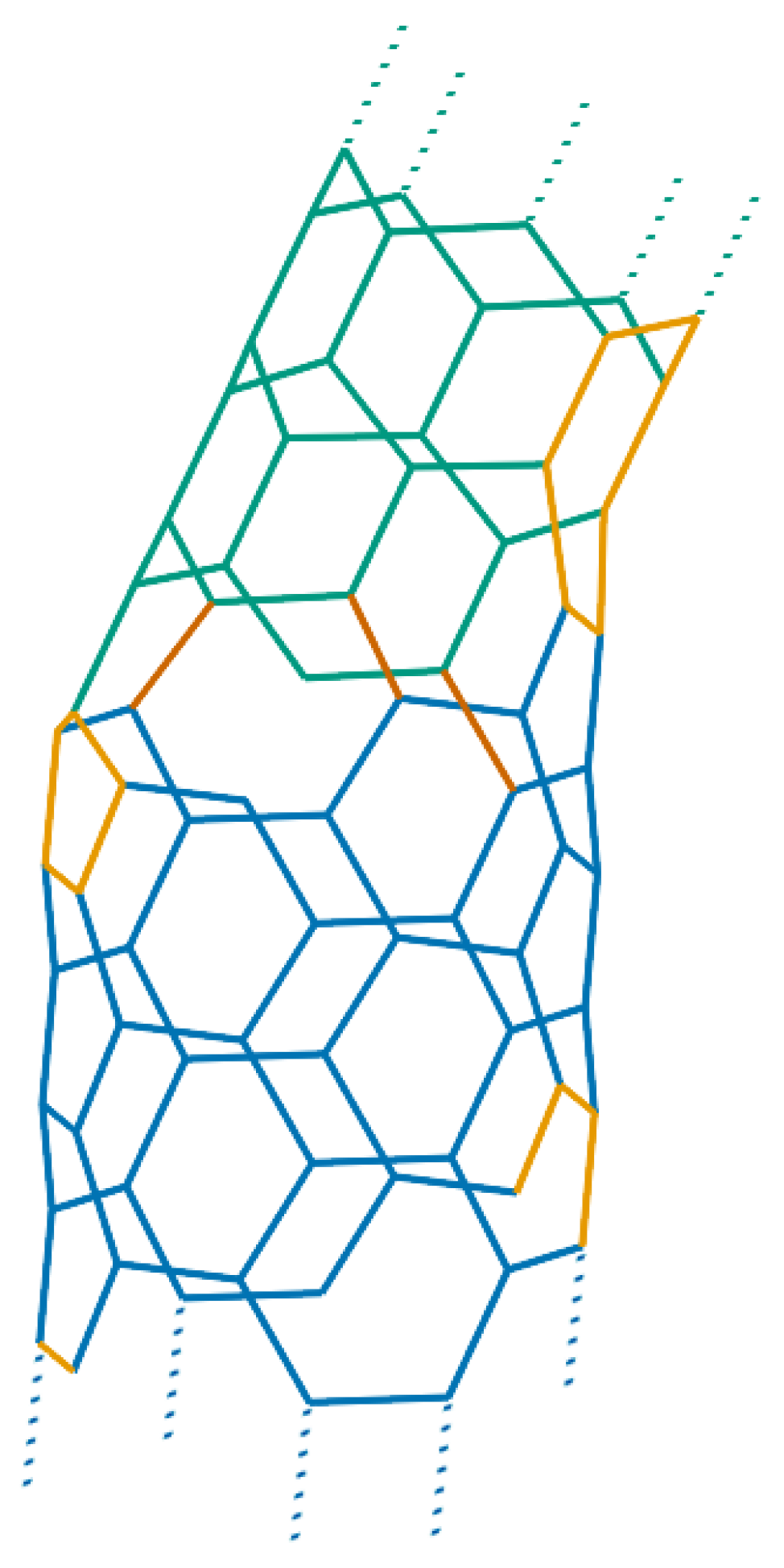
Carbon nanotori can also be produced by other modelling techniques, such as constructing from fullerenes using the Goldberg’s prescription [29,30], sewing the walls of single-walled [31,32,33], double-walled [34] or triple-walled [35] carbon nanotubes at both ends and fabricating from only pentagon and heptagon networks [36].
1. Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58.
2. Saito, R.; Dresselhaus, G.; Dresselhaus, M. Physical Properties of Carbon Nanotubes;World Scientific Publishing:Singapore, 1998.
3. Ray, S.C. Applications of Graphene and Graphene-Oxide Based Nanomaterials;William Andrew: Oxford, UK, 2015.
4. Bakry, R.; Vallant, R.; Haq, M.; Rainer, M.; Szabo, Z.; Huck, C.; Bonn, G. Medicinal applications of fullerenes. Int. J. Nanomed. 2007, 2, 639–649.
5. Thamwattana, N.; Hill, J.M. Nanotube bundle oscillators: Carbon and boron nitride nanostructures. Physica
B 2009, 404, 3906–3610.
6. Karousis, N.; Martinez, I.S.; Ewels, C.P.; Tagmatarchis, N. Structure, properties, functionalization, and
applications of carbon nanohorns. Chem. Rev. 2016, 116, 4850–4883.
7. Liu, J.; Dai, H.; Hafner, J.H.; Colbert, D.T.; Smalley, R.E. Fullerene ‘crop circles’. Nature 1997, 385, 780–781.
8. Geng, J.; Ko, Y.K.; Youn, S.C.; Kim, Y.H.; Kim, S.A.; Jung, D.H.; Jung, H.T. Synthesis of SWNT rings by
noncovalent hybridization of porphyrins and single-walled carbon nanotubes. J. Math. Chem. C 2008,
112, 12264–12271.
9. Zhou, Z.; Wan, D.; Bai, Y.; Dou, X.; Song, L.; Zhou, W.; Mo, Y.; Xie, S. Ring formation from the direct floating catalytic chemical vapor deposition. Physica E 2006, 33, 24–27.
10. Kukushkin, A.B.; Neverov, V.S.; Marusov, N.L.; Semenov, I.B.; Kolbasov, B.N.; Voloshinov, V.V.; Afanasiev, A.P.; Tarasov, A.S.; Stankevich, V.G.; Svechnikov, N.Y. Few-nanometer-wide carbon toroids in the
hydrocarbon films deposited in tokamak T-10. Chem. Phys. Lett. 2011, 506, 265–268.
11. Natsuki, T.; Tantrakarn, K.; Endo, M. Effects of carbon nanotube structures on mechanical properties. Appl. Phys. A 2004, 79, 117.
12. Zhang, X.F.; Zhang, Z. Polygonal spiral of coil-shaped carbon nanotubes. Phys. Rev. B 1995, 52, 5313–5317.
13. Dunlap, B.I. Constraints on small graphitic helices. Phys. Rev. B 1994, 50, 5134–8137.
14. Ihara, S.; Itoh, S. Helically coiled and toroidal cage forms of grapitic carbon. Carbon 1995, 33, 931–939.
15. Feng, C.; Liew, K.M. A molecular mechanics analysis of the buckling behavior of carbon nanorings under
tension. Carbon 2009, 47, 3508–3514. Appl. Sci. 2019, xx, 5 18 of 20
16. Liu, L.; Liu, F.; Zhao, J. Curved carbon nanotubes: From unique geometries to novel properties and peculiar applications. Nano Res. 2014, 7, 626–657.
17. Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035.
18. Yazgan, E.; Ta¸sci, E.; Malcio˘ glu, O.; Erkoç, S. Electronic properties of carbon nanotoroidal structures. J. Mol. Struc.-Theochem. 2004, 681, 231–234.
19. Ahlskog, M.; Seynaeve, E.; Vullers, R.J.M.; Haesendonck, C.V.; Fonseca, A.; Hernadi, K.; Nagy, J.B. Ring
formations from catalytically synthesized carbon nanotubes. Chem. Phys. Lett. 1999, 300, 202–206.
20. Martel, R.; Shea, H.R.; Avouris, P. Ring formation in single-wall carbon nanotubes. J. Phys. Chem. B 1999,103, 7551–7556.
21. Thess, A.R.; Lee, P.N.; Dai, H.; Petit, P.; Robert, J.; Xu, C.; Lee, Y.H.; Kim, S.G.; Rinzler, A.G.; Colbert, D.T.; et al. Crystalline ropes of metallic carbon nanotubes. Science 1996, 273, 483–487.
22. Meunier, V.; Lambin, P.; Lucas, A.A. Atomic and electronic structures of large and small carbon tori. Phys.
Rev. B 1998, 57, 14886.
23. Chang, I.L.; Chou, J.W. A molecular analysis of carbon nanotori formation. J. Appl. Phys. 2012, 112, 063523.
24. Dunlap, B.I. Connecting carbon tubules. Phys. Rev. B 1992, 46, 1933–1936.
25. Dunlap, B.I. Relating carbon tubules. Phys. Rev. B 1994, 49, 5643–5650.
26. Fonseca, A.; Hernadi, K.; Nagy, J.; Lambin, P.; Lucas, A.A. Model structure of perfectly grapitizable coiled
carbon nanotubes. Carbon 1995, 33, 1759–1775.
27. Cox, B.J.; Hill, J.M. New carbon molecules in the form of elbow-connected nanotori. J. Phys. Chem. C 2007,111, 10855–10860.
28. Baowan, D.; Cox, B.J.; Hill, J.M. Toroidal molecules formed from three distinct carbon nanotubes. J. Math.
Chem. 2008, 44, 515–527.
29. Ihara, S.; Itoh, S. Toroidal forms of graphitic carbon. Phys. Rev. B 1993, 47, 12908–12911.
30. Itoh, S.; Ihara, S. Toroidal forms of graphitic carbon. II. Elogated tori. Phys. Rev. B 1994, 48, 8323–8328.
31. Sano, M.; Kamino, A.; Okamura, J.; Shinkai, S. Ring closure of carbon nanotubes. Science 2001, 293, 1299–1301.
32. Guo, A.; Fu, Y.; Guan, L.; Zhang, Z.;Wu,W.; Chen, J.; Shi, Z.; Gu, Z.; Huang, R.; Zhang, X. Spontaneously formed closed rings of single-wall carbon nanotube bundles and their physical mechanism. J. Phys. Chem. C 2007, 111, 3555–3559.
33. Komatsu, N.; Shimawaki, T.; Aonuma, S.; Kimura, T. Ultrasonic isolation of toroidal aggregates of
single-walled carbon nanotubes. Carbon 2006, 44, 2091–2093.
34. Colomer, J.F.; Henrard, L.; Flahaut, E.; Tendeloo, G.V.; Lucas, A.A.; Lambin, P. Rings of double-walled carbon nanotube bundles. Nano Lett. 2003, 3, 685–689.
35. Yu, H.; Zhang, Q.; Luo, G.;Wei, F. Rings of triple-walled carbon nanotube bundles. Appl. PhysLett. 2006,
89, 223106.
36. László, I.; Rassat, A. Toroidal and spherical fullerene-like molecules with only pentagonal and heptagonal
faces. Int. J. Quantum Chem. 2001, 84, 136–139.
