1. Introduction

The unique control offered by single quantum systems, such as atoms or ions, has enabled an immense boost in the development of quantum technologies. Extending these technologies to larger masses is important both for fundamental questions on the nature of quantum physics at larger scales, and for the development of innovative devices such as ultra-high precision force sensors and accelerometers [1].

Electro-, magneto- or opto- mechanically controlled levitating objects in vacuum are fascinating in this regard and have been at the focus of intense recent research activity [2]. This attention is supported by the exquisite control that one can exert over the levitated objects. These platforms indeed allow addressing of numerous degrees of freedom, easy tuning of the trapping potential, as well as enabling free-fall experiments [3], as in atomic physics.

The promises of this schemes have been supported by recent experiments that reported trapped particles cooled to the quantum regime ^[4][5][6][7][7,8,9,10]. Towards this goal, amongst all condensed matter system, the negatively charged nitrogen-vacancy center (NV− center for short) in diamond centers stands out because of the ease with which one can optically polarize and read-out its electronic spin under ambient conditions. Most of the proposals initially designed for clamped oscillators coupled with NV− centers ^[8][9][10][14,16,17] can then be carried over to trapped diamonds ^[11][18] which are, in all current experiments, operating close to room temperature. Ensembles of NV− centers coupled identically to mechanical oscillators can also exhibit magnetic phase transitions, paving the way towards nano-scale magnetism with long-lived and controllable spins in a trapped particle ^[12][13][19,20].

This growing research field will drive advances in quantum metrology via quantum enhanced gyroscopy and matter-wave interferometry ^[12][14][15][19,21,22]. The spin–mechanical coupling also brings important advantages for quantum sensing and metrology by providing enhanced measurement sensitivity. At the single spin level it also features additional non-linearity and/or control that could be helpful to build non classical states of motion ^[11][18]. Finally, they could also serve as transducers between optical and RF signals via the mechanical mode ^[16][23].

In this review, we describe the state-of-the-art levitation systems that involve NV− centers and describe their specificities and limitations. The goal is not to draw a comparison between the performance of existing systems. Instead, we focus on the important results that have been accomplished and the remaining hurdles on the way towards operating in the quantum regime with these platforms.

In Section 2, we briefly present the existing levitation platform and the equations of motion describing the different mechanical modes. The Hamiltonian of the total coupled spin–mechanical system is derived in Section 4. Section 5 reviews experiments that demonstrate read-out of the mechanical motion of levitated particles using the NV spin. Finally, Section 8 presents the current challenges in spin-mechanics with trapped particles.

2. Sensing the Motion of a Trapped Particle Using NV

As we just described, the ESR frequencies depend strongly on the angle of the homogeneous magnetic field with respect to the NV axis, and on the center of mass in a magnetic field gradient. In the presence of a microwave drive on the diamond, the change in the photoluminescence from the NV− centers can then be used as a marker of the center of mass motion of diamonds or distant ferromagnetic particles, as pioneered in experiments with tethered oscillators ^[9][10][16,17]. With trapped diamond particles, the angular dependence of the NV center energy levels also means that it is possible to detect their full rotation and even their librational motion.

Figure 1a shows an ODMR obtained from optically trapped diamonds in water featuring broad lines due to significant angular Brownian motion in the presence of a magnetic field ^[17][84]. Similar ODMR shapes were observed in ^[18][19][54,63]. These results show that NV centers are an efficient tool to measure the rotation of particles. Further, the fully rotating regime may also shed new light on geometric phases acquired by NV centers as well as offering perspectives for efficient sensing of magnetic fields in the rotating frame ^[20][85].

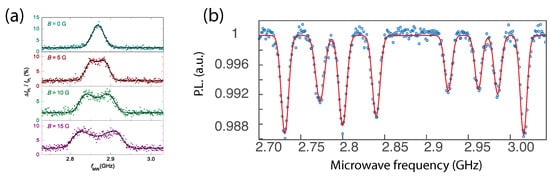
In ^[18][21][54,86], ODMR from diamond particles in Paul traps was also reported on angularly stable micro-diamonds (with typical librational frequencies in the kHz range). Eight ODMR lines were observed due to the four projections of the magnetic field onto the four possible NV axes in the diamond cristalline structure and thanks to the efficient particle angular confinement. Assuming thermalization with a gas at a temperature close to T = 300 K, the angular standard deviation is Δθ≈ 1 mrad (see Section 2). This value is smaller than the width given by the dipolar coupling between the NV and P1 centers (see Section 3).

Two recent experiments have even shown read out of the harmonic motion of a trapped particle using NV centers ^[22][23][35,70]. In the first experiment ^[23][70], a hybrid diamond-nickel particle was levitated in a Paul trap. The NV− centers in the diamond were employed to read-out the librational motion. In the second experiment ^[22][35], a magnet was levitating on top of superconducting sheet and a diamond containing a single NV− center was brought in the vicinity of the magnet to read-out its center of mass motion.

In order for NV centers to efficiently detect the center of mass motion, Gieseler et al. used broadband magnetic noise to excite the motion of the trapped micro-magnet (diameter ≈15μm). The magnetic field thermal noise at the NV location, generated by the 100 μm distant driven trapped magnet, was then observed in the power spectral density (PSD) of the NV PL evolution. Thanks to the high quality factor of the oscillator (Q≈106), tuning a microwave to the blue side of the ODMR signal, as shown in the top of Figure 2a, resulted in a sharp peak at the mechanical oscillator frequency.

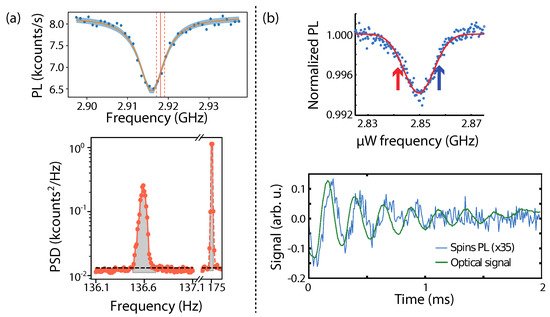
^[23][70] reported NV-based detection of the motion of a 10 μm hybrid ferromagnet/diamond particle. The latter was levitated in a Paul trap and the libration was detected in the time domain after parametric excitation of the magnetically confined librational mode. Figure 3b shows the ODMR (top trace) and the ring down of the librational mode (below) detected both using scattered light and the NV PL. Notably, the PL change was delayed with respect to the instantaneous particle motion due to a time lag between the motion and the magnetization.

These studies open a path towards the NV read-out of the Brownian motion of trapped harmonic oscillators. To reach this limit, more involved dynamical decoupling (DDC) techniques ^[10][17] could be used, with perspectives for attaining the zero-point motion sensitivity of the oscillator. Rabi oscillations, Ramsey and spin echoes from NV centers in a trapped diamond have in fact been observed already without significant deterioration of the T2 from either the charge noise or the angular Brownian motion ^[21][86]. Rabi oscillations were also observed in ^[24][53] using an optically trapped nanodiamond under weak magnetic fields.

3. Magnetic Forces and Torques on a Trapped Particle from the Spin of NV

We have discussed experiments where the trapped particle motion was read-out by NV spin states. In order to strongly couple a mechanical oscillator to spins, however, not only should the mechanical motion affect the spin state, but the spin should also alter the motion.

In this section, we review work on the reverse process where NV centers act on the motion. We start by a discussion on optimum sensing of the force and the torque induced by NV centers.

Presently, direct optical read-out of the motion of trapped particles using scattered light is more efficient than using embedded NV centers. Most experiments that use optical read-out are currently in the regime where the influence of collisions with the background gas dominates. Note that the ultimate sensitivity should be given by the quantum back-action of the measurement under low vacuum. This limited was recently reached in experiments with trapped nano-spheres

The most sensitive way to detect an external torque, with current technology, is to use optical interferometric detection and to modulate the torque at the mechanical frequency of the oscillator. Modulation of the amplitude of the NV induced spin-torque can be done straightforwardly by modulating the microwave tone that excites them. The minimum torque τsmin that can be detected in a time δT is then obtained by balancing the resulting signal amplitude and the standard deviation of the Brownian motion noise. (14)τsminδT=4kTγθI=4kTKtQωθ, where Q=ωθ/γθ is the quality factor of the mechanical oscillator libration, and Kt is the trap rigidity, namely Iωθ2.

Tethered torque sensors with sensitivities in the 10−23 N·m The largest sensitivities with levitating systems have been achieved using levitating silica nanospheres that are attached to form a dumbbell ^[25][91]. Trapped cristalline particles currently feature a lower torque sensitivity than trapped amorphous particles, partly because of their currently lower quality factor. /Hz was attained in ^[23][70] using soft ferromagnetic particles at room temperature and at pressure levels in the 10−2 mbar range, very close to the state-of-the-art torque sensing obtained at dilution fridge temperatures ^[26][90].

A similar formula can be obtained for the smallest detectable force acting on the center of mass mode, by replacing Q with ωz/γz, Kt by mωz2 and I by m. Sensitivities in the zeptonewton/Hz range were reported experimentally ^[27][28][29][28,92,93]. Amongst all spin–mechanical systems, trapped magnets currently feature record sensitivities in the 10−18 N/Hz range ^[22][30][35,44]. Note that at the low pressure levels employed in these experiments (≈10−5 mbar), damping is not determined by collisions with the background gas so the above model may not apply directly.

These last achievements not only show the capabilities of levitating systems, close to the sensing capabilities of MEMS, but also offer immediate perspectives for entering the quantum regime by coupling magnets to distant NV centers.

In this section, we discuss the parameters required for observing spin-dependent forces and torques on a trapped particle. We focus on the expected static shifts, assuming that the NV− centers have a lifetime that is greater than the typical time required to shift the angle or the center of mass. The latter is typically on the order of the period of the potential.

Using Equation (10), one finds that the torque applied to the diamond in the magnetic state |−1′⟩ reads (15)τs=−∂H^lib‴∂θ=−ℏNβ−1.

The optimum shift will be found for θ=π/2, where τs=−ℏNγeB so the largest single spin torque can be ≈10−25 N·m.

Let us consider a particle with a diameter of 15 m undergoing Brownian motion in a harmonic trap under 0.1 mbar. This sensitivity is far from enabling single spin torque detection in a reasonable amount of time. Reference ^[31][45] reported the observation of spin-torque in this parameter regime, albeit using 109 spins that were all identically coupled with the libration. Figure 3b demonstrates mechanical detection of the ≈10−19.

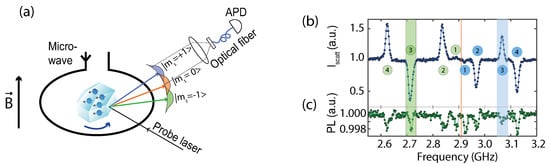
In order to approach the single spin torque level, particles with much smaller moment of inertia must be used. A levitating particle with a diameter of 100 nm and a modest Q factor of 104 would be sufficient to reach sensitivities in the 10−25 N·m/Hz range. Single-spin torque could then be discerned within one second in this experimentally achievable regime.

A similar discussion can be made to estimate the magnitude of the magnetic force on the CoM of a trapped diamond subjected to a magnetic field gradient (16)Fs=−∂H^com∂z=−ℏNγe∂Bz∂z.

Under a gradient of 105 T/m, one finds a single-spin force of 10−19 N. These large gradients typically require trapped micron-size magnets a few hundreds of nanometers from the NV center. Although less attractive for quantum applications, ensembles of spins could be used to bypass this technical difficulty.

The spin-dependent force has not been observed thus far using NV− centers to the best of our knowledge, even with large ensembles of spins. Even if strong magnetic field gradients can be achieved, it may induce a large inhomogeneous broadening when using ensembles, which will forbid efficient microwave excitation of the whole ensemble of NV− centers in the selected orientation. The magnetic field gradient will thus be bounded by the microwave excitation Fourier width δν in a pulsed excitation scheme, so that ∂Bz/∂z|max= Note that Δν can reach more than 100 MHz using high power amplifiers and dedicated fast electronics ^[32][95].

One further difficulty with NV centers coupled with trapped particles is to distinguish the center of mass motion from spin-induced torques. Indeed, a magnetic field offset is required in order to magnetize the NV− centers with a microwave which will rotate the trapped particle. The spin-induced angular displacements may thus contribute at the same level as the center of mass shifts, which complicates measurement analyses. This is a notoriously difficult task when using levitating particles where the angle between the diamond crystalline axes and the main trap axes cannot not always be controlled.

Let us conclude by adding that single-spin forces were measured using Magnetic Resonance Force Microscopy (MRFM) in ^[33][96]. Acquisition times of many hours and carefully engineered modulation techniques were employed. It is likely that significant progress can be made by applying these techniques to spin-mechanics with NV centers, with fascinating prospects for controlling the motion of micro-objects using single long-lived qubits.

4. Challenges Ahead for Levitated Spin-Mechanics

The negatively charge NV− center in diamond is a system of choice because of its robustness, which partly explains its increasing use in present quantum technologies. Nevertheless, recent experimental implementations have raised some technical difficulties. To date, optical trapping of diamond has been reported only above mbar pressures ^[34][98], while electrodynamics and diamagnetic traps operate in the 10−3 to 10−4 mbar range ^[35][36][34,36]. Furthermore, the control of diamond in terms of shape, size, and properties is not as straightforward as for silica, for example, where chemical processes allow the production of mono-disperse spherical particles.

The most promising technique for achieving flawless diamonds is chemical vapour deposition (CVD). In the different growth methods, the NV concentration is controlled using different strategies that depend on the initial nitrogen content in the diamond. When the sample contains large nitrogen concentrations, it can be irradiated by electrons or alpha particles to create vacancies. When starting with pure CVD diamonds, nitrogen is first implanted and converted to NV− centers, with a few percent yield, during an annealing process.

As discussed previously, thanks to the development of CVD grown diamonds and implantation techniques, it is possible to finely control the purity, and the number of hosted NV− centers in the diamond. Over the last decades, nano and micro-fabrication of diamond has enabled the realization of increasingly complex diamond structures ^[37][100]. Pillars of a controlled aspect-ratio can be nano-fabricated, and even more advanced structures are achievable using reactive ion etching technics. This is of particular interest for trapping diamonds with large librational frequencies ^[38][46].

The development of coated diamond initially intended for biology applications may also increase the achievable control of the properties of trapped diamond. A typical example is silica embedded diamonds, which allows obtaining spherical particles, and that have been shown to favor the NV− centers luminescence stability in optically levitated nano-diamonds ^[19][63].

Spin-mechanics with trapped objects will thus benefit from the tremendous progress in diamond material science and continuously improved knowledge about diamond and NV− centers. A potential drawback is that the production quantity of diamonds may be limited. In both cases, statistical trapping procedures that start from a sprayed colloidal particle solution, and rely on random trapping events are not ideal. The different recent approaches proposed for in situ trapping, using a piezo shacking, a laser impulsion ^[39][40][48,101], or trapping particles embedded in a polymer thin film [36], are very encouraging for the developments of on-demand trapping.

We have seen that increasing the number of NV− centers that couple to the oscillator motion is a viable route towards observing strong spin–mechanical effects. While the optimal density of NV− centers is generally a compromise between sensitivity and coherence time T2*, other more exotic effects start to appear when the spin density reaches a critical point.

For concentrations that are larger than ∼1 ppm (corresponding to a mean distance between spins of ≈15 nm or a dipolar coupling strength of ≈15 kHz), the dipolar coupling amongst NV spins plays an important role. One important effect is the modification of the spin lifetime T1 through dipolar coupling with other short lived NV− centers ^[41][42][43][66,102,103]. This particular effect has been used with a levitating diamond in a Paul trap to observe a resonant change in the spins’ magnetic susceptibility ^[44][83].

Other collective effects between NV− centers include the cooperative enhancement of the NV− centers’ dipole interaction, a phenomenon similar to that of super-radiance described in ^[45][46][47][71,72,73], and observed with a levitating diamond in an optical tweezer by Juan et al. ^[48][74].

Numerous studies have reported an increase in levitated diamond internal temperature under vacuum conditions ^{[24][49][50][51]}[53,55,104,105]. This heating is detrimental for practical reasons since it may lead to the burning or melting of the levitated particle. Internal temperature also induces extra quantum decoherence channels, which may prevent the observation of macroscopic quantum effects and impact the contrast of the spin resonance.

This heating was shown to be induced by laser absorption by the particle. The final temperature is the result of a competition between absorption, heat conduction to the surrounding residual gas, and black-body radiative exchange. Figure 4a shows the expected internal temperature for different diamond materials using the model detailed in references ^[52][34][4,98]. It can be seen that the expected final temperature can vary by one order of magnitude depending on the purity of the diamond material.

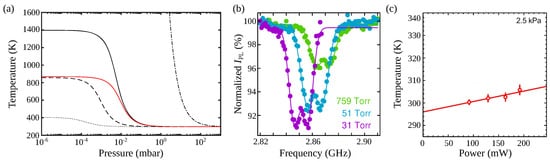
Studies conducted on high purity CVD bulk diamonds have shown that a very low laser absorbance is achievable ^[53][106], even below the silica absorption levels. Currently however, most experiments with levitated diamonds observe orders of magnitude higher heating rates. First, NV− color centers may contribute to the absorption due to non-radiative pathways of the electron population (dashed lines in Figure 4a). Most importantly, other diamond matrix defects will also play their role, from isolated nitrogen atoms to graphite on the diamond surface, through grain boundary or other atomic impurities ^[54][107].

The spin of the NV− centers is actually an invaluable tool to estimate the diamond temperature ^[49][50][55][55,104,108] because the zero-field splitting D, between ms=0 and ms=±1 states is temperature dependent, and well characterized ^[56][109]. One can measure the internal temperature of a levitated diamond by measuring the ESR of the NV− centers it hosts ^[49][50][55,104], see Figure 4b,c which shows heating measurements from trapped diamonds under vacuum.

Note that instead of improving the properties of trapped diamonds that are destined to be trapped under a magnetic field produced by a fixed magnet, the roles of the diamond and the magnet can be reversed. Schemes already discussed in this review ^[22][23][35,70] involving trapped magnets were recently proposed. In these proposals, the diamond containing NV− centers is attached to a large heat sink, so it does not heat up significantly and can readily be made from CVD for improved spin-properties. Furthermore, no strong laser needs to be shone onto the trapped magnet.

The present review focused on NV− centers in diamond, which is by far the most studied system for levitated spin-mechanics. However, our discussions may be applied to other color centers with similar behavior, and also solve some of the issues discussed in this section. Typically, over recent decades, color centers in SiC have been shown to own an optically addressable spin resonance ^[57][110]. Ultimately, with the recent isolation of single color centers ^[58][111], even silicon may become an excellent platform for spin-mechanics.