Encyclopedia
Please note this is a comparison between Version 1 by Pradip Gatkine and Version 3 by Peter Tang.
Astrophotonics is the application of photonic technologies to channel, manipulate, and disperse light from one or more telescopes to achieve scientific objectives in astronomy in an efficient and cost-effective way. Utilizing photonic advantage for astronomical spectroscopy is a promising approach to miniaturizing the next generation of spectrometers for large telescopes.
- astrophotonics
- arrayed waveguide gratings
- echelle gratings
- single-mode
- near-IR
- photonic lanterns
1. Introduction
The field of photonics has become an indispensable component of modern-day communication technology. The developments and demands from the telecommunication industry has driven a major boost in photonic technology and vice-versa in the last 35 years. Both fundamental and applied sciences have benefited from and contributed to the age of photonics. The platform of guided light in fibers and waveguides has opened the gates to next-generation instrumentation in astronomy. At the same time, the spin-offs from astrophotonics are extensively being adapted in other streams of science and technology.
The field of astrophotonics revolves around collecting astronomical light into guided channels, manipulating the transport and reconfiguration of the light, and filtering/dispersing/combining the guided light. A combination of one or more of these functionalities has led to a wide spectrum of astrophotonic instruments. They serve the purpose of leading new astronomical investigations or making the current investigations more efficient and cost-effective. Some of these scientific frontiers are: Detailed kinematic studies of galaxies [1], observing faint sources in the early universe [2], discovering and characterizing exoplanets and their atmospheres [3], and studying the first galaxies in the universe [4]. Following these pursuits requires large telescopes and innovative ways to manipulate the light to extract the most information from a limited number of photons.
The next two decades will mark the age of thirty-meter scale telescopes [5][6][5,6]. However, the volume, mass, and cost of conventional optical instruments grow as D2–D3 D2
–D3
(where D is the diameter of the telescope), creating new challenges for instrumentation [7]. At the same time, there is an explosion in the number of large astronomical surveys discovering a multitude of new transients, exoplanets, and galaxies. This necessitates development of new instruments for large telescopes that are compact and cost-effective while providing the flexibility to address the challenge of high-throughput characterization for these large surveys.
Photonic technologies provide a promising platform for building next-generation instruments that are flexible (in terms of light manipulation), compact (volumes of a few tens of cubic centimetres) and lightweight (a few hundreds of grams), thanks to manipulation of guided light [8][9][8,9]. In addition, they are cost-effective, due to the advantages of mass-fabrication. 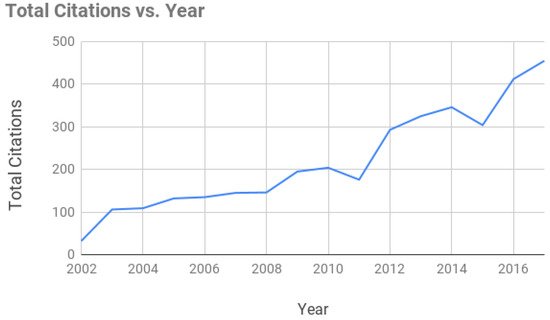Therefore, the astronomical community has pursued this direction very positively and built a wide variety of instruments from the near-ultraviolet (NUV) [10] to mid-infrared (MIR) wavebands [11]. As an example of the growth of astrophotonics, Figure 1 shows the number of citations of papers related to astrophotonic spectrographs. However, the current technical know-how is still far from complete or ideal, leaving many challenges that will likely be addressed in the near future.
Figure 1. Total number of new citations to papers in the field of astronomical spectroscopy using photonics. The publication data was obtained from the Web of Science interface (http://apps.webofknowledge.com).
2. Guiding the Light
The developments in the photonic industry and fabrication techniques in the last two decades have led to diverse adaptations of photonics optimized for the photon-starved field of astronomy. In order to use photonic advantage, the first step is to focus the light collected by the telescope onto a fiber, which is then used to efficiently carry the light to the spectrograph or other instruments.
2.1. Light Pipes
Historically, one of the first applications of these photonic dividends from communication industry came in the form of fiber fed (conventional) spectrographs [12]. The simple concept of using an optical fiber to carry the light from the focal plane of the telescope to the spectrograph slit imparted immense flexibility to astronomical spectroscopy in several aspects: a) Size: compact solution for multi-object spectroscopy; b) modularity: the use of fibers isolates the spectrograph from the telescope, enabling quicker change of instruments; c) mechanical stability: due to isolation of the spectrograph, its alignment is more stable and immune from changes in the telescope orientation; d) improved image stability due to image scrambling that occurs due to thousands of uncorrelated total internal reflections; e) improved spectral calibration due to consistency of the illumination pattern between the source, flat field, and calibration sources.
These features of fiber feeding led to significant developments in multi-object spectroscopy and fiber-fed integral field units. The fiber feeding was limited almost exclusively to optical and near-IR wavebands (0.3–2.4 μμ
m) due to the absorption properties of fused silica which is the principal material used in optical fibers [13].or Recently, fibers with new materials such as lithium niobate and fluoride glasses (e.g., ZBLAN glass), and chalcogenide glasses (e.g., gallium lanthanum sulphide glass) are being developed in orde to extending this range to 10 μm for spapace-based applications [13]. On the other hand, NUV guiding (∼190–300 nm) has been enabled by high OH-content fibers [14].
A key aspect in the design of fibers to capture the focused light is the number of modes supported by the fiber, which in turn depends on the refractive index gradient and the cross section of the fiber. The astronomical light received at the focus of a ground-based telescope is seeing-limited for optical and near-IR wavebands (i.e., the FWHM of the spot size is governed by atmospheric turbulence and not the diffraction limit). Capturing the large spot size with maximal coupling efficiency requires the use of large multimode fibers (MMFs, ∼several tens of modes). Although they act as light pipes, they are not suitable for any photonic manipulation of the light (such as filtering, interferometry, and spectroscopy in the photonic realm). The key reason is that most of these technologies, primarily inherited from the telecommunication industry, are developed for single-mode fibers (SMFs) which only propagate the fundamental mode, unlike MMFs which propagate multiple modes with different refractive indices.
2.2. Single-Mode Coupling
Single-mode operation is critical for certain precision measurements, such as exoplanet radial velocity [15][16][17][15,16,17]. With the advent of adaptive optics (AO) to correct for atmospheric aberrations, the spot size is reduced (i.e., higher Strehl ratio) to allow few-mode fibers to capture the focused light [18][19][18,19]. Moreover, coupling the AO-corrected light on a SMF has recently been demonstrated using a lenslet array of off-axis parabolic mirrors with a coupling efficiency of ∼25% in the Y-band (970–1070 nm) [20] and in the R-band (570–720 nm) [21].
With recent developments in extreme AO in concert with phase-induced apodized aperture (PIAA) lenses, a coupling efficiency as high as ∼74% has been demonstrated in the H-band (1500–1600 nm) for coupling the focused light into a single-mode fiber [22][23][24][22,23,24]. This is close to the maximum achievable coupling efficiency in such a system with apodization in the diffraction limit (∼90%). Despite these developments, it is more convenient and economical to capture the light in a bundle of few-mode fibers and use the concept of photonic lanterns [25][26][25,26] to transition the few-mode fibers to SMFs [18], since at present extreme AO is effective for only bright astronomical sources in the NIR bands (e.g., i-band magnitude of <9).
2.3. Photonic Lanterns
The concept of photonic lanterns emerged from the need to efficiently combine the light-capturing efficiency of MMFs and the light manipulation flexibility of SMFs [25]. A photonic lantern is essentially a MMF adiabatically tapering into a set of SMFs, allowing a low-loss transition. For highest efficiency, the number of SMFs should be the same as number of modes supported in the MMF, but fewer SMFs could be used if the efficiency requirement is lower [26][27][26,27]. The technology has since matured to lead to several variants. The key categories include: a) A MMF to a bundle of SMFs, with a demonstrated efficiency of ∼85–90% in the H-band [28][29][30][28,29,30]; b) a MMF to a multi-core fiber with an array of identical SMFs [29]; and c) an integrated photonic lantern, in which the transition from a multimode waveguide to many single-mode waveguides is inscribed in a glass block using ultra-fast laser inscription (ULI) [31][32][31,32]. While initially produced in the J (1100–1300 nm) and H bands (1400–1700 nm), photonic lanterns are now being developed in the mid-infrared bands as well using femto-laser inscription [33].
In addition to conveniently allowing single-mode functionality with the astronomical light, photonic lanterns also make it possible to reformat the beam in many ways by rearranging the output single-mode fibers (e.g., in a slit form or closed packing [27] ) for the next instruments in the pipeline (e.g., a diffraction-limited spectrograph or an interferometer) [34][35][36][34,35,36].
3. Filtering and Combining the Light
Before the captured and guided light (in SMFs) is fed to a photonic spectrograph, it can be further conditioned depending on the scientific objective of the astronomical observation as well as the waveband of interest.
3.1. OH-Emission Suppression
Ground-based NIR spectroscopy faces the problem of bright NIR background due to a series of narrow (∼0.1 nm) emission lines (telluric lines) from atmospheric hydroxyl (OH) molecules [37]. Background subtraction is very difficult, due to short-timescale fluctuations in the brightness of these lines, making observations of faint sources impractical. This problem is pronounced in the J (1100–1300 nm) and H bands (1400–1700 nm). Sending this background-dominated light to a low/moderate resolution spectrograph (with resolution element > 0.05 nm) leads to scattering of the bright background which is difficult to remove after the fact. An improved background subtraction requires suppression of these lines before it interacts with the dispersing optics. A promising way to suppress these emission lines before dispersion with high rejection ratio and low loss is using Bragg gratings in single-mode fibers [30].δλ
3.2. Interferometry
In certain astronomical studies, such as measuring the stellar diameters and observing exoplanets, it is crucial to achieve high-resolution imaging and/or suppress light from a bright star next to a faint planet. For ground-based observations, the necessity of high spatial resolution requires combining light from two or more telescopes. In the past, the technique of interferometry has been used to measure stellar radii using two or more telescopes separated by a distance D, to allow ∼λ/D angular resolution [48]. Another way, called aperture masking interferometry, achieves the diffraction limit through artificially created sub-apertures formed by segmenting the telescope pupil [49,50]. The image (i.e., brightness distribution) is reconstructed using Van Cittert–Zernike theorem, which states that the spatial coherence function of light is the Fourier transform of the angular brightness distribution of the light source [51]. Integrated photonic reformatters and interferometers have recently been developed with compact designs, better phase control, and mechanical/thermal stability [52].
4. Dispersing the Light
The astronomical light guided in the single mode fibers can be dispersed in many ways, most of which are inherited from the telecommunication technique wavelength division multiplexing (WDM). This technique emerged from the need to increase the data density of the existing fiber-optic networks by using multiple wavelengths to carry multiple data packets simultaneously. Thus, a variety of photonic platforms were developed to combine different wavelengths (multiplex) and disperse them (de-multiplex).
