Learning-Assisted Rain Attenuation Prediction Models

Learning-Assisted Rain Attenuation Prediction Models: Comparison

Please note this is a comparison between Version 4 by Bruce Ren and Version 3 by Bruce Ren.

Rain attenuation becomes significant to degrade the earth-space or terrestrial radio link’s signal-to-noise ratio (SNR). So, to maintain the desired SNR level, with the help of fade mitigation techniques (FMTs), it needs to control transmitted signals power considering the expected rainfall. However, since the rain event is a random phenomenon, the rain attenuation that may be experienced by a specific link is difficult to estimate. Many empirical, physical, and compound nature-based models exist in the literature to predict the expected rain attenuation. Furthermore, many optimizations and decision-making functions have become simpler since the development of the learning-assisted (LA) technique. In this work, the LA rain attenuation (LARA) model was classified based on input parameters. Besides, for comparative analysis, each of the supported frequency components of LARA models were tabulated, and an accurate contribution of each model was identified. In contrast to all the currently available LARA models, the accuracy and correlation of input-output parameters are presented. Additionally, it summarizes and discusses open research issues and challenges.

rain attenuation
survey
machine learning

1. Introduction

A recent analysis has shown that approximately 50 billion devices will need an Internet connection by 2020; most of them will be wirelessly connected ^[1]. Rapidly emerging wireless networking systems are beginning to use millimeter-wave frequency bands (30–300 GHz) to transmit data at a growing pace due to the demands of mobile data network service providers.

The rain has a substantial effect on electromagnetic wave propagation. This effect influenced researchers by controlling transmitted power to the counteraction of rain influence on the radio waves. Thus, several experiments on the approximation of rain attenuation techniques have been carried out worldwide. The rain attenuation research is used to study and predict attenuation over a wide variety of frequency bands, especially for bands above 10 GHz ^[2], in various geographical areas and to identify a suitable model that can estimate attenuation. Identifying the features of a rain attenuation model is one of the most critical activities for the creation of a model. Several variables can affect rain attenuation, such as the transmitter’s distance from the receiver, frequency, rainfall intensity, temperature of precipitation, humidity, density, wind speed, and wind direction. However, among the parameters, rain rate and path length are the most important factors. As a result, most rain attenuation models evaluate the relationship between rain rate and path length parameters to rain attenuation.

In order to plan the channel capacity, manage the connection quality, and network design, reliable rain attenuation in a specific radio link is necessary. Often, if other structures of a communication system operate properly, accessing the possibility of terrestrial or inclined links can be improved with an efficient rain attenuation model. It is also possible to avoid overestimating the transmission system’s necessary power by the estimation through the rain attenuation model.

Besides, it is important to meet the spectrum management regulatory organization specification in each frequency range to comply with the permissible requirements for power transmission. In the case of these requirements not being met, the transmitted signal power can interfere with another neighboring frequency band. This intrusion can cause disruptions to neighboring telecommunications equipment.

2. Preliminaries

It is reported that the ANN/ML-based rain attenuation model can adopt many parameters compared to the physical or empirical-based models. In this section, a discussion regarding several parameters of LARA models and the algorithms used in these models is provided.

2.1. The Factor of LARA Models

The rationale-cause-based analysis must first be sought in order to develop a good rain attenuation model. In other words, it means finding the factors that affect the rain attenuation. Although the rainfall rate is the most important factor determining attenuation, other factors also possess significance as per several studies. A brief review is presented here regarding more rain attenuation factors.

Lina Zhao et al. ^[3] listed 10 factors that could affect rain attenuation in the radio link at the frequency component above 10 GHz. The factors include temperature, path length, frequency, precipitation rate, wetness, wind speed, direction, and visibility of the wind. Alencar et al. ^[4] considered the polarization angle, frequency, station height, height precipitation rate (time percentage), elevation angle, and latitude can affect the attenuation of rainfall.

Thiennviboon et al. ^[5] considered the precipitation intensity, frequency, latitude, the angle of elevation, and azimuth as attenuation factors for the earth–space link. Mpoporo et al. ^[6] consider the precipitation rate, azimuth, elevation angle, precipitation height, the percentage of time exceedance, and frequency as a slant link factor as parameters that impact attenuation. V. Kvicera et al. ^[7] claimed that the rainfall rate and several parameters can affect the rain attenuation, such as moisture and air pressure, wind direction, and wind speed. S. Livieratos et al. ^[8] developed a supervised machine learning model to take the frequency, rain rate, polarization, and path length as features from the International Telecommunication Union Radiocommunication Sector (ITU-R) database.

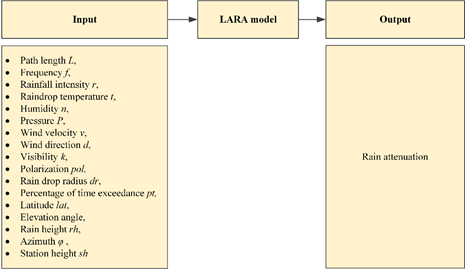
Apart from the link length and precipitation rate, most factors may have less influence on rain attenuation, but in order to achieve the highest level of predictive accuracy, it may be necessary to consider such loosely affecting factors in the model. Figure 2 presents a general illustration of the LARA model’s input and output parameters. From now and onwards, we will use parameters or features or factors as of equivalent meaning.

2.2. Algorithms Used in LARA Models

Several types of learning-aided algorithms are used to estimate rain attenuation via the LARA models. Mostly, the algorithms used here are a modified version of the back-propagation algorithm and a basic structure of an artificial neural network. Table 1 presents all the learning techniques used for attenuation prediction to date as per the best of our knowledge in major scientific publication database records accessed till July 2020.

2.3. Critical Challenges of LARA Models

The critical challenge of predicting the rain attenuation model compared to the other time-varying model is that there are at least reported 17 input features (Figure 1) that can influence rain attenuation. Although few of these features are a fixed quantity in a particular infrastructure setup, such as station height, azimuth, latitude, polarization, or elevation angle, many of the features have statistical variant behavior, such as rainfall intensity, wind velocity, pressure, raindrop temperature, and raindrop size. Many of these features change over time to time, which may be called statistical variations. The adjustment of these statistical variations may lead to undesirable nonlinear properties in univariate time series. Many of the statistical variation components and nonvariational components are not independent, and thus not separable ^[9].

Figure 1. A general illustration of the LARA model’s input and output parameters.

Figure 1. A general illustration of the LARA model’s input and output parameters.

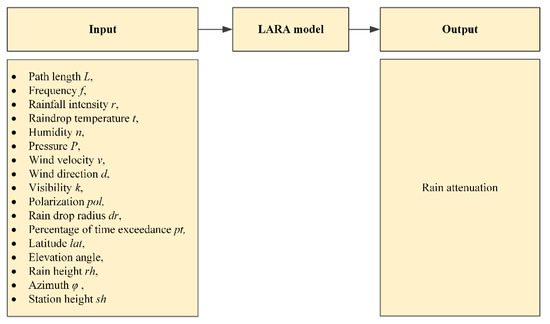
Table 1. Learning algorithms used in currently published LARA model’s rain attenuation model.

Ref.	Learning Models	Model Structure
^[4]	Single-layer feed-forward back-propagation (SL FFBP) model	Back-propagation single layer neural model with a single hidden layer.
^[6]	Feedforward back-propagation neural network (FFBNN)	Feedforward back-propagation neural network
^[8]	Supervised machine learning (SML)	SVM and SML-based regression algorithm that uses Gaussian process-compatible kernel functions.
^[10]	Artificial neural network (ANN) and k-nearest neighbor (kNN)	kNN and ANN (recurrent neural network)
^[11]	Back-propagation neural network (BPNN)	BPNN with a sigmoid input function
^[12]	Feed-forward multilayer perceptron (FFMLP) in addition to supervised learning (SL)	The network is the multilayer feed-forward (MFF) network; Input section: Bayesian regularization adaptive training algorithm; Activation function: Tangent sigmoid transfer functions (hidden layer) and pure linear transfer function (output layer).
^[13]	Least squares-support vector machine (LS-SVM) and BPNN	BPNN: with M layers and N number of nodes
^[5]	Single-layer artificial neural network (SL ANN)	LS-SVM: Using LS-SVM to develop a function that can predict attenuation with an unseen rain rate.
^[14]	In situ learning algorithm (ILA) and adaptive artificial neural network (AANN)	SL ANN: It is a single hidden layer network. Activation function: hyperbolic-tangent activation function (hidden layer with 5–9 nodes), and linear activation function (output node)
^[15]	Regression analysis (RA)*	Regression analysis

*This technique determines specific attenuation coefficient (k and α) rather than predicting the attenuation; consequently, we have limited its use in the later section.

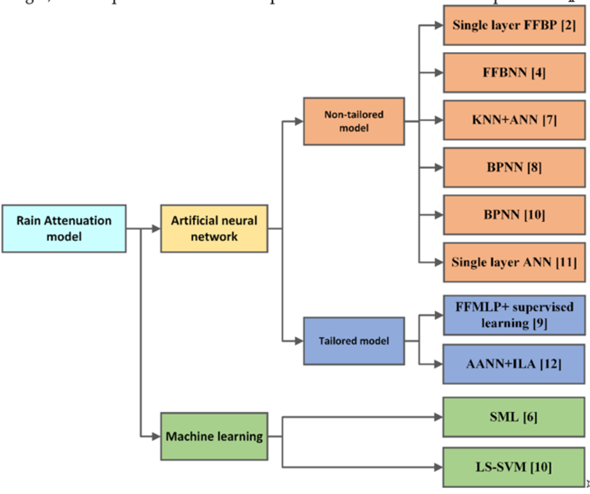
3. Taxonomy

The LARA models are somehow different compared to the traditional rain attenuation models. As the LARA models possess the property like a black-box, and physical significance represents the model input parameters to the output rain attenuation parameters, LARA models can take several input parameters. Whereas, it is complicated to handle many input parameters by an ordinary algorithm-based rain attenuation model. The LARA model can be classified in different perspectives, such as the model structure and training data set.

Based on the model structure, the existing LARA model can be classified into two broad categories: artificial neural network (ANN) and machine learning approach. The ANN-based models can be further classified into two types: tailored and non-tailored model. The tailored model structure is built on a customization style whereas the non-tailored model is almost the basic structure as per its name in the literature. Figure 2 shows the LARA model’s classifications based on the model structure.

Figure 2. LARA model’s taxonomy based on the model structure or formation.

References

Boubiche, D.E.; Pathan, A.K.; Lloret, J.; Zhou, H.; Hong, S.; Amin, S.O.; Feki, M.A. Advanced Industrial Wireless Sensor Networks and Intelligent IoT. IEEE Commun. Mag. 2018, 56, 14–15.
Semire, F.A.; Mohd-Mokhtar, R.; Akanbi, I.A. Validation of New ITU-R Rain Attenuation Prediction Model over Malaysia Equatorial Region. MAPAN 2019, 34, 71–77.
Wu, J.; Chen, L.; Zheng, Z.; Lyu, M.R.; Wu, Z. Clustering web services to facilitate service discovery. Knowl. Inf. Syst. 2014, 38, 207–229.
Alencar, G.A. Low statistical data processing for applications in earth space paths rain attenuation prediction by an artificial neural network. In Proceedings of the 2004 Asia-Pacific Radio Science Conference, Qingdao, China, 24–27 August 2004; pp. 344–346.
Thiennviboon, P.; Wisutimateekorn, S. Rain Attenuation Prediction Modeling for Earth-Space Links using Artificial Neural Networks. In Proceedings of the 2019 16th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Pattaya, Thailand, 10–13 July 2019; pp. 29–32.
Mpoporo, L.J.; Owolawi, P.A.; Ayo, A.O. Utilization of Artificial Neural Networks for Estimation of Slant-Path Rain Attenuation. In Proceedings of the 2019 International Multidisciplinary Information Technology and Engineering Conference (IMITEC), Vanderbijlpark, South Africa, 21–22 November 2019; pp. 1–7.
Kvicera, V.; Grabner, M. Rain Attenuation at 58 GHz: Prediction versus Long-Term Trial Results. Eurasip J. Wirel. Commun. Netw. 2007, 2007, 046083.
Livieratos, S.N.; Cottis, P.G. Rain Attenuation Along Terrestrial Millimeter Wave Links: A New Prediction Method Based on Supervised Machine Learning. IEEE Access 2019, 7, 138745–138756.
Hylleberg, S. Modelling Seasonal Variation. In Nonstationary Time Series Analyses and Cointegration; Oxford University Press: Oxford, UK, 1994; pp. 153–178.
Li, T.; Suzuki, K.; Nishioka, J.; Mizukoshi, Y.; Hasegawa, Y. Short-term rainfall attenuation prediction for wireless communication. In Proceedings of the 2015 IEEE 16th International Conference on Communication Technology (ICCT), Hangzhou, China, 18–20 October 2015; pp. 615–619.
Ahuna, M.; Afullo, T.; Alonge, A. Rain attenuation prediction using artificial neural network for dynamic rain fade mitigation. Saiee Afr. Res. J. 2019, 110, 11–18.
Amarjit; Gangwar, R.P.S. Implementation of Artificial Neural Network for Prediction of Rain Attenuation in Microwave and Millimeter Wave Frequencies. Iete J. Res. 2008, 54, 346–352.
Zhao, L.; Zhao, L.; Song, Q.; Zhao, C.; Li, B. Rain Attenuation Prediction Models of 60GHz Based on Neural Network and Least Squares-Support Vector Machine; Zhang, B., Mu, J., Wang, W., Liang, Q., Pi, Y., Eds.; Springer International Publishing: Tianjin, China, 2014; pp. 413–421.
Roy, B.; Acharya, R.; Sivaraman, M.R. Attenuation prediction for fade mitigation using neural network with in situ learning algorithm. Adv. Space Res. 2012, 49, 336–350.
Singh, H.; Kumar, V.; Saxena, K.; Bonev, B. An Intelligent Model for prediction of Attenuation caused by Rain based on Machine Learning Techniques. In Proceedings of the 2020 International Conference on Contemporary Computing and Applications (IC3A), Lucknow, India, 5–7 February 2020; pp. 92–97.