1. Introduction

Technological development in the past decades led to the increase in demand for novel cooling fluids able to surpass the conventional ones—air and water—to improve the lifespan of the electronic components [1]. One type of fluid that has been increasingly investigated is nanofluid (NF), as seen in Figure 1. Introduced in 1995 by Stephen Choi, nanofluids consist of a colloidal dispersion of nanoparticles (NPs) with 1–100 nm of dimension in a base fluid (BF) ^[2][3][2,3].

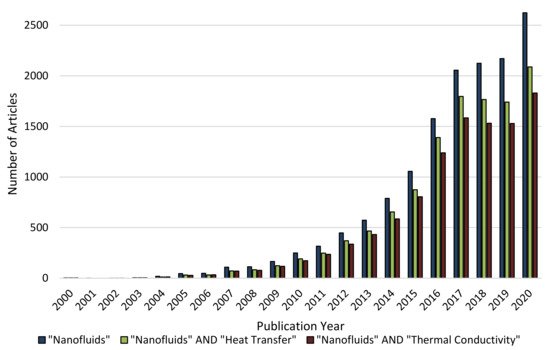
Figure 1. Number of scientific journal articles presented in the Science Direct database published between January of2000 and September of 2020.(Search date: 10.09.2020) (Please read the data availability statement).

The NPs usually used in the NFs are oxides, metals, nitrides, and non-metals like carbon nanotubes and graphene, while the BF are often water, ethylene glycol, oils, and polymer solutions [4].

NFs contribute to the improvement of heat transfer processes, and to reduce and optimize thermal systems [5].Different properties, such as wettability and thermal conductivity, can be adjusted by altering the NPs concentration, making nanofluids suitable for a wide range of applications. Local concentration can be controlled using magnetic NPs under the action of an applied magnetic field [6]. Nevertheless, preparation and use of NFs still have some limitations. Sedimentation and aggregation of the particles are difficult to control and may accelerate corrosion of the components and increase the dynamic viscosity of the NFs. Also, the synthesis of nanomaterials is still an expensive process [5].On top of that, there is no general consensus regarding the exact concentration and type of particle required for the NFs best performance. In spite of these difficulties, new and more competitive preparation techniques have been developed. For example, titanium dioxide NFs can be obtained nowadays by the Vapor Deposition Technique (VDT) [7].

Due to the previously mentioned advantages, NFs have been applied to a wide variety of fields ^[6][7][8][9][6,7,8,9]. For instance, some NFs were used to cool electronic parts such as CPUs [10] and transformers [11], motor engines [12] and nuclear reactors [13]. In space technologies, they were tested to improve cooling mechanisms, and also as fuel [14] and for machining and grinding techniques as lubricant and cutting fluid [15]. The thermal properties of NFs were also very useful to improve the heat transport and, consequently, the thermal efficiency of systems like heat pipes [16], thermosiphons [17], heat exchangers, and chillers ^[6][8][6,8], and solar panels and collectors [17]. Recently, there has been a growing interest in the use of NFs in nanomedicine. On this field, the magnetic NPs can be used not only to improve the potential of diagnostic techniques but also in hyperthermia treatments or as drug carriers ^{[18][19][20][21]}[18,19,20,21].Also, the use of NFs to study the heat transfer mechanisms in cavities, like the free natural convection, has grown tremendously [22].

One of the most relevant properties of NFs is the thermal conductivity. The thermal conductivity of NFs is influenced by shape, size, concentration and surface resistance of the NPs and by the viscosity, pH, temperature, and other characteristics of the base fluid [23]. Several theoretical models and experimental methods were developed to measure this property. The most common measuring methods are the transient hot-wire method followed by the 3ω method, the steady-state parallel plate method and the temperature oscillation method. Despite the growing number of studies, there are still disparities between data generated by the theoretical models and experimental measurements as well as between measurements derived from the same method (reproducibility of results) [3].

2. Thermal Conductivity Measurements Overview

The current methods developed for thermal conductivity measurements are static methods and can be divided in Steady State Methods and Transient State Methods. The Steady State Methods comprise the parallel plane and coaxial cylinders methods, while the Transient State Methods include the transient hot wire, the transient plane source theory, the temperature oscillation method, the laser flash method and the 3ω method [24]. A brief description of the techniques will be presented in the following subsections. FigureFigure 2 2 shows the steady and transient state methods often used to measure the thermal conductivity of the NFs.

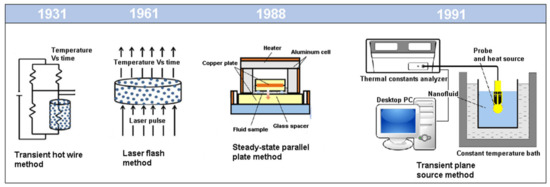
Figure 2. Schematic diagram of steady and transient state methods to measure the thermal conductivity of nanofluids (NFs) (Adapted from [5]).

2.1. Transient Hot Wire Method

In this technique, a very thin metal wire, usually of platinum or tantalum, is used as both heat source and sensor. The wire is submerged on the NF, and a certain voltage is applied through the wire, heating it. The heat will then be transferred to the surrounding liquid at a rate depending on the thermal conductivity of the liquid. The resistance variations measured in the wire can be correlated with the temperature variations and, therefore, the thermal conductivity is calculated. Systematic errors that might affect the measurements, such as errors resulting from natural convection, can be corrected experimentally ^[5][24][5,24].

2.2. Transient Plane Source Theory

A fast and sensitive technique with similar principle as the transient hot wire consists of replacing the wire by a hot disk. Similarly, to obtain the temperature and thus calculate the thermal conductivity, the time variation of the electrical resistance is recorded. Like in the case of the Transient Hot Wire Method, convection currents in the fluid might affect the measurements ^[5][24][5,24].

2.3. Temperature Oscillation

The fluid is placed in a cylinder with an oscillating temperature being applied at both ends. The amplitude and phase of the temperature oscillation in the middle of the cylinder are registered. To avoid interferences from the convection phenomena, the amplitude of the applied oscillation should be as small as possible ^[24][25][24,25].

2.4. 3ω Method

The metal heater in the fluid is heated by a sinusoidal electric current with an angular frequency of ω, leading to temperature oscillations in the fluid with a certain frequency. Then, the frequency is correlated with the thermal conductivity of the NF. This technique requires small amounts of fluid and is more suitable for non-spherical particles, according [5] are more suitable for nanotubes, nanowires, and nanofins. On the other hand, it takes more time than the other techniques to obtain the results ^[5][24][5,24].

2.5. Laser Flash Method

The bottom of the fluid is heated with a laser and the temperature on the top of the fluid is measured with a thermometer. The temperature increase can then be correlated with the thermal conductivity. The effects of radiation and convection are minimized by the short time (in the order of nanoseconds) needed to heat the sample [5].

2.6. Parallel Plate

The sample is placed between two round parallel plates made of copper with incorporated thermocouples. One of the plates is heated, and the temperature difference between the plates will be correlated with the thermal conductivity. To obtain a homogeneous thickness and to minimize convection due to gravity, both plates can be leveled while the sample is being loaded ^[5][24][5,24].

2.7. Coaxial Cylinders

The thermal conductivity of nanofluid can be calculated in the gap by using the Fourier equation in cylindrical co-ordinates. The natural convection is reduced by using very small temperature gradients [24].

3. Parameters That Affect Thermal Conductivity

The thermal conductivity of the NFs can be affected by several factors, since many preparation parameters can vary widely, as presented in the Figure 3. From the characteristics of the NPs to their stability in the fluid, as well as other properties of the suspension, all those factors contribute, directly or indirectly, to induce variations in the thermal conductivity. A brief description of the effect of each factor in the thermal conductivity will be presented in the following sub-sections.

The thermal conductivity of the NFs can be affected by several factors, since many preparation parameters can vary widely, as presented in the Figure 3. From the characteristics of the NPs to their stability in the fluid, as well as other properties of the suspension, all those factors contribute, directly or indirectly, to induce variations in the thermal conductivity. A brief description of the effect of each factor in the thermal conductivity will be presented in the following sub-sections.

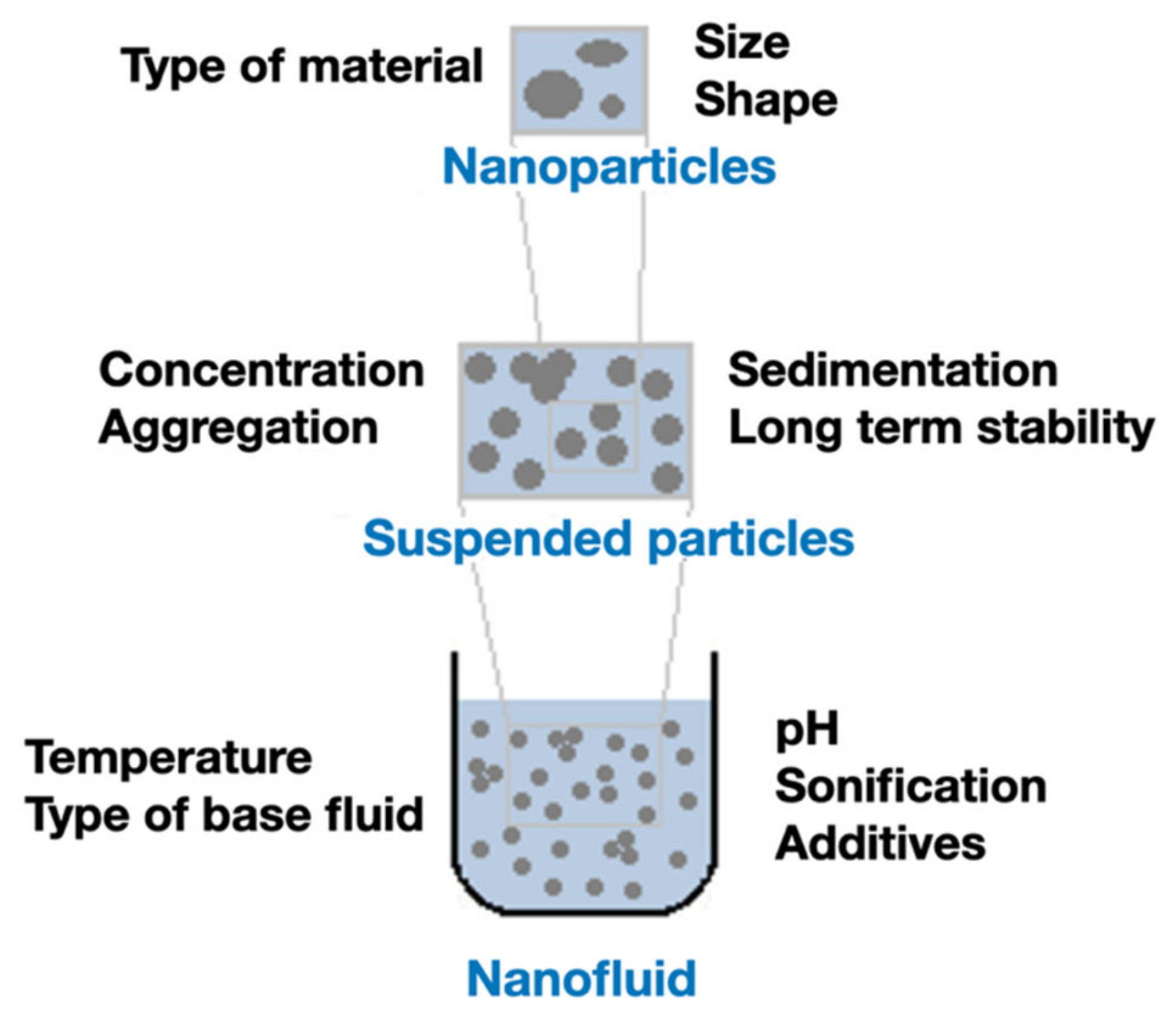
Figure 3.

Different properties that affect the thermal conductivity of NFs (Adapted from [5]).

3.1. Nanoparticles (NPs)

3.1.1. Type

Different types of NPs have been tested, such as metals, metal oxides, ceramics, and carbon nanotubes. Some reports indicate that the thermal conductivity of the NPs is less relevant to increase the NFs heat transfer rates, while others suggest that NPs with higher values of thermal conductivity may increase the heat transfer in the NFs [26]. For instance, Wang et al. [27] compared the thermal conductivity of water-based nanofluids with copper and alumina NPs. The greater enhancement of the thermal conductivity in the copper nanofluid was attributed to the higher thermal conductivity of copper. On the other hand, Yoo et al. [28] observed a greater enhancement in thermal conductivity using a water-based nanofluid with TiO

₂

NPs than when using Al

₂

O

₃

NPs, despite the lower values of the thermal conductivity of the TiO

₂

NPs.

3.1.2. Size

The influence of the size of the NPs is still controversial among the scientific community. Ambreen and Kim [29] believed that the reduction of the size of NPs increases the effective surface area, thickens the interfacial layering, and enhances the Brownian motion. For these reasons, the thermal conductivity of the nanofluids increases with the reduction of the particle diameter. Xu et al. [30] measured the thermal conductivity of water-based NF with Al

₂

O

₃NPs of different sizes and registered a reduction of the thermal conductivity with increasing sizes. Anoop et al. ^[31] also compared NFs with alumina NPs of 45 and 150 nm of dimensions. The higher enhancement was reported for the smaller particles. Although most of the results presented in the available literature agree with that proposition, a few others suggest opposite conclusions. Jang and Choi ^[32] registered an increase of the thermal conductivity with increasing particle size for different types of NPs. Timofeeva et al. ^[33] compared water-based NFs with four different sizes of SiC NPs and obtained higher values of thermal conductivity with the bigger particles. It should also be noted that for nearly micrometer-sized particles, the Brownian motion is not present, and the thermal conductivity remains unchanged. For a small range of particle size, some authors reported a linear increase of conductivity with increasing particle size due to the reduced interfacial thermal resistance of the larger particles ^[5][26].

NPs of different sizes and registered a reduction of the thermal conductivity with increasing sizes. Anoop et al. [31] also compared NFs with alumina NPs of 45 and 150 nm of dimensions. The higher enhancement was reported for the smaller particles. Although most of the results presented in the available literature agree with that proposition, a few others suggest opposite conclusions. Jang and Choi [32] registered an increase of the thermal conductivity with increasing particle size for different types of NPs. Timofeeva et al. [33] compared water-based NFs with four different sizes of SiC NPs and obtained higher values of thermal conductivity with the bigger particles. It should also be noted that for nearly micrometer-sized particles, the Brownian motion is not present, and the thermal conductivity remains unchanged. For a small range of particle size, some authors reported a linear increase of conductivity with increasing particle size due to the reduced interfacial thermal resistance of the larger particles [5,26].

3.1.3. Shape

Different shapes of NPs were tested in theoretical and experimental studies with NFs: spherical, cylindrical, rod, banana-shaped, nearly rectangular, brick, platelet, and blade shapes. The results obtained indicate that particles with larger aspect ratios contribute to the enhancement of the thermal conductivity, since thermal penetration increases and the adverse effects of interfacial thermal resistance on heat transfer are reduced. On the other hand, when the particles have a small sphericity factor, the thermal conductivity is not enhanced ^[5][26]. Murshed et al. ^[34] observed a greater increase in the thermal conductivity values of water-based TiO

Different shapes of NPs were tested in theoretical and experimental studies with NFs: spherical, cylindrical, rod, banana-shaped, nearly rectangular, brick, platelet, and blade shapes. The results obtained indicate that particles with larger aspect ratios contribute to the enhancement of the thermal conductivity, since thermal penetration increases and the adverse effects of interfacial thermal resistance on heat transfer are reduced. On the other hand, when the particles have a small sphericity factor, the thermal conductivity is not enhanced [5,26]. Murshed et al. [34] observed a greater increase in the thermal conductivity values of water-based TiO

₂

NFs when using rod-shape NPs than when using spherical NPs. Jeong et al. [35] obtained similar results when comparing spherical and nearly rectangular-shaped ZnO NPs. Timofeeva et al. [36] compared NFs with four different shapes of Al

₂

O

₃

NPs and concluded that the NF with higher thermal conductivity value was the one with cylindrical NPs, followed by the one with brick shape NPs. In addition, the NFs with blade shape and platelet shape particles presented similar values and were also the lower ones among the testing group. Glory et al. [37] investigated the increase of the thermal conductivity using Multi-Walled Carbon Nanotubes (MWCNT)of different lengths, obtaining greater values for the NFs with the longest nanotubes.

3.2. Suspension

3.2.1. Base Fluids

Most studies agree that the base fluids with greater thermal conductivity correspond to NFs with smaller thermal conductivity increases. The reports also suggest that the affinity of the fluid to the NPs has an important role in the thermal conductivity enhancements [26]. For instance, Gowda et al. [38], Chen et al. [39], and Hwang et al. [40] reported higher thermal conductivity values for ethylene glycol-based NFs than water-based NFs, using alumina, MWCNTs, and CuO NPs, respectively.

3.2.2. Concentration

The increase of the particle concentration enhances the thermal conductivity due to the greater interfacial area between the base fluid and the NPs and increasing agglomeration ^[41][42]. Rostamian et al. ^[43] and Xuan et al. ^[44] reported an increase in thermal conductivity by increasing the nanoparticle concentration. Jana et al. ^[45] also observed a linear relation between concentration and thermal conductivity using water-based copper NFs. Lee et al. ^[46], using NPs of Al

The increase of the particle concentration enhances the thermal conductivity due to the greater interfacial area between the base fluid and the NPs and increasing agglomeration [41,42]. Rostamian et al. [43] and Xuan et al. [44] reported an increase in thermal conductivity by increasing the nanoparticle concentration. Jana et al. [45] also observed a linear relation between concentration and thermal conductivity using water-based copper NFs. Lee et al. [46], using NPs of Al

₂

O

₃ and CuO, measured experimentally the thermal conductivity of the NFs at low volume fraction range (lower than 0.05%) and found that the thermal conductivity ratios increase almost linearly with volume fraction, but with different rates of increase for each group of NPs tested. However, some reports noted a reduction of the thermal conductivity for high concentration values. The stability of the NF is likely to play a major role in the determination of the ideal concentration ^[5][26].

and CuO, measured experimentally the thermal conductivity of the NFs at low volume fraction range (lower than 0.05%) and found that the thermal conductivity ratios increase almost linearly with volume fraction, but with different rates of increase for each group of NPs tested. However, some reports noted a reduction of the thermal conductivity for high concentration values. The stability of the NF is likely to play a major role in the determination of the ideal concentration [5,26].

3.2.3. Agglomeration

The agglomeration of particles contributes to the enhancement of the thermal conductivity by providing extra conduction paths on the NFs. For fluids with smaller particles, the aggregation is more prone to occur. The way the aggregation occurs in NFs with greater volume fractions depends on the shape of the particles. In the studies performed by Hong et al. ^[47], an increase of thermal conductivity was observed with an increase of the aggregation of the particles in a water-based alumina NF. On the other hand, large agglomerates of particles can lead to sedimentation of the particles and reduction of the thermal conductivity. Jana et al. ^[45] noted a decrease of thermal conductivity with increase sedimentation time in water-based copper and carbon nanotube NFs. It is possible to locally control the aggregation in NFs with magnetic NPs by means of a magnetic field. The aggregation is also reversible by applying different magnetic fields in different directions ^[5][26][48]. Li et al. ^[49] reported an enhancement in the thermal conductivity of an NF with iron particles when applying a magnetic field. Also, Nasiri et al. ^[50] observed a reduction of the thermal conductivity of a water-based carbon nanotube NF due to the aggregation of the NPs.

The agglomeration of particles contributes to the enhancement of the thermal conductivity by providing extra conduction paths on the NFs. For fluids with smaller particles, the aggregation is more prone to occur. The way the aggregation occurs in NFs with greater volume fractions depends on the shape of the particles. In the studies performed by Hong et al. [47], an increase of thermal conductivity was observed with an increase of the aggregation of the particles in a water-based alumina NF. On the other hand, large agglomerates of particles can lead to sedimentation of the particles and reduction of the thermal conductivity. Jana et al. [45] noted a decrease of thermal conductivity with increase sedimentation time in water-based copper and carbon nanotube NFs. It is possible to locally control the aggregation in NFs with magnetic NPs by means of a magnetic field. The aggregation is also reversible by applying different magnetic fields in different directions [5,26,48]. Li et al. [49] reported an enhancement in the thermal conductivity of an NF with iron particles when applying a magnetic field. Also, Nasiri et al. [50] observed a reduction of the thermal conductivity of a water-based carbon nanotube NF due to the aggregation of the NPs.

3.3. Nanofluids

3.3.1. Preparation Methods

Two methods of preparing nanofluids are commonly used by the scientific community, the one-step, and two-step method. The one-step method involves the production and dispersion of the NPs in the BF at the same time. For this reason, the process reduces the NPs agglomeration and increases stability in the NFs ^[3]. In contrast, the high cost and level of impurities on the NFs, according to Devendiran et al. ^[51], are the main disadvantages of this process. In the two-step method, first, the NPs are obtained and then added to the BF. This simplifies the manufacturing process while reducing its cost. However, maintaining the stability of the NFs is one of the challenges of this method. Some alternatives to solve the problem include the use of ultrasonic treatment, altering the pH of the suspension, adding surface activators or dispersants or a mixture of both ^[51][52].

Two methods of preparing nanofluids are commonly used by the scientific community, the one-step, and two-step method. The one-step method involves the production and dispersion of the NPs in the BF at the same time. For this reason, the process reduces the NPs agglomeration and increases stability in the NFs [3]. In contrast, the high cost and level of impurities on the NFs, according to Devendiran et al. [51], are the main disadvantages of this process. In the two-step method, first, the NPs are obtained and then added to the BF. This simplifies the manufacturing process while reducing its cost. However, maintaining the stability of the NFs is one of the challenges of this method. Some alternatives to solve the problem include the use of ultrasonic treatment, altering the pH of the suspension, adding surface activators or dispersants or a mixture of both [51,52].

The high production cost of the nanofluids has been another limitation, which may require a more demanding maintenance of a cooling system and, consequently, raise the operating costs. In addition, the preparation of NFs on a larger scale requires further reduction of its costs since the most cost-effective techniques are the ones considered for commercialization purposes. One way to reduce these costs is by recycling and recover NPs from industrial wastes.

3.3.2. Temperature

Some reports indicate that the thermal conductivity is enhanced with the temperature increase, while others reported a reduction of the thermal conductivity with the same effect. Few others stated that no changes were observed with temperature variations. For instance, Chon et al. [53] and Mintsa et al. [54] registered a dependent behavior between the thermal conductivity of the NFs and temperature, while Shalkevich et al. [55] reported an independent behavior. Duangthongsuk et al. [56], on the other hand, observed a decrease of the thermal conductivity with increasing temperature in a water-based TiO

₂ NFs. The enhancement of the thermal conductivity with increasing temperature is thought to be caused by the improvement of the Brownian motion and the reduction of the surface energy of the particles. On the contrary, a reduction of the thermal conductivity with increasing temperature was reported for NFs with non-spherical particles, which might indicate that the aspect ratio of the particle has a relevant influence ^[5][26].

NFs. The enhancement of the thermal conductivity with increasing temperature is thought to be caused by the improvement of the Brownian motion and the reduction of the surface energy of the particles. On the contrary, a reduction of the thermal conductivity with increasing temperature was reported for NFs with non-spherical particles, which might indicate that the aspect ratio of the particle has a relevant influence [5,26].

3.3.3. pH

The pH of the NFs affects the aggregation degree of the NPs and, consequently, the thermal conductivity. The isoelectric point of the value of pH occurs when the amount of positive and negative ions is the same. Some studies reported an increasing enhancement of the thermal conductivity with increasing pH until the isoelectric point, which is then followed by a decrease. This was attributed to the increase of electrical charge on the surface of the NPs, leading to greater electrostatic repulsion ^[5][26]. Krishnakumar et al. ^[57] and Li et al. ^[58] reported an increase in thermal conductivity with pH of ethanol-based alumina NFs until a maximum value with pH value near 6.0, which is then followed by a decrease with increasing pH. Wang et al. ^[59] registered similar results with water-based copper and alumina NF, being the maximum thermal conductivity value obtained when the isoelectric point was reached. Other studies showed lower values of thermal conductivity in the isoelectric point, i.e., the repulsive forces among particles are zero, making particles aggregate under this pH value ^[60]. The experimental work developed by ^[61] also shown that the pH influences the zeta potential, particle size distribution, rheology, viscosity, and stability, and all these factors affect the thermal conductivity of the NFs containing ZrO

The pH of the NFs affects the aggregation degree of the NPs and, consequently, the thermal conductivity. The isoelectric point of the value of pH occurs when the amount of positive and negative ions is the same. Some studies reported an increasing enhancement of the thermal conductivity with increasing pH until the isoelectric point, which is then followed by a decrease. This was attributed to the increase of electrical charge on the surface of the NPs, leading to greater electrostatic repulsion [5,26]. Krishnakumar et al. [57] and Li et al. [58] reported an increase in thermal conductivity with pH of ethanol-based alumina NFs until a maximum value with pH value near 6.0, which is then followed by a decrease with increasing pH. Wang et al. [59] registered similar results with water-based copper and alumina NF, being the maximum thermal conductivity value obtained when the isoelectric point was reached. Other studies showed lower values of thermal conductivity in the isoelectric point, i.e., the repulsive forces among particles are zero, making particles aggregate under this pH value [60]. The experimental work developed by [61] also shown that the pH influences the zeta potential, particle size distribution, rheology, viscosity, and stability, and all these factors affect the thermal conductivity of the NFs containing ZrO

₂

and TiO

₂

NPs.

3.3.4. Additives, Surfactants and Solvents

The incorporation of additives on the NFs can help to improve the stability of the fluid over time. Wang et al. ^[27] and Zhu et al. ^[62] identified the optimal concentration of the surfactant SDBS (Sodium dodecylbenzenesulfonate) to increase the thermal conductivity of water-based copper and alumina NFs. Eastman et al. ^[63] improved the thermal conductivity of ethylene glycol-based copper NFs by adding thioglycolic acid. High concentrations of additives can lead to negative effects on the NFs, such as flocculation. When adding reduced amounts of additive little or no effect on the thermal conductivity was reported ^[13][26]. The experimental work developed by ^[64] demonstrated the impact on the alignment and dispersion of the NPS and on the thermal conductivity of the NFs that the surfactants and solvents may have. In this study, the authors measured the thermal conductivity of Fe

The incorporation of additives on the NFs can help to improve the stability of the fluid over time. Wang et al. [27] and Zhu et al. [62] identified the optimal concentration of the surfactant SDBS (Sodium dodecylbenzenesulfonate) to increase the thermal conductivity of water-based copper and alumina NFs. Eastman et al. [63] improved the thermal conductivity of ethylene glycol-based copper NFs by adding thioglycolic acid. High concentrations of additives can lead to negative effects on the NFs, such as flocculation. When adding reduced amounts of additive little or no effect on the thermal conductivity was reported [13,26]. The experimental work developed by [64] demonstrated the impact on the alignment and dispersion of the NPS and on the thermal conductivity of the NFs that the surfactants and solvents may have. In this study, the authors measured the thermal conductivity of Fe

₂

O

₃

and CuO NPs dispersing in water, ethylene glycol, and water with SDBS as a surfactant.

3.3.5. Sonication Time

The sonication treatment is very common when preparing NFs. For most fluids, the increase of the sonication time contributes to an increase of the thermal conductivity since sedimentation is mitigated and the Brownian motion as well as the particle uniformity improved. Nevertheless, if the sonication time is too long, aggregation decreases and so is the thermal conductivity ^[5][26]. Hong et al. ^[65] reported increasing values of thermal conductivity with increasing sonication time until 50 min for ethylene glycol-based iron NFs. Higher sonication values corresponded to a decrease in thermal conductivity. Also, excessive sonication can break NPs with high aspect ratio such as nanotubes ^[66] and disrupt the effect of the addition of dispersants to the NFs ^[67].

The sonication treatment is very common when preparing NFs. For most fluids, the increase of the sonication time contributes to an increase of the thermal conductivity since sedimentation is mitigated and the Brownian motion as well as the particle uniformity improved. Nevertheless, if the sonication time is too long, aggregation decreases and so is the thermal conductivity [5,26]. Hong et al. [65] reported increasing values of thermal conductivity with increasing sonication time until 50 min for ethylene glycol-based iron NFs. Higher sonication values corresponded to a decrease in thermal conductivity. Also, excessive sonication can break NPs with high aspect ratio such as nanotubes [66] and disrupt the effect of the addition of dispersants to the NFs [67].

3.3.6. External Magnetic Field

The NFs can incorporate several magnetically sensitive metal or metal oxide NPs. In such cases, the magnetic particles can have a diversity of configurations depending on the nature of the particles and on the magnetic field magnitude or strength. If the field is strong enough, the small-dimensioned particle will form connected networks or chains that tend to get oriented toward the magnetic field direction. This alignment effect will move the particles nearby and promotes a larger number of physical contacts and interaction between each other and, thus, resulting in enhanced thermal conductivity and heat transfer capability of the NF. This can be observed in the experimental works performed with Fe

₂

O

₃ or Ni and carbon Nanotubes ^[68][69]. Also, these studies have demonstrated that as the magnitude of the applied magnet field decreases, the time to reach the maximum peak value of the thermal conductivity will increase.

or Ni and carbon Nanotubes [68,69]. Also, these studies have demonstrated that as the magnitude of the applied magnet field decreases, the time to reach the maximum peak value of the thermal conductivity will increase.

3.3.7. Aggregation

In recent years, the introduction of carbon nanotubes in NFs has promoted significant research efforts due to their promising enhanced thermal conductivity and, consequently, applications in the cooling and lubricants fields. However, NFs with only a suspension of stand-alone nanotubes do not often exhibit substantially improved thermal conductivity levels. This is likely due to the infrequent physical contacts of the nanotube between each other, as they assume irregular positioning and distribution in the base fluid. To overcome this problem in practice, there are two available ways. One is to increase the volume fraction of the nanotube on the base fluid, which may lead to excessive viscosity of the NF. The other way can be found in the work developed by [70], where the authors proved that the aggregation of oppositely charged NPS (metal oxide and nanotubes) into combined clusters can explain the overall thermal conductivity enhancement. With the proper control of conditions of the suspension itself, it is possible to add fractions of positively charged metal oxide particles on the base fluid that will aggregate on the negatively charged nanotube surface (which is a phenomenon that can be enhanced with the addition of a surfactant) and hence form the aggregation cluster chain along the nanotube by electrostatic attraction.

4. Controversies in Thermal Conductivity Measurements

A large variety of techniques and devices to measure the thermal conductivity of NFs can be commonly found in the literature. Although some of the devices may be more sophisticated than others, they all converge on a common problem: they are very sensitive and dependent on the initial conditions of the samples. Even for minimal variations, the results can promote a strong impact on the final conclusions. Most of the techniques presented in this work have been adapted over the years to be able to safely measure the thermal conductivity of NFs. This task has not been easy due to the difficulty of maintaining the stability of the samples. The dispersion techniques proposed by recent research studies ^[71] can achieve months of stability, but the recurring necessity of continuous maintenance and the gradual sedimentation of the nanoparticles throughout the system can help us understand the reason for so many controversial results.

A large variety of techniques and devices to measure the thermal conductivity of NFs can be commonly found in the literature. Although some of the devices may be more sophisticated than others, they all converge on a common problem: they are very sensitive and dependent on the initial conditions of the samples. Even for minimal variations, the results can promote a strong impact on the final conclusions. Most of the techniques presented in this work have been adapted over the years to be able to safely measure the thermal conductivity of NFs. This task has not been easy due to the difficulty of maintaining the stability of the samples. The dispersion techniques proposed by recent research studies [100] can achieve months of stability, but the recurring necessity of continuous maintenance and the gradual sedimentation of the nanoparticles throughout the system can help us understand the reason for so many controversial results. Another reported difficulty is associated with the concentration of the NPs in the BF. Even though the results have not yet reached a general consensus, the simplest solution found by the majority of the researchers to increase the gains in thermal conductivity of colloidal mixtures is to increase the concentration of NPs in the BF. However, as the concentration of the NPs increases, NF viscosity also increases, leading to flow resistance. The greater viscosity of those fluids increases power requirements of the pumping system and pressure losses in the case of heat sinks, when compared to the respective base fluids.

Another property that can affect the measurement of the thermal conductivity of NFs is the specific heat of all their components, that is, the BFs, NPs and dispersants used. This property relevance and its effects are also not unanimous among the scientific community and are not yet fully understood. The high specific heat of water is the main reason why it is used as cooling fluid in a large variety of applications, even when compared to other fluids. In this way, it is possible to provide a high amount of energy, without promoting a high increase of temperature at the systems. On the other hand, the NPs used to form the colloidal mixtures have a lower specific heat, and this lower contribution of the NPs to the NF heat capacity needs to be compensated. For example, Nieh et al. ^[72], using an NF formed by NPs ofAl

Another property that can affect the measurement of the thermal conductivity of NFs is the specific heat of all their components, that is, the BFs, NPs and dispersants used. This property relevance and its effects are also not unanimous among the scientific community and are not yet fully understood. The high specific heat of water is the main reason why it is used as cooling fluid in a large variety of applications, even when compared to other fluids. In this way, it is possible to provide a high amount of energy, without promoting a high increase of temperature at the systems. On the other hand, the NPs used to form the colloidal mixtures have a lower specific heat, and this lower contribution of the NPs to the NF heat capacity needs to be compensated. For example, Nieh et al. [101], using an NF formed by NPs ofAl

₂

O

₃

or TiO

₂

prepared with ethylene glycol/water, studied the effect of adding a dispersant to evaluate the influence in the specific heat. They observed an increase of the specific heat but, it was gradually decreased with the increase of wt% of Al

₂

O

₃

and TiO

₂. Without addition of the dispersants, some researchers have shown that the specific heat of NFs decreases with the increase of volume fraction ^[72][73][74].

. Without addition of the dispersants, some researchers have shown that the specific heat of NFs decreases with the increase of volume fraction [101,102,103]. The potential of NFs to increase the heat transfer capacity of thermal systems is accepted by a large part of the scientific community. However, the lack of consistent results obtained by different researchers has hampered the development of this field and the use of NFs in large scale industrial applications. The poor characterization of the suspensions of NPs and the lack of theoretical understanding of the mechanisms responsible for thermal properties changes need further understanding. Many issues besides the thermal conductivity, such as the Brownian motion and sedimentation of NPs, particle migration, and temperature-dependent properties, must be carefully considered, especially when the thermal analysis involve not only natural but also convective heat transfer phenomena within the nanofluid.

5. Backdraws and Future

The backdraws, difficulties and general limitations of the NFs can be summarized in the following points:

• Methods to scale-up production for commercialization are still in development;
• Some of the classical experimental fitting prediction models for thermal properties are not the most suitable for the estimation of the thermal conductivity, dynamic viscosity and density of the NFs;

By way of guidelines that might be the path for future challenges and further studies and developments, the authors of the current work wish to emphasize the following:

• The stability and durability of the nanofluids should be improved by optimizing the concentration of NPs and base fluid characteristics (e.g., chemical, viscosity). The stability of nanofluids should also be predicted by further analysis of the surface tension of the nanofluid vs. time;
• The general properties of the NFs should be improved by optimizing the preparation procedures (e.g., sonication time);
• The influence of the solvents should be further studied: the use of high polar solvents like the DMF (Dimethylformamide) and THF (Tetrahydrofuran) and non-polar solvents as hexane and heptane could be the right way to fully understand how polarity influences the alignment and thermal conductivity of the NFs;
• The influence of the polarity in the alignment of the NPS on the base fluid can also be assessed by the use of different surfactants with negative charge, such as for instance CATB (Cetyltrimethylamonium bromide);
• The classical modeling does not provide a fast prediction of the thermal properties, which may slow down the study and overall applicability of the NFs;
• The impact of an applied magnetic field should be further studied, namely the value or range of values that make possible to reach the thermal conductivity maximum peak in less time;
  Nowadays, it is clear the need to use the recent statistical data-driven machine learning models to obtain faster predictions of the thermal properties of the NFs. Those models are also more stable and sensitive than the empirical ones. However, for a in-depth knowledge on how the recent models work, the researchers must get proficient skills in machine learning methodology and in the most common data-driven models and algorithms;
• The proper machine learning model and algorithms should be chosen according to the dimension of the sample, the available computing resources, and the required prediction performance (modeling stability and sensibility).
• viscosity of NFs increases with the concentration of the NPs leading to higher pumping power requirements;
  Additives for decreasing the NFs viscosity while maintaining the same level of thermal conductivity are of paramount importance to achieve the best performance of the NFs;
• NF long-term stability is mandatory for miniaturized fluidic systems, mainly mini or microchannels devices;
  The systems using nanofluids as working fluid should become more cost-effective, without the need of extra pumping power and expensive maintenance. This should be accomplished with the optimization of the microchannels configuration (e.g. number of channels, inlet/outlet positioning);
• the production costs for systems using nanofluids as working fluid are still high.
  Machine learning prediction models should be increasingly used in the future, since they provide faster and less expensive modeling of thermal properties of the NFs. Those data-driven models achieve more accurate and stable estimations than the classical ones. The path created by machine learning is beginning to clear up several doubts and backdraws, and it is a secure one for future studies and developments on the nanomaterials field of research.

• Complexity and high cost of NFs preparation;
• Nowadays, it is clear the need to use the recent statistical data-driven machine learning models to obtain faster predictions of the thermal properties of the NFs. Those models are also more stable and sensitive than the empirical ones. However, for a in-depth knowledge on how the recent models work, the researchers must get proficient skills in machine learning methodology and in the most common data-driven models and algorithms;
• The proper machine learning model and algorithms should be chosen according to the dimension of the sample, the available computing resources, and the required prediction performance (modeling stability and sensibility).

• Complexity and high cost of NFs preparation;
• Long-term stable NFs are difficult to produce. The influence of the production should be further studied, namely the sonication time, volume fraction, and type of the NFS in order to avoid the sedimentation and agglomeration of the NPs in the BF and to achieve optimal performance;
• Lack of a common protocol for the manufacture and analysis of the thermal transport mechanisms in this type of fluids;

6. Conclusions

From all the results and discussions shown in this literature review, it is clear that the benefits of nanofluids are vast, since they can be used in a wide variety of applications from nanomedicine to renewable energies. Due to their superior thermal properties, nanofluids have become protagonists in increasing the heat transfer from the thermal systems as their use very suitable to miniaturize fluidic systems. Although the series of studies presented by the scientific community are not always consistent, several results generally converge on the same conclusions, as follows:

• the thermal conductivity of an NF is greater than the one of the respective base fluids;
• the methods used to measure the thermal properties of NFs are still in an embryonic stage of development;
• the heat transfer coefficient of an NF is higher than the one of the respective base fluid;

• Long-term stable NFs are difficult to produce. The influence of the production should be further studied, namely the sonication time, volume fraction, and type of the NFS in order to avoid the sedimentation and agglomeration of the NPs in the BF and to achieve optimal performance;

• Lack of a common protocol for the manufacture and analysis of the thermal transport mechanisms in this type of fluids;
• Methods to scale-up production for commercialization are still in development;
• Some of the classical experimental fitting prediction models for thermal properties are not the most suitable for the estimation of the thermal conductivity, dynamic viscosity and density of the NFs;
• The classical modeling does not provide a fast prediction of the thermal properties, which may slow down the study and overall applicability of the NFs;