Alternating Current Loss of Superconductors: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Rita Xu and Version 1 by Hongye Zhang.

Superconductor technology has attracted increasing attention in power-generation- and electrical-propulsion-related domains, as it provides a solution to the limited power density seen by electrical machines. Superconducting machines, characterized by both high power density and high efficiency, can effectively reduce the size and mass compared to conventional machine designs. This opens the way to large-scale purely electrical applications, e.g., all-electrical aircraft. The alternating current (AC) loss of superconductors caused by time-varying transport currents or magnetic fields (or both) has impaired the efficiency and reliability of superconducting machines, bringing severe challenges to the cryogenic systems, too. Therefore, it is of significance to clarify the AC loss characteristics in superconducting machines. This entry serves to demonstrate the state of the art in this research area, provide a useful reference for the design of superconducting machines, and deliver a helpful guideline for future research efforts. 

  • alternating current loss
  • superconducting machine
  • low/high-temperature superconductor
  • superconducting coil
  • trapped field magnet

1. Introduction

Electrical machines are the key component of the power industry and have been extensively employed in power generation, transportation, defense, industrial electrical automation, as well as household appliances, etc. [1,2][1][2]. Electrical generators produce virtually all artificial electrical energy on Earth, and electric motors are responsible for approximately 40% of overall power consumption all over the world [3]. With the progress of worldwide industrialization and urbanization, the electricity demand is increasing rapidly, which has brought a negative impact on the global environment, due to the consumption of natural resources such as fossil fuels [4]. Therefore, the electromechanical energy conversion efficiency and energy utilization efficiency of electrical machines are crucial to green energy and sustainable energy strategies. However, despite many attempts to improve the efficiency and power density of conventional machines [5[5][6][7][8],6,7,8], their incremental advances have not brought about a fundamental qualitative change. For instance, although the existing electrical machine technologies have satisfied the development of electric vehicles [9[9][10],10], they cannot achieve the step change in power density required for electric aircraft and marine transport [11]. In wind turbines, the use of direct drive eliminates the need for a mechanical gearbox, but the low speed high torques encountered in renewable energy converters results in a very large-diameter machine with high mass [12,13][12][13]. Both transport and energy sectors are experiencing an electrical revolution in the transition to net zero emissions, but the limited power density of traditional electrical machines requires radical progress. Superconducting machines, characterized by high efficiency and power density, open the way to zero-emission transport and power systems [14,15][14][15].

The majority of superconducting machine designs are based on conventional topologies, in which the field or armature windings (or both) are built with superconducting coils or replaced by trapped field magnets (TFMs) [11,12,13,14,15][11][12][13][14][15]. A summary of superconducting materials adopted for superconducting coils and TFMs will be presented in Section 2. AC loss is generated by the movement of magnetic vortices within the superconductor when experiencing time-varying currents or magnetic fields [16]. Inside electric machines, the electromagnetic environment is complicated, composed of abundant AC electromagnetic signals and high-frequency harmonics, especially for high-speed rotating machines. As a result, AC loss of superconductors becomes a key challenge for machine designs, in that not only does it affect the construction of cryocoolers and impair the efficiency of the system, but it also causes security hazards in case of quench (for superconducting coils) or demagnetization (for TFMs). The main concern regarding AC loss comes from armature windings [17]. To avoid high AC loss, a number of researchers have adopted partially superconducting machines, i.e., superconductors are only used as field sources by means of direct current (DC) carrying coils or TFMs, and armature windings are made of conventional conductors [18,19][18][19]. However, it appears difficult for partially superconducting machines to achieve a power density higher than 20 kW/kg required for future aviation [11]. Nowadays, targeted at high power superconducting machines for aircraft and aerospace applications, more and more researchers begin to focus on fully superconducting machines. As a result, AC loss of superconductors becomes inevitably one of the most challenging issues to be solved.

Figure 1 shows the AC loss per unit length of an example 12-mm-wide high-temperature superconductor (HTS) coated conductor (CC) and its filamentized tapes exposed to an externally applied AC magnetic field with an amplitude varying from 1 to 100 mT, at 40 Hz [20]. It can be seen that the AC loss of the HTS CC increases positively with the applied magnetic field, and for a CC without filaments, the power dissipation per unit length can attain 1 W/m even under a field as low as 20 mT at a low frequency of 40 Hz. The power is dissipated at cryogenic temperature, e.g., at liquid nitrogen temperature 77 K, which can constitute a big cryogenic burden. Table 1 presents the estimated heat load of HTS motors and generators employing different HTS materials at the operating temperature. To remove the heat load contributed by the AC loss, high cooling power is expected. Table 2 shows the ideal and practical Carnot specific power at a working temperature varying from 4.2 to 273 K. Carnot specific power is the quantity of watts needed at ambient temperature to offer 1 W of refrigeration at the lower working temperature [21]. At present, commercially available refrigerators function far below the Carnot efficiency, i.e., their practical Carnot specific power is much higher than the ideal one, as shown in Table 2. According to Figure 1 and Table 1 and Table 2, it is not difficult to conclude that the heat load due to the AC loss of HTS materials applied to electrical machines proposes a big challenge for the design of cryogenic systems.

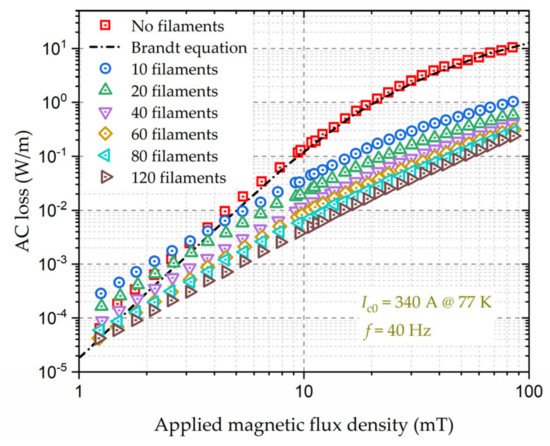
Energies 14 02234 g001 550

Figure 1. Variation of the AC loss of a 12-mm-wide YBCO CC and its filamentized tapes with externally applied AC magnetic fields. The self-field critical current, Ic0, of the YBCO CC is 340 A at 77 K, and the frequency, f, of the AC magnetic field is 40 Hz. Experimental data are from [20].

Table 1.

Estimated heat load of HTS machines at the working temperature [21].

HTS Machines Power Level BSCCO Heat Load YBCO Heat Load
Working Temperature (K) Ideal Carnot Specific Power (W) Practical Carnot Specific Power (W) (When Heat Load > 100 W)
Generators 10–500 MW 100–500 W at 25–40 K 100–500 W at 50–65 K
Motors
273 0.11 0.4
1–10 MW 50–200 W at 25–40 K 50–200 W at 50–65 K

Table 2.

Ideal and practical Carnot specific power at distinct working temperatures [21].

77 2.94 12–20
50 5.06 25–35
20 14.15 100–200
4.2 71.14 11,000

The AC loss of superconductors has been widely studied by many researchers; however, we have not seen a systematic review to summarize the advancements with respect to AC loss analysis during the last dozen years, especially combined with superconducting machines. Aiming to illuminate the state of the art of AC-loss-related research work and determine its future research trends in superconducting machine domains, we have conducted a comprehensive overview of AC-loss-related topics, including superconducting materials adopted in electrical machines, loss mechanism, and analytical formulae, modelling methods, measurement approaches, as well as loss reduction techniques. It should be pointed out that, as reported by our previous research work [22,23,24][22][23][24], the superconductors employed in high-speed rotating machines have to experience high-frequency electromagnetic environments. In this case, the total loss inside electrical machines is not purely contributed by the superconducting parts, but also by the normal conducting parts, due to the skin effect, which poses great challenges to the existing loss quantification and reduction techniques. Therefore, AC loss at high frequencies will be highlighted and discussed throughout the paper. This review work is believed to help researchers better understand the research status of AC loss in superconductors and to provide a useful reference for superconducting machine designs, especially for those functioning at high speeds for future aviation.

2. Superconducting Materials Applied to Electrical Machines

Superconducting materials can be categorized into low-temperature superconductors (LTSs), e.g., NbTi, and HTSs, e.g., REBCO (rare-earth barium copper oxide), and BSCCO (bismuth strontium calcium copper oxide), according to their critical temperature. For LTSs, their critical temperature is normally below 30 K. The unit cost, critical temperature, and current-carrying capacity of different materials are presented in Table 3. As for superconducting coils, nowadays most researchers in the applied superconductivity community concentrate on HTS CC-based coils because they can operate in liquid nitrogen (LN2) with a higher critical temperature in addition to a higher critical current and critical magnetic field. Certainly, HTS has a better current-carrying capacity if they operate at lower temperatures. The cost of commercial HTS materials, e.g., ~69 USD/m for a 12-mm-wide YBCO tape [25], is a primary factor limiting the development of HTS machines. With the advancement of processing techniques and material science, HTS materials are expected to have a lower cost in the near future. LTSs, in spite of having a worse current-carrying capacity compared to HTSs, have still been used in several designs because of their relatively lower material cost. However, they have to operate at liquid helium (LHe) or liquid hydrogen (LH2) temperature; thus, the cryogenic systems of LTS machines are generally more complicated and costly [26,27][26][27]. Concerning AC loss, MgB2 possesses the advantage of a round wire compared with a flat tape; thus, it has the potential to become a low AC loss superconductor operating below 30 K [28]. Given this fact, many fully superconducting machine designs have adopted MgB2 coils as armature windings to avoid unbearable AC loss [29,30,31][29][30][31]. To maintain high electrical and magnetic loadings, while decreasing AC loss, multifilamentary HTS CCs have been implemented into electrical machines as an alternative [32]. The typical structure and composites of different superconductors can be found in Figure 2.

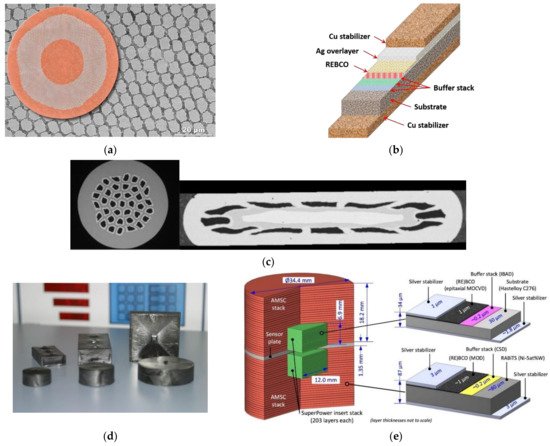
Energies 14 02234 g002 550

Figure 2. Diagrams of the superconductors applied to electrical machines: (a) Cross section of a NbTi wire (LTS). Illustration courtesy of Peter J. Lee, NHMFL; (b) Multilayer structure of an REBCO coated conductor (HTS); (c) Cross sections of round and flat MgB2 wires. Image courtesy of G. Grasso (© ASG Superconductors); (d) Photo of REBCO bulk superconductors, © evico GmbH; (e) Diagram of a trapped field HTS stack. Adapted from [45][33].

Table 3. Reported commercial superconductor specifications. Data are from [33,34,35,36,37,38,39,40,41,42,43,44][34][35][36][37][38][39][40][41][42][43][44][45].

Material Unit Cost Tc Ic0
REBCO (12 mm-width) ~227 $/(kA·m) up to 119 K 400–600 A (SuperPower, 77 K)
REBCO (4 mm-width) ~230 $/(kA·m) up to 119 K >100 A (SuperOX, 77 K)

min. 88-min. 152 A (SuperPower, 77 K)

min. 130 A (AMSC, enhanced pinning, 77 K)

>165 A (Fujikura, 77 K)

>150 A (SuNAM, 77 K)

~150 A (Shanghai SC, 77 K)

>100 A (SWCC, 77 K)
Bi-2223 17.4 $/(kA·m) 110 K ~170–~200 A (SEI, 77 K)
NbTi (LTS) 0.8 $/(kA·m) 9.5 K Up to 3 kA (SuperCon, 4.2 K)
MgB2 20 $/(kA·m) 39 K ~157 A (MgB2/Ga(30), 4.2 K)
NdFeB (PM) 28.9 $/kg / /
Copper 11.6 $/kg / /
Iron (Silicon steel) 1.6 $/kg / /

Tc critical temperature; Ic0—critical current in the self-field; PM—permanent magnet

TFMs consist of bulk superconductors and TFSs, most of which are manufactured by REBCO, despite the existence of MgB2 bulks. TFMs can give a magnetic field up to a significant degree higher contrasted with conventional PMs. Besides, different from electromagnets such as coils, no connection to a power supply is needed for TFMs. In 2014, Durrell et al. reported a trapped field of 17.6 T at 29 K in a stack of two silver doped GdBCO superconducting bulk samples [46]. A record-high trapped field of 16.1 T in MgB2 bulk has been recently achieved at 20 K by Hirano et al. using pulsed-field magnetization (PFM) [47]. The possibility of the application of bulk superconductors to electrical machines has been discussed by many researchers. Kurbatova et al. have presented an electromagnetic analysis of an electrical generator equipped with HTS bulks on the rotor and revealed that the generator performance depends on the HTS properties and the parameters of the magnetization [48]. Izumi et al. have developed an axial-gap-type synchronous machine utilizing GdBCO bulks as field poles, which is meant for low-speed ship propulsion [49]. Bulk superconductors can also serve as lightweight and compact magnetic shields in electrical machines, as reported by Leveque et al. [50]. However, a pivotal disadvantage of bulk superconductors lies in their thermal instability at low temperatures, making it hard to exploit the high critical current under 30 K [51]. In addition, external mechanical support is required in the utilization of bulk superconductors on account of their restricted mechanical strength. Compared with bulk superconductors, TFSs have better thermal stability and mechanical strength on the grounds that the copper stabilizers and silver overlayer of REBCO CCs have a thermal conductivity over a significant degree higher than REBCO, and the Hastelloy substrate has a more grounded tensile strength contrasted with REBCO. A trapped field of 17.7 T at 8 K in a stack of HTS tapes was reported by Patel et al. in 2018 [33][34]. The application of TFSs as field poles to a 1 MW superconducting demonstrator motor is being explored in the EU project ASuMED [14]. As mentioned in [52], in terms of the energization method, TFMs can avoid the application of current leads during operation compared to DC superconducting coils. However, the maximum size of TFMs can be limited by the existing production technology, especially for TFSs, and they can experience a possible demagnetization under cross fields [53], bringing a threat to the safe operations of superconducting electrical machines.

References

  1. Lei, G.; Zhu, J.; Guo, Y.; Liu, C.; Ma, B. A Review of Design Optimization Methods for Electrical Machines. Energies 2017, 10, 1962.
  2. Wildi, T. Electrical Machines Drives and Power Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 2005.
  3. Saidur, R. A review on electrical motors energy use and energy savings. Renew. Sustain. Energy Rev. 2010, 14, 877–898.
  4. Hossain, M.S. Panel estimation for CO2 emissions, energy consumption, economic growth, trade openness and urbaniza-tion of newly industrialized countries. Energy Policy 2011, 39, 6991–6999.
  5. Cheng, M.; Sun, L.; Buja, G.; Song, L. Advanced Electrical Machines and Machine-Based Systems for Electric and Hybrid Vehicles. Energies 2015, 8, 9541–9564.
  6. Cheng, M.; Zhu, Y. The state of the art of wind energy conversion systems and technologies: A review. Energy Convers. Manag. 2014, 88, 332–347.
  7. Wrobel, R.; Mecrow, B.C. A Comprehensive Review of Additive Manufacturing in Construction of Electrical Machines. IEEE Trans. Energy Convers. 2020, 35, 1054–1064.
  8. Li, S.; Zhang, S.; Habetler, T.G.; Harley, R.G. Modeling, Design Optimization, and Applications of Switched Reluctance Machines—A Review. IEEE Trans. Ind. Appl. 2019, 55, 2660–2681.
  9. Lee, D.; Park, G.; Son, B.K.; Jung, H. Efficiency improvement of IPMSG in the electric power generating system of a range-extended electric vehicle. IET Electr. Power Appl. 2019, 13, 943–950.
  10. Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Analysis and Design Optimization of a Permanent Magnet Synchronous Motor for a Campus Patrol Electric Vehicle. IEEE Trans. Veh. Technol. 2019, 68, 10535–10544.
  11. Sahoo, S.; Zhao, X.; Kyprianidis, K. A Review of Concepts, Benefits, and Challenges for Future Electrical Propulsion-Based Aircraft. Aerospace 2020, 7, 44.
  12. Jlassi, I.; Cardoso, A.J.M. Fault-Tolerant Back-to-Back Converter for Direct-Drive PMSG Wind Turbines Using Direct Torque and Power Control Techniques. IEEE Trans. Power Electron. 2019, 34, 11215–11227.
  13. Taherian-Fard, E.; Sahebi, R.; Niknam, T.; Izadian, A.; Shasadeghi, M. Wind Turbine Drivetrain Technologies. IEEE Trans. Ind. Appl. 2020, 56, 1729–1741.
  14. Grilli, F.; Benkel, T.; H¨anisch, J.; Lao, M.; Reis, T.; Berberich, E.; Wolfst¨adter, S.; Schneider, C.; Miller, P.; Palmer, C.; et al. Superconducting motors for aircraft propulsion: The Advanced Superconducting Motor Experimental Demonstrator project. J. Phys. Conf. Ser. 2020, 1590, 012051.
  15. Haran, K.S.; Kalsi, S.; Arndt, T.; Karmaker, H.; Badcock, R.; Buckley, B.; Haugan, T.; Izumi, M.; Loder, D.; Bray, J.W.; et al. High power density superconducting rotating machines—development status and technology roadmap. Supercond. Sci. Technol. 2017, 30, 123002.
  16. Ainslie, M.D.; Bumby, C.W.; Jiang, Z.; Toyomoto, R.; Amemiya, N. Numerical modelling of dynamic resistance in high-temperature superconducting coated-conductor wires. Supercond. Sci. Technol. 2018, 31, 074003.
  17. Feddersen, M.; Haran, K.S.; Berg, F. AC Loss Analysis of MgB2-Based Fully Superconducting Machines. IOP Conf. Ser. Mater. Sci. Eng. 2017, 279, 012026.
  18. Fair, R.; Lewis, C.; Eugene, J.; Ingles, M. Development of an HTS hydroelectric power generator for the hirschaid power station. J. Phys. Conf. Ser. 2010, 234, 032008.
  19. Corduan, M.; Boll, M.; Bause, R.; Oomen, M.P.; Filipenko, M.; Noe, M. Topology Comparison of Superconducting AC Machines for Hybrid Electric Aircraft. IEEE Trans. Appl. Supercond. 2020, 30, 1–10.
  20. Demencik, E.; Vojenciak, M.; Kario, A.; Nast, R.; Jung, A.; Goldacker, W.; Grilli, F. AC Loss and Coupling Currents in YBCO Coated Conductors With Varying Number of Filaments. IEEE Trans. Appl. Supercond. 2014, 24, 1–8.
  21. Grilli, F.; Pardo, E.; Stenvall, A.; Nguyen, D.N.; Yuan, W.; Gomory, F. Computation of Losses in HTS Under the Action of Varying Magnetic Fields and Currents. IEEE Trans. Appl. Supercond. 2014, 24, 78–110.
  22. Zhang, H.; Yao, M.; Kails, K.; Machura, P.; Mueller, M.; Jiang, Z.; Xin, Y.; Li, Q. Modelling of electromagnetic loss in HTS coated conductors over a wide frequency band. Supercond. Sci. Technol. 2019, 33, 025004.
  23. Zhang, H.; Machura, P.; Kails, K.; Chen, H.; Mueller, M. Dynamic loss and magnetization loss of HTS coated conductors, stacks, and coils for high-speed synchronous machines. Supercond. Sci. Technol. 2020, 33, 084008.
  24. Kails, K.; Zhang, H.; Machura, P.; Mueller, M.; Li, Q. Dynamic loss of HTS field windings in rotating electric machines. Supercond. Sci. Technol. 2020, 33, 045014.
  25. Miura, S.; Iwakuma, M.; Izumi, T. Lightweight Design of Tens-MW Fully-Superconducting Wind Turbine Generators With High-Performance REBa 2 Cu 3 O y Wires. IEEE Trans. Appl. Supercond. 2020, 30, 9028170.
  26. Stautner, W. Cryocoolers for Superconducting Generators. In Thermal Properties of Solids at Room and Cryogenic Temperatures; Metzler, J.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 121–154.
  27. Sun, J.; Neumann, H.; Sanz, S.; Sarmiento, G.; Tropeano, M.; Marino, I.; Pujana, A.; Merino, J.M. Design and Construction of the Cryogenic Cooling System for the Rotating Magnetic Validator of the 10 MW SUPRAPOWER Offshore Superconducting Wind Turbine. IEEE Trans. Appl. Supercond. 2018, 28, 1–5.
  28. Tomsic, M.; Rindfleisch, M.; Yue, J.; McFadden, K.; Phillips, J.; Sumption, M.D.; Bhatia, M.; Bohnenstiehl, S.; Collings, E.W. Overview of MgB2Superconductor Applications. Int. J. Appl. Ceram. Technol. 2007, 4, 250–259.
  29. Nam, G.-D.; Sung, H.-J.; Go, B.-S.; Park, M.; Yu, I.-K. Design and Comparative Analysis of MgB2 and YBCO Wire-Based-Superconducting Wind Power Generators. IEEE Trans. Appl. Supercond. 2018, 28, 1–5.
  30. Lin, F.; Qu, R.; Li, D.; Cheng, Y.; Sun, J. Electromagnetic Design of 13.2 MW Fully Superconducting Machine. IEEE Trans. Appl. Supercond. 2018, 28, 1–5.
  31. Song, X.; Mijatovic, N.; Jensen, B.B.; Holboll, J. Design Study of Fully Superconducting Wind Turbine Generators. IEEE Trans. Appl. Supercond. 2015, 25, 1–5.
  32. Saruwatari, M.; Yun, K.; Iwakuma, M.; Tamura, K.; Hase, Y.; Sasamori, Y.; Izumi, T. Design Study of 15-MW Fully Superconducting Generators for Offshore Wind Turbine. IEEE Trans. Appl. Supercond. 2016, 26, 1–5.
  33. Patel, A.; Baskys, A.; Mitchell-Williams, T.B.; McCaul, A.; Coniglio, W.; Haenisch, J.; Lao, M.L.; A Glowacki, B. A trapped field of 17.7 T in a stack of high temperature superconducting tape. Supercond. Sci. Technol. 2018, 31, 09LT01.
  34. Gomory, F.; Souc, J.; Pardo, E.; Seiler, E.; Soloviov, M.; Frolek, L.; Skarba, M.; Konopka, P.; Pekarčíková, M.; Janovec, J. AC Loss in Pancake Coil Made From 12 mm Wide REBCO Tape. IEEE Trans. Appl. Supercond. 2013, 23, 5900406.
  35. Hayashi, K. Commercialization of Bi-2223 Superconducting Wires and Their Applications. Sei Tech. Rev. 2020, 91, 68–74. Available online: (accessed on 10 January 2021).
  36. Ku, M.-H.; Kang, M.-H.; Lee, H.-J.; Cha, G.-S. The Critical Current Characteristics and n-value Measurement of HTS Tapes. Pro-gress Supercond. Cryog. 2010, 12, 12–16.
  37. Ishmael, S.A.; Rogers, S.; Hunte, F.; Naderi, G.; Roach, C.; Straka, W.; Schwartz, J. Current Density and Quench Behavior of MgB 2/Ga Composite Wires. IEEE Trans. Appl. Supercond. 2015, 25, 1–8.
  38. Park, M. Realization of a Large-Scale Superconducting Generator for a Wind Power Generation System; ESAS Summer School on HTS Technology for Sustainable Energy and Transport System. Available online: (accessed on 20 December 2020).
  39. Haught, D. Recent HTS activities in the US. In Proceedings of the IEA HTS Executive Committee Meeting, Milan, Italy, 19 June 2014; pp. 1–47. Available online: (accessed on 20 December 2020).
  40. Yagai, T.; Mizuno, S.; Okubo, T.; Mizuochi, S.; Kamibayashi, M.; Jimbo, M.; Takao, T.; Hirano, N.; Makida, Y.; Shintomi, T.; et al. Development of design for large scale conductors and coils using MgB2 for superconducting magnetic energy storage device. Cryogenics 2018, 96, 75–82.
  41. Elsherif, M.; Taylor, P.; Blake, S. Investigating the potential impact of superconducting distribution networks. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; p. 816.
  42. Rammah, Y.; Salama, A.; Elkhatib, M. Magnetic Moment and its Correlation with the Critical Temperature in YBCO. Int. Ceram. Rev. 2019, 68, 34–41.
  43. Tsuchiya, K.; Kikuchi, A.; Terashima, A.; Norimoto, K.; Uchida, M.; Tawada, M.; Masuzawa, M.; Ohuchi, N.; Wang, X.; Takao, T.; et al. Critical current measurement of commercial REBCO conductors at 4.2 K. J. Cryog. 2017, 85, 1–7.
  44. Jensen, B.B.; Mijatovic, N.; Abrahamsen, A.B. Development of superconducting wind turbine generators. J. Renew. Sustain. Energy 2013, 5, 23137.
  45. Bykovskiy, N.; Kaal, S.; Dudarev, A.; Mentink, M.; Kate, H.H.J.T. Demonstration of engineering current density exceeding 1 kA mm−2 in ultra-thin no-insulation, soldered coil windings using NbTi/Cu wires with CuNi cladding. Supercond. Sci. Technol. 2020, 33, 114001.
  46. Durrell, J.H.; Dennis, A.R.; Jaroszynski, J.; Ainslie, M.D.; Palmer, K.G.B.; Shi, Y.-H.; Campbell, A.M.; Hull, J.R.; Strasik, M.; E Hellstrom, E.; et al. A trapped field of 17.6 T in melt-processed, bulk Gd-Ba-Cu-O reinforced with shrink-fit steel. Supercond. Sci. Technol. 2014, 27, 082001.
  47. Hirano, T.; Takahashi, Y.; Namba, S.; Naito, T.; Fujishiro, H. A record-high trapped field of 1.61 T in MgB2 bulk comprised of copper plates and soft iron yoke cylinder using pulsed-field magnetization. Supercond. Sci. Technol. 2020, 33, 085002.
  48. Kurbatova, E.; Kurbatov, P.; Dergachev, P.; Molokanov, O. Electromagnetic Analysis of HTS Generator with Bulk Superconductor. In 2018 20th International Symposium on Electrical Apparatus and Technologies (SIELA); Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 1–4.
  49. Zhang, Y.; Zhou, D.; Ida, T.; Miki, M.; Izumi, M. Melt-growth bulk superconductors and application to an axial-gap-type rotating machine. Supercond. Sci. Technol. 2016, 29, 044005.
  50. Colle, A.; Lubin, T.; Ayat, S.; Gosselin, O.; Leveque, J. Analytical Model for the Magnetic Field Distribution in a Flux Modulation Superconducting Machine. IEEE Trans. Magn. 2019, 55, 1–9.
  51. Patel, A.; Filar, K.; Nizhankovskii, V.I.; Hopkins, S.C.; Glowacki, B.A. Trapped fields greater than 7 T in a 12 mm square stack of commercial high-temperature superconducting tape. Appl. Phys. Lett. 2013, 102, 102601.
  52. Patel, A.; Climente-Alarcon, V.; Baskys, A.; A Glowacki, B.; Reis, T. Design considerations for fully superconducting synchronous motors aimed at future electric aircraft. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Railway, Nottingham, UK, 7–9 November 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 1–6.
  53. Kapolka, M.; Pardo, E.; Grilli, F.; Baskys, A.; Climente-Alarcon, V.; Dadhich, A.; A Glowacki, B. Cross-field demagnetization of stacks of tapes: 3D modelling and measurements. Supercond. Sci. Technol. 2019, 33, 044019.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback