You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Multiscale Bone Damage: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Karina Chen and Version 1 by Federica Buccino.

The investigation of bone damage processes is a crucial point to understand the mechanisms of age-related bone fractures. In order to reduce their impact, early diagnosis is key. The intricate architecture of bone and the complexity of multiscale damage processes make fracture prediction an ambitious goal. 

  • age-related bone fractures
  • multiscale imaging
  • bone damage
  • computational models
  • experimental validation

1. Imaging Techniques for Multiscale Damage Assessment and Prediction

The use of imaging techniques enables researchers to understand bone damage at different hierarchical scales. It is particularly relevant in the comprehension of the implications of fracture processes in the deterioration of bone quality. This section presents an overview of the available imaging techniques (Figure 41) to visualize bone morphologies, to assess bone fractures and to predict the fracture risk from the macro-scale to the nano-scale. The macro-architecture is currently evaluated by means of common clinical images. At lower hierarchical levels, the identification of damage processes is more complex and requires higher-resolution techniques.
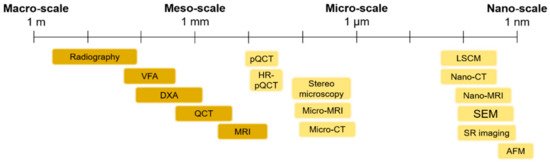
Materials 14 01240 g004 550
Figure 41. An overview of the main imaging techniques to assess bone damage at different scales. Macro- and meso-scale techniques are depicted in a darker color, while micro- and nano-scale imaging techniques are represented in a brighter color. VFA: Vertebral Fracture Assessment; QCT: Quantitative Computed Tomography; MRI: Magnetic Resonance Imaging; pQCT: peripheral Quantitative Computed Tomography; Micro-CT: Micro Computed Tomography; LSCM: Laser Scanning Confocal Microscopy; SEM: Scanning Electron Microscopy; SR imaging: Synchrotron Radiation imaging; AFM: Atomic Force Microscopy.
Different techniques are compared in terms of outcomes, in vitro or in vivo applications, resolution, two- or three-dimensional features and the main advantages and disadvantages.

1.1. Macro- and Meso-Scale Imaging

Table 1 shows the principal macro-scale techniques for the imaging of bone fractures and for fracture risk prediction.
Table 1. Overview of the main macro- and meso-scale imaging techniques.
Macro- and Meso-Scale Imaging Technique Brief Description of the Technique Invasiveness Outcomes Spatial Resolution 2D or 3D


Claustrophobia side effect
In vivo

1.2. Micro- and Nano-Scale Imaging

Table 2 shows the principal micro- and nano-scale techniques for the imaging of bone fractures and for fracture risk prediction.
Table 2. Overview of the main micro- and nano-scale imaging technique.
Micro- and Nano-Scale Imaging TechniqueAdvantages Brief Description of the Technique Invasiveness Outcomes Spatial ResolutionDisadvantages
2D or 3D Advantages Disadvantages In Vitro/In Vivo Application
In Vitro/In Vivo Application
Radiography Based on the interaction between a beam of photons (X-rays) directed from a source to a receptor. The atoms of the body prevent, in a percentage dependent on their atomic number, some photons from reaching the receptor, reproducing a “negative” image of the body No



Radiation dose: 40–50 times lower, if compared to computed tomography (CT) scans

(e.g., radiographs of the abdomen → 0.25 mGy) [39][1]		 Estimation of density variation (fracture risk prediction) by means of two indexes: Singh index [40][2] for proximal femur and cortical–medullary index [41][3] for hand radiographs 0.17 mm/pixel →

The size of the monitor screens used in digital radiography is sufficient for 35 × 43 cm2 radiographs to be displayed at a resolution of 2048 × 2560 pixels
Stereomicroscopy Based on Histological Sections Histology from the bone tissue is obtained and then the sample is properly treated (fixation, dehydration and clearing, embedding, sectioning, staining and mounting). The histological section is then observed by means of an optical microscope Yes Traditional technique for the visualization of bone microarchitecture[42][4] 2D Clear identification of distal radius fractures [43 ~1.6 µm [][5] 58][21]Difficult detection of hip and spine fractures



Insensitive to changes in Bone Mineral Density (BMD)until 20 to 40% of bone mass lost [		 2D Bone remodeling assessment [59][22]43][5]
Destructive and invasive technique



Limitations related to the bidimensional output images: the three-dimensional features are lost.

High-resolution images (at least 1.4 µm or better) are required to identify and measure individual resorption cavities in the process of bone remodeling [59][22] In vivo
Dual-energy X-ray Absorptiometry (DXA) Involves the emission of two X-ray beams with different energy levels, that collide with the body of the patient. Once the absorption of the soft tissue has been subtracted, it is possible to determine the absorption of the beam by the bone and therefore the BMD No



Low radiation dose (0.001–0.003 mGy for L-spine, to 0.004 mGy for total body) [37][6]
In vitro
Micro-Computed Tomography (Micro-CT) and Nano-Computed Tomography (Nano-CT) Micro- and nano-CT scans use radiographs to generate cross-sections of bone, that are generally processed (image reconstruction) to generate a virtual 3D model without destroying the original bone sample No



Generally, the samples are obtained from surgical wastes that derive from prosthetic treatment		Determination of areal BMD in g/cm2



Calculation of bone mineral content (BMC = BMD × area)



Calculation of T-score and Z-score (negative for values under the average BMD), that are numerical indexes for the evaluation of osteoporosis.		 Microarchitectural 3D data for both the cortical and the trabecular sections (tissue volume, bone volume, bone surface, bone volume fraction, bone surface to tissue volume, trabecular/cortical thickness, degree of anisotropy, cortical porosity, etc.) [37][6].

Local and global parameters related to the lacunar network are obtained [36		1 pixel → ≃ 0.56 × 0.56 mm2.

(for a Hologic system) [44][7]		 2D Ease of use of the equipment



Standardization



Short examination time [45][8]		 No bone architecture detection (no difference between cortical and trabecular bone)



Sampling errors



Incorrect evaluation in obese patients [37][6]
][23] 1.2 µm (micro-CT)



~50–150 nm (nano-CT)		 3D Large number of obtainable outputs (morphological parameters at different scales)



Detailed finite element 3D models could be implemented by using micro-CT images		 Static evaluation of micro-scale features



Not suitable for in vivo human evaluation due to the high radiation dose

No detection of the canalicular network (insufficient resolution for the micro-CT scans)



Nano-CT		 In vivo
In vitro Vertebral Fracture Assessment (VFA) Special DXA analysis that permits the detection of spinal fractures from a lateral image of the spine No



Lower radiation exposure with respect to spine radiography [46][9]		 Spinal fracture detection [47][10
Peripheral QCT (pQCT) and High-Resolution pQCT (HR-pQCT)] Dedicated CT scanners for the forearm (radius and ulna) and leg (tibia and fibula) No



Low radiation dose (≈0.003 mGy) [37][6]		 Analysis of the trabecular and cortical sections (BMD, bone mineral content and bone geometrical parameter calculation).

Acquisition of biomechanical parameters, such as the cross-sectional moment of inertia. Evaluation of the functional muscle–bone unit [		Low spatial resolution 60][24]. Isotropic voxel size of 82 μm with HR-pQCT2D Possibility to add a VFA scan after areal BMD assessment



High sensitivity

 3D

High specificity [48][11]		 High precision and accuracyLow spatial resolution




Low radiation dose



Applicable for the study of a large number of diseases, especially pediatric (useful in applications where trabecular and cortical sections are affected in a different way) Evaluation restricted to the appendicular bone



Only transversal data are available for fracture risk prediction



 In vivo
Low spatial resolution Quantitative Computed Tomography (QCT) X-ray-based technique that measures BMD. It produces cross-sectional images of X-ray absorption coefficient (measured in Hounsfield units) calibrated to water. It is used to evaluate fracture risk primarily at the lumbar spine and at the hip [49][12] Medium–high invasiveness



Medium–high radiation dose (0.2–0.4 mGy for a spine exam) [50][13]		 True measurement of BMD assessment

(areal BMD does not predict if an individual patient will eventually fracture)		 100× higher resolution with respect to conventional radiologic imaging [51][14[53
In vivo ]
Synchrotron Radiation Imaging (SR)3D (multiple slices are obtained and then reconstructed) A high-intensity white beam travels around a fixed closed loop. It permits a high level of detail in bone visualization (ultra-structural porosity detection)Fracture risk prediction in patients with scoliosis, obesity, etc. without having artificially high BMD values, as in DXA No

Generally, the samples are obtained from surgical wastes that derive from prosthetic treatment		[52][15] Morphological analysis of ultra-structural porosities Voxel size of 0.9 μm for the white beam [61][25]



High reproducibility



Assessment of cortical and trabecular bone

 3D

Good accuracy and precision [37][6]		 Visualization of the lacunar and canalicular network



Phase contrast permits the clear detection of micro-cracks		Relevant radiation dose



Low accessibility



High cost ][16]
Reduced field of view In vivo
In vitro Magnetic Resonance Imaging (MRI) MRIs employ a magnetic field that forces protons in the body to align with that field. When a radiofrequency current is pulsed through the patient, the protons are strained against the pull of the magnetic field. When the radiofrequency field is turned off, the MRI sensors detect the released energy as the protons realign with the magnetic field. The time it takes for the protons to realign, as well as the amount of energy released, changes depending on the environment and the chemical nature of the molecules No



MRI does not use ionizing radiation		 Bone fracture detection



Parameters: T2* [54][17] (effective transverse relaxation time) → a function of the density and orientation of the trabeculae [55][18]

R2* → rate constant of the free induction signal (lower with respect to the control in osteoporotic women’s bone marrow [		 No56][19]) MRI scanners used for medical purposes could reach typical resolutions of around 1.5 × 1.5 × 4 mm Structural parameters, such as trabecular bone thickness and mean bone volume fraction, associated with bone biomechanical properties and fracture resistance3 [57][20] Spatial resolution up to 25 µm (micro-MRI) and ~10 nm for the nano-MRI3D Useful in age-related fracture detection (marrow fat increases with age and in osteoporosis, allowing better contrast with the trabecular bone)
Micro-MRI and nano-MRI

 3D

Investigation of cortical water content [43][5] Non-destructive technique



Good special resolution



Good contrast resolution [62][26		Presence of a magnetic field (risk for patients with pacemakers and all implants containing iron)



Noise up to 120 dB



Use of contrast agents		 The technique generates images by exploiting the nuclear magnetic behavior of different atoms in a sample tissue placed in a magnetic field]

 Long acquisition times



High costs [62][26]
In vivo
Laser Scanning Confocal Microscopy (LSCM) LSCM employs lasers at proper wavelengths to excite fluorochromes that are used to stain bone sections Yes Correlation between micro-crack parameters and bone matrix toughness



Comparison among damage morphologies [13][27]		 180 nm laterally and 500 nm axially [63][28] 2D/3D

images of consecutive planes can be reconstructed into a 3D image in vitro.		 Evaluation of bone microdamage Axial resolution in depth impaired by spherical aberration [63][28]


High costs
Scanning Electon Microscopy (SEM)
SEM produces images of the bone sample by scanning the surface with a focused beam of electrons
Yes
Quantitative analysis of fracture surfaces




Visualization of microdamage morphology, fiber bridging and interlamellar separation [13][27] ~1 nm 3D

In vitro		 Significant information related to sub-micro-scale damage Destructive technique (sample surfaces should be conductive → bone needs to be coated with conductive materials)
Atomic Force Microscopy (AFM) The deflections of a cantilever on the surface of the bone sample are transduced into electrical signals Yes Topographical parameters of fractured bone surfaces (mineral particle sizes)



Identification of sacrificial bonding		 Vertical resolution → up to 0.1 nm



Lateral resolution → ~30 nm		 3D

In vitro		 Versatile imaging technique for the visualization of fracture surfaces



High accuracy



Non-destructive technique [64][29]		 Small dimensions of the single scan image size (150 × 150 µm, compared with mm for SEM)



Slow
Macro-scale in vivo images are commonly used in current clinical practice; radiologic imaging is crucial in the diagnosis of fractures, because it can detect damage or abnormalities that are not identified during physical examinations. However, this technique is insensitive to even significant changes in BMD (up to 40%, as reported in Table 1). This need for higher accuracy in bone fracture diagnosis is not completely satisfied by DXA (Table 1), which is not able to catch bone features, such as thin trabeculae, where damage presumably starts. The requirement for a higher resolution for bone damage detection is in contrast with the higher radiation dose, which should be provided when increasing the detail in bone imaging. In current clinical practice, quantitative computed tomography (QCT) is used only for well-known dangerous sites such as the hip or the lumbar spine in which the possible harm from a relevant radiation dose is far lower than the expected risk from the untreated fracture.
In recent decades, in order to find possible solutions to overcome this issue, micro- and nano-scale imaging techniques have been deeply studied with the aim to offer new tools for fracture prediction. It is interesting to point out that these in vitro techniques offer the possibility to explore micro-scale bone features and to comprehend their role in bone damage. An example is stereomicroscopy based on histological sections, that provides the possibility to assess bone damage and remodeling at a resolution higher than 2 µm, or scanning electron microscopy. However, these techniques are destructive and, in the case of stereomicroscopy, are restricted to a bidimensional analysis. The three-dimensional evaluation of bone damage at a higher resolution is crucial not only from a research perspective, but especially from the clinical point of view; the comprehension of the micro-damage physical principle and its visualization is a relevant opportunity to understand changes in the diseased tissue and to provide insights into the prevention of age-related fractures. This could be performed by the implementation of micro- and nano-scale fragility indexes, obtained with the aid of numerical models that use, as a source, micro-scale images of bone. In this context, a wide interest is devoted to micro-CT scans and synchrotron radiation (SR) images. They provide, in fact, a three-dimensional reconstruction of bone micro-architecture, which is important for the identification of microdamage, offering the optimal balance between resolution and field of view. In addition to this, the SR technique is a promising solution for the real-time visualization of bone damage, allowing the performance of mechanical tests inside the synchrotron facility. The disruptive advent of these high-resolution in vitro techniques offers the possibility to experimentally validate numerical damage models, as deeply discussed in the section “Validation approaches to multiscale damage models”. Additionally, these techniques could help the study of effective pharmacological treatments for bone pathologies. Current treatments, in fact, are administered just after an evident diagnosis of osteoporosis, often when patients have already undergone a severe fracture. Consequently, the possibility to correlate micro-scale fragility indexes with the current bone meso- and macro-architectural knowledge may support the fracture risk assessment strategies and may better address specific therapies.

2. Bone Damage Physical Principle

Imaging techniques are a valuable tool for the visualization of bone features and multiscale damage and could help in the comprehension of bone damage mechanisms. Due to the fact that bone is a hierarchical material with multiple linked scales, bone fracture mechanisms also occur at the multiscale. Those mechanisms are particularly complex and not completely understood.
At the macro-scale, there are essentially two main bone fracture modalities: impact fracture and stress fracture. The former is a fracture caused by an overload, while the latter is associated with cyclic loading and it causes material failure by excessive damage accumulation [20,65][30][31]. Stress fractures include both fatigue fractures, which result from strong physical activity, and fragility fractures, which are consequences of everyday common activities. The latter are often linked to age-related decreases in bone’s ability to self-repair. This often happens in age-related bone pathologies such as osteoporosis. At the macro-scale, the shape, size and density of bone strongly affect fracture behavior [64][29].
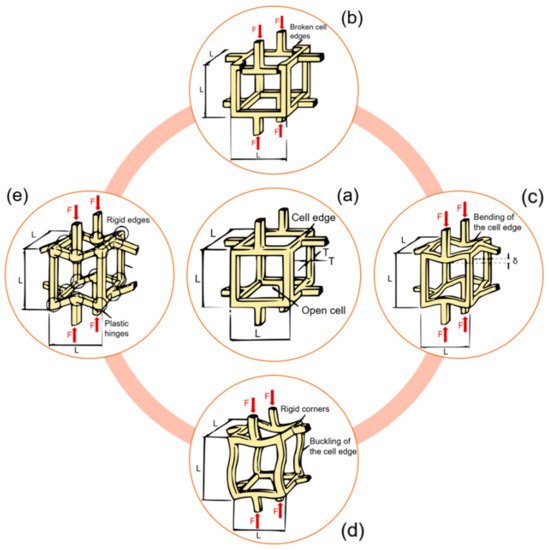
At the meso-scale, trabecular bone microarchitecture influences the damage. Trabecular bone is subjected to a variety of loads during activities of daily life and the orientation of the applied load with respect to the trabecular distribution plays an important role in a possible trabecular tissue degeneration. Indeed, trabeculae generate a three-dimensional, open porous space. Pathologies such as osteoporosis may lead to a conversion from a plate-like to a rod-like trabecular morphology, which contributes to increasing the fracture risk [66][32]. Typically, trabecular failure initiates at the weakest trabecula or at the weakest trabecular region. From there on, the failure will progress and failure bands will develop. During a tensile test, there will be only one failure band; multiple failure bands, however, occur in compressive tests [67][33]. Gibson [68][34] investigated how the basic failure modes (bending, compression, tension, shear) can explain trabecular bone failure (Figure 52). It has been also observed that complete fractures are present in trabeculae that are oriented transversally to the direction of the applied load [69][35].
Materials 14 01240 g005 550
Figure 52. Different meso-scale failure modes of a trabecular network. (a) An unloaded trabecular cell. (b) Brittle crushing. (c) Bending of horizontal rods, compression of vertical rods. (d) Buckling of vertical rods, bending of horizontal rods. (e) Plastic yielding. Readapted from [68][34].
At the micro-scale, a complete comprehension of the bone damage physical principle is still lacking. Bone is able to sustain many micro-cracks, if they are not critical; this suggests that bone can be classified as a “damage-tolerant material” [70][36]. This concept is particularly interesting when applied to bone microstructure. At the micro-scale, the damage assumes two frequent morphologies: linear and diffuse damage. The linear damage appears as a sharp line of 100–200 µm [71][37] separating the bone matrix, and it is typical of regions subjected to compression [20][30]. When external compression boundary conditions are applied, linear cracks propagate parallel to the compression loading axis [72][38]. On the contrary, diffuse damage is characterized by a cloud of tiny cracks [73][39], whose dimensions are less than 1 µm [71][37], and this is typical of regions subjected to tension. Diffuse micro-cracks are distributed transversally to the applied tensile stress [74][40]. Voide et al [75][41] suggest that diffuse damage could be considered as linear damage when oriented differently with respect to a global reference system. Micro-cracks occur on multiple planes when subjected to torsion or mixed-mode loading (Figure 63).
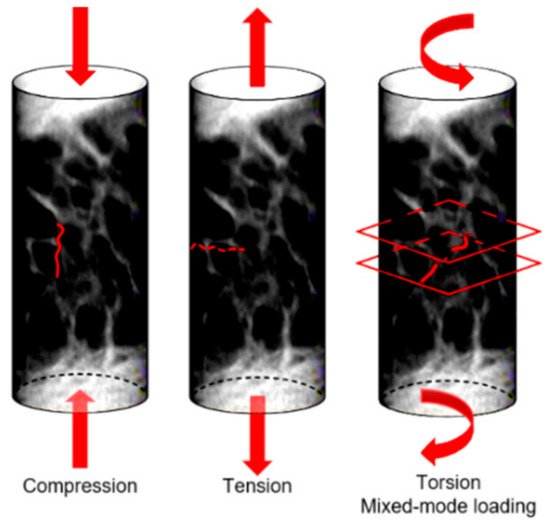Materials 14 01240 g006 550
Figure 63. Orientation of micro-cracks in a bone sample subjected to different loading conditions.
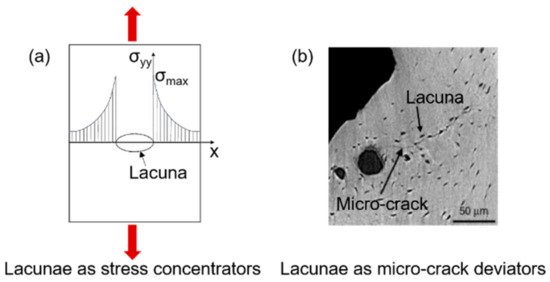
Micro-cracks usually initiate at regions characterized by high stresses. As soon as the crack initiates, its growth behavior is influenced by micro-scale heterogeneities. In this context, particular interest has recently been devoted to cellular-level porosity represented by the lacunar network, whose role is still under debate. A variation in the lacunar distribution or in the lacunar shape, as happens with aging, significantly affects the bone resistance to fracture [76][42]. Lacunae play a dual mechanical role, having an effect on both strength and toughness. In the first instance, lacunae are stress concentrators [77][43], by representing bone discontinuities able to locally amplify stresses and strains. The average strain around lacunae is 1.5–4.5 times higher than the remote strain applied to the surrounding tissue [78,79][44][45]. In this sense, lacunar system should contribute to strength decreases.
However, considering bone as a damage-tolerant material, experimental investigations [75][41] show that lacunae are not the starting point for the micro-cracks that ultimately lead to bone failure. Micro-cracks nucleate generally at canals [75][41] or at cement lines and inter-lamellar zones [80[46][47],81], where the stress amplification is greater than at the lacunae [82,83][48][49]. According to those investigations, lacunae make a beneficial contribution to toughness [72][38]. Voide et al. suggest that lacunae exert an attraction upon the existing micro-crack: the deviation of the crack path reduces the energy of its progression, slowing down crack propagation [84][50]. The two effects of the lacunar network are schematized in Figure 74. The role of the lacunar network still needs to be clarified by an effective experimental validation of the proposed hypotheses, as mentioned in Section 5.
Materials 14 01240 g007 550
Figure 74. The dual effect of the lacunar system on microdamage: lacunae as sites for crack initiation (a) and lacunae as micro-crack deviators (b); (b) is adapted from [72][38].
Finally, at the nano-scale, bone failure and fracture are influenced by bone’s composition in terms of hydroxyapatite and collagen fibers. Hydroxyapatite minerals show a brittle behavior and are more resistant to compression, while collagen fibers are more resistant to tension. When the crack propagates, the hydroxyapatite will fail first and the complete failure only occurs when collagen fibers are fully stretched [85][51].
It is understood how the comprehension of the bone damage physical principle at the multiscale level is a crucial point for the implementation of computational damage models. Those models have recently attracted a high degree of interest [86][52], due to the fact that patient-specific simulations, in particular in this context of age-related bone fractures, allow a more accurate prognosis [87,88][53][54]. The ability to quantify the effects of aging and pathologies such as osteoporosis is a challenging issue that computational damage models should consider.

3. Multiscale Computational Damage Models

Given that macro- and micro-architecture play an important role in bone damage and crack propagation, computational analyses can be interesting tools to investigate the effect of their variation due to aging on bone fractures. Using finite element (FE) models, generated directly from micro-CT or synchrotron images, it is possible to perform a “virtual experiment”, able to simulate mechanical loading of the sample and to evaluate damage formation. The main advantage of FE models is that, once the geometry of the structure is implemented, the same model can be used for multiple analyses, i.e., applying different loading conditions that may mimic everyday life loadings (e.g., walking, running).
Furthermore, bone FE models provide new insight into the relationship between damage propagation and macro- and micro-scale architecture, by allowing the localization of zones that are more prone to fracture. While in the past FE models were limited by input image resolution and computational power [87][53], nowadays, accurate simulations are feasible, thanks to the recent developments in imaging and in optimized computational software. The increased accuracy of bone FE damage models demonstrates that computational simulations are a reliable way to improve the choice of more effective experimental tests, potentially leading to a reduction in the number of performed tests [89,90][55][56].
In this section, both macro- and micro-scale models are presented, with an attempt to investigate bone fracture initiation and propagation at different scales [91][57].
Macro-scale organ-level models primarily focus on the effects of mechanical stimuli on bone resistance to fracture. Those models, that start mainly from CT reconstructions, try to implement the observation of J. Wolff [92][58], related to bone’s capability to adapt to the external mechanical loading conditions [93][59]. At this scale, micro-architectural features are neglected. The outer shape object of the problem is simplified, and filled with different meshing strategies, for instance, geometry-based with tetrahedral elements, or voxel-based with hexahedral elements. While the first method, that requires a smaller number of degrees of freedom, is not fully automated, the voxel-based hexahedron meshing has no geometrical limitations and it is a fast and completely automated mesh generation technique [94][60]. However, in the second case, outer surfaces or sharp geometrical discontinuities may generate a lack of convergence. Generally, the voxel-based meshing strategy allows a simpler and more effective interface with CT scans. The bone material is typically considered as a continuum solid [95][61]. The model is loaded with defined boundary conditions (compression, torsion or mixed-mode loading). The external load produces local stresses and strains in each considered element of the mesh (Figure 85), which could be correlated by means of the constitutive equation [96][62]. The constitutive equation, in the condition of linear elasticity, provides a linear relation between stresses and strains by means of the mechanical properties of the bone tissue, assuming the strains to be small or infinitesimal [97][63].
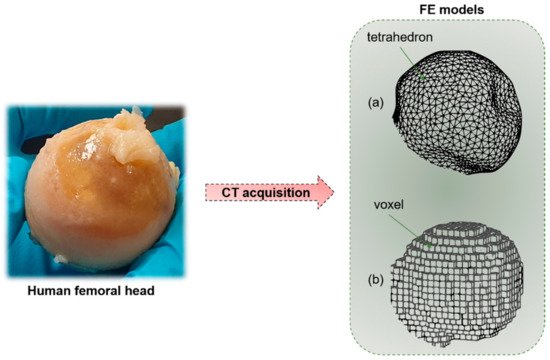Materials 14 01240 g008 550
Figure 85. Starting from a human bone (e.g., femoral head), by means of CT acquisition, it is possible to obtain a macro-scale finite element (FE) model of the sample. (a) Geometry-based FE models with tetrahedral elements. (b) Voxel-based FE model with hexahedral elements.
The initiation and propagation of damage in the macro-scale bone model is defined according to a proper failure criterion [98][64]. Based on the theory of elasticity, those models generally assume that bone resorption occurs when local mechanical stress overcomes a homeostatic stress state [99][65]. In the definition of failure at the macro-scale, it should be considered that local tissue failure could provide a loss in the structural integrity. The main results of macro-scale models, as reported in the scheme of Figure 96, show that subject-specific FE models predict values of strain with an accuracy of 90%, obtained by comparison with experimental measurements on cadaver bones (the average errors on surface strains are lower than 10%) [100][66]. The encouraging results are due to the coexistence of a precise geometric reconstruction, an appropriate choice of the density–elasticity relationship, an accurate application of boundary conditions and a suitable algorithm for material property evaluation.
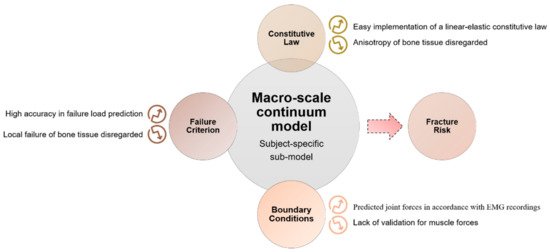Materials 14 01240 g009 550
Figure 96. Scheme for the implementation of a whole-bone model. Results, potentialities and limitations are highlighted for each step. EMG: Electromyography.
A relevant aspect of macro-scale models is that they can consider an accurate map of the tissue elastic modulus distribution, based on the density distribution over the continuum bone model, as performed by Viceconti [98][64] and Taddei [101][67]. These models show low average error in predicting failure load in vitro and have a high precision in identifying the location of failure [98][64].
Further attempts in macro-scale FE modes have been performed in order to capture the non-linear behavior of bone that depends both on the anatomic site and the loading mode. In particular, Imai et al. [102][68] observe that the prediction of vertebral fracture is intricate due to the complex geometry of the vertebra and its elastoplasticity. They implement non-linear FE models of the whole vertebra; in order to consider bone heterogeneity, the mechanical properties of each element are computed from the Hounsfield unit value. The correlation between the measured value of fracture strength and the predicted values with the non-linear FE models shows significant improvements [102][68] with respect to previous linear and simplified FE models. Other attempts in modeling bone failure have been performed by Harrison et al. [103][69], considering that the tissue failure consists of two phases: damage and fracture. This study develops a computational model consisting of an explicit representation of complete failure, incorporating non-linear damage criteria, fracture criteria, cohesive forces, asymmetry and large deformation capabilities.
However, those models are not able to capture patient-specific cortical nor trabecular micro-architecture, which play a crucial role in bone strength [103,104,105][69][70][71].
Micro-scale models provide further insights into bone fracture prediction at smaller scales. Traditionally, micro-architectural features were assessed by means of histological sections [106][72] that lack in three-dimensionality. Nowadays, the input of micro-scale models often comes from micro-CT or SR images, that have a resolution able to non-destructively capture not only trabecular architecture, but even ultrastructural porosities, such as lacunae. However, this corresponds to higher computational costs, calculated by van Rietbergen et al. [107][73] through an element-by-element method that implies the use of uniformly shaped elements to reduce memory allocation and optimize computational times. Some issues arise when dealing with micro-CT or SR imaging techniques: filtration and segmentation. Reconstructed image data include noise that should be removed or at least reduced by filtering. The choice of an adequate filter (the Gaussian filter is the most suitable one, which is easily implementable and fast in computation [108][74]) is essential in order to obtain an input image for the model, as close as possible to the original sample. Another relevant aspect is the correct segmentation process that selects those voxels that are below or above a defined threshold, so as to separate those elements that are bone and those that can be considered as voids. This distinction is particularly relevant when dealing with the identification of micro-cracks and lacunae, whose typical size is significantly smaller (about 10 µm [72][38]) with respect to the trabecular architecture. Micro-FE models are often used for the prediction of bone fracture. For this purpose, specific damage criteria are implemented. In the work of Pistoia et al. [109][75], a micro-FE linear analysis is performed on the human distal radius. In order to predict bone failure, the chosen criterion is that the bone failure initiation occurs when bone is strained beyond a critical value, defined as the yield strain. This model is able to give a better prediction of bone failure loads (R2 = 0.75 correlation with experimental testing) with respect to macro-scale investigation techniques such as DXA measurements. Linear micro-FE models are also proposed for the study of the interaction between micro-cracks and micro-porosities, such as lacunae or surface discontinuities in bones. The role of the lacunar network in damage initiation and propagation is still unclear, due to the difficulty in obtaining dynamic visualization of the advancing crack. Micro-FE models shed some light on micro damage initiation and propagation. In this context, it is necessary to define a proper descriptor of the stress distribution, such as the strain energy density (SED) or the maximum principal stress (σ1) criteria. SED is a good predictor for the mechanical environment sensed by the osteocytes that reside in lacunae [110][76] and σ1 is a mechanical quantity often used to assess the failure in brittle materials [111][77]. Those two criteria show different sites of crack initiation and different directions for crack propagation (Figure 107).
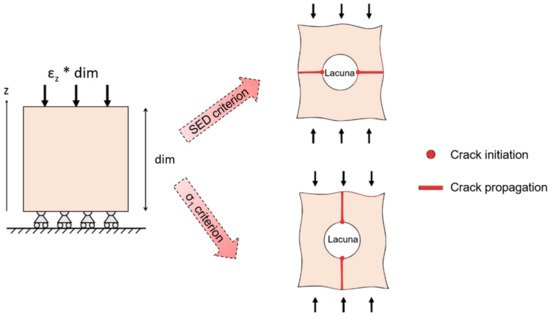Materials 14 01240 g010 550
Figure 107. Schematic output of models of a bone sample with a lacuna subjected to compression. Crack initiation (dots) and crack propagation (lines) are highlighted, according to strain energy density (SED) damage criterion and to σ1 criterion.
The σ1 criterion locates peak stresses and strains at regions matching with the experimental initiation stresses and strains found by Voide et al. [75][41]. Donaldson et al. [111][77] compare different linear micro-FE models that aim at the identification of crack initiation sites and of the role of the lacunar network. They present a relevant novelty by implementing a stress gradient model, schematized in Figure 118, that shows a clear directionality in the advancing crack (instead of the less realistic stress limit algorithm, that is able to simulate only accumulated damage around voids or surface discontinuities).
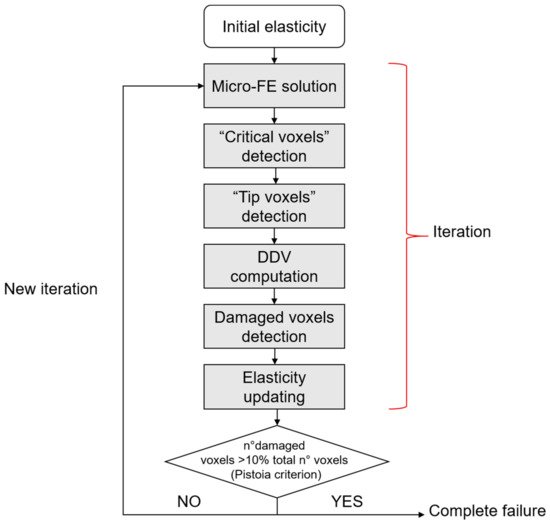Materials 14 01240 g011 550
Figure 118. Stress gradient algorithm. “Critical voxels” are the voxels that exceed a defined stress threshold. “Tip voxels” are the center of the spherical sensation region of the osteocytes and are eligible sites for damage propagation. In the stress gradient algorithm, a key role is played by the deletion direction vector (DDV), that indicates a direction for crack propagation. The iteration stops when the total failure of the sample is reached, according to the Pistoia criterion [109][75].
The stress gradient algorithm clarifies that damage starts from surface discontinuities or blood vessel (Figure 129) and not from lacunae, confirming from a computational point of view the hypothesis discussed in Section 3.
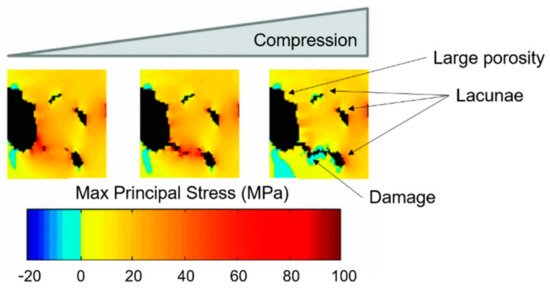Materials 14 01240 g012 550
Figure 129. Stress gradient algorithm (on SR CT data from a cortical bone sample) results: damage starts from big porosities and its propagation follows the stress gradient. Micro-damage is deviated by the presence of lacunae. Readapted from [111][77].
Despite the explained potentialities of linear micro-FE damage models, micro-damage predictions could be improved by implementing the bone non-linear behavior. The experimental tests focused on non-linear bone properties indicate ductile failure modes [112][78], in which damage is combined with the plasticity component of collagen fibers [113][79]. Hammond et al. [114][80] perform non-linear FE models (in this case, material non-linearity is considered) on trabecular samples from the distal femur of a human cadaver. They consider two micro-crack formation criteria, one for isotropic tissue models and one for anisotropic tissue models. For the isotropic tissue models, micro-cracks initiate if the ratio between maximum tensile principal stress and micro-crack initiation strength is equal to one. For anisotropic tissue models, micro-damage initiates if the maximum ratio between the normal of shear tractions with respect to the micro-crack initiation strength is equal to one. This non-linear micro-FE model is able to demonstrate that the anisotropy of bone tissue significantly contributes to bone fracture resistance [115][81]. Stipsitz et al. [116][82] try to implement an efficient micro-FE solver for large-scale non-linear simulations. However, the non-linearity of the system makes the results highly dependent on small structural deviations introduced by coarsening the structure. Additionally, one of the main drawbacks of the use of non-linear models is the increased computational cost, almost 10 times higher than linear simulations [87][53].
An increased degree of complexity can be found when analyzing nano-scale damage models that require further understanding of the variations in chemical pathways due to aging or disease. The first attempts in nano-scale bone fracture modeling were performed by Dubey et al. [117][83]: in their study, bone tissue fracture properties are based on the atomistic strength analyses of type I collagen in combination with hydroxyapatite interfacial arrangement, using molecular dynamics. Additional nano-scale studies [118][84] reveal that a decrease in the hydroxyapatite crystal size may change the mechanical behavior of the whole bone and the failure mode: from brittle-like crack-driven failure in larger crystals to a more widespread failure mode in the smaller ones. However, heterogeneities at the nano-scale remain difficult to model in a constitutive law and their role and effects are still unknown [119][85]. The impossibility to perform direct experimental tests on bone samples at the nano-scale is also a reason why those models are less considered for the purpose of this review.
To summarize, the increased image resolution and the optimization of parallel computational architecture for the solving of FE damage models seem promising tools for the improvement of the clinical understanding of fracture risk prediction. It is necessary to point out that some attempts in performing multiscale analyses have been performed by implementing bottom-up multiscale approaches, starting from the nano-scale up to the meso-scale [120][86] and analogously by Kwon et al. [121][87], who apply the multiscale analysis with variable geometrical parameters in order to determine its effect on the bone properties.
Before translating in silico damage models to clinical practice, the essential step is the experimental validation of the mentioned models that are still in their infancy, especially at smaller scales.

References

  1. Al-Lamki, L. Radiation Exposure from Medical Imaging: A Wake-up Call for Oman! Sultan Qaboos Univ. Med. J. 2011, 11, 1–4.
  2. Singh, M.; Nagrath, A.R.; Maini, P.S. Changes in trabecular pattern of the upper end of the femur as an index of osteoporosis. J. Bone Joint Surg. Am. 1970, 52, 457–467.
  3. Bouxsein, M.L.; Palermo, L.; Yeung, C.; Black, D.M. Digital X-ray radiogrammetry predicts hip, wrist and vertebral fracture risk in elderly women: A prospective analysis from the study of osteoporotic fractures. Osteoporos. Int. 2002, 13, 358–365.
  4. Huda, W.; Brad Abrahams, R. X-ray-based medical imaging and resolution. Am. J. Roentgenol. 2015, 204, W393–W397.
  5. Bilezikian, J.; Raisz, L.; Martin, T.J. Principles of Bone Biology, Two-Volume Set, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 1–2, ISBN 9780123738844.
  6. D’Elia, G.; Caracchini, G.; Cavalli, L.; Innocenti, P. Bone fragility and imaging techniques. Clin. Cases Miner. Bone Metab. 2009, 6, 234–246.
  7. Morris, R.M.; Yang, L.; Martín-Fernández, M.A.; Pozo, J.M.; Frangi, A.F.; Wilkinson, J.M. High-Spatial-Resolution Bone Densitometry with Dual-Energy X-ray Absorptiometric Region-free Analysis. Radiology 2015, 274, 532–539.
  8. IAEA International Atomic Energy Agency. Dual Energy X-ray Absorptiometry—Bone Mineral Densitometry|IAEA. Available online: (accessed on 24 February 2020).
  9. Zeytinoglu, M.; Jain, R.K.; Vokes, T.J. Vertebral fracture assessment: Enhancing the diagnosis, prevention, and treatment of osteoporosis. Bone 2017, 104, 54–65.
  10. El Maghraoui, A.; Roux, C. DXA scanning in clinical practice. QJM 2008, 101, 605–617.
  11. Schousboe, J.T.; DeBold, C.R. Reliability and accuracy of vertebral fracture assessment with densitometry compared to radiography in clinical practice. Osteoporos. Int. 2006, 17, 281–289.
  12. Adams, J.E. Quantitative computed tomography. Eur. J. Radiol. 2009, 71, 415–424.
  13. Brett, A.D.; Brown, J.K. Quantitative computed tomography and opportunistic bone density screening by dual use of computed tomography scans. J. Orthop. Transl. 2015, 3, 178–184.
  14. Kim, T.Y.; Schafer, A.L. Bariatric Surgery, Vitamin D, and Bone Loss. In Vitamin D: Fourth Edition; Elsevier: Amsterdam, The Netherlands, 2017; Volume 2, pp. 129–150. ISBN 9780128099650.
  15. Yu, E.W.; Thomas, B.J.; Brown, J.K.; Finkelstein, J.S. Simulated increases in body fat and errors in bone mineral density measurements by DXA and QCT. J. Bone Miner. Res. 2012, 27, 119–124.
  16. Jahng, J.S.; Kang, K.S.; Park, H.W.; Han, M.H. The Assessment of Bone Mineral Density in Postmenopausal and Senile Osteoporosis Using Quantitative Computed Tomography. J. Korean Orthop. Assoc. 1990, 25, 262.
  17. Link, T.M.; Majumdar, S.; Augat, P.; Lin, J.C.; Newitt, D.; Lane, N.E.; Genant, H.K. Proximal femur: Assessment for osteoporosis with T2* decay characteristics at MR imaging. Radiology 1998, 209, 531–536.
  18. Yablonskiy, D.A.; Haacke, E.M. Theory of NMR signal behavior in magnetically inhomogeneous tissues: The static dephasing regime. Magn. Reson. Med. 1994, 32, 749–763.
  19. Funke, M.; Bruhn, H.; Vosshenrich, R.; Rudolph, O.; Grabbe, E. Bestimmung der T2*-relaxationszeit zur charakterisierung des trabekularen knochens. RoFo 1994, 161, 58–63.
  20. Van Reeth, E.; Tham, I.W.K.; Tan, C.H.; Poh, C.L. Super-resolution in magnetic resonance imaging: A review. Concepts Magn. Reson. Part A 2012, 40A, 306–325.
  21. Nothnagle, P.; Chambers, W.; Davidson, M. Introduction to Stereomicroscopy. Available online: (accessed on 23 March 2020).
  22. Vanderoost, J. From histology to micro-CT: Measuring and modeling resorption cavities and their relation to bone competence. World J. Radiol. 2014, 6, 643.
  23. Mader, K.S.; Schneider, P.; Müller, R.; Stampanoni, M. A quantitative framework for the 3D characterization of the osteocyte lacunar system. Bone 2013, 57, 142–154.
  24. Schoenau, E.; Neu, C.M.; Beck, B.; Manz, F.; Rauch, F. Bone mineral content per muscle cross-sectional area as an index of the functional muscle-bone unit. J. Bone Miner. Res. 2002, 17, 1095–1101.
  25. Fedorov, A. Elettra Sincrotrone Trieste Elettra Sincrotrone Trieste. Available online: (accessed on 23 March 2020).
  26. Liu, X.S.; Zhang, X.H.; Rajapakse, C.S.; Wald, M.J.; Magland, J.; Sekhon, K.K.; Adam, M.F.; Sajda, P.; Wehrli, F.W.; Guo, X.E. Accuracy of high-resolution in vivo micro magnetic resonance imaging for measurements of microstructural and mechanical properties of human distal tibial bone. J. Bone Miner. Res. 2010, 25, 2039–2050.
  27. Poundarik, A.A.; Vashishth, D. Multiscale imaging of bone microdamage. Connect. Tissue Res. 2015, 56, 87–98.
  28. Fouquet, C.; Gilles, J.F.; Heck, N.; Santos, M.D.; Schwartzmann, R.; Cannaya, V.; Morel, M.P.; Davidson, R.S.; Trembleau, A.; Bolte, S. Improving axial resolution in confocal microscopy with new high refractive index mounting media. PLoS ONE 2015, 10.
  29. Dufrêne, Y.F. Atomic force microscopy, a powerful tool in microbiology. J. Bacteriol. 2002, 184, 5205–5213.
  30. Acevedo, C.; Stadelmann, V.A.; Pioletti, D.P.; Alliston, T.; Ritchie, R.O. Fatigue as the missing link between bone fragility and fracture. Nat. Biomed. Eng. 2018, 2, 62–71.
  31. Daffner, R.H.; Pavlov, H. Stress fractures: Current concepts. AJR Am. J. Roentgenol. 1992, 159, 245–252.
  32. Taylor, D. Fracture and repair of bone: A multiscale problem. J. Mater. Sci. 2007, 42, 8911–8918.
  33. Shi, X.; Liu, X.; Wang, X.; Guo, X.; Niebur, G.L. Type and orientation of yielded trabeculae during overloading of trabecular bone along orthogonal directions. J. Biomech. 2010, 43, 2460–2466.
  34. Gibson, L.J. Biomechanics of cellular solids. J. Biomech. 2005, 38, 377–399.
  35. Fyhrie, D.; Schaffler, M.B. Failure mechanisms in human vertebral cancellous bone. Bone 1994, 15, 105–109.
  36. Zimmermann, E.A.; Busse, B.; Ritchie, R.O. The fracture mechanics of human bone: Influence of disease and treatment. Bonekey Rep. 2015, 4.
  37. Vashishth, D. Hierarchy of bone microdamage at multiple length scales. Int. J. Fatigue 2007, 29, 1024–1033.
  38. Voide, R.; Schneider, P.; Stauber, M.; van Lenthe, G.H.; Stampanoni, M.; Müller, R. The importance of murine cortical bone microstructure for microcrack initiation and propagation. Bone 2011, 49, 1186–1193.
  39. Taylor, D.; Hazenberg, J.G.; Lee, T.C. Living with cracks: Damage and repair in human bone. Nat. Mater. 2007, 6, 263–268.
  40. Buikstra, J.E. Ortner’s Identification of Pathological Conditions in Human Skeletal Remains; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128097380.
  41. Voide, R.; Schneider, P.; Stauber, M.; Wyss, P.; Stampanoni, M.; Sennhauser, U.; van Lenthe, G.H.; Müller, R. Time-lapsed assessment of microcrack initiation and propagation in murine cortical bone at submicrometer resolution. Bone 2009, 45, 164–173.
  42. Akhter, M.P.; Kimmel, D.B.; Lappe, J.M.; Recker, R.R. Effect of Macroanatomic Bone Type and Estrogen Loss on Osteocyte Lacunar Properties in Healthy Adult Women. Calcif. Tissue Int. 2017, 100, 619–630.
  43. Currey, J.D. Stress Concentrations in Bone. J. Cell Sci. 1962, s3-103, 111–133.
  44. McNamara, L.M.; Van Der Linden, J.C.; Weinans, H.; Prendergast, P.J. Stress-concentrating effect of resorption lacunae in trabecular bone. J. Biomech. 2006, 39, 734–741.
  45. Qiu, S.; Rao, S.D.; Fyhrie, D.P.; Palnitkar, S.; Parfitt, M.A. The morphological association between microcracks and osteocyte lacunae in human cortical bone. Bone 2005.
  46. Courtney, A.C.; Hayes, W.C.; Gibson, L.J. Age-related differences in post-yield damage in human cortical bone. Experiment and model. J. Biomech. 1996, 29, 1463–1471.
  47. Carter, D.R.; Hayes, W.C.; Schurman, D.J. Fatigue life of compact bone-II. Effects of microstructure and density. J. Biomech. 1976, 9, 211–218.
  48. Vashishth, D.; Behiri, J.C.; Bonfield, W. Crack growth resistance in cortical bone: Concept of microcrack toughening. J. Biomech. 1997, 30, 763–769.
  49. Schaffler, M.B.; Radin, E.L.; Burr, D.B. Mechanical and morphological effects of strain rate on fatigue of compact bone. Bone 1989, 10, 207–214.
  50. Awaji, H.; Ebisudani, M.; Choi, S.-M.; Ohashi, T. Crack Deflection Toughening Mechanism in Brittle Materials. In Fracture Resistance Testing of Monolithic and Composite Brittle Materials; ASTM International: West Conshohocken, PA, USA, 2009; pp. 137–151.
  51. Gautieri, A.; Vesentini, S.; Redaelli, A.; Buehler, M.J. Hierarchical structure and nanomechanics of collagen microfibrils from the atomistic scale up. Nano Lett. 2011, 11, 757–766.
  52. Travert, C.; Jolivet, E.; Sapin-De Brosses, E.; Mitton, D.; Skalli, W. Sensitivity of patient-specific vertebral finite element model from low dose imaging to material properties and loading conditions. Med. Biol. Eng. Comput. 2011, 49, 1355–1361.
  53. Christen, D.; Webster, D.J.; Müller, R. Multiscale modelling and nonlinear.nite element analysis as clinical tools for the assessment of fracture risk. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 2653–2668.
  54. Dagan, D.; Be’ery, M.; Gefen, A. Single-trabecula building block for large-scale finite element models of cancellous bone. Med. Biol. Eng. Comput. 2004, 42, 549–556.
  55. Van Rietbergen, B.; Odgaard, A.; Kabel, J.; Huiskes, R. Relationships between bone morphology and bone elastic properties can be accurately quantified using high-resolution computer reconstructions. J. Orthop. Res. 1998, 16, 23–28.
  56. Niebur, G.L.; Feldstein, M.J.; Yuen, J.C.; Chen, T.J.; Keaveny, T.M. High-resolution finite element models with tissue strength asymmetry accurately predict failure of trabecular bone. J. Biomech. 2000, 33, 1575–1583.
  57. Ilic, S.; Hackl, K.; Gilbert, R. Application of the multiscale FEM to the modeling of cancellous bone. Biomech. Model. Mechanobiol. 2010, 9, 87–102.
  58. Wolff, J. The Law of Bone Remodeling; Springer: Berlin/Heidelberg, Germany, 1986.
  59. Sen, C.; Prasad, J. Exploring conditions that make cortical bone geometry optimal for physiological loading. Biomech. Model. Mechanobiol. 2019, 18, 1335–1349.
  60. Lengsfeld, M.; Schmitt, J.; Alter, P.; Kaminsky, J.; Leppek, R. Comparison of geometry-based and CT voxel-based finite element modelling and experimental validation. Med. Eng. Phys. 1998, 20, 515–522.
  61. Webster, D.; Müller, R. In silico models of bone remodeling from macro to nano-from organ to cell. Wiley Interdiscip. Rev. Syst. Biol. Med. 2011, 3, 241–251.
  62. Hambli, R. A quasi-brittle continuum damage finite element model of the human proximal femur based on element deletion. Med. Biol. Eng. Comput. 2013, 51, 219–231.
  63. Robinson, D.L.; Jiang, H.; Song, Q.; Yates, C.; Lee, P.V.S.; Wark, J.D. The application of finite element modelling based on clinical pQCT for classification of fracture status. Biomech. Model. Mechanobiol. 2019, 18, 245–260.
  64. Viceconti, M.; Taddei, F.; Van Sint Jan, S.; Leardini, A.; Cristofolini, L.; Stea, S.; Baruffaldi, F.; Baleani, M. Multiscale modelling of the skeleton for the prediction of the risk of fracture. Clin. Biomech. 2008, 23, 845–852.
  65. Cowin, S. Bone stress adaptation models. J. Biomech. Eng. 1993, 115, 528–533.
  66. Schileo, E.; Taddei, F.; Malandrino, A.; Cristofolini, L.; Viceconti, M. Subject-specific finite element models can accurately predict strain levels in long bones. J. Biomech. 2007, 40, 2982–2989.
  67. Taddei, F.; Schileo, E.; Helgason, B.; Cristofolini, L.; Viceconti, M. The material mapping strategy influences the accuracy of CT-based finite element models of bones: An evaluation against experimental measurements. Med. Eng. Phys. 2007, 29, 973–979.
  68. Imai, K.; Ohnishi, I.; Bessho, M.; Nakamura, K. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine 2006, 31, 1789–1794.
  69. Harrison, N.M.; McDonnell, P.; Mullins, L.; Wilson, N.; O’Mahoney, D.; McHugh, P.E. Failure modelling of trabecular bone using a non-linear combined damage and fracture voxel finite element approach. Biomech. Model. Mechanobiol. 2013, 12, 225–241.
  70. Jensen, K.; Mosekilde, L. A model of vertebral trabecular bone architecture and its mechanical properties. Bone 1990, 11, 417–423.
  71. Boutroy, S.; Van Rietbergen, B.; Sornay-Rendu, E.; Munoz, F.; Bouxsein, M.L.; Delmas, P.D. Finite element analysis based on in vivo HR-pQCT images of the distal radius is associated with wrist fracture in postmenopausal women. J. Bone Miner. Res. 2008, 23, 392–399.
  72. Carbonare, L.D.; Valenti, M.; Bertoldo, F.; Zanatta, M.; Zenari, S.; Realdi, G.; Cascio, V.L.; Giannini, S. Bone microarchitecture evaluated by histomorphometry. Micron 2005, 36, 609–615.
  73. van Rietbergen, B.; Weinans, H.; Huiskes, R.; Odgaard, A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite-element models. J. Mech. 1995, 28, 69–81.
  74. Bouxsein, M.L.; Boyd, S.K.; Christiansen, B.A.; Guldberg, R.E.; Jepsen, K.J.; Müller, R. Guidelines for assessment of bone microstructure in rodents using micro-computed tomography. J. Bone Miner. Res. 2010, 25, 1468–1486.
  75. Pistoia, W.; Lill, C.A.; Eckstein, F.; Rietbergen, B.V.A.N.; Lochmu, E.; Ru, P. Estimation of Distal Radius Failure Load With Micro-Finite Element Analysis Models Based on Three-dimensional Peripheral Quantitative Computed Tomography Images. Bone 2002, 30, 842–848.
  76. Webster, D.; Schulte, F.A.; Lambers, F.M.; Kuhn, G.; Müller, R. Strain energy density gradients in bone marrow predict osteoblast and osteoclast activity: A finite element study. J. Biomech. 2015, 48, 866–874.
  77. Donaldson, F.; Ruffoni, D.; Schneider, P.; Levchuk, A.; Zwahlen, A.; Pankaj, P.; Müller, R. Modeling microdamage behavior of cortical bone. Biomech. Model. Mechanobiol. 2014, 13, 1227–1242.
  78. Nalla, R.; Kruzic, J.; Kinney, J.; Ritchie, R.O. Mechanistic aspects of fracture and R-curve behavior in human cortical bone. Biomaterials 2005, 26, 217–231.
  79. Thurner, P.J.; Wyss, P.; Voide, R.; Stauber, M.; Stampanoni, M.; Sennhauser, U.; Müller, R. Time-lapsed investigation of three-dimensional failure and damage accumulation in trabecular bone using synchrotron light. Bone 2006, 39, 289–299.
  80. Hammond, M.A.; Wallace, J.M.; Allen, M.R.; Siegmund, T. Mechanics of linear microcracking in trabecular bone. J. Biomech. 2019, 83, 34–42.
  81. Demirtas, A.; Ural, A. Material heterogeneity, microstructure, and microcracks demonstrate differential influence on crack initiation and propagation in cortical bone. Biomech. Model. Mechanobiol. 2018, 17, 1415–1428.
  82. Stipsitz, M.; Zysset, P.K.; Pahr, D.H. Efficient materially nonlinear μ FE solver for simulations of trabecular bone failure. Biomech. Model. Mechanobiol. 2020, 19, 861–874.
  83. Dubey, D.K.; Tomar, V. Microstructure dependent dynamic fracture analyses of trabecular bone based on nascent bone atomistic simulations. Mech. Res. Commun. 2008, 35, 24–31.
  84. Libonati, F.; Nair, A.K.; Vergani, L.; Buehler, M.J. Fracture mechanics of hydroxyapatite single crystals under geometric confinement. J. Mech. Behav. Biomed. Mater. 2013, 20, 184–191.
  85. Tai, K.; Dao, M.; Suresh, S.; Palazoglu, A.; Ortiz, C. Nanoscale heterogeneity promotes energy dissipation in bone. Nat.Mater. 2007, 6, 454–462.
  86. Hamed, E.; Jasiuk, I.; Yoo, A.; Lee, Y.H.; Liszka, T. Multi-scale modelling of elastic moduli of trabecular bone. J. R. Soc. Interface 2012, 9, 1654–1673.
  87. Kwon, Y.W.; Clumpner, B.R. Multiscale modeling of human bone. Multiscale Multidiscip. Model. Exp. Des. 2018, 1, 133–143.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Academic Video Service
Feedback