1. Introduction

Introduction

The χ2 test was introduced by Pearson in 1900^[1]. The 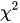 χ² statistic were originally devised to measure the departure in a system of n (random normally distributed) variables {y₁, …, y_n} having each a series of undefined number of observations (y₁ = {y_1,1, …}, …, y_n = {y_n,1, …}) for which {x₁, …, x_n} are the means and {σ₁, …, σ_n} are the deviations. In this context the formula for the 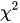χ² statistic is derived and it have a known distribution function.

\( PDF_{\chi^2}(x; n) = \frac{x^{n/2-1}e^{-x/2}}{2^{n-2}\Gamma(n/2)}, CDF_{\chi^2}(x; n) = \frac{1}{\Gamma(n/2)}\int_{0}^{x/2}{t^{n/2-1}e^{-t}dt} \)

It should be noted that the context in which the 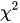χ² statistic is slightly different than the one in which is currently in use. This is the reason for which, during time a series of patches have been made to the statistic in order to make it usable.

For instance, in the contingency of two factors f1 = {f1₁, f1₂} and f2 = {f2₁, f2₂}, under the assumption that x_i,j ~ f1_if2_j:

the use of the 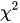χ² assumes that it exists also a series of observations behind each of the {x_1,1, x_1,2, x_2,1, x_2,2} entries in the table above, and someone may calculate the X² statistic (e.g. X² is the sample based statistic, while  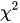is the population based statistic or distribution) for the contingency as:

X² =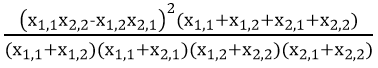 

Since the estimation of expected frequencies in the contingency of the factors uses rows totals {x_1,1 + x_1,2, x_2,1 + x_2,2}, columns totals {x_1,2 + x_2,1, x_2,1 + x_2,2} and overall total {x_1,1 + x_1,2 + x_2,1 + x_2,2} the variation in the X² is constrained. Are exactly three independent constrains (if x_1,1 + x_1,2 + x_2,1 + x_2,2 = n₀, x_1,1 + x_1,2 = n₁, x_1,2 + x_2,1 = n₂ then the rows totals are {n₁, n₀ - n₁}, the columns totals are {n₂, n₀ - n₂}, and the overall total is {n₀}) and it is exactly one degree of freedom for X² (if x_1,1 = x, then x_1,2 = n₁ - x, x_2,1 = n₂ - x, x_2,2 = n₀ - n₁ - n₂ + x) and therefore the probability associated with the X² value should be taken from 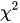χ² distribution with 1 degree of freedom. More, it can be verified by induction that for a m·n contingency table are m + n - 1 independent constrains, and thus are m·n - m - n +1 degrees of freedom.

The main trouble in the use of the 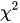χ² statistic is the fact that its distribution is asserted and the probability is derived under the assumption that behind {x_1,1, x_1,2, x_2,1, x_2,2} values are a infinite number of observations ({y_1,1,1, …}, {y_,1,2,1, …}, {y_2,1,1, …}, {y_2,2,1, …}), which actually is not true never. Even if are accessible some population means, {μ_1,1, μ_1,2, μ_2,1, μ_2,2} those means comes actually from some estimations made from some (finite) samples of the populations, which passes sampling noises (or errors) to the statistic itself. A clear shot to this matter has been made by the Fisher which patches the 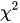χ² statistic in the case of the 2x2 contingency above given for the frequency tables (Fisher exact test, see ^[2]).

Despite of its use in goodness-of fit tests, actually the 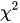χ² statistic is not suitable in this instance. Having a series of observations {o₁, …, o_n} one split the domain of the observations (or having a series of cumulative probabilities {q₁, …, q_n} associated with the series of sorted observations, see ^[3]) in an arbitrary number of subintervals (usually taken as 1 + ) in order to construct the series of observed and expected frequencies. By this fact alone, when it is used to test the goodness-of, the 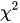χ² statistic is itself exposed to the risk of being in error. Turning back to the general assumption in which its formula were derived - namely the assumption that behind each observed frequency is an infinite number of observations - one may realize that this kind of state of facts is never meet in practice. Therefore, only for very large samples, in which the observed frequencies are 'large enough' too, the 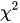χ² statistic may become of use.

Someone may ask now: Which are the subjects in which the 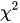χ² statistic is of use? - And indeed are, but the answer is not detailed here.

2. Measures of agreement in contingencies of multiplicative effects

Measures of agreement in contingencies of multiplicative effects

Something else is of interest in close connection with the use of the 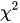χ² statistic for contingency tables, as firstly pointed out by Fisher in ^[4], namely its depeconndence on ection with the experimental design toon which it is applied. In ^[5] is revised and generalized this perspective, and here is given athe summary of it.

Let's consider a series of observations made in a contingency of two factors (see the table below; the experimental design can be generalized to any number of factors) which affect the observation in a multiplicative manner (e.g. u_i,j  fr_i·fc_j).

Above (u_i,j)_1≤i≤r,_1≤j≤c are the observations made under different constrains of the factors, where (fr_i)_1≤i≤r are the levels of the fr factor and (fc_j)_1≤j≤c are the levels of the fc factor. For convenience of the later use, also the sums sr₁ (sr₁ = u_1,1 + … + u_1,c), …, sr_r (sr_c = u_r,1 + … + u_r,c), sc₁ (sc₁ = u_1,1 + … + u_r,1), …, sc_c (sc_c = u_1,c + … + u_r,c), and ss = Σ_1≤i≤r,_1≤j≤cu_i,j were assigned.

It can be prooved [where?] fed that under the presence of the multiplicative effect of the two (fr and fc) factors a very good estimate of the expected values would be given [is given?] by the formula v_i,j = sr_i·sc_j/ss (see the table below).

The values of the factors ((fr_i)_1≤i≤r and (fc_j)_1≤j≤c) are in general unknown, but even if are known, doesn't help too much in the analysis since also their values may be affected by errors, as the observations (u_i,j)_1≤i≤r,_1≤j≤c are supposed to be.

Either way (the values of the factors are known or not) in the calculation of the expected values (v_i,j)_1≤i≤r,_1≤j≤c are used the sums of the observations (sr_i = Σ_1≤j≤cu_i,j, sc_j = Σ_1≤i≤ru_i,j, ss = Σ_1≤i≤r,_1≤j≤cu_i,j) as the estimates for the factor levels (or values):

fr₁ : … : fr_i : … fr_r  sr₁ : … : sr_i : … sr_r & fc₁ : … : fc_i : … fc_c  sc₁ : … : sc_i : … sc_c

Three alternative assumptions may push further the analysis and are on the regard of the type of the error (possibly, probably) made in the process of observation. Since the whole process of observation under the influence of the factors is a part of a whole, it is safely to assume that the error keeps its type during the process of observation, it is random and it is accidentally (having a low occurrence) and the three alternatives along with their consequences as usable formulas are listed in the table below.

It should be noted that X² formula is usable only in the assumption that fr_i, fc_j > 0.

The S² formula minimizes the absolute errors, V² formula minimizes the relative errors, while X² formula minimizes the X² value for the contingency.

The algorithm is:

• for(1 ≤ i ≤ r and 1 ≤ j ≤ c) v_i,j ← sr_i·sc_j/ss
• fr₁ = fc₁ = (v_1,1)^1/2; for(2 ≤ i ≤ r) sr_i ← v_i,1/fc₁; for(2 ≤ j ≤ c) sc_j ← v_1,j/fr₁
• Repeat
  • for(1 ≤ i ≤ r) fr_i ← Corresponding "Consequenced usable formula" (from S², V², or X²)
  • for(1 ≤ j ≤ c) fc_j ← Corresponding "Consequenced usable formula" (from S², V², or X²)
• Until convergence criteria is meet.

It has been shown in ^[5] that consecutive using of equations given as usable formulas converges fast to the minimum (constraint formula) and thus provides better estimates of the factor levels (fr_i)_1≤i≤r and (fc_j)_1≤j≤c which can be further used to improve the expected estimates (population means) of the factorial experiment: v_i,j ← fr_i·fc_j. Using the data given in ^[5] the number of steps for a change less than 0.1% in the objective function (S², V², and X² respectively) are: 2 steps for S² and X² and 3 steps for V².

3. Exploiting the agreement in contingencies of multiplicative effects

Exploiting the agreement in contingencies of multiplicative effects

One of the uses of the χ² statistic is in the presence of censored data (see for instance ^[6] and ^[7]).

A recent application of the method above described has been reported in ^[8]. The method has been used to fill the gaps of missing data in contingencies of multiplicative effects of factors influencing the observations. The algorithm above given must be adapted in order to meet the requirements to be used and also the gaps may be filled if exists at least one observation in each row (e.g. sr_i ≠ 0 for 1 ≤ i ≤ r) and at least one observation in each column (e.g. sc_j ≠ 0 for 1 ≤ j ≤ c).

In the most general case, a recursive procedure can be designed to fill the gaps. Later on, the procedure of minimizing the residuals (e.g. S², V² or X²) goes smoothly. The full program (PHP source code) is in the appendix (as a coeditor noted, an encyclopedia is not a place to put computer code). Here is given (an example of) raw data and data filled with gaps, followed by the optimization of the expectances, of the S², V² and X² respectively.

Raw data ("data.txt" input data for the program given in the appendix)

 Data with gaps (18 randomly filled values from raw data)

Expected values ((Σ_io_i,j)·(Σ_jo_i,j)/(Σ_i,jo_i,j)) calculated from data with gaps

Optimized expectances for S² → min.

S² = 3.4052, V² = 0.0095, X² = 0.1776

Optimized expectances for V² → min.

S² = 3.7697, V² = 0.0089, X² = 0.1812

Optimized expectances for X² → min.

S² = 3.5072, V² = 0.0090, X² = 0.1751

The program given in the appendix can be feed on any data with gaps (like the example below) to fill the gaps (like the filled gaps) doing this by optimizing the expectances (three alternatives, S², V² and X² respectively).Appendix - program filling the data with gaps and computing the expected values in the gaps (PHP source code)

Appendix - program filling the data with gaps and computing the expected values in the gaps (PHP source code)

[A long uncommented computer code listing does not belong in an encyclopedia! RDG]

function get_all(&$o){

//get the data from data.txt file

$a = explode("\r\n",file_get_contents("data.txt"));

$o = array(); for($i = 0; $i < count($a); $i++){$o[$i] = explode("\t",$a[$i]); }

}

function gen_mat($plus){

//censor the data from data.txt file

$a = explode("\r\n",file_get_contents("data.txt"));

$o = array(); for($i = 0; $i < count($a); $i++){$o[$i] = explode("\t",$a[$i]); }

$n = count($o); $m = count($o[0]);

for($i = 0; $i < $n; $i++)for($j = 0; $j < $m; $j++)$q[$i][$j] = ""; //gaps

everywhere here

for($i = 0; $i < $n; $i++){$j = rand(0,$m-1); $q[$i][$j] = $o[$i][$j]; }

//some gaps filled with values in lines (n)

for($j = 0; $j < $m; $j++){$i = rand(0,$n-1); $q[$i][$j] = $o[$i][$j]; }

//some gaps filled with values in columns (m)

//gapped data file should have at least one nonempty value on each line and column

foor($k = 0; $k < $plus; $k++){

for($add_plus = 0; $add_plus < $plus - $m - $n; ){

$i = rand(0,$n-1); $j = rand(0,$m-1);

if(($q[$i][$j] = = = "")){$q[$i][$j] = $o[$i][$j]; $add_plus++; }

}

}

$r = array(); for($i = 0; $i < $n; $i++)$r[$i] = implode("\t",$q[$i]);

file_put_contents("data_censored.txt",implode("\r\n",$r));

}

function get_mat(&$o){

//get censored data

$a = explode("\r\n",file_get_contents("data_censored.txt"));

$o = array(); for($i = 0; $i < count($a); $i++){$o[$i] = explode("\t",$a[$i]); }

}

function set_mat(&$o,&$q){

//copy o into q

$q = array();

for($i = 0; $i < count($o); $i++)for($j = 0; $j < count($o[0]); $j++)$q[$i][$j] = $o[$i][$j];

}

function set1mat(&$o,&$q){ //copy only nonempty

values from o into q

foor($i = 0; $i < count($o); $i++)for($j = 0; $j < count($o[0]); $j++)if(!($o[$i][$j] = = = ""))$q[$i][$j] = $o[$i][$j];

}

function expect(&$a,&$b){$ss = 0.0; $sr = array(); $sc = array(); $b = array();

for($i = 0; $i < count($a); $i++){

$sr[$i] = 0.0; for($j = 0; $j < count($a[$i]); $j++)$sr[$i]+ = $a[$i][$j];

} //calculate

row sums

for($j = 0; $j < count($a[0]); $j++){

$sc[$j] = 0.0; for($i = 0; $i < count($a); $i++)$sc[$j]+ = $a[$i][$j];

}

//calculate column sums

for($i = 0; $i < count($a); $i++)for($j = 0; $j < count($a[$i]); $j++)$ss+ = $a[$i][$j];

for($i = 0; $i < count($a); $i++)for($j = 0; $j < count($a[$i]); $j++)$b[$i][$j] = $sr[$i]*$sc[$j]/$ss;

} //calculate expectances

function estim1(&$b,&$r,&$c){

$r = array(); $r[0] = sqrt($b[0][0]);

$c = array(); $c[0] = sqrt($b[0][0]);

for($i = 1; $i < count($b); $i++)$r[$i] = $b[$i][0]/$c[0];

for($i = 1; $i < count($b[0]); $i++)$c[$i] = $b[0][$i]/$r[0];

} //iterate expectances

function af_mat(&$a){$r = array(); $t = array();

for($i = 0; $i < count($a); $i++){

for($j = 0; $j < count($a[0]); $j++)

$r[$i][$j] = trim(sprintf("%.3f",$a[$i][$j]));

$t[$i] = implode("\t",$r[$i]);

}

//display predicted data

file_put_contents("data_pred.txt",implode("\r\n",$t));

}

function val2S(&$a,&$r,&$c){

$s = 0.0; for($i = 0; $i < count($r); $i++)for($j = 0; $j < count($c); $j++)if(!($a[$i][$j] = = = ""))$s+ = pow($a[$i][$j]-$r[$i]*$c[$j],2); return($s);

} //iterate S^2 alternative 

function val2V(&$a,&$r,&$c){

$s = 0.0; for($i = 0; $i < count($r); $i++)for($j = 0; $j < count($c); $j++)if(!($a[$i][$j] = = = ""))$s+ = pow($a[$i][$j]-$r[$i]*$c[$j],2)/pow($r[$i]*$c[$j],2); return($s);

} //iterate V^2 alternative

function val2X(&$a,&$r,&$c){

$s = 0.0; for($i = 0; $i < count($r); $i++)for($j = 0; $j < count($c); $j++)if(!($a[$i][$j] = = = ""))$s+ = pow($a[$i][$j]-$r[$i]*$c[$j],2)/($r[$i]*$c[$j]); return($s);

} //iterate X^2 alternative

function af1mat($s,&$o,&$a,&$rf,&$cf){$r = array(); $t = array();

for($i = 0; $i < count($a); $i++){

for($j = 0; $j < count($a[0]); $j++)

$r[$i][$j] = trim(sprintf("%.3f",$a[$i][$j]));

$t[$i] = implode("\t",$r[$i]);

}

//display a resulted matrix

$u = implode("\r\n",$t);

$v = array(); for($i = 0; $i < count($rf); $i++)$v[$i] = trim(sprintf("%.3f",$rf[$i]));

$u. = "\r\nRows factors:\r\n".implode("\t",$v);

$v = array(); for($j = 0; $j < count($cf); $j++)$v[$j] = trim(sprintf("%.3f",$cf[$j]));

$u. = "\r\nCols factors:\r\n".implode("\t",$v);

$u. = "\r\nS2 = ".sprintf("%.4f",val2S($o,$rf,$cf));

$u. = "\r\nV2 = ".sprintf("%.4f",val2V($o,$rf,$cf));

$u. = "\r\nX2 = ".sprintf("%.4f",val2X($o,$rf,$cf));

file_put_contents("data_".$s."_min.txt",$u);

}

function not_empty(&$a){

for($i = 0; $i < count($a); $i++)for($j = 0; $j < count($a[0]); $j++)if(!($a[$i][$j] = = = ""))return(array($i,$j));

} //return first nonempty entry

function fill_recurs($i,$j,&$a,&$r,&$c){

//fill

recursive the gaps from the entry point

$i_ = array();

for($k = 0; $k < count($r); $k++)if($k < >$i){

if($a[$k][$j] = = = "")continue;

$r[$k] = $a[$k][$j]/$c[$j]; $i_[] = $k;

}

$j_ = array();

for($l = 0; $l < count($c); $l++)if($l < >$j){

if($a[$i][$l] = = = "")continue;

$c[$l] = $a[$i][$l]/$r[$i]; $j_[] = $l;

}

for($k = 0; $k < count($r); $k++)if(!($r[$k] = = = ""))

for($l = 0; $l < count($c); $l++)if(!($c[$l] = = = ""))

if(($a[$k][$l] = = = ""))$a[$k][$l] = $r[$k]*$c[$l];

for($k = 0; $k < count($r); $k++)if(!($r[$k] = = = ""))

for($l = 0; $l < count($c); $l++)if(!($a[$k][$l] = = = ""))

if(($c[$l] = = = ""))$c[$l] = $a[$k][$l]/$r[$k];

for($l = 0; $l < count($c); $l++)if(!($c[$l] = = = ""))

for($k = 0; $k < count($r); $k++)if(!($a[$k][$l] = = = ""))

if(($r[$k] = = = ""))$r[$k] = $a[$k][$l]/$c[$l];

$empty = 0;

for($k = 0; $k < count($r); $k++)

for($l = 0; $l < count($c); $l++)if(($a[$k][$l] = = = ""))$empty++;

if($empty>0){

for($k = 0; $k < count($i_); $k++)

for($l = 0; $l < count($j_); $l++)

fill_recurs($i_[$k],$j_[$l],$a,$r,$c);

}

}

function opti_iterat(&$o,&$q){

//optimize the expectances

for($i = 0; $i < 20; $i++){

set1mat($o,$q); expect($q,$e); set_mat($e,$q);

}

}

function sum_row($i,&$a,&$c,$pa,$pc){

//apply a sum function to a row

$t = 0.0;

for($j = 0; $j < count($c); $j++){

$ta = pow($a[$i][$j],$pa); $tc = pow($c[$j],$pc); $t+ = $ta*$tc;

}

return($t);

}

function sum_col($j,&$a,&$r,$pa,$pr){

//apply a sum function to a column

$t = 0.0;

for($i = 0; $i < count($r); $i++){

$ta = pow($a[$i][$j],$pa); $tr = pow($r[$i],$pr); $t+ = $ta*$tr;

}

return($t);

}

function estim2S(&$a,&$r,&$c){

for($i = 0; $i < count($r); $i++)

$r[$i] = sum_row($i,$a,$c,1,1)/sum_row($i,$a,$c,0,2);

for($j = 0; $j < count($c); $j++)

$c[$j] = sum_col($j,$a,$r,1,1)/sum_col($j,$a,$r,0,2);

for($i = 0; $i < count($r); $i++)for($j = 0; $j < count($c); $j++)$a[$i][$j] = $r[$i]*$c[$j];

} //estimate for S^2 to min

function estim2V(&$a,&$r,&$c){

for($i = 0; $i < count($r); $i++)

$r[$i] = sum_row($i,$a,$c,2,-2)/sum_row($i,$a,$c,1,-1);

for($j = 0; $j < count($c); $j++)

$c[$j] = sum_col($j,$a,$r,2,-2)/sum_col($j,$a,$r,1,-1);

for($i = 0; $i < count($r); $i++)for($j = 0; $j < count($c); $j++)$a[$i][$j] = $r[$i]*$c[$j];

} //estimate for V^2 to min

function estim2X(&$a,&$r,&$c){

for($i = 0; $i < count($r); $i++)

$r[$i] = sqrt(sum_row($i,$a,$c,2,-1)/sum_row($i,$a,$c,0,1));

for($j = 0; $j < count($c); $j++){

$c[$j] = sqrt(sum_col($j,$a,$r,2,-1)/sum_col($j,$a,$r,0,1));

}

for($i = 0; $i < count($r); $i++)for($j = 0; $j < count($c); $j++)$a[$i][$j] = $r[$i]*$c[$j];

} //estimate for X^2 to min

//main program begins here

get_all($o_all); //get data.txt

gen_mat(0); //make data_censored.txt (data with gaps)

get_mat($o); //get censored data from data_censored.txt (data with gaps)

set_mat($o,$q); //make a copy of the censored data

$r = array(); for($i = 0; $i < count($q); $i++)$r[$i] = ""; //empty row factors

$c = array(); for($j = 0; $j < count($q[0]); $j++)$c[$j] = ""; //empty column factors

list($i,$j) = not_empty($q); $r[$i] = sqrt($q[$i][$j]); $c[$j] = sqrt($q[$i][$j]); //estimated factors from first nonempty value

fill_recurs($i,$j,$q,$r,$c); //recursively filled values from nonempty values

opti_iterat($o,$q); //optimize for expectances

af_mat($q); //display the result as data_pred.txt file

set_mat($q,$qS2); //prepare for S^2 to min optimization

estim1($qS2,$rS2,$cS2);

for($k = 1; $k < 20; $k++){set1mat($o,$qS2); estim2S($qS2,$rS2,$cS2); }

af1mat("S2",$o,$qS2,$rS2,$cS2); //display S^2 to min optimization result

set_mat($q,$qV2); //prepare for V^2 to min optimization

estim1($qV2,$rV2,$cV2);

for($k = 1; $k < 20; $k++){set1mat($o,$qV2); estim2V($qV2,$rV2,$cV2); }

af1mat("V2",$o,$qV2,$rV2,$cV2); //display V^2 to min optimization result

set_mat($q,$qX2); //prepare for X^2 to min optimization

estim1($qX2,$rX2,$cX2);

for($k = 1; $k < 20; $k++){set1mat($o,$qX2); estim2X($qX2,$rX2,$cX2); }

af1mat("X2",$o,$qX2,$rX2,$cX2); //di

for($k=1;$k<20;$k++){splet1may X^2 to min optit($o,$qX2);estim2X($qX2,$rX2,$cX2);}

af1mization result("X2",$o,$qX2,$rX2,$cX2);