Mathematical models predict corrosion inhibition

Mathematical models predict corrosion inhibition: Comparison

Please note this is a comparison between Version 12 by Evelin Gutiérrez and Version 11 by Evelin Gutiérrez.

The use of corrosion inhibitors is an important method to retard the process of metallic attack by corrosion. The construction of mathematical models from theoretical-computational and experimental data obtained for different molecules is one of the most attractive alternatives in the analysis of corrosion prevention, whose objective is to define those molecular characteristics that are common in high-performance corrosion inhibitors.

corrosion inhibition
organic inhibitors
theoretical studies
molecular descriptors
mathematical models

1. Introduction

Corrosion is defined as the destructive attack of a material by reaction with its environment. This process is a worldwide, significant problem because of the economic damage and safety loss it may lead to. The losses originating from corrosion can be categorized as direct and indirect, and the latter includes economic losses caused by plant shutdowns, efficiency reduction, costly maintenance, and contamination of products whose overall impact will ultimately require over-design. The direct losses include the cost of replacing corroded structures, fixing damaged machinery, and substituting some of its components.

Corrosion control can be achieved by recognizing and understanding the mechanisms associated with this process. It is possible to prevent corrosion by using corrosion-resistant materials and protective systems.

The environments to which metals are exposed make them prone to corrosion. A less aggressive environment can be obtained by removing constituents that facilitate corrosion, modifying the temperature, dehumidifying the air, removing dissolved O₂ or solid particles, controlling the pH or adding corrosion inhibitors. The usage of inhibitors is one of the most practical methods for protection against corrosion in acidic, alkaline, saline, and other aggressive environments.

2. Corrosion Inhibitors

Corrosion inhibitors are chemical substances that are added to aggressive environments in small concentrations to decrease the corrosion rate. These substances can react with either a metal surface or its surroundings providing protection to the surface, although it has been observed that corrosion inhibitors generally work by forming an adsorbed film. Corrosion inhibitors are an appropriate option for metal protection when these are exposed to aggressive media, such as, acidic solutions (widely employed for industrial cleaning), oil well acidification, and petrochemical processes ^[1]. Corrosion inhibitors can be introduced into the aggressive environment in a single application or continuously by gradual and controlled additions. The single addition is possible in static systems at low temperature and where friction is negligible. Gradual addition is necessary for systems where variation in flow and temperature degrade the integrity of the protective film formed on the metal surface, either by physisorption or chemisorption. The stability of the corrosion inhibitor films can be compromised by the concentration levels of the inhibitor in the medium. Comparative studies performed to determine inhibition effects are generally performed without shaking. Therefore, the existence of a significant effect of immersion time on the quality of the formed film of an inhibitor is reasonable.

An important number of compounds have been used for the corrosion protection of metals exposed to aggressive media. Their effectiveness is associated to their chemical composition, molecular structure, alkyl chain length (or molecular volume), planarity, presence of lone pairs of electrons in heteroatoms (e.g., S, N, O, P), affinity for the metallic surface, dipole moment, presence of π-electrons (unsaturation or aromatic ring) and energy of frontier molecular orbitals. The efficiency (E%) of corrosion inhibitors is measured by applying the Equation (1) to experimental data obtained by techniques such as weight loss (WL), potentiodynamic polarization (PP), and electrochemical impedance spectroscopy (EIS):

\( E\% = \frac{{\left( {C{R_u} - C{R_i}} \right)}}{{C{R_u}}} \times 100 \). Equation (1)

where CR_u is the corrosion rate of the uninhibited system and CR_i is the rate of the inhibited system.

The mechanisms through which corrosion inhibitors can be bounded to the metal or the metal oxide surface may be physisorption, chemisorption, complexation or precipitation. The film formed by corrosion inhibitors prevents the access of oxygen to the cathode and the diffusion of hydrogen away from it, or simply inhibits metal dissolution (anodic inhibitors). Inhibition efficiency can be altered by modifying the system parameters such as pH, temperature, metal composition, type of inhibitor and molecular structure of the corrosion inhibitor ^[2]. An important factor associated with the corrosion process is surface roughness. The increase in the surface roughness of alloys (magnesium, titanium-based), stainless steels, copper, and aluminum increases the pitting susceptibility and the corrosion rate ^[3].

3. N-Containing Corrosion Inhibitors

An important number of molecules evaluated as corrosion inhibitors in acidic media contain N-atoms and the structural properties that are characteristic of high-performance corrosion inhibitors. Table 1 shows some examples of the N-containing corrosion inhibitors evaluated by different researchers. The Table indicates which corrosion inhibitors have been theoretically analyzed.

Table 1. N-containing corrosion inhibitors

Example	Corrosion Inhibitor	Ef_WL/Ef_PP/Ef_EIS	Ref
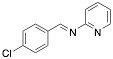	(4-Chloro-benzylidene-pyridine-2-yl-amine)	99.5/99.6/99.6	^[4]
Exp. C. N_CI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 2×10⁻⁴–1×10⁻²M, t: 24 h (WL), T: 25 °C, TA: A
	2,5-bis(2-hydroxyphenyl)-1,3,4-oxadiazole	98.2/94.7/99.1	^[5]
Exp. C. N_CI: 2, Met: mild steel, Media: HCl 1.0 M, 0.5 M H₂SO₄, Co: 20–80 mg•L⁻¹, t: 24 h (WL), 20 h (EIS), T: 30 °C, TA: NA
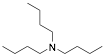	Tributylamine	97.8/-/-	^[6]
Exp. C. N_CI: 23, Met: 13% Cr steel, Media: HCl (15%w/v), Co: 2%w/v inhibitor and 0.6% w/v formaldehyde (used to minimize hydrogen penetration), t: 3 h, T.: 60 °C, TA: A
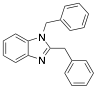	1,2-bisbenzylbenzimidazole	96	^[7]
Exp. C. N_CI: 11, Met: iron, Media: HCl 1.0 M. The analysis technique and the rest of the experimental conditions are not specified. TA: A
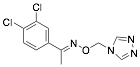	3,4-Dichloro-acetophenone-O-1′-(1′.3′.4′-triazolyl)-metheneoxime (DATM)	92.8/98.7/98.7	^[8]
Exp. C. N_CI: 3, Met: mild steel, Media: HCl 1.0 M, Co:1×10⁻⁵–1×10⁻³M, t: 3 h (WL), 30 min (PP), T: 25 °C, TA: A
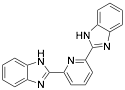	* 2,6-bis-(2-benzimidazolyl) pyridine	-/94–96/97.0	^[9]
Exp. C. N_CI: 4, Met: mild steel, Media: HCl 1.0 M, Co: 0.1–1.0 mM, t: 1–96 h (WL), 45 min (PP), T.: 30 °C, TA: NA
	1-(4-Methyloxyphenylimino)-1-(phenylhydrazono)-propan-2-one	-/95.9/96.2	^[10]
Exp. C. N_CI: 5, Met: mild steel, Media: HCl 1.0 M, Co: 5×10⁻⁶–7.5×10⁻⁵M, t: 30 min, T: 25 °C, TA: NA
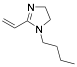	1-Butyl-2-propylene-2-imidazoline	95.1/-/-	^[11]
Exp. C. N_CI: 34, Met: stainless steel, Media: HCl 5%, Co: ≈0.1 M, t: 48 h, T: T_R(room temperature), TA: A
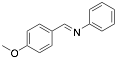	Aniline, N-(p-methoxybenzylidene)	-/94.0/-	^[12]
Exp. C. N_CI: 4, Met: aluminium, Media: HCl 2.0 N, Co: 10⁻⁵–10⁻²M, t:-, T: 30 °C, TA: NA
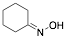	Cyclohexanone oxime	93.9/98.4/95.2	^[13]
Exp. C. N_CI: 3, Met: aluminium, Media: HCl 1.0 M, Co: 0.2–2.0 mM, t: 2 h, T: 20–50 °C, TA: NA
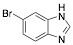	6-Bromo-1H-benzimidazole	-/-/89.4	^[14]
Exp. C. N_CI: 15, Met: carbon steel, Media: HCl 1.0 M, Co:0.1–10 mM, t: 30 min, T: T_R, TA: A
	2-Mercaptobenzimidazole	-/88.7/90.4	^[1]
Exp. C. N_CI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 50–250 ppm, t: 30 min, T: 25 °C, TA: NA
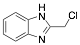	2-Chloromethylbenzimidazole	-/-/69.7	^[15]
Exp. C. N_CI: 6, Met: carbon steel, Media: HCl 1.0 M, Co: 1×10⁻³ M, t: -, T: T_R, TA: A
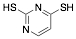	2,4-Dimercaptopyrimidine	43.0/-/-	^[2] ^[16]
Exp. C. N_CI: 14, Met: Aramco iron, Media: HCl 2.0 M, Co: 1×10⁻³ M, t: 1 h, T: 40 °C, TA: A
Simbology: TA: theoretical analysis, A: applied, NA: not applied, Exp. C.: experimental conditions; N_CI: number of corrosion inhibitors, Co: inhibitor concentration, t: exposure time, T: temperature, Ef_WL/Ef_PP/Ef_EIS: corrosion inhibition efficiencies obtained by weight loss (WL), potentiodynamic polarization (PP), and electrochemical impedance spectroscopy (EIS), respectively.

Table 2. S-containing corrosion inhibitors

Example	Corrosion Inhibitor	Ef_WL/Ef_PP/Ef_EIS	Ref
	1-Phenyl thiosemicarbazide	-/100.0/-	^[17]
Exp. C. N_CI: 10, Met: mild steel, Media: H₂SO₄, Co: 1 mMdm⁻³, t: -, T: 30 °C. TA: A
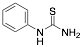	Phenylthiourea (PTU)	-/-/97.2	^[18]
Exp. C. N_CI: 3, Met: mild steel, Media: H₂SO₄ 0.1 M, Co: 1–10 mM, t:1 h, T: T_R, TA: NA
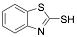	2-Mercaptobenzothiazole	-/97/-	^[19]
Exp. C. N_CI: 1, Met: Steel (API 5L X52), Media: H₂SO₄ 1.0 M, Co: 10^−4-–10⁻³ M, t: 30 min, T: 25 °C, TA: A
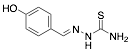	4-Hydroxybenzaldehyde thiosemicarbazone	-/97.0/90.0	^[20]
Exp. C. N_CI: 6, Met: carbon steel, Media: HCl 1.0 M, Co: 10⁻⁴–10⁻²M, t: 30 min, T: 25 °C, TA: NA
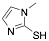	2-Mercapto-1-methylimidazole	90.4 /95.5/-	^[21]
Exp. C. N_CI: 1, Met: carbon steel, Media: HClO₄ 1.0 M, Co: 7.510⁻⁵–2.5 10⁻³ M, t:1 h, T: 30 °C, TA: NA
Simbology: TA: theoretical analysis, A: applied, NA: not applied, Exp. C.: experimental conditions; N_CI: number of corrosion inhibitors, Co: inhibitor concentration, t: exposure time, T: temperature, Ef_WL/Ef_PP/Ef_EIS: corrosion inhibition efficiencies obtained by weight loss (WL), potentiodynamic polarization (PP), and electrochemical impedance spectroscopy (EIS), respectively.

Table 3. O-containing corrosion inhibitors

Example	Corrosion Inhibitor	Ef_WL/Ef_PP/Ef_EIS	Ref
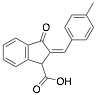	2-(4-Methylbenzylidene)-3-oxo-2,3-dihydro-1H-indene-1-carboxylic acid	92.0/93.9/92.6	^[22]
Exp. C. NCI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 10⁻⁶–10⁻³ M, t: 6 h, T: 30 °C, TA: NA
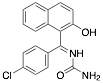	1-((4-Chlorophenyl)(2-hydroxynaphtalen-1-yl)(phenyl) methyl)urea (CPHU)	90/92.0/-	^[23]
Exp. C. NCI: 3, Met: mild steel, Media: H₂SO₄ 0.5 M, Co: 2–10 ppm, t: 24 h (WL) and 30 min (PP), T: 20 °C, TA:A
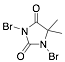	1,3-Dibromo-5,5-dimethylhydantoin	-/89.8/91.4	^[24]
Exp. C. NCI: 6, Met: mild steel, Media: HCl 0.5 M, Co: 10–50 ppm, t: 30 min, T: 30 °C, TA:A
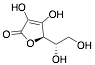	L-ascorbic acid	69.0/-/-	^[25]
Exp. C. NCI: 1, Met: mild steel, Media: H₂SO₄ 0.01 M, Co: 10⁻⁷–10⁻³ M, t: -, T: T_R, TA: NA
Simbology: TA: theoretical analysis, A: applied, NA: not applied, Exp. C.: experimental conditions; N_CI: number of corrosion inhibitors, Co: inhibitor concentration, t: exposure time, T: temperature, Ef_WL/Ef_PP/Ef_EIS: corrosion inhibition efficiencies obtained by weight loss (WL), potentiodynamic polarization (PP), and electrochemical impedance spectroscopy (EIS), respectively.

Table 4. Multi-heteroatom containing corrosion inhibitors

Example	Corrosion Inhibitor	Ef_WL/Ef_PP/Ef_EIS	Ref
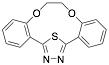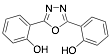
	(2,3,8,9-Dibenzo-4,7-dioxa-13-thia-11,12-diazabicyclo[8.2.1]trideca-10,12-diene (1-MCTH)	97.7/-/-	^[26]
Exp. C. NCI: 5, Met: mild steel, Media: 1.0 M HCl, Co: 110⁻⁶–110⁻⁴ M, t: 24 h (WL), T: 30 °C, TA: A
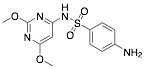	Sulphadimethoxine	93.8/84.0/92.1	^[27]
Exp. C. NCI: 5, Met: mild steel, Media:1.0 M HCl, Co: 1–510⁻⁵ M, t: 30 min, T: 30–50 °C, TA: A
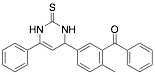	5-Benzoyl-4-tolyl-6-phenyl-1,2,3,4-tetrahydro-2-thioxopyrimidine	-/93.0/93.0	^[28] ^[29]
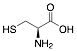Exp. C. NCI: 2, Met: stainless steel, Media:1.0 M HCl, Co:110⁻⁴–5 10⁻³ moldm⁻³, t: 30 min, T: 25 °C. The experimental data were obtained by Caliskan, et al. ^[28]. TA: A
	L-Cysteine	82.2/-/-
Exp. C. NCI: 4, Met: mild steel, Media:0.1 M HCl, Co: 0.1–0.5 gL⁻¹, t: 24, 168 h, T: 30, 60 °C, TA: A
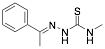	(E)-N-methyl-2-(1-phenylethylidene)hydrazinecarbothioamide PHCARB	80.7/-/-	^[30]
Exp. C. NCI: 4, Met: mild steel, Media:0.1 M HCl, Co: 1–510⁻⁴ M, t: 168 h, T: 30 °C, TA: A
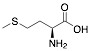	Methionine	72.7/84.6/85.8
Exp. C. NCI: 16, Met: Armco iron, Media: HCl 1.0 M, Co: 10⁻³ M, et: 6 h (WL), 10 y 30 min (PP), T: 35 °C, TA: A
Simbology: TA: theoretical analysis, A: applied, NA: not applied, Exp. C.: experimental conditions; NCI: number of corrosion inhibitors. Co: inhibitor concentration, t: exposure time, T: temperature, Ef_WL/Ef_PP/Ef_EIS: corrosion inhibition efficiencies obtained by weight loss (WL), potentiodynamic polarization (PP), and electrochemical impedance spectroscopy (EIS), respectively.

Table 5. Examples of descriptors used in the theoretical analysis of corrosion inhibitors.

Quantum Descriptor	Symbol	Description	Reference
Energy of the highest occupied molecular orbital	E_HOMO	Associated with the electron-donating ability of a molecule.	^[4]
Energy of the lowest unoccupied molecular orbital	E_LUMO	Indicates the ability of the molecule to accept electrons.	^[21]
Ionization potential	IP	It is a descriptor of the chemical reactivity of atoms and molecules. IP is the minimum energy required to remove an electron from an atom.	^[29]
Electron affinity	A	It is a property that determines how susceptible a molecule is towards the attack of a nucleophile.	^[31]
Dipole moment	_μD	The dipole moment is considered a measure of the stability of the formed complex on a metal surface. It is an indicator of the asymmetry in the molecular charge distribution. It is related to the hydrophobic character of the molecules.	^[23] ^[32] ^[33]
Energy gap	ΔE	ΔE= E_{HOMO −}E_LUMO It has been mentioned that the successful adsorption and proper efficiency of an inhibitor have been characterized by a high E_HOMO, a low E_LUMO_,and a small energy gap. The lower the ΔE is, the higher the stability of the metal-inhibitor interaction.	^[9] ^[32] ^[34]
Fraction of electron transferred	ΔN	If ΔN > 3.6, the inhibition efficiency increases	^[9]
Global hardness	η	It is a parameter associated with the resistance of an atom to transfer its charge.	^[9]
Softness	σ	The σ shows the reactivity of the inhibitor molecules in terms of charge transfer.	^[9]
Electronegativity	χ	The electronegativity measures the power of a group of atoms to attract electrons towards itself.	^[9]
Electrophilicity index	ω	It is a reactivity descriptor that allows the quantitative classification of the global electrophilic nature of a molecule. This descriptor has been proposed as a measure of energy lowering due to maximal electron flow between donor and acceptor.	^[8]
Electrodonating power	ω^-	A descriptor associated with the ability of a species to donate electrons.	^[35]
Electroaccepting power	ω⁺	A descriptor associated with the ability of a species to accept electrons.	^[35]
Dipole polarizability	α	α is a measure of the mean polarizability. Higher values of α enable a strong adsorption process.	^[8]
Fukui functions	f_k⁺, f_k ^-	These functions indicate the part of the molecule where nucleophilic, electrophilic, and radical attack is most likely to occur.	^[31]
Partition coefficient	Log P	Log P is a hydrophobic parameter of a molecule.	^[36]

Table 6. Examples of mathematical models generated for corrosion analysis.

Molecules Evaluated	Theoretical Calculation	Mathematical Model	R²	Ref.
Schiff base	AM1 semi-empirical method	\( {\small I{E_{exp}}\left( \% \right) = 2.084{E_{HOMO}} - 3.041{E_{LUMO}} + 115.772 } \)	1.00	^[4]
Schiff base	AM1 semi-empirical method	\( {\small IE_{Theor}=\frac{\left(-604.90E_{HOMO}+5864.86E_{LUMO}+1190.06\mu_D-642.67\right)C}{\left[1+\left(-604.90E_{HOMO}+5864.86E_{LUMO}+1190.06\mu_D-642.67\right)C\right]} } \)	0.98	^[4]
Amines, thioureas, acetylenic alcohols	AM1 methodology was used for most descriptors, PC model provided the volume calculations	\( {\small \begin{matrix}lnK_{ads}=-0.93N-7.64P+6.74C-2.27C_{12}+0.94C_{13}-1.06C_1\\-7.22C_2-2.17E_{HOMO}-1.17DP+7.45V-1.15A_1\\-1.81A_2+7.12NCS-1.869NOH-1.085NCR\\\end{matrix} } \)	0.98	^[6]
		\( {\small lnK_{ads}=1.52M-0.79P+0.53C_{12}+0.80NT-0.66NOH } \)	0.86
		\( {\small \begin{array}{*{20}{c}} {{\rm{ ln}}{{\rm{K}}_{{\rm{ads}}}}{\rm{ = }}}&{ - 2.688 \times {{10}^{ - 2}}{A_1} + 0.115{A_2} + 4.530 \times {{10}^{ - 2}}{A_3} + 8.762 \times {{10}^{ - 2}}NB - 1.305 \times {{10}^{ - 2}}NC}\\ {}&{ + 0.102NCS - 4.518 \times {{10}^{ - 2}}NT - 5.172 \times {{10}^{ - 2}}NOH - 1.099 \times {{10}^{ - 3}}NCR + 4.996 \times {{10}^{ - 2}}NR}\\ {}&{ - 6.338 \times {{10}^{ - 2}}N - 0.114ED + 0.184M + 0.180P - 6.838 \times {{10}^{ - 2}}C + 8.092 \times {{10}^{ - 2}}{C_{12}}}\\ {}&{ - 4.783 \times {{10}^{ - 2}}{C_{13}} - 1.130 \times {{10}^{ - 2}}{C_{14}} - 0.167{C_1} - 0.152{C_2} - 0.122{E_{HOMO}}}\\ {}&{{\rm{ - 7.838}} \times {\rm{1}}{{\rm{0}}^{ - 2}}{{\rm{E}}_{{\rm{LUMO}}}}{\rm{ - 7.004}} \times {\rm{1}}{{\rm{0}}^{ - 3}}\Delta {\rm{E + 0.109}}\mu {\rm{ + 0.141V}}} \end{array} } \)	0.85
Triazole derivatives	Density Functional Theory (DFT), B3LYP/6-31G	\( {\small IE_{Theor}=\frac{\left(18.38E_{HOMO}-7.28E_{LUMO}-0.012V+123.36\right)C}{\left[1+\left(18.38E_{HOMO}-7.28E_{LUMO}-0.012V+123.36\right)C\right]} } \) Derived QSAR equation in gas phase	0.94	^[8]
Triazole derivatives	Density Functional Theory (DFT), B3LYP/6-31G	\( {\small IE_{Theor}=\frac{\left(-2.19E_{HOMO}-1.24E_{LUMO}-0.014V-10.94\right)C}{\left[1+\left(-2.19E_{HOMO}-1.24E_{LUMO}-0.014V-10.94\right)C\right]} } \) Derived QSAR equation in aqueous phase	0.95	^[8]
Imidazole derivatives	Restricted Hartree–Fock level (RHF) using MINDO/3, MNDO, PM3 and AM1 semi-empirical SCF-MO methods.	\( {\small I{E_{exp}}\left( \% \right) = 1174.95 + 214.612{E_{HOMO}} - 16.793{E_{LUMO}} } \) Gas phase (series 1)	0.90	^[7]
		\( {\small I{E_{exp}}\left( \% \right) = 517.7 + 53.8{E_{HOMO}} - 1.97{E_{LUMO}} } \) Aqueous phase (series 1)	0.82
		\( {\small I{E_{exp}}\left( \% \right) = 2420.86 + 295.67{E_{HOMO}} - 30.08{E_{LUMO}} } \) Gas phase (series 2)	0.97
		\( {\small I{E_{exp}}\left( \% \right) = 601.53 + 63.07{E_{HOMO}} - 1.405{E_{LUMO}} } \) Aqueous phase (series 2)	0.99
Imidazole and benzimidazole derivatives	---	\( {\small I{E_{exp}}\left( \% \right) = 38.47 + 20.21n\left( N \right) - 7.98N\left( {O + N{H_2}} \right) + 14.94{\eta ^ + } - 17.93{\eta ^ - } } \)	0.97	^[11]
Indole derivatives	DFT, B3LYP functional and 6-31G(2d,2p) basis	\( {\small R_{ct}=150+\left(-359539E_{HOMO}+1585825E_{LUMO}\right)C } \)	0.97	^[26]
Indole derivatives	DFT, B3LYP functional and 6-31G(2d,2p) basis	\( {\small R_{ct}=150+\left(-402535E_{HOMO}+960146E_{LUMO}\right)C } \)	0.97	^[26]
Imidazole and benzimidazole derivatives	DFT: PBE/6-311++G **	\( {\small {E_{exp}}\left( \% \right) = 5130.95 - 32.03\chi + 533.4b{q^{ISO}} + 0.37V + 1433.78{q_{N1}} } \)	0.92	^[37]
Imidazole, benzimidazole and pyridine derivatives	DFT: PBE/B3LYP/M06, using the orbital basis 6-31G* and 6-311++G**	\( {\small I{E_{exp}}\left( \% \right) = 92.965 + 0.152V + 35.337{\omega ^ - } + 3.592b{q_{ANS}} } \)	0.75	^[14]
Pyrimidine derivatives	DFT BLYP/DNP	\( {\small I{E_{exp}}\left( \% \right) = - 4.324\mu - 46.527{\rm{\Delta }}E + 376.48{q_{N1}} } \)	0.98	^[16]
Thiosemicarbazides	PM3 and MNDO method.	\( {\small IE_{Theor}=\frac{\left(-6.7E_{HOMO}-5.9E_{LUMO}-3.5\mu-43.7\right)C}{\left[1+\left(-6.7E_{HOMO}-5.9E_{LUMO}-3.5\mu-43.7\right)C\right]}\times100 } \)	0.84
Thiosemicarbazides	PM3 and MNDO method.	\( {\small IE_{Theor}=\frac{\left(227.2+23.5E_{HOMO}-3.8\mu\right)C}{\left[1+\left(227.2+23.5E_{HOMO}-3.8\mu\right)C\right]}\times100 } \)	0.92
Thiosemicarbazides/ Thiosemicarbazones	Data obtained from literature	\( {\small IE_{exp}=\frac{e^{-2.5219E_{HOMO}-0.5119\mu_D-18.1761}C}{\left(1+e^{-2.5219E_{HOMO}-0.5119\mu_D-18.1761}C\right)} } \)	0.89	^[17]
Thiosemicarbazides/ Thiosemicarbazones	Data obtained from literature	\( {\small {\rm{I}}{{\rm{E}}_{{\rm{exp}}}}{\rm{ = }}\frac{{{{\rm{e}}^{{\rm{263.12}}\Delta {\rm{E - 17.26}}\Delta {\rm{E2 - 999.22}}}}{\rm{C}}}}{{{\rm{1 + }}{{\rm{e}}^{{\rm{263.12}}\Delta {\rm{E - 17.26}}\Delta {\rm{E2 - 999.22}}}}}} } \)	0.88	^[17]
2-Mercaptobenzothiazole	DFT: B3LYP/6-31+G*	\( {\small I{E_{Theor}} = \frac{{\left( {2.23{E_{HOMO}} - 8.37{E_{LUMO}} + 5.47\Delta E + 1.76\Delta N + 6.47\mu + 119.8V + 2.07} \right)C}}{{\left[ {1 + \left( {2.23{E_{HOMO}} - 8.37{E_{LUMO}} + 5.47\Delta E + 1.76\Delta N + 6.47\mu + 119.8V + 2.07} \right)C} \right]}} \times 100 } \)	0.96	^[19]
Urea derivatives	DFT: B3LYP/6-31G	\( {\small ∆E=-0.0024IEexp-4.3145} \)	0.95	^[23]
Urea derivatives	DFT: B3LYP/6-31G	\( {\small ∆{E=-0.0024IEexp-4.3145_{HOMO}} = - 0.0107I{E_{\exp }} - 4.88596 } \)	0.93	^[23]
Hydantoin derivatives	DFT: B3LYP/6-31G+(d,p)	\( {\small ∆IE=-0.0024IEexp-4.3145_{Theor}=129.054-0.181Mwt-6.550∆E-174.884∆N+0.484BE } \)	1.00	^[24]
Hydantoin derivatives	DFT: B3LYP/6-31G+(d,p)	\( {\small ∆I{E=-0.0024IEexp-4.3145} \_{Theor}} = \frac{{\left( {9.1 \times {{10}^{13}}Mwt + 4.9 \times {{10}^{14}}\Delta N + 9.7 \times {{10}^{13}}\Delta E + 2.4 \times {{10}^{13}}BE - 5.9 \times {{10}^{13}}} \right)}}{{\left( {1 + 1.8 \times {{10}^{13}}Mwt + 1.8 \times {{10}^{16}}\Delta N + 8.1 \times {{10}^{14}}\Delta E - 1.2 \times {{10}^{13}}BE - 7.2 \times {{10}^{15}}} \right)}} } \)	0.99	^[24]
Polyether compounds	DFT B3LYP/6-31G(d,p)	\( {\small ∆ER_t=-0.0024IEexp-4.31455+\left(2.710^7E_{HOMO}-7.610^7E_{LUMO}+3.910^6\mu\right)C } \)	0.81	^[26]
Sulphonamide derivatives	DFT: B3LYP/6-311+G(d,p)	\( {\small ∆I{E=-0.0024IEexp-4.3145} \_{\exp }}\left( \% \right) = \frac{{\left( {2.47\omega + 8.56 \times {{10}^{ - 2}}{E_{LUMO}} - 5.27 \times {{10}^{ - 2}}\mu + 6.20\eta - 4.11 \times {{10}^{ - 2}}LogP - 21.81} \right) * 5000}}{{\left( {1 + \left( {2.47\omega + 8.56 \times {{10}^{ - 2}}{E_{LUMO}} - 5.27 \times {{10}^{ - 2}}\mu + 6.20\eta - 4.11 \times {{10}^{ - 2}}LogP - 21.81} \right) * 50} \right)}} } \)	1.00	^[27]
Sulphonamide derivatives	DFT: B3LYP/6-311+G(d,p)	\( {\small ∆I{E=-0.0024IEexp-4.3145} \_{\exp }}\left( \% \right) = \frac{{\left( { - 1.44\Delta E + 3.48{E_{LUMO}} - 3.50{E_{HOMO}} + 1.07\eta + 1.75{\omega ^ + } - 17.85} \right)5000}}{{\left( {1 + \left( { - 1.44\Delta E + 3.48{E_{LUMO}} - 3.50{E_{HOMO}} + 1.07\eta + 1.75{\omega ^ + } - 17.85} \right)50} \right)}} } \)	0.99	^[27]
	Pyrimidine compounds	B3LYP/6-311++G(d,p)	\( {\small ∆E=-0.0024IEexp-4.3145} \)

References

J. Aljourani; K. Raeissi; M.A. Golozar; Benzimidazole and its derivatives as corrosion inhibitors for mild steel in 1M HCl solution. Corrosion Science 2009, 51, 1836-1843, 10.1016/j.corsci.2009.05.011.
István Lukovits; E. Kálmán; F. Zucchi; Corrosion Inhibitors—Correlation between Electronic Structure and Efficiency. Corrosion 2001, 57, 3-8, 10.5006/1.3290328.
A. S. Toloei; V. Stoilov; D. O. Northwood; Simultaneous effect of surface roughness and passivity on corrosion resistance of metals. Materials Characterisation VII 2015, 90, 355-367, 10.2495/mc150321.
H. Ashassi-Sorkhabi; B. Shaabani; D. Seifzadeh; Corrosion inhibition of mild steel by some schiff base compounds in hydrochloric acid. Applied Surface Science 2005, 239, 154-164, 10.1016/j.apsusc.2004.05.143.
F. Bentiss; M. Traisnel; M. Lagrenee; The substituted 1,3,4-oxadiazoles: a new class of corrosion inhibitors of mild steel in acidic media. Corrosion Science 2000, 42, 127-146, 10.1016/s0010-938x(99)00049-9.
S. P. Cardoso; J. A. C. P. Gomes; L. E. P. Borges; E. Hollauer; Predictive QSPR analysis of corrosion inhibitors for super 13% Cr steel in hydrochloric acid. Brazilian Journal of Chemical Engineering 2007, 24, 547-559, 10.1590/s0104-66322007000400008.
G Bereket; E Hür; C Öğretir; Quantum chemical studies on some imidazole derivatives as corrosion inhibitors for iron in acidic medium. Journal of Molecular Structure: THEOCHEM 2002, 578, 79-88, 10.1016/s0166-1280(01)00684-4.
Lei Guo; Shanhong Zhu; Shengtao Zhang; Qiao He; Weihua Li; Theoretical studies of three triazole derivatives as corrosion inhibitors for mild steel in acidic medium. Corrosion Science 2014, 87, 366-375, 10.1016/j.corsci.2014.06.040.
Alokdut Dutta; Sourav Kr. Saha; Priyabrata Banerjee; Dipankar Sukul; Correlating electronic structure with corrosion inhibition potentiality of some bis-benzimidazole derivatives for mild steel in hydrochloric acid: Combined experimental and theoretical studies. Corrosion Science 2015, 98, 541-550, 10.1016/j.corsci.2015.05.065.
Hanane Hamani; Tahar Douadi; Mousa Al-Noaimi; Saifi Issaadi; Djamel Daoud; Salah Chafaa; Electrochemical and quantum chemical studies of some azomethine compounds as corrosion inhibitors for mild steel in 1M hydrochloric acid. Corrosion Science 2014, 88, 234-245, 10.1016/j.corsci.2014.07.044.
Mohammad Hossein Keshavarz; Karim Esmaeilpour; Ahmad Nozad Golikand; Zeinab Shirazi; Simple Approach to Predict Corrosion Inhibition Efficiency of Imidazole and Benzimidazole Derivatives as well as Linear Organic Compounds Containing Several Polar Functional Groups. Zeitschrift für anorganische und allgemeine Chemie 2016, 642, 906-913, 10.1002/zaac.201600230.
Gamal K. Gomma; Mostafa H. Wahdan; Schiff bases as corrosion inhibitors for aluminium in hydrochloric acid solution. Materials Chemistry and Physics 1995, 39, 209-213, 10.1016/0254-0584(94)01436-k.
Xianghong Li; Shuduan Deng; Xiaoguang Xie; Experimental and theoretical study on corrosion inhibition of oxime compounds for aluminium in HCl solution. Corrosion Science 2014, 81, 162-175, 10.1016/j.corsci.2013.12.021.
Evelin Gutiérrez; José G. Alvarado-Rodríguez; Julián Cruz-Borbolla; Pandiyan Thangarasu; Development of a predictive model for corrosion inhibition of carbon steel by imidazole and benzimidazole derivatives. Corrosion Science 2016, 108, 23-35, 10.1016/j.corsci.2016.02.036.
Rosa L. Camacho-Mendoza; Evelin Gutiérrez; Edmundo G. Percástegui; Eliazar Aquino-Torres; Julián Cruz-Borbolla; José A. Rodríguez-Ávila; José G. Alvarado-Rodríguez; Oscar Olvera-Neria; Pandiyan Thangarasu; José L. Medina-Franco; et al. Density Functional Theory and Electrochemical Studies: Structure–Efficiency Relationship on Corrosion Inhibition. Journal of Chemical Information and Modeling 2015, 55, 2391-2402, 10.1021/acs.jcim.5b00385.
K.F. Khaled; Modeling corrosion inhibition of iron in acid medium by genetic function approximation method: A QSAR model. Corrosion Science 2011, 53, 3457-3465, 10.1016/j.corsci.2011.01.035.
István Lukovits; Abdul Shaban; Erika Kálmán; Thiosemicarbazides and thiosemicarbazones: non-linear quantitative structure–efficiency model of corrosion inhibition. Electrochimica Acta 2005, 50, 4128-4133, 10.1016/j.electacta.2005.01.029.
M Özcan; I Dehri; M Erbil; Organic sulphur-containing compounds as corrosion inhibitors for mild steel in acidic media: correlation between inhibition efficiency and chemical structure. Applied Surface Science 2004, 236, 155-164, 10.1016/j.apsusc.2004.04.017.
Majid Gholami; Iman Danaee; Mohammad Hosein Maddahy; Mehdi Rashvandavei; Correlated ab Initio and Electroanalytical Study on Inhibition Behavior of 2-Mercaptobenzothiazole and Its Thiole–Thione Tautomerism Effect for the Corrosion of Steel (API 5L X52) in Sulphuric Acid Solution. Industrial & Engineering Chemistry Research 2013, 52, 14875-14889, 10.1021/ie402108g.
Carla Marins Goulart; Andressa Esteves-Souza; Carlos Alberto Martinez-Huitle; Ciro José Ferreira Rodrigues; Maria Aparecida Medeiros Maciel; Aurea Echevarria; Experimental and theoretical evaluation of semicarbazones and thiosemicarbazones as organic corrosion inhibitors. Corrosion Science 2013, 67, 281-291, 10.1016/j.corsci.2012.10.029.
Omar Benali; Lahcene Larabi; M. Traisnel; Leon Gengembre; Yahia Harek; Electrochemical, theoretical and XPS studies of 2-mercapto-1-methylimidazole adsorption on carbon steel in 1M HClO4. Applied Surface Science 2007, 253, 6130-6139, 10.1016/j.apsusc.2007.01.075.
A. Saady; F. El-Hajjaji; M. Taleb; K. Ismaily Alaoui; A. El Biache; A. Mahfoud; G. Alhouari; B. Hammouti; D.S. Chauhan; M.A. Quraishi; et al. Experimental and theoretical tools for corrosion inhibition study of mild steel in aqueous hydrochloric acid solution by new indanones derivatives. Materials Discovery 2018, 12, 30-42, 10.1016/j.md.2018.11.001.
M.J. Bahrami; S.M.A. Hosseini; P. Pilvar; Experimental and theoretical investigation of organic compounds as inhibitors for mild steel corrosion in sulfuric acid medium. Corrosion Science 2010, 52, 2793-2803, 10.1016/j.corsci.2010.04.024.
Lukman O. Olasunkanmi; Bryan P. Moloto; Ime B. Obot; Eno E. Ebenso; Anticorrosion studies of some hydantoin derivatives for mild steel in 0.5 M HCl solution: Experimental, quantum chemical, Monte Carlo simulations and QSAR studies. Journal of Molecular Liquids 2018, 252, 62-74, 10.1016/j.molliq.2017.11.169.
E.S Ferreira; C Giacomelli; A Spinelli; Evaluation of the inhibitor effect of l-ascorbic acid on the corrosion of mild steel. Materials Chemistry and Physics 2004, 83, 129-134, 10.1016/j.matchemphys.2003.09.020.
M. Lebrini; M. Lagrenée; H. Vezin; M. Traisnel; F. Bentiss; Experimental and theoretical study for corrosion inhibition of mild steel in normal hydrochloric acid solution by some new macrocyclic polyether compounds. Corrosion Science 2007, 49, 2254-2269, 10.1016/j.corsci.2006.10.029.
Lutendo C. Murulana; Mwadham M. Kabanda; Eno E. Ebenso; Investigation of the adsorption characteristics of some selected sulphonamide derivatives as corrosion inhibitors at mild steel/hydrochloric acid interface: Experimental, quantum chemical and QSAR studies. Journal of Molecular Liquids 2016, 215, 763-779, 10.1016/j.molliq.2015.12.095.
N. Caliskan; E. Akbas; Corrosion inhibition of austenitic stainless steel by some pyrimidine compounds in hydrochloric acid. Materials and Corrosion 2012, 63, 231-237, 10.1002/maco.201005788.
Fahimeh Shojaie; Nasser Mirzai-Baghini; Molecular dynamics and density functional theory study on the corrosion inhibition of austenitic stainless steel in hydrochloric acid by two pyrimidine compounds. International Journal of Industrial Chemistry 2015, 6, 297-310, 10.1007/s40090-015-0052-x.
Nnabuk O. Eddy; Benedict I. Ita; QSAR, DFT and quantum chemical studies on the inhibition potentials of some carbozones for the corrosion of mild steel in HCl. Journal of Molecular Modeling 2011, 17, 359-376, 10.1007/s00894-010-0731-7.
M. M. Aboelnga; M. K. Awad; J. W. Gauld; M. R. Mustafa; An assessment to evaluate the validity of different methods for the description of some corrosion inhibitors. Journal of Molecular Modeling 2014, 20, 1-17, 10.1007/s00894-014-2422-2.
Guo Gao; Chenghao Liang; Electrochemical and DFT studies of β-amino-alcohols as corrosion inhibitors for brass. Electrochimica Acta 2007, 52, 4554-4559, 10.1016/j.electacta.2006.12.058.
Fatma Kandemirli; Seda Sagdinc; Theoretical study of corrosion inhibition of amides and thiosemicarbazones. Corrosion Science 2007, 49, 2118-2130, 10.1016/j.corsci.2006.10.026.
El Sayed H. El Ashry; Ahmed El Nemr; Samy A. Essawy; Safaa Ragab; Corrosion inhibitors part V: QSAR of benzimidazole and 2-substituted derivatives as corrosion inhibitors by using the quantum chemical parameters. Progress in Organic Coatings 2008, 61, 11-20, 10.1016/j.porgcoat.2007.08.009.
José L. Gázquez; Andrés Cedillo; Alberto Vela; Electrodonating and Electroaccepting Powers. The Journal of Physical Chemistry A 2007, 111, 1966-1970, 10.1021/jp065459f.
I. Lukovits; Abdul Shaban; E. Kálmán; Corrosion Inhibitors: Quantitative Structure–Activity Relationships. Russian Journal of Electrochemistry 2003, 39, 177-181, 10.1023/A:1022313126231.
Rosa L. Camacho-Mendoza; Evelin Gutiérrez-Moreno; Edmundo Guzmán-Percástegui; Eliazar Aquino-Torres; Julián Cruz-Borbolla; José A. Rodríguez-Ávila; José G. Alvarado-Rodríguez; Oscar Olvera-Neria; Pandiyan Thangarasu; José L. Medina-Franco; et al. Density Functional Theory and Electrochemical Studies: Structure–Efficiency Relationship on Corrosion Inhibition. Journal of Chemical Information and Modeling 2015, 55, 2391-2402, 10.1021/acs.jcim.5b00385.
Rosa L. Camacho-Mendoza; Evelin Gutiérrez-Moreno; Edmundo Guzmán-Percástegui; Eliazar Aquino-Torres; Julián Cruz-Borbolla; José A. Rodríguez-Ávila; José G. Alvarado-Rodríguez; Oscar Olvera-Neria; Pandiyan Thangarasu; José L. Medina-Franco; et al. Density Functional Theory and Electrochemical Studies: Structure–Efficiency Relationship on Corrosion Inhibition. Journal of Chemical Information and Modeling 2015, 55, 2391-2402, 10.1021/acs.jcim.5b00385.

1. Introduction

2. Corrosion Inhibitors

3. N-Containing Corrosion Inhibitors

Table 1. N-containing corrosion inhibitors

Example

Corrosion Inhibitor

EfWL/EfPP/EfEIS

Ref

(4-Chloro-benzylidene-pyridine-2-yl-amine)

99.5/99.6/99.6

Exp. C. NCI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 2×10−4–1×10−2 M, t: 24 h (WL), T: 25 °C, TA: A

2,5-bis(2-hydroxyphenyl)-1,3,4-oxadiazole

98.2/94.7/99.1

Exp. C. NCI: 2, Met: mild steel, Media: HCl 1.0 M, 0.5 M H2SO4, Co: 20–80 mg•L−1, t: 24 h (WL), 20 h (EIS), T: 30 °C, TA: NA

Tributylamine

97.8/-/-

Exp. C. NCI: 23, Met: 13% Cr steel, Media: HCl (15%w/v), Co: 2%w/v inhibitor and 0.6% w/v formaldehyde (used to minimize hydrogen penetration), t: 3 h, T.: 60 °C, TA: A

1,2-bisbenzylbenzimidazole

96

Exp. C. NCI: 11, Met: iron, Media: HCl 1.0 M. The analysis technique and the rest of the experimental conditions are not specified. TA: A

3,4-Dichloro-acetophenone-O-1′-(1′.3′.4′-triazolyl)-metheneoxime (DATM)

92.8/98.7/98.7

Exp. C. NCI: 3, Met: mild steel, Media: HCl 1.0 M, Co:1×10−5–1×10−3 M, t: 3 h (WL), 30 min (PP), T: 25 °C, TA: A

* 2,6-bis-(2-benzimidazolyl) pyridine

-/94–96/97.0

Exp. C. NCI: 4, Met: mild steel, Media: HCl 1.0 M, Co: 0.1–1.0 mM, t: 1–96 h (WL), 45 min (PP), T.: 30 °C, TA: NA

1-(4-Methyloxyphenylimino)-1-(phenylhydrazono)-propan-2-one

-/95.9/96.2

Exp. C. NCI: 5, Met: mild steel, Media: HCl 1.0 M, Co: 5×10−6–7.5×10−5 M, t: 30 min, T: 25 °C, TA: NA

1-Butyl-2-propylene-2-imidazoline

95.1/-/-

Exp. C. NCI: 34, Met: stainless steel, Media: HCl 5%, Co: ≈0.1 M, t: 48 h, T: TR (room temperature), TA: A

Aniline, N-(p-methoxybenzylidene)

-/94.0/-

Exp. C. NCI: 4, Met: aluminium, Media: HCl 2.0 N, Co: 10−5–10−2 M, t:-, T: 30 °C, TA: NA

Cyclohexanone oxime

93.9/98.4/95.2

Exp. C. NCI: 3, Met: aluminium, Media: HCl 1.0 M, Co: 0.2–2.0 mM, t: 2 h, T: 20–50 °C, TA: NA

6-Bromo-1H-benzimidazole

-/-/89.4

Exp. C. NCI: 15, Met: carbon steel, Media: HCl 1.0 M, Co:0.1–10 mM, t: 30 min, T: TR, TA: A

2-Mercaptobenzimidazole

-/88.7/90.4

Exp. C. NCI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 50–250 ppm, t: 30 min, T: 25 °C, TA: NA

2-Chloromethylbenzimidazole

-/-/69.7

Exp. C. NCI: 6, Met: carbon steel, Media: HCl 1.0 M, Co: 1×10−3 M, t: -, T: TR, TA: A

2,4-Dimercaptopyrimidine

43.0/-/-

Exp. C. NCI: 14, Met: Aramco iron, Media: HCl 2.0 M, Co: 1×10−3 M, t: 1 h, T: 40 °C, TA: A

Table 2. S-containing corrosion inhibitors

Example

Corrosion Inhibitor

EfWL/EfPP/EfEIS

Ref

1-Phenyl thiosemicarbazide

-/100.0/-

Exp. C. NCI: 10, Met: mild steel, Media: H2SO4, Co: 1 mMdm−3, t: -, T: 30 °C. TA: A

Phenylthiourea (PTU)

-/-/97.2

Exp. C. NCI: 3, Met: mild steel, Media: H2SO4 0.1 M, Co: 1–10 mM, t:1 h, T: TR, TA: NA

2-Mercaptobenzothiazole

-/97/-

Exp. C. NCI: 1, Met: Steel (API 5L X52), Media: H2SO4 1.0 M, Co: 10−4-–10−3 M, t: 30 min, T: 25 °C, TA: A

4-Hydroxybenzaldehyde thiosemicarbazone

-/97.0/90.0

Exp. C. NCI: 6, Met: carbon steel, Media: HCl 1.0 M, Co: 10−4–10−2 M, t: 30 min, T: 25 °C, TA: NA

2-Mercapto-1-methylimidazole

90.4 /95.5/-

Exp. C. NCI: 1, Met: carbon steel, Media: HClO4 1.0 M, Co: 7.510−5–2.5 10−3 M, t:1 h, T: 30 °C, TA: NA

Table 3. O-containing corrosion inhibitors

Example

Corrosion Inhibitor

EfWL/EfPP/EfEIS

Ref

2-(4-Methylbenzylidene)-3-oxo-2,3-dihydro-1H-indene-1-carboxylic acid

92.0/93.9/92.6

Exp. C. NCI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 10−6–10−3 M, t: 6 h, T: 30 °C, TA: NA

1-((4-Chlorophenyl)(2-hydroxynaphtalen-1-yl)(phenyl) methyl)urea (CPHU)

90/92.0/-

Ef_WL/Ef_PP/Ef_EIS

Exp. C. N_CI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 2×10⁻⁴–1×10⁻²M, t: 24 h (WL), T: 25 °C, TA: A

Exp. C. N_CI: 2, Met: mild steel, Media: HCl 1.0 M, 0.5 M H₂SO₄, Co: 20–80 mg•L⁻¹, t: 24 h (WL), 20 h (EIS), T: 30 °C, TA: NA

Exp. C. N_CI: 23, Met: 13% Cr steel, Media: HCl (15%w/v), Co: 2%w/v inhibitor and 0.6% w/v formaldehyde (used to minimize hydrogen penetration), t: 3 h, T.: 60 °C, TA: A

Exp. C. N_CI: 11, Met: iron, Media: HCl 1.0 M. The analysis technique and the rest of the experimental conditions are not specified. TA: A

Exp. C. N_CI: 3, Met: mild steel, Media: HCl 1.0 M, Co:1×10⁻⁵–1×10⁻³M, t: 3 h (WL), 30 min (PP), T: 25 °C, TA: A

Exp. C. N_CI: 4, Met: mild steel, Media: HCl 1.0 M, Co: 0.1–1.0 mM, t: 1–96 h (WL), 45 min (PP), T.: 30 °C, TA: NA

Exp. C. N_CI: 5, Met: mild steel, Media: HCl 1.0 M, Co: 5×10⁻⁶–7.5×10⁻⁵M, t: 30 min, T: 25 °C, TA: NA

Exp. C. N_CI: 34, Met: stainless steel, Media: HCl 5%, Co: ≈0.1 M, t: 48 h, T: T_R(room temperature), TA: A

Exp. C. N_CI: 4, Met: aluminium, Media: HCl 2.0 N, Co: 10⁻⁵–10⁻²M, t:-, T: 30 °C, TA: NA

Exp. C. N_CI: 3, Met: aluminium, Media: HCl 1.0 M, Co: 0.2–2.0 mM, t: 2 h, T: 20–50 °C, TA: NA

Exp. C. N_CI: 15, Met: carbon steel, Media: HCl 1.0 M, Co:0.1–10 mM, t: 30 min, T: T_R, TA: A

Exp. C. N_CI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 50–250 ppm, t: 30 min, T: 25 °C, TA: NA

Exp. C. N_CI: 6, Met: carbon steel, Media: HCl 1.0 M, Co: 1×10⁻³ M, t: -, T: T_R, TA: A

Exp. C. N_CI: 14, Met: Aramco iron, Media: HCl 2.0 M, Co: 1×10⁻³ M, t: 1 h, T: 40 °C, TA: A

Ef_WL/Ef_PP/Ef_EIS

Exp. C. N_CI: 10, Met: mild steel, Media: H₂SO₄, Co: 1 mMdm⁻³, t: -, T: 30 °C. TA: A

Exp. C. N_CI: 3, Met: mild steel, Media: H₂SO₄ 0.1 M, Co: 1–10 mM, t:1 h, T: T_R, TA: NA

Exp. C. N_CI: 1, Met: Steel (API 5L X52), Media: H₂SO₄ 1.0 M, Co: 10^−4-–10⁻³ M, t: 30 min, T: 25 °C, TA: A

Exp. C. N_CI: 6, Met: carbon steel, Media: HCl 1.0 M, Co: 10⁻⁴–10⁻²M, t: 30 min, T: 25 °C, TA: NA

Exp. C. N_CI: 1, Met: carbon steel, Media: HClO₄ 1.0 M, Co: 7.510⁻⁵–2.5 10⁻³ M, t:1 h, T: 30 °C, TA: NA

Ef_WL/Ef_PP/Ef_EIS

Exp. C. NCI: 3, Met: mild steel, Media: HCl 1.0 M, Co: 10⁻⁶–10⁻³ M, t: 6 h, T: 30 °C, TA: NA

Exp. C. NCI: 3, Met: mild steel, Media: H₂SO₄ 0.5 M, Co: 2–10 ppm, t: 24 h (WL) and 30 min (PP), T: 20 °C, TA:A

Exp. C. NCI: 1, Met: mild steel, Media: H₂SO₄ 0.01 M, Co: 10⁻⁷–10⁻³ M, t: -, T: T_R, TA: NA

Ef_WL/Ef_PP/Ef_EIS

Exp. C. NCI: 5, Met: mild steel, Media: 1.0 M HCl, Co: 110⁻⁶–110⁻⁴ M, t: 24 h (WL), T: 30 °C, TA: A

Exp. C. NCI: 5, Met: mild steel, Media:1.0 M HCl, Co: 1–510⁻⁵ M, t: 30 min, T: 30–50 °C, TA: A

Exp. C. NCI: 2, Met: stainless steel, Media:1.0 M HCl, Co:110⁻⁴–5 10⁻³ moldm⁻³, t: 30 min, T: 25 °C. The experimental data were obtained by Caliskan, et al. ^[28]. TA: A

Exp. C. NCI: 4, Met: mild steel, Media:0.1 M HCl, Co: 0.1–0.5 gL⁻¹, t: 24, 168 h, T: 30, 60 °C, TA: A

Exp. C. NCI: 4, Met: mild steel, Media:0.1 M HCl, Co: 1–510⁻⁴ M, t: 168 h, T: 30 °C, TA: A

Exp. C. NCI: 16, Met: Armco iron, Media: HCl 1.0 M, Co: 10⁻³ M, et: 6 h (WL), 10 y 30 min (PP), T: 35 °C, TA: A

E_HOMO

E_LUMO

ΔE= E_{HOMO −}E_LUMO

It has been mentioned that the successful adsorption and proper efficiency of an inhibitor have been characterized by a high E_HOMO, a low E_LUMO_,and a small energy gap. The lower the ΔE is, the higher the stability of the metal-inhibitor interaction.