Quantum machine learning has emerged as a promising paradigm that could accelerate machine learning calculations. Inside this field, quantum reinforcement learning aims at designing and building quantum agents that may exchange information with their environment and adapt to it, with the aim of achieving some goal. Different quantum platforms have been considered for quantum machine learning and specifically for quantum reinforcement learning. Here, we review the field of quantum reinforcement learning and its implementation with quantum platforms. This quantum technology may enhance quantum computation and communication, as well as machine learning, via the fruitful marriage between these previously unrelated fields.
- quantum machine learning
- quantum reinforcement learning
- quantum photonics
- quantum technologies
- quantum communication
1. Introduction
The field of quantum machine learning promises to employ quantum systems for accelerating machine learning [1] calculations, as well as employing machine learning techniques to better control quantum systems. In the past few years, several books as well as reviews on this topic have appeared [2][3][4][5][6][7][8].
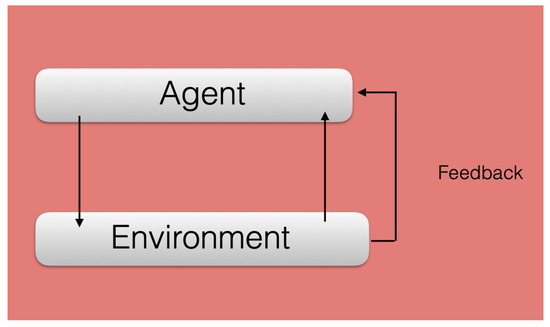
Inside artificial intelligence and machine learning, the area of reinforcement learning designs “intelligent” agents capable of interacting with their outer world, the “environment”, and adapt to it, via reward mechanisms [9], see Figure 1. These agents aim at achieving a final goal that maximizes their long-term rewards. This kind of machine learning protocol is, arguably, the most similar one to the way the human brain learns. The field of quantum machine learning is recently exploring the fruitful combination of reinforcement learning protocols with quantum systems, giving rise to quantum reinforcement learning [10][11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39].
Different quantum platforms are being considered for the implementation of quantum machine learning. Among them, trapped ions, superconducting circuits, and quantum photonics, seem promising due to the advanced development stage of the technology. In particular, the latter is appropriate because of the good integration with communication networks, information processing at the speed of light, as well as possible realization of quantum computations with integrated photonics [40]. Moreover, in the scenario with a reduced amount of measurements, quantum reinforcement learning with quantum photonics has been shown to perform better than standard quantum tomography [16]. Quantum reinforcement learning with quantum photonics has been proposed [17] and implemented [19] in diverse works. Even before these articles were produced, a pioneering experiment of quantum supervised and unsupervised learning with quantum photonics was carried out [41].
In this topic review, we give an overview of the field of quantum reinforcement learning, focusing mainly on quantum devices employed for reinforcement learning algorithms [10][11][12][13][14][15][16][17][18][19][20], in Section 2.
2. Quantum Reinforcement Learning
The fields of reinforcement learning and quantum technologies have started to merge recently in a novel area, named quantum reinforcement learning [10][11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31][32][33][34][35]. A subset inside this field is composed of articles studying quantum systems that carry out reinforcement learning algorithms, ideally with some speedup [10][11][12][13][14][15][16][17][18][19][20].
In Ref. [10], a pioneer proposal for reinforcement learning using quantum systems was put forward. This employed a Grover-like search algorithm, which could provide a quadratic speedup in the learning process as compared to classical computers [10].
Ref. [11] provided a quantum algorithm for reinforcement learning in which a quantum agent, possessing a quantum processor, can couple classically with a classical environment, obtaining classical information from it. The speedup in this case would come from the quantum processing of the classical information, which could be done faster than with classical computers. This is also based on Grover search, with a corresponding quadratic speedup.
In Ref. [12], a quantum algorithm considers a quantum agent coupled to a quantum oracular environment, attaining a proven speedup with this kind of configuration, which can be exponential in some situations. The quantum algorithm could be applied to diverse kinds of learning, namely reinforcement learning, but also supervised and unsupervised learning.
Refs. [10][11][12] have speedups with respect to classical algorithms. While the first two rely on a polynomial gain due to a Grover-like algorithm, the latter achieves its proven speedup via a quantum oracular environment.
The series of articles in Refs. [13][14][15][16][17][18] study quantum reinforcement learning protocols with basic quantum systems coupled to small quantum environments. These works focus mainly on proposals for implementations [13][14][15][17] as well as experimental realizations in quantum photonics [16] and superconducting circuits [18]. In the theoretical proposals, small few-qubit quantum systems are proposed both for quantum agents and quantum environments. In Ref. [13], the aim of the agent is to achieve a final state which cannot be distinguished from the environment state, even if the latter has to be modified, as it is a single-copy protocol. In order to achieve this goal, measurements are allowed, as well as classical feedback inside the coherence time. Ref. [14] extends the previous protocol to the case in which measurements are not considered, but instead further ancillary qubits coupled via entangling gates to agent and environment are employed, and later on disregarded. In Ref. [15], several identical copies of the environment state are considered, such that the agent, via trial and error, or, equivalently, a balance between exploration and exploitation, iteratively approaches the environment state. This proposal was carried out in a quantum photonics experiment [16] as well as with superconducting circuits [18]. In Ref. [17], a further extension of Ref. [15] to operator estimation, instead of state estimation, was proposed and analyzed.
Ref. [16] obtained a speedup as well with respect to standard quantum tomography, in the scenario with a reduced amount of resources, in the sense of reduced number of measurements.
Finally, Ref. [20] considered different paradigms of learning inside a reinforcement learning framework, which included projective simulation [42] and a possible implementation with quantum photonics devices. The latter, with high-repetition rates, high-bandwith and low crosstalks, as well as the possibility to propagate to long distances, makes this quantum platform an attractive one for this kind of protocol.
References
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson: London, UK, 2009. [Google Scholar]
- Wittek, P. Quantum Machine Learning; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Schuld, M.; Petruccione, F. Supervised Learning with Quantum Computers; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 2015, 56, 172. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 074001. [Google Scholar] [CrossRef] [PubMed]
- Dunjko, V.; Briegel, H.J. Machine learning & artificial intelligence in the quantum domain: A review of recent progress. Rep. Prog. Phys. 2018, 81, 074001. [Google Scholar] [PubMed]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. The quest for a Quantum Neural Network. Quantum Inf. Process. 2014, 13, 2567. [Google Scholar] [CrossRef]
- Lamata, L. Quantum machine learning and quantum biomimetics: A perspective. Mach. Learn. Sci. Technol. 2020, 1, 033002. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Dong, D.; Chen, C.; Li, H.; Tarn, T.-J. Quantum Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 38, 1207. [Google Scholar] [CrossRef]
- Paparo, G.D.; Dunjko, V.; Makmal, A.; Martin-Delgado, M.A.; Briegel, H.J. Quantum Speedup for Active Learning Agents. Phys. Rev. X 2014, 4, 031002. [Google Scholar] [CrossRef]
- Dunjko, V.; Taylor, J.M.; Briegel, H.J. Quantum-Enhanced Machine Learning. Phys. Rev. Lett. 2016, 117, 130501. [Google Scholar] [CrossRef]
- Lamata, L. Basic protocols in quantum reinforcement learning with superconducting circuits. Sci. Rep. 2017, 7, 1609. [Google Scholar] [CrossRef]
- Cárdenas-López, F.A.; Lamata, L.; Retamal, J.C.; Solano, E. Multiqubit and multilevel quantum reinforcement learning with quantum technologies. PLoS ONE 2018, 13, e0200455. [Google Scholar] [CrossRef]
- Albarrán-Arriagada, F.; Retamal, J.C.; Solano, E.; Lamata, L. Measurement-based adaptation protocol with quantum reinforcement learning. Phys. Rev. A 2018, 98, 042315. [Google Scholar] [CrossRef]
- Yu, S.; Albarrán-Arriagada, F.; Retamal, J.C.; Wang, Y.-T.; Liu, W.; Ke, Z.-J.; Meng, Y.; Li, Z.-P.; Tang, J.-S.; Solano, E.; et al. Reconstruction of a Photonic Qubit State with Reinforcement Learning. Adv. Quantum Technol. 2019, 2, 1800074. [Google Scholar] [CrossRef]
- Albarrán-Arriagada, F.; Retamal, J.C.; Solano, E.; Lamata, L. Reinforcement learning for semi-autonomous approximate quantum eigensolver. Mach. Learn. Sci. Technol. 2020, 1, 015002. [Google Scholar] [CrossRef]
- Olivares-Sánchez, J.; Casanova, J.; Solano, E.; Lamata, L. Measurement-Based Adaptation Protocol with Quantum Reinforcement Learning in a Rigetti Quantum Computer. Quantum Rep. 2020, 2, 293–304. [Google Scholar] [CrossRef]
- Melnikov, A.A.; Nautrup, H.P.; Krenn, M.; Dunjko, V.; Tiersch, M.; Zeilinger, A.; Briegel, H.J. Active learning machine learns to create new quantum experiments. Proc. Natl. Acad. Sci. USA 2018, 115, 1221. [Google Scholar] [CrossRef]
- Flamini, F.; Hamann, A.; Jerbi, S.; Trenkwalder, L.M.; Nautrup, H.P.; Briegel, H.J. Photonic architecture for reinforcement learning. New J. Phys. 2020, 22, 045002. [Google Scholar] [CrossRef]
- Fösel, T.; Tighineanu, P.; Weiss, T.; Marquardt, F. Reinforcement Learning with Neural Networks for Quantum Feedback. Phys. Rev. X 2018, 8, 031084. [Google Scholar] [CrossRef]
- Bukov, M. Reinforcement learning for autonomous preparation of Floquet-engineered states: Inverting the quantum Kapitza oscillator. Phys. Rev. B 2018, 98, 224305. [Google Scholar] [CrossRef]
- Bukov, M.; Day, A.G.R.; Sels, D.; Weinberg, P.; Polkovnikov, A.; Mehta, P. Reinforcement Learning in Different Phases of Quantum Control. Phys. Rev. X 2018, 8, 031086. [Google Scholar] [CrossRef]
- Melnikov, A.A.; Sekatski, P.; Sangouard, N. Setting up experimental Bell test with reinforcement learning. arXiv 2020, arXiv:2005.01697. [Google Scholar]
- Mackeprang, J.; Dasari, D.B.R.; Wrachtrup, J. A Reinforcement Learning approach for Quantum State Engineering. arXiv 2019, arXiv:1908.05981. [Google Scholar]
- Schäfer, F.; Kloc, M.; Bruder, C.; Lörch, N. A differentiable programming method for quantum control. arXiv 2002, arXiv:2002.08376. [Google Scholar] [CrossRef]
- Sgroi, P.; Palma, G.M.; Paternostro, M. Reinforcement learning approach to non-equilibrium quantum thermodynamics. arXiv 2020, arXiv:2004.07770. [Google Scholar]
- Wallnöfer, J.; Melnikov, A.A.; Dür, W.; Briegel, H.J. Machine learning for long-distance quantum communication. arXiv 2019, arXiv:1904.10797. [Google Scholar]
- Zhang, X.-M.; Wei, Z.; Asad, R.; Yang, X.-C.; Wang, X. When does reinforcement learning stand out in quantum control? A comparative study on state preparation. npj Quantum Inf. 2019, 5, 85. [Google Scholar] [CrossRef]
- Xu, H.; Li, J.; Liu, L.; Wang, Y.; Yuan, H.; Wang, X. Generalizable control for quantum parameter estimation through reinforcement learning. npj Quantum Inf. 2019, 5, 82. [Google Scholar] [CrossRef]
- Sweke, R.; Kesselring, M.S.; van Nieuwenburg, E.P.L.; Eisert, J. Reinforcement Learning Decoders for Fault-Tolerant Quantum Computation. arXiv 2018, arXiv:1810.07207. [Google Scholar] [CrossRef]
- Andreasson, P.; Johansson, J.; Liljestr, S.; Granath, M. Quantum error correction for the toric code using deep reinforcement learning. Quantum 2019, 3, 183. [Google Scholar] [CrossRef]
- Nautrup, H.P.; Delfosse, N.; Dunjko, V.; Briegel, H.J.; Friis, N. Optimizing Quantum Error Correction Codes with Reinforcement Learning. Quantum 2019, 3, 215. [Google Scholar] [CrossRef]
- Fitzek, D.; Eliasson, M.; Kockum, A.F.; Granath, M. Deep Q-learning decoder for depolarizing noise on the toric code. Phys. Rev. Res. 2020, 2, 023230. [Google Scholar] [CrossRef]
- Fösel, T.; Krastanov, S.; Marquardt, F.; Jiang, L. Efficient cavity control with SNAP gates. arXiv 2020, arXiv:2004.14256. [Google Scholar]
- McKiernan, K.A.; Davis, E.; Alam, M.S.; Rigetti, C. Automated quantum programming via reinforcement learning for combinatorial optimization. arXiv 2019, arXiv:1908.08054. [Google Scholar]
- Garcia-Saez, A.; Riu, J. Quantum Observables for continuous control of the Quantum Approximate Optimization Algorithm via Reinforcement Learning. arXiv 2019, arXiv:1911.09682. [Google Scholar]
- Khairy, K.; Shaydulin, R.; Cincio, L.; Alexeev, Y.; Balaprakash, P. Learning to Optimize Variational Quantum Circuits to Solve Combinatorial Problems. arXiv 2019, arXiv:1911.11071. [Google Scholar] [CrossRef]
- Yao, J.; Bukov, M.; Lin, L. Policy Gradient based Quantum Approximate Optimization Algorithm. arXiv 2020, arXiv:2002.01068. [Google Scholar]
- Flamini, F.; Spagnolo, N.; Sciarrino, F. Photonic quantum information processing: A review. Rep. Prog. Phys. 2019, 82, 016001. [Google Scholar] [CrossRef]
- Cai, X.-D.; Wu, D.; Su, Z.-E.; Chen, M.-C.; Wang, X.-L.; Li, L.; Liu, N.-L.; Lu, C.-Y.; Pan, J.-W. Entanglement-Based Machine Learning on a Quantum Computer. Phys. Rev. Lett. 2015, 114, 110504. [Google Scholar] [CrossRef]
- Briegel, H.J.; De las Cuevas, G. Projective simulation for artificial intelligence. Sci. Rep. 2012, 2, 1. [Google Scholar] [CrossRef]
