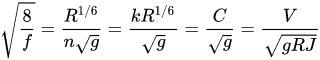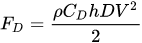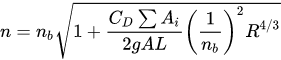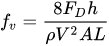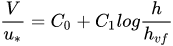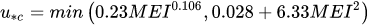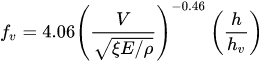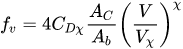Flow Resistance Due to Vegetation: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Antonino D’Ippolito and Version 3 by Dean Liu.

Vegetation on the riverbed, banks and flooding areas of watercourses significantly affects energy losses. Energy dissipation takes on different values depending on whether the vegetation is emergent or submerged, rigid or flexible. Many models have been proposed in the scientific literature for its evaluation.

  • river hydraulics
  • vegetation
  • flow resistance
  • numerical methods
  • turbulence
  • remote sensing

Contributors: Antonino D’Ippolito, Francesco Calomino, Giancarlo Alfonsi, Agostino Lauria

 

1. Introduction

Vegetation is an important issue on the viewpoint of catchment hydrology

[1][2][3]

, since rain drops interception, evapotranspiration, infiltration are elements to consider in surface and sub-surface water balance. Moreover, riparian vegetation plays a key role both on the ecologic and habitat viewpoints, as well as a source of biodiversity. Indeed, vegetation prevents fertilizers and pollutants from getting to the watercourses

[4]

and, because of the effect on landscape, has a significant recreational function.

On a more strictly technical viewpoint, riparian vegetation interacts with water flow, with effects both on the bank stability and on the river hydraulics. Vegetation acts on bank stability since it mechanically strengthens the soil because of the presence of roots

[5][6][7][8]

; moreover, it reduces the soil water content because of evapotranspiration with the consequence of reducing interstitial pressures

[9]

.

As to river hydraulics, vegetation clutters up part of the river cross-section

[7][10][11]

, increases the roughness and reduces the velocity; all this results in increased water levels and reduced water conveyance. Moreover, while the smaller average velocity on one hand reduces the erosion of riverbed and banks, on the other one increases the sediment deposition, what makes the water cross-sections smaller and raises flooding risk. On the scale of the hydrographic network, the general velocity reduction influences the travel time of water particles, making easier the peak flow control

[12][13]

.

Therefore, one cannot know in advance the general effect of vegetation, but every case should be considered singularly, using proper procedures. Indeed, this effect depends on both the hydraulic and mechanical properties of the water cross-section, as to of the present vegetation, that may be different according to species, phenological stage, age and, possibly, maintenance.

Usually, in the literature the vegetation is considered as rigid or flexible, and according to the water level, as emergent or submerged. Flexible vegetation refers to grass, reeds and shrubs, or, when speaking about trees, to the branch and leaf system. Combinations of the above categories, really found in natural streams and channels, are still difficult to treat.

In the following we will present the methods found in the literature, allowing estimation of flow resistance coefficients to input into models for flood simulation, based on different types of vegetation in the river banks and floodplains.

2. Flow resistance equations

According to Chow

[14]

, the resistance to flow in artificial channels and watercourses is influenced by several factors, i.e. size and shape of the grains of the material forming the wetted perimeter, vegetation, silting and scouring, , etc.

As it is well known the resistance to flow can be expressed by the Darcy-Weisbach

f

friction factor, the Chézy’s

C

or the Gauckler-Strickler

k

velocity coefficients and the Manning

n

roughness coefficient; the relation among these coefficients is the following

(1)

where

V

is the mean flow velocity,

R

the hydraulic radius,

J

the energy line slope and

g

the gravity acceleration.

The contribution of vegetation to the roughness coefficient can be evaluated by means of descriptive approaches, photographic comparison approaches or by analytical methods.

3. Descriptive and photographic comparison approaches

In these methods, one roughness coefficient is chosen on the basis of the class to which the river reach belongs. Among the descriptive methods, the best known is the Chow’s one[14]. The author gives, for every class of channels, the minimum, average and maximum values of Manning n coefficient, warning that when the channel is artificial, the average values should be used in case of good maintenance only. The photographic comparison approach consists in evaluating the Manning coefficient of a given river reach on the basis of similarity with the pictures of other similar cases, for which the coefficient was estimated in ordinary or flood conditions.

4. Analytical methods

4.1 Rigid vegetation

When the vegetation is made up by trees, in an analogy of the resistance to flow due to immersed bodies, the roughness coefficient is expressed as a function of the drag force exerted by the flow on the body, depending then on the number of trees, their arrangement, the diameters of their trunks and, where appropriate, the branch system. Usually, in the laboratory tests, the rigid vegetation is simulated by cylinders.

4.1.1. Emergent rigid vegetation

In case of one isolated vertical cylinder whose axis is orthogonal to the flow direction the resistance to flow is expressed by the drag force

FD

, computed as

(2)

where

ρ

 is the water density,

h

is the depth of the immersed part of the cylinder,

V

is the approach velocity and

CD

is a drag coefficient.

CD

is a function of stem Reynolds number computed by means of the approach velocity

V

and the cylinder diameter

D

, , being

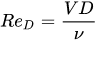
ν

the water kinematic viscosity.

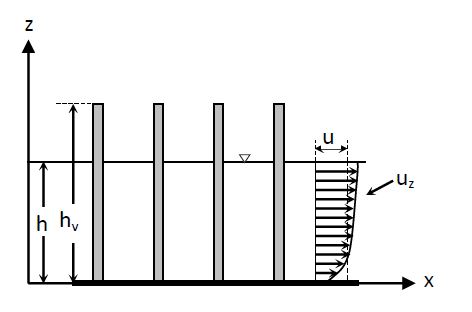
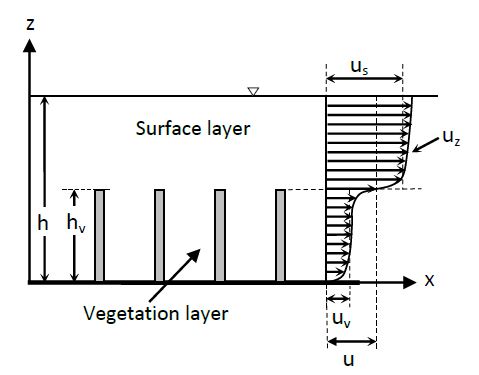
When the cylinder is a part of a group of elements (see Fig. 1), one cannot ignore that the longitudinal and transversal interference make considerably more difficult the study of the resistance to flow

[15][16][17]

. In Fig. 1

x

is the streamwise coordinate,

z

is the vertical coordinate above the river bed,

uz

is the local time-averaged velocity,

u

is the mean velocity along the vertical,

h

is the water depth and

hv

the vegetation height.

Figure 1. Side view of emergent vegetation and velocity profile.

Figure 1. Side view of emergent vegetation and velocity profile.

To find the values of CD in case of sparse emergent arrays, both experimental tests and numerical simulations have been carried out, with the vegetation arrangements defined before as linear, or staggered, or random. Among the first studies, we will cite only Petryk[18], Li and Shen[15] and Petryk and Bosmajian[19].

Petryk and Bosmajian

[19]

, to determine the Manning coefficient in a vegetated channel, implement the momentum equation for a reach, imposing that be equal to zero the vector sum of the weight of the control volume, projected on the bed direction, plus the contour resistance, plus that opposed by the tree trunk; they conclude with defining the overall Manning coefficient

n

as a function of the value relative to the soil,

nb

, and the one relative to vegetation drag coefficient

CD

, by writing

(3)

where

L

is the reach length,

A

the area of the water cross-section, Σ

Ai

the area opposed by the vegetation to the flow. The authors consider equal to 1 the drag coefficient

CD

. For the estimation of C

D

several expression have been proposed

[20][21][22][23][24][25]

.

4.1.2. Submerged rigid vegetation

In the case of submerged vegetation, very often the profile is schematized as only two interacting zones (two-layer approach): the vegetation layer, containing the cylindrical elements representing the vegetation, and the surface layer, above them, up to the flow surface (Fig. 2). In Fig. 2

us

is the mean velocity along the vertical in the surface layer, and

uv

is the mean velocity along the vertical in the vegetated layer.

Figure 2. Side view of submerged vegetation and velocity profile

Figure 2. Side view of submerged vegetation and velocity profile

Rigid submerged vegetation has been the subject of a large number of investigations

[7][26][27][28][29][30][31][32]

and comparisons

[33][34][35][36][37][38]

. Some researchers provided the average velocity values in the two layers while others derived the velocity distribution and the average values

[7][28][29][31]

. In the vegetation layer the streamwise velocity is usually considered constant with the flow depth

[27][31]

, while in the surface layer various expressions were adopted for the velocity distribution

[36]

: the logarithmic theory

[26][28][31]

, the Kolmogorov theory of turbulence

[30]

, the genetic programming

[27]

, the representative roughness height

[32][39]

.

Starting from the velocity distribution it is possible to evaluate the Manning coefficient

[27][30][31][39]

, and some authors

[11][40]

have proposed expressions for both submerged and emergent rigid vegetation.

4.2 Flexible vegetation

4.2.1. Potentially changing vegetation condition

Sometimes during a flood event, as the discharge increases, the vegetation can lay over or be removed

[41][42][43][44]

, which leads to a reduction in roughness and to an increase in the flow capacity through the section; therefore the peak flow, which could occur later, takes lower water-surface elevations than it would have had in the case of upright vegetation. To determine under what conditions the vegetation flattens, Phillips et al.

[41]

referred to the stream power, defined as

SP=gRJV

, and to the resistance of the vegetation characterized by an index defined as the susceptibility index of the vegetation. This index is given by the product of the vegetation flexibility factor, the vegetation blocking coefficient, the vegetation distribution coefficient and, finally, the flow depth coefficient. For each type of vegetation it is possible to determine the minimum value of the stream power beyond which the vegetation is layover.  

For rigid vegetation, the action of the flow varies with the squared velocity. In case of flexible vegetation, this is not true, since the vegetation reconfigures by reducing the area projected on a plane orthogonal to the flow direction and aligning the leaves with it. The relationship between flow velocity and drag force was expressed as 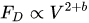, where the Vogel exponent

b[17]

, is a measure of the plant reconfiguration. When is

b =

1, the drag force varies linearly with the velocity. A linear increase of drag force with the flow velocity was observed for flexible plants by direct measurement in prototype scale by Armanini et al.

[45]

.

The friction factor due to the vegetation, fv, in a reach of length L is

 (4)

We will first analyze the studies in the case of submerged flexible vegetation and then those related to the non-submerged vegetation.

4.2.2. Submerged flexible vegetation

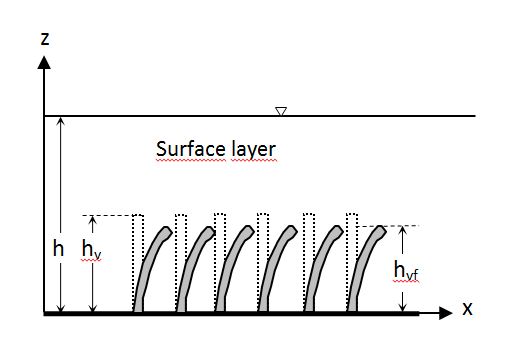
The first studies on submerged flexible vegetation (Fig. 3) are related to the design of irrigation canals

[46]

. In Fig. 3

hvf

is the bent vegetation height. Since the resistance depends on the curvature of the vegetation, the link between the Manning coefficient,

n

, and the product of velocity,

V

, and hydraulic radius,

R

, was identified on an experimental basis. This relationship depends on the type of vegetation and is practically independent on the slope of the canal and its shape. Five experimental curves have been obtained relating the Manning coefficients, also called delay coefficients, with the product

VR

classified as very high, high, moderate, low or very low and identified with the letters A, B, C, D and E.

Figure 3. Side view of submerged flexible vegetation.

Figure 3. Side view of submerged flexible vegetation.

According to Kouwen et al.

[47]

the friction factor in the case of submerged flexible vegetation can be represented through a semi-logarithmic function of the relative roughness, defined as the ratio of the deflected plant height,

hvf

, to the flow depth

    (5)

where the coefficients C0 and C1 depend on u*/u*c with

    (6)

where

M

is the stem count per unit area,

E

is the modulus of elasticity and

I

the second moment of the cross-sectional area of the stems. The product

MEI

is defined as flexural rigidity. The deflected height depends on the drag exerted by the flow and the flexural rigidity of the vegetation.

 

4.2.3. Non submerged flexible vegetation

Studies on non-submerged flexible vegetation have been carried out, among others, by Kouwen and Fathi Moghadam

               Studies on non-submerged flexible vegetation have been carried out, among others, by Kouwen and Fathi Moghadam

[48]

, and Västilä et al.

[49]

.

Kouwen and Fathi Moghadam

[48]

, performed laboratory experiments on four different types of conifers both in water and in air; the authors, on the basis of dimensional analysis and a series of symplifyng hypotheses proposed to calculate the friction factor as the following equation

        

(7)

where

ξ

takes into account the deformation of the plant, and

E

is the modulus of elasticity. The term

ξE

 is called vegetation index, it is unique for each species and is obtained from the resonant frequency, mass and length of a tree

[48][50]

.

               Recently, Västilä et al.[49] proposed to calculate the friction factor, fv, as

(8)

where

Ac

 represents a characteristic area of plants,

Ab

is the bed area related to a plant,

CDχ

 is a species-specific drag coefficient,

χ

 depends on the area , and

Vχ

is the lowest velocity used in determining

χ

. As to the area

Ac

, Västilä et al.

[49]

compared three areas: the first one,

AL

, is obtained by means of the leaf area index (LAI), (defined as the ratio between the one-sided leaf area and the ground area), the second one as the area projected onto a plan orthogonal to the flow direction when the plant is under the flow action (

Ap

), and the third one as the area projected onto a plan orthogonal to the flow direction when the plant is on free air (

A0

).

5. Numerical Methods

For a detailed analysis of the flow fields and turbulence characteristics one can refer to measurements with  particle image velocimetry system (PIV) or acoustic Doppler velocimeter (ADV) probe or, furthermore, on numerical simulations, more or less detailed depending on the flow cases at hand

[22][51][52][53][54]

[22,51-54]. An excellent review about the numerical models utilized for the analysis of the interaction between flow and vegetation is due to Stoesser et al.

[55]

.

RANS models are operated on coarse grids and the drag due to vegetation is accounted for through additional source terms in the governing equations

[56][57][58][59][60]

[56-60]. The coherent structures that form downstream to the cylinders or over the vegetated layer in the case of submerged vegetation can be obtained by means of LES approach

[61][62][63]

. In the latter simulations, one can explicitly represent the plants by inserting in the mesh some blocked cells representing the vegetation. Stoesser et al.

[61]

[61] executed a LES with reference to a companion experiment of Liu et al.

[64]

related to rigid emergent vegetation, obtaining interesting results. It should be noted that numerical simulations have been used not only for comparisons with companion experiments, but also in real situations. As an example

[55][65]

, a RANS simulation was carried out to mirror a flood event of the Rhine river with a return period of 100 years.

6. Hydraulic roughness assessment

Riparian vegetation, in particular that located on flood areas, has very heterogeneous characteristics both from a spatial and temporal point of view. These characteristics must be adequately included in the hydraulic-hydrological models. Conventional ground-based monitoring is often unfeasible as these techniques are time-demanding and expensive

[66]

, especially for large areas and when they are inaccessible. New opportunities are offered by remote sensing, which has developed considerably in recent decades and has been increasingly used in the environmental field. Some reviews have addressed the use of remote sensing in fluvial studies

[67][68][69]

and, in particular, for mapping riparian vegetation and estimating biomechanical parameters

[70]

.

Remote sensing is based on satellite images (digital or radar) or aerial platforms (LiDAR (Light Detection and Ranging) and orto-photography). Digital satellite images, in the last decade, have reached a definition similar to those of orthophotos (the pixel sizes in the sensors Quickbird and Ikonos are equal, respectively, to 0.6 m and 1 m) making it possible their application to riparian areas that, very often, are of limited size. Image classification is the process of assigning individual pixel or groups of pixels to thematic classes

 The vegetation hydrodynamic maps are also able to well describe the equivalent Manning’s roughness coefficient[71].

One of the biggest limitations of optical sensors is the inability to penetrate the cloud system. Radar systems are microwave-based and do not depend on the cloud system and are particularly useful during flooding events, that usually occur in the presence of a cloud cover, allowing monitoring of the timing and spatial extent of flooding. Backscatter increases with biomass and this makes it difficult to apply radar sensors in floodplain areas which are usually characterized by very dense vegetation.

Satellite images provide information on the spatial variability of vegetation but do not provide information about its vertical structure. LiDAR technology provides information on the three-dimensional structure of vegetation. Laser scanning (LS) is employed in terrestrial (TLS), airborne (ALS) and mobile (MLS) platforms. The airborne laser scanner (ALS) provide accurate information of forest canopy and ground elevations producing a digital terrain model and a digital surface model. The difference between the digital surface model and the digital terrain model gives the tree heights.

7. Future directions

Currently research on the interaction between vegetation and flow is focusing on a more correct assessment of the action exerted by the shear stress

[72][73]

, on velocity distribution

[74][75]

, on sediment transport

[76][77][78][79][80][81][82]

, on finite-sized vegetation patches

[83][84][85][86][87][88][89][90]

, on the interaction between jets and vegetation

[91][92]

, on processes of transport and dispersion

[93][94][95]

, on evolution of patches of vegetation

[96]

and on one-line emergent vegetation

[97]

. New opportunities seem to be offered by the use of remote sensing in fluvial studies

[67][68][69]

and, in particular, for mapping riparian vegetation and estimating biomechanical parameters

[70]

.

References

  1. Penman, H.L.. Vegetation and Hydrology; Commonwealth Agricultural Bureau: Harpenden , 1963; pp. 124 .
  2. Peel, M.C. Hydrology: catchment vegetation and runoff. Prog. Phys. Geog. 2009, 33(6), 837-844.
  3. D'Ippolito, A.; Ferrari, E.; Iovino, F.; Nicolaci, A.; Veltri, A. Reforestation and land use change in a drainage basin of Southern Italy. iForest 2013, 6: 175-182.
  4. Rowiński, P.M.; Västilä, K.; Aberle, J.; Järvelä, J.; Kalinowska, M. How vegetation can aid in coping with river management challenges: A brief review. Ecohydrol. Hydrobiol. 2018, 18(4), 345-354.
  5. Wynn, T.S.; Mostaghimi, S. The effects of vegetation and soil type on streambank erosion, southwestern Virginia, USA. J. Am. Water Resour. As. 2006, 42(1), 69–82.
  6. Afzalimehr, H.; Dey, S. Influence of bank vegetation and gravel bed on velocity and Reynolds stress distributions. Int. J. Sediment Res., 2009, 24(2), 236–246.
  7. Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50(3), 262–279.
  8. Krzeminska, D.; Kerkhof, T.; Skaalsveen, K.; Stolte, J. Effect of riparian vegetation on stream bank stability in small agricultural catchments. Catena 2019, 172, 87–96.
  9. Julien, P.Y. River Mechanics. Cambridge University Press, Cambridge, UK, 2002.
  10. Green, J.C. Comparison of blockage factors in modelling the resistance of channels containing submerged macrophytes. River Res. Applic. 2005, 21, 671–686.
  11. Luhar, M.; Nepf, H.M. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 2013, 51, 305-316
  12. Anderson, B.G.; Rutherfurd, I.D.; Western, A.W. An analysis of the influence of riparian vegetation on the propagation of flood waves. Environ. Modell. Softw. 2006, 21(9), 1290-1296.
  13. Rutherfurd, I.D.; Anderson, B.; Ladson, A. Managing the effects of riparian vegetation on flooding. In: Principles for riparian lands management. Lovett S., Price P. Ed., Land and Water Australia, 2007, 190 p.
  14. Chow, V.T. Open channel hydraulics. McGraw-Hill Book Co., New York. 1959, 680 p.
  15. Li, R.M.; Shen, H.W. Effect of tall vegetations on flow and sediment. Journal of Hydraulics Division 1973, 99(5), 793-814.
  16. Nepf, H.M. Drag, turbulence and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35(2), 479-489.
  17. Aberle J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51(1), 33-45.
  18. Petryk, S. Drag on cylinders in open channel flow. Thesis presented to Colorado State University, Fort Collins, Colorado, 1969.
  19. Petryk, S.; Bosmajian, G. Analysis of flow through vegetation. Journal of Hydraulics Division 1975, 101(7), 871-884.
  20. Ishikawa, Y.; Mizuhara, K.; Ashida, S. Effect of density of trees on drag exerted on trees in river channels. J. For. Res. 2000, 5(4), 271-279.
  21. Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47(6), 691-699.
  22. D’Ippolito, A.; Lauria, A.; Alfonsi, G.; Calomino, F. Investigation of flow resistance exerted by rigid emergent vegetation in open channel. Acta Geophys. 2019, 67(3), 971-986.
  23. Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134(1), 34-41.
  24. Cheng, N.S.; Nguyen, H.T. Hydraulic radius for evaluating resistance induced by simulated emergent vegetation in open-channel flow. J. Hydraul. Eng. 2011, 137(9), 995-1004.
  25. Wang H., Tang H.W., Yuan S.Y., Lv S.Q., Zhao X.Y. An experimental study of the incipient bed shear stress partition in mobile bed channels filled with emergent rigid vegetation. Sci. China Technol. Sci. 2014, 57(6), 1165-1174.
  26. Stone, M.C.; Shen, H.T. Hydraulic resistance of flow in channel with cylindrical roughness. J. Hydraul. Eng. 2002, 128(5), 500-506.
  27. Baptist M.J.; Babovic V.; Rodríguez Uthurburu J.; Keijzer M.; Uittenbogaard R.E.; Mynett A.; Verwey A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45(4), 435-450.
  28. Klopstra, D.; Barneveld, H.J.; van Noortwijk, J.; van Velzen, E. Analytical model for hydraulic roughness of submerged vegetation. In Proceedings of the 27th IAHR Congress, San Francisco, CA, USA, 10-15 August 1997; 775–780.
  29. Defina, A.; Bixio, A.C. Mean flow and turbulence in vegetated open channel flow. Water Resour. Res. 2005, 41, W07006.
  30. Huthoff, F.; Augustijn, D.; Hulscher, S. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res.,2007, 43(6): W06413
  31. Yang, W.; Choi, S. A two-layer approach for depth-limited open-channel flows with submerged vegetation. J. Hydraul. Res. 2010, 48(4), 466-475.
  32. Li, S.; Shi, H.; Xiong, Z.; Huai, W.; Cheng, N. New formulation for the effective relative roughness height of open channel flows with submerged vegetation. Adv. Water Resour. 2015, 86, 46-57.
  33. Augustijn D.C.M., Galema A.A., Huthoff F. Evaluation of flow formulas for submerged vegetation. EUROMECH Colloquium 523 Ecohydraulics: linkages between hydraulics, morphodynamics and ecological processes in rivers Clermont-Ferrand, France, 15-17 June.
  34. Vargas-Luna, A.; Crosato, A.; Uijttewaal W.S.J. Effects of vegetation on flow and sediment transport: comparative analyses and validation of predicting models. Earth Surf. Process. Landform 2015, 40, 157-176.
  35. Morri, M.; Soualmia, A.; Belleudy, P. Mean velocity modeling of open chnnel flow with submerged rigid vegetation. International Journal of Mechanical and Mechatronics Engineering, 2015, 9, 302-307.
  36. Pasquino, V.; Gualtieri, P. Flow resistance of submerged rigid vegetation: focus and validation on two layer approach. In Proceedings of the 37th IAHR World Congress, Kuala Lampur, Malaysia, 13-18 August 2017; 2502-2510.
  37. Romdhane, H.; Soualmia, A.; Cassan, L.; Dartus, D. Flow over flexible vegetated bed: evaluation of analytical models. J. Appl. Fluid Mech., 2019, 12(2), 351-359.
  38. Tang, X. Evaluating two-layer models for velocity profiles in open-channels with submerged vegetation. Journal of geoscience and environment Protection, 2019, 7, 68-80.
  39. Cheng, N.S. Representative roughness height of submerged vegetation, Water Resour. Res. 2011, 47, W08517.
  40. Katul, G.; Wiberg, P.; Albertson, J.; Hornberger G. A mixing layer theory for flow resistance in shallow streams. Water Resour. Res. 2002, 38(11), 1250.
  41. Phillips, J.V.; McDoniel, D.; Capesius, J.P.; Asquith, W. 1998b - Method to estimate effects of flow-induced vegeta¬tion changes on channel conveyances of streams in Central Arizona; U.S. Geological Survey: Tucson, Arizona, USA, 1998; Water-Resources Investi¬gations Report 98-4040, 43 p.
  42. Phillips, J.V.; Tadayon, S. Selection of Manning’s roughness coefficient for natural and constructed vegetated and non-vegetated channels, and vegetation maintenance plan guidelines for vegetated channels in Central Arizona; U.S. Geological Survey: Reston, Virginia, USA, 2007; Scientific Investigations Report 2006-5108, 41 p.
  43. Carollo F.G.; Ferro V.; Termini D. Flow resistance law in channel with flexible submerged vegetation. J. Hydraul. Eng. 2005, 131(7), 554-564.
  44. Francalanci, S.; Paris, E.; Solari, L. On the vulnerability of woody riparian vegetation during flood events. Environ. Fluid Mech. 2020, 20, 635-661.
  45. Armanini A.; Righetti M.; Grisenti P. Direct measurement of vegetation resistance in prototype scale. J. Hydraul. Res. 2005, 42(5), 481-487.
  46. Palmer, V.J. A method for designing vegetated waterways. J. Agric. Eng. 1945, 26 (12), 516-520.
  47. Kouwen, N.; Li, R.M.; Simons, D.B. Flow resistance in vegetated waterways. Trans. ASAE 1981, 24(3), 684-698.
  48. Kouwen, N.; Fathi-Moghadam, M. Friction factors for coniferous trees along rivers. J. Hydraul. Eng. 2000, 126(10), 732-740.
  49. Västilä, K.; Järvelä, J.; Aberle, J. Characteristic reference areas for estimating flow resistance of natural foliated vegetation. J. Hydrol. 2013, 492, 49-60.
  50. Fathi-Moghadam, M.; Kowen, N. Non-rigid, non-submerged, vegetation roughness in flood plains. J. Hydraul. Eng. 1997, 123(1), 51-57.
  51. Alfonsi, G. Reynolds Averaged Navier-Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62 (7), Art. 040802.
  52. Lauria, A.; Calomino, F.; Alfonsi, G.; D’Ippolito, A. Discharge coefficients for sluice gates set in weirs at different upstream wall inclinations. Water 2020, 12, 245.
  53. Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and numerical study of free-surface flows in a corrugated pipe. Water 2018, 10 (5), 638
  54. Alfonsi, G.; Ferraro D.; Lauria A.; Gaudio R. Large-eddy simulation of turbulent natural-bed flow. Phis. Fluids 2019, 31, 085105.
  55. Stoesser, T.; Neary, V.; Wilson, C.A.M.E. Modelling vegetated channel flows: challenges and opportunities. Presented at: WSEAS (The World Scientific and Engineering Academy and Society) Conference on Fluid Mechanics, Corfu, Greece, 2005.
  56. López, F.; García, M. Open channel flow through simulated vegetation: turbulence modeling and sediment transport. U.S. Army Corps of Engineers, Waterways Experiment Station. U.S. Army Corps of Engineers: Washington, D.C., USA, 1997; Wetland Research Technical Report WRP-CP-10, 106 p.
  57. Fischer-Antze, T.; Stoesser, T.; Bates, P.; Olsen, N.R.B. 3D numerical modelling of open-channel flow with submerged vegetation. J. Hydraul. Res. 2001, 39(3), 303-310.
  58. Shimizu, Y.; Tsujimoto, T. Numerical analysis of turbulent open channel flow over a vegetation layer using a k-ε turbulence model. Journal of Hydroscience and Hydraulic Engineering 1994, 11(2), 57-67.
  59. Choi, S.U.; Kang, H. Reynolds stress modeling of vegetated open-channel flows. J. Hydraul. Res.2004, 42(1), 3-11.
  60. López, F.; García, M. Mean flow and turbulent structure of open channel flow through non-emergent vegetation. J. Hydraul. Eng. 2001, 127(5), 392-402.
  61. Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent flow through idealized emergent vegetation. J. Hydraul. Eng. 2010, 136(12), 1003-1017.
  62. Cui, J.; Neary, V.S. Large eddy simulation (LES) of fully developed flow through vegetation. In: Proceedings of the Fifth International Conference on Hydroinformatics, Cardiff, UK 2002.
  63. Kim, S.J.; Stoesser, T. Closure modeling and direct simulation of vegetation drag in flow through emergent vegetation. Water Resour. Res. 2011, 47, W10511.
  64. Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. 2008, 113, F04015.
  65. Stoesser, T.; Wilson, C.A.M.E.; Bates, P.D.; Dittrich, A. Application of a 3D numerical model to a river with vegetated floodplains. J. Hydroinform. 2003, 5(2), 99-112.
  66. Dudley, S.J.; Bonham, C.D.; Abt, S.R.; Fischenich, J.G. Comparison of methods for measuring woody riparian vegetation density. J. Arid Environ. 1998, 38, 77-86.
  67. Hohenthal, J.; Alho, P.; Hyyppa, J.; Hyyppa, H. 2011 - Laser scanning applications in fluvial studies. Prog. Phys. Geog. 2011, 35(6), 782-809.
  68. Tomsett, C.; Leyland, J. Remote sensing of river corridors: A review of current trends and future directions. River Res. Applic. 2019, 35, 779-803.
  69. Huylenbroeck, L.; Laslier, M.; Dufour, S.; Georges, B.; Lejeune, P.; Michez, A. Using remote sensing to characterize riparian vegetation: a review of available tools and perspectives for managers. J. Environ. Manage. 2019, 267.
  70. Forzieri, G.; Castelli, F.; Preti, F. Advances in remote sensing of hydraulic roughness. Int. J. Remote Sens. 2012, 33(2), 630-654.
  71. Forzieri, G.; Degetto, M.; Righetti, M.; Castelli, F.; Preti, F. Satellite multispectral data for improved floodplain roughness modelling. J. Hydrol. 2011, 407, 41-57.
  72. Yang, J.Q.; Kerger, F.; Nepf, H.M. Estimation of the bed shear stress in vegetated and bare channels with smooth bed. Water Resour. Res. 2015, 51, 3647-3663.
  73. Liu, D.; Valyrakis, M.; Williams, R. Flow hydrodynamics across open channel flows with riparian zones: implications for riverbank stability. Water 2017, 9, 720.
  74. Ben Meftah, M.; Mossa M. Prediction of channel flow characteristics through square arrays of emergent cylinders. Phys. Fluids 2013, 25, 045102.
  75. Ben Meftah, M.; Mossa, M. A modified log-law of flow velocity distribution in partly obstructed open channels. Environ. Fluid Mech. 2016, 16, 453-479.
  76. Yang, J.Q.; Chung, H.; Nepf, H.M. The onset of sediment transport in vegetated channels predicted by turbulent kinetic energy. Geophys. Res. Lett. 2016, 43, 11,261–11,268.
  77. Tang, C.; Lei, J.; Nepf, H. M. Impact of vegetation-generated turbulence on the critical, near-bed, wave-velocity for sediment resuspension. Water Resour. Res. 2019, 55(7), 5904-5917.
  78. Västilä, K.; Järvelä, J. Characterizing natural riparian vegetation for modeling of flow and suspended sediment transport. J. Soils Sediments 2018, 18(10), 3114-3130.
  79. Box, W.; Västilä, K.; Järvelä, J. The interplay between flow field, suspended sediment concentration, and net deposition in a channel with flexible bank vegetation. Water 2019, 11(11), 2250.
  80. Yang, J.Q.; Nepf, H.M. Impact of vegetation on bed load transport rate and bedform characteristics. Water Resour. Res. 2019, 55(7), 6109-6124.
  81. Armanini, A.; Cavedon, V. Bed-load through emergent vegetation. Adv. Water Resour. 2019, 129, 250–259.
  82. Li J.F.; Tfwala S.S.; Chen S.C. Effects of vegetation density and arrangement on sediment budget in a sediment-laden flow. Water 2018, 10, 1412.
  83. Sukhodolova, T.; Sukhodolov, A. Vegetated mixing layer around a finite-size patch of submerged plants: 1. Theory and field experiments, Water Resour. Res. 2012, 48, W10533
  84. Sukhodolov, A., and T. Sukhodolova, T. Vegetated mixing layer around a finite-size patch of submerged plants: 2. Turbulence and coherent structures, Water Resour. Res. 2012, 48, W12506
  85. Yilmazer, D.; Ozan, A.Y.; Cihan, K. Flow characteristics in the wake region of a finite-length vegetation patch in a partly vegetated channel. Water 2018, 10(4), 459.
  86. Li, W.; Wang, D.; Jiao, J.; Yang, K. Effects of vegetation patch density on flow velocity characteristics in an open channel. J. Hydrodyn. 2018, available online at https://doi.org/10.1007/s42241-018-0086-6
  87. Cheng, N.S.; Hui, C.L.; Wang, X.; Tan, S.K. Laboratory study of porosity effect on drag induced by circular vegetative patch. J. Eng. Mech. 2019, 145(7).
  88. Kitsikoudis, V.; Yagci, O.; Kirca, V.S.O. Experimental analysis of flow and turbulence in the wake of neighboring emergent vegetation patches with different densities. Environ. Fluid Mech. 2020, 1417–1439.
  89. Yan, C.; Shan, Y.; Sun, W.; Liu C.; Liu X. Modeling the longitudinal profiles of streamwise velocity in an open channel with a model patch of vegetation. Environ. Fluid Mech. 2020, 1441–1462.
  90. Liu, C.; Shan, Y. Analytical model for predicting the longitudinal profiles of velocities in a channel with a model vegetation patch. J. Hydrol. 2019, 576, 561–574.
  91. Mossa, M.; De Serio, F. Rethinking the process of detrainment: jets in obstructed natural flows. Sci. Rep. 6, 39103; 2016, doi: 10.1038/srep39103.
  92. Mossa, M.; Ben Meftah M.; De Serio F.; Nepf H.M. How vegetation in flows modifies the turbulent mixing and spreading of jets. Sci. Rep. 7, 6587; 2017, doi: 10.1038/s41598-017-05881-1.
  93. De Serio, F.; Ben Meftah M.; Mossa M.; Termini D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2017, 120, 98-113.
  94. Termini, D. Turbulent mixing and dispersion mechanisms over flexible and dense vegetation. Acta Geophys. 2019, 67(3), 961-970.
  95. Zhang, J.; Huai, WX.; Shi, HR.; Wang, W.J. Estimation of the longitudinal dispersion coefficient using a two-zone model in a channel partially covered with artificial emergent vegetation. Environ. Fluid Mech. 2020.
  96. Yamasaki, T.N.; de Lima, P.H.; Silva, D.F.; Cristiane, G.D.A.; Janzen, J.G.; Johannes, G.; Nepf, H.M. From patch to channel scale: The evolution of emergent vegetation in a channel. Adv. Water Res. 2019, 129, 131–145.
  97. Mulahasan, S.; Stoesser, T. Flow resistance of in-line vegetation in open channel flow. Int. J. River Basin Manag. 2017, 15(3), 329-334.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback