Molecular dynamics (MD) is a simulation technique that aims at deriving statements about the structural, dynamical, and thermodynamical properties of a molecular system. MD simulations hans have become increasingly useful in the modern drug development process. For example, iIn the lead discovery and lead optimization phases, MD facilitates the evaluation of the binding energetics and kinetics of the ligand-receptor interactions, therefore guiding the choice of the best candidate molecules for further development. in the future, the role of MD simulations in facilitating the drug development process is likely to grow substantially with the increasing computer power and advancements in the development of force fields and enhanced MD methodologies.
- Molecular Dynamics Simulations
- drug development
1. Introduction
The purpose of a computer simulation is to gain insight into the behavior of an actual physical system or process. To achieve that specific objective, a model system is developed that represents or emulates the given physical system. A suitable algorithm subsequently generates a time series or an ensemble of states (“observations”) for the model system. Finally, an analysis is conducted by calculating various system properties from these states (certain properties may also be monitored during a simulation). In the present context, the word “simulation” usually refers to the process of generating states by numerically solving a set of differential equations for the selected degrees of freedom (state variables) of the given model system. Many computed system properties are measured by experiment as well so that an explanation of the observed experimental data is immediately available based on the model system and the simulation results. More importantly, one can also observe behavior that is inaccessible to experiment and test “what-if” scenarios (e.g., mutation studies). As a result, simulation techniques have become invaluable tools for modern research as they complement experimental approaches. With the continuing advance of computing power, such tools will only further increase in importance.
2. Classical Molecular Dynamics Simulations
Molecular dynamics (MD) is one such simulation technique [1][2][1,2]. It aims at deriving statements about the structural, dynamical, and thermodynamical properties of a molecular system. The latter is typically a biomolecule (solute) such as a protein, an enzyme, or a collection of lipids forming a membrane, immersed in an aqueous solvent (water or electrolyte). In the case of proteins and enzymes, the experimental protein structure as deposited in the Protein Data Bank (PDB) [3] serves as a starting point for MD simulations. If no structure is available, one must resort to modeling (predicting) the structure for which several techniques are available, such as homology or comparative modeling [4]. In atomistic “all-atom” MD (AAMD), the model system consists of a collection of interacting particles represented as atoms, describing both solute and solvent, placed inside a sufficiently large simulation box, where their movements are described by Newton’s laws of motions. An algorithm such as velocity-Verlet or leap-frog [2] is employed to advance over the course of many time steps the state of the model system as a function of time (see FigureFigure 1 1 for a schematic view of a basic MD algorithm). A single state consists of the combined values of the atoms’ positions and velocities (or momenta). To advance the state, forces acting on particles are computed from a model or empirical potential energy (“force field”), a function of particle positions, which includes all types of “non-bonded” interactions, such as electrostatic and Lennard-Jones forces, but also various types of “bonded” potentials for preserving the structural integrity of the given biomolecular system. The latter include harmonic potentials for maintaining bonds, bond angles, and “improper” dihedrals as well as terms for dihedrals. Some force fields include the Morse potential for a more realistic representation of bonds, while others may account for explicit electronic polarization effects. An extensive discussion of force fields is given by Monticelli and Tieleman [5]. Of note, various force fields have been developed for different types of molecules. In the context of our review, force fields for proteins [5], biological lipids [6], and small molecules [7] are of particular relevance (see TableTable 1 1 for examples of current commonly used force fields). Force fields are also employed to compute energies in molecular mechanics (MM) applications [8]. Such simulations are usually conducted under conditions of constant temperature and pressure to mimic laboratory conditions for which special algorithms are available. In addition, to emulate a very large molecular system, several techniques for artificially extending the size of the model system have been developed. The most common one is the periodic boundary condition (PBC). Here, an infinite number of replicas of the central simulation box surrounds the central box. Due to the long-range character of electrostatic interactions, special techniques such as Ewald-based methods are required to include the interactions between the particles in the central box and their replicas. In the course of a simulation, successive states at regular time intervals are stored in a trajectory for later analysis. Typically, in AAMD, the time step is 1–2 fs (1 fs = 10–15 s) and the system size is in the order of tens of thousands of atoms (including solvent). A larger number of software packages for MD of biomolecules are available, for example, GROMACS [9], AMBER [10], NAMD [11], and CHARMM [12].
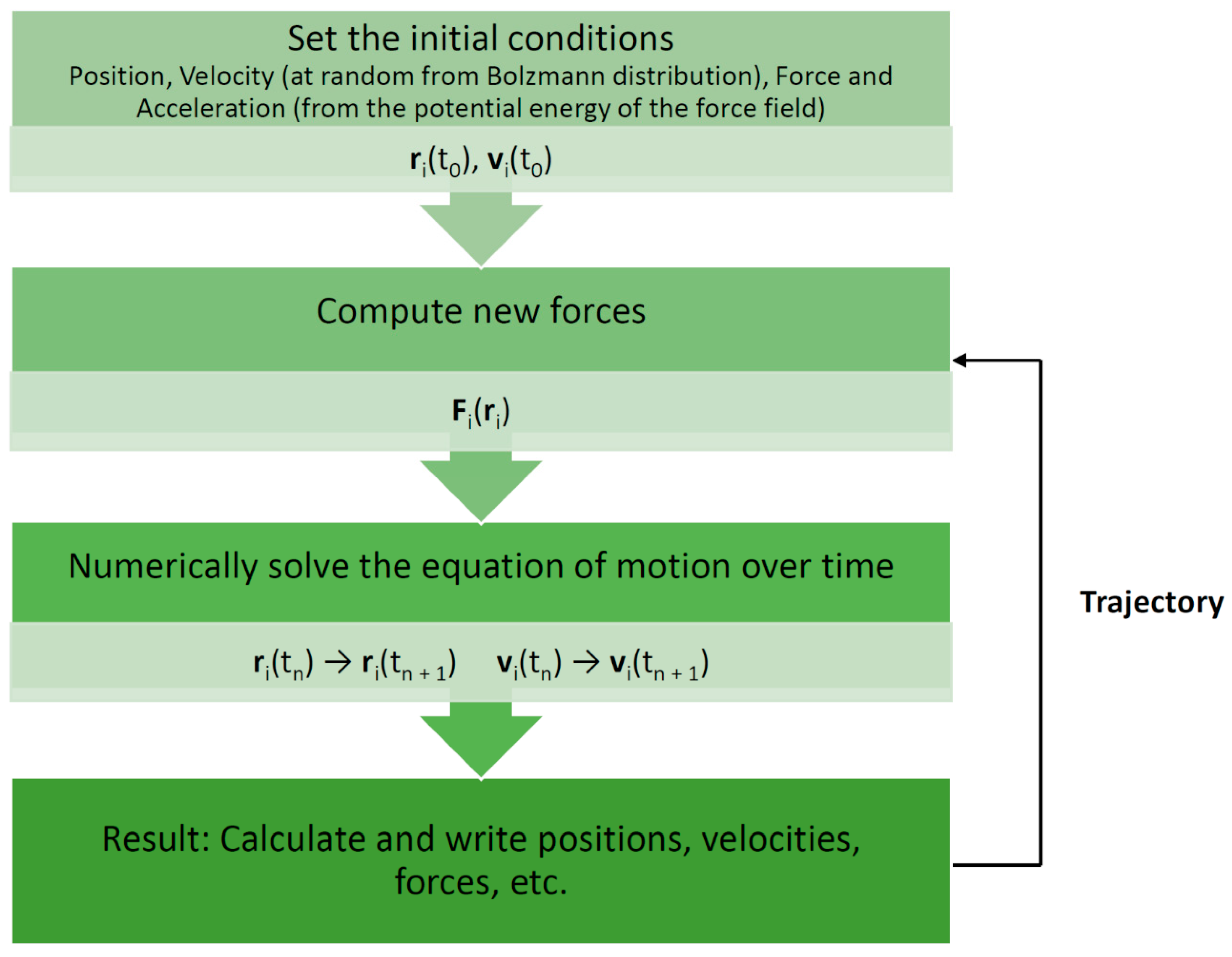
Table 1. Examples of commonly used force fields in molecular dynamics simulations.
| Type of Molecule | Force Field | |||||||
|---|---|---|---|---|---|---|---|---|
| Protein | AMBER [14], CHARMM [15], GROMOS [16], OPLS-AA [17] | |||||||
| Small organic molecule | General AMBER Force Field (GAFF) [18], CHARMM General Force Field (CGenFF) [19], Merck Molecular Force Field (MMFF) [20][21][22][23][24], OPLS3 [25], GROMOS96 [2628][29] | General AMBER Force Field (GAFF) [18], CHARMM General Force Field (CGenFF) [19], Merck Molecular Force Field (MMFF) [20,21 | ][ | ,22 | 27] | ,23 | [ | ,24], OPLS3 [25], GROMOS96 [26,27,28,29] |
| Lipid | GROMOS (45A3, 53A6, 54A7/8) [30]; Berger lipid FF [31]; CHARMM (C36 lipid FF [32], C36-UA [33]); Slipids FF [34]; AMBER (LIPID14 FF) [35] |
Early applications of AAMD were concerned with rather simple systems such as liquid argon consisting of just 864 atoms [36] and covered the ps (10−12 s) time scale. The first MD simulation of a biomolecule was achieved by McCammon et al. in 1977; bovine pancreatic trypsin inhibitor (58 residues) was simulated for 9.2 ps [37]. Nowadays, µs (10−6 s) timescale is easily achieved with relatively small proteins [38], wherewith larger systems, this is reachable if state-of-the-art computational power is available [39]. More typically, MD of larger biomolecular systems attain hundreds to thousands of ns (10−9 s). MD excels in focusing on the dynamical aspects of a given protein or enzyme in relation to its function. Applications include, for instance, estimation of affinities ∆bG⊖ (the standard Gibbs free energy of binding) of ligands for proteins using the so-called free energy perturbation (FEP) methods [40], the inclusion of charge fluctuations in constant pH AAMD [41], folding of small proteins [42], and the simulation of ion channels [43]. Additional examples are also listed in the recent reviews by Cavalli and collaborators [44] and Hollingsworth and Dror [45]. Recently, one of the largest atomistic simulations was reported by Rommie Amaro’s group where they simulated an explicitly solvated influenza A viral envelope in a phospholipid bilayer [46], a system of ca. 160 million atoms, for approximately 121 ns. Another study by Jung et al. reported the first atom-scale simulation of an entire gene with a billion atoms [47].
It is worthwhile to stress that MD is meant to explore the configuration space (the set of all values of positions and momenta). In the widely used ligand-protein docking one also needs to sample the configuration space using a similar force field as in MD in order to optimize the location and binding mode (a “pose”) of the ligand on the surface of a given protein (receptor) [48]. However, the sampled configuration space is frequently restricted to a specific region of the protein, while also only specific portions of the protein and/or ligand are allowed to fluctuate (e.g., only the protein’s side chain are displaceable, while the main chain is kept rigid). The outcome of such docking studies is a small set of possible complexes, typically ranked according to the force field employed. Dynamical information is not obtained from ligand-protein docking studies, but some measure for the affinity of the ligand for the protein may be obtained. In fact, the lack of a proper description of systems’ true dynamics is one of the biggest caveats of docking [49]. Therefore, frequently after selecting one of the complexes (usually the highest-ranked complex), an MD simulation is conducted to explore the complex in much greater detail [50].
3. MD simulations in drug discovery and development
Over the past 50 years, MD simulation techniques have established their relevance in modern drug discovery and development processes. With the increasing computer power and development of new force fields and enhanced sampling methods, it is now possible to simulate even big and complex (bio)molecular systems in time scales that can give important insights into real-life molecular events and interactions. MD simulations can be successfully used to uncover the conformational dynamics of highly flexible target proteins, thus providing valuable insights for drug discovery and design. Moreover, MD-generated conformational ensembles can be helpful in ligand design against extremely flexible intrinsically disordered proteins. Enhanced MD approaches and force field development are key in tackling such challenging targets. MD simulations can also reveal important details of antibody-antigen interactions and help design novel antibody therapeutics with improved properties.
MD-based binding free energy calculations are widely used in the hit identification phase to improve the accuracy of ranking the putative hits. In addition, the design of drugs with improved binding kinetics benefits from various enhanced MD techniques that probe the drug residence times at the target site. Similarly, MD simulations can facilitate peptide docking by enhancing the conformational sampling and refinement of peptide-protein complexes in the development of peptide therapeutics.
MD simulations of membrane proteins embedded in a relevant cell membrane model have been challenging due to the big size of the simulation system, but especially coarse-graining has helped to reduce the computational cost. Inclusion of the membrane in MD simulations has revealed important insights into lipid-protein interactions, the function of membrane proteins, as well as the ligand entry and exit into the target binding site.
Apart from the first steps of the drug discovery process, MD simulations have also shown to be useful in pharmaceutical development and formulations studies. For example, crystalline and amorphous drugs, drug-polymer formulations, or drug-loaded nanoparticles can be studied by MD simulations to complement experimental studies. Molecular-level insights into such systems can help in improving the solubility, stability, or other properties of drug formulations.
4. Conclusion
In conclusion, MD simulations can serve as a powerful tool in facilitating the early phases of the modern drug discovery and development process. In the future, MD simulations will likely gain even more importance due to the theoretical and technological advancements in the field.
