2.1. Filtration Process

Filtration is one of the core processes in water treatment. The term refers to the removal, mainly by physical action, of suspended solids as the suspension flows through a bed packed by granular media. If a coagulant is added, colloids can be removed at the same time and the range of detained particles increases considerably. Filtration focuses mainly on turbidity, colour, microorganisms and particulates, whether already present in the water or formed via pre-treatment ^[4][5][4,5]. The particles involved are considerably smaller than the grain size, as shown on the right-hand side of Figure 1.

Figure 1. Range of effectiveness of the treatment processes (re-prepared using the data from ^[6]).

Range of effectiveness of the treatment processes (re-prepared using the data from [6]).

Filter efficiency is determined by physical characteristics, such as grain size, shape, porosity, and bed depth/media grain size ratio. McGivney and Kawamura [7] suggest using L/de ratio for the design of filter beds where L is the depth of the filter bed (mm) and de is the effective size of the filter medium. L/de ranges between 1000 and 2000 for different filter beds—1000 for ordinary mono-medium sand and dual media beds, 1250 for regular tri-media beds (coal, sand, and garnet), 1250 to 1500 for coarse deep mono-medium beds in which de is 1.2 to 1.4 mm, and 1500 to 2000 for very coarse mono-medium beds in which de is 1.5 to 2.0 mm. It is also emphasized that pilot studies are recommended in the selection of filter depths when the medium is larger than 1.5 mm. The same authors [7] also recommend using L/de ratios that are increased by 15% to achieve filtered water turbidity less than 0.1 Nephelometric Turbidity Unit (NTU).

Filtration might occur as depth or as cake filtration. In the former, particles are caught in the pore system of the medium via attachment, while the second one involves the creation of a "“cake"” on the surface of the medium, with most solids being removed on the top [4]. Granular media filters act through depth filtration, with the majority of the filter media involved [8].

The filtration process consists of a transport stage, which takes particles closer to the filter media and an attachment stage that depends upon particle–surface interactions. As attachment mechanisms might cause the deviation of particles towards the surface of the grain, the two stages are not completely distinct ^[9][10][9,10]. Some authors, however, tend to discard the influence of surface forces when compared to the effect of transport mechanisms [11]. Particles might also undergo aggregation; they can form clusters that are more easily transported and deposited on the medium. Detachment is considered to be additional stage as well, causing particles to re-join the flow ^[12][13][12,13].

The study of deep bed filtration has relied on the interpretation of the filter bed as a group of single collectors; the efficiency is calculated considering the bed to be composed of uniform spheres acting as collectors [14]. The removal at any given plane at a certain distance from the surface of the media will be a function of the number of collectors located within that distance. This transforms the problem into transport and deposition of particles onto individual grains (trajectory analysis or microscopic model) [15]. The trajectory analysis is, however, valid only for a clean filter; the deposition of particles will vary the characteristics of the filter bed and the flow pattern. Removed particles will act as additional collectors for the particles subsequently reaching the bed [16]; their effect has to be included when calculating the efficiency. Some authors argue that these additional collectors can be more effective than the filter grains themselves [17].

During the process, several stages can be recognised (Figure 2). According to Jegatheesan et al. [10], an initial stage might be identified when the filter is still clean, followed by a second transient stage. During the transient stage, the filter performance is at first improved (ripening), then maintained throughout a subsequent working stage, and it finally deteriorates during breakthrough. The improvement in the performance is due to the increased deposit, which leads, in time, to an increase in the velocities and a decrease in the deposition. When breakthrough occurs, an insufficient depth of filter bed is available for removal and the run has to be terminated. The majority of authors, however, dismiss the initial stage as not being part of the average filtration run, thus taking into account only the three parts in which the transient stage is divided [18].

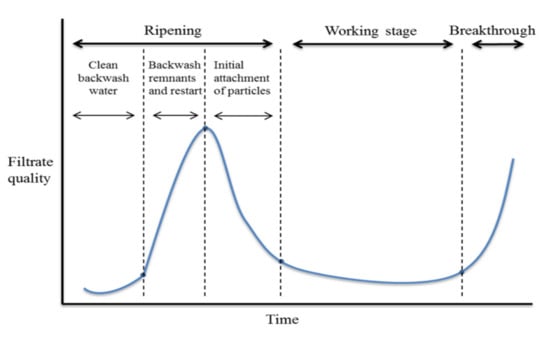
Figure 2. The filter cycle (reprepared using the data from [19]).

On the other hand, the macroscopic model does not take the transport/attachment problem into consideration. The overall removal is obtained via the integration of a mass balance relating the particle concentration to time and the kinetic equation relating the variation in concentration to the filter depth.

Transport in aqueous solutions involves multiple mechanisms (Figure 3) in a laminar flow. The occurrence of each mechanism depends upon the particle size. If the particle size is larger than the void size, straining is involved; for smaller particles sedimentation, interception and diffusion are dominant. The latter is more relevant for particles below 1 µm, while sedimentation and interception involve particles above 1 µm. Yao et al. [20], while modelling filter efficiency as a function of the particle size of contaminants, concluded that, for particles over 1 µm, the transport efficiency increases with the particle size, while for lower values it increases with decreasing particle size. A minimum is reached around 1 µm, a size that tends not to be removed during the run [17]. Among the protozoa Giardia Lamblia and Cryptosporidium Parvum, the former (10–15 µm size) is successfully removed by sedimentation. Cryptosporidium, ranging between 3 and 5 µm, is closer to the values of minimum transport efficiency ^[16][20][16,20].

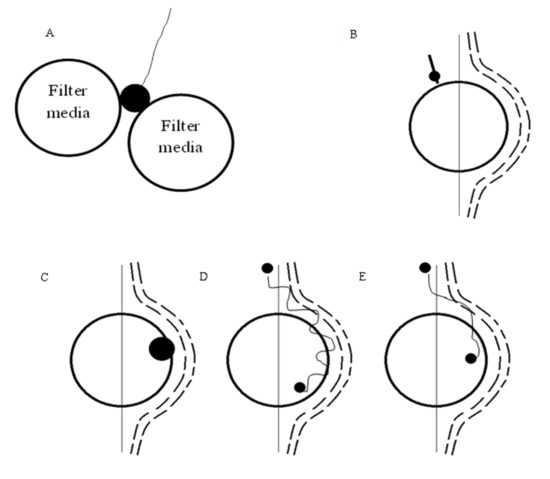
Figure 3. Transport mechanisms in water filtration: (A), straining; (B), sedimentation; (C), interception; (D), diffusion; (E), hydrodynamic (reprepared using the data from ^[10][12][20][10,12,20]).

The following mechanisms have been described in the literature:

• Straining. It is not desirable as collected particles clog the upper part of the bed (blinding), preventing an efficient use of the filter ^[12].

• Sedimentation. This is favoured when the density of the suspended material is greater than that of water. The particle will deviate from the streamline because of gravity and it will impact the medium surface ^[12][20]. This depends upon particle density and temperature ^[16], the diameter of the particle and more generally on the ratio between the settling velocity of the particle and the velocity of the fluid approaching the media ^[12]. Larger particles and lower filtration velocities will lead to higher collection efficiency for this mechanism ^[9].

• Interception. This occurs when a particle is transiting within a distance equal to its radius from the surface of the grain. The contact between the particle and the grain can result in attachment (12). The mechanism is very similar to straining, but smaller particles are involved ^[6][12][21]; it depends on the ratio of the particle diameter to the media diameter ^[12]. Its efficiency increases with increasing particle size and decreasing collector size ^[9].

• Diffusion. This is due to the thermal energy of the fluid, which is transferred to the particles. This causes them to drift from the streamlines to impact the surface of the grain or on other particles ^[9]. As mentioned previously, diffusion is efficient for sizes below 1 µm because viscous drag is not restricting the particles; the lower the particle size, the more significant the mechanism ^[12].

• Ives ^[12] adds inertia. The streamlines tend to diverge from the grains when approaching them, but particles with sufficient inertia might proceed unchanged and impact on the grains. It is, however, negligible for water filtration because of small mass and density differences ^[12][22].

• Furthermore, every particle is subjected to hydrodynamic action, caused by the velocity gradients within pore openings. As it experiences higher velocities on one side, the particle tends to rotate and create an additional spherical field, which causes the particle to move across the flow field. Because of deformable non-spherical shapes and non-ideal flow conditions, the results are non-predictable random paths, leading to movement across the streamlines and collision with the grains ^[12][23]. This is usually negligible; however, it appears to be more effective for lower particle–grain size ratios ^[11].

• Straining. It is not desirable as collected particles clog the upper part of the bed (blinding), preventing an efficient use of the filter [12].

• Sedimentation. This is favoured when the density of the suspended material is greater than that of water. The particle will deviate from the streamline because of gravity and it will impact the medium surface [12,20]. This depends upon particle density and temperature [16], the diameter of the particle and more generally on the ratio between the settling velocity of the particle and the velocity of the fluid approaching the media [12]. Larger particles and lower filtration velocities will lead to higher collection efficiency for this mechanism [9].

• Interception. This occurs when a particle is transiting within a distance equal to its radius from the surface of the grain. The contact between the particle and the grain can result in attachment (12). The mechanism is very similar to straining, but smaller particles are involved [6,12,21]; it depends on the ratio of the particle diameter to the media diameter [12]. Its efficiency increases with increasing particle size and decreasing collector size [9].

• Diffusion. This is due to the thermal energy of the fluid, which is transferred to the particles. This causes them to drift from the streamlines to impact the surface of the grain or on other particles [9]. As mentioned previously, diffusion is efficient for sizes below 1 µm because viscous drag is not restricting the particles; the lower the particle size, the more significant the mechanism [12].

• Ives [12] adds inertia. The streamlines tend to diverge from the grains when approaching them, but particles with sufficient inertia might proceed unchanged and impact on the grains. It is, however, negligible for water filtration because of small mass and density differences [12,22].

• Furthermore, every particle is subjected to hydrodynamic action, caused by the velocity gradients within pore openings. As it experiences higher velocities on one side, the particle tends to rotate and create an additional spherical field, which causes the particle to move across the flow field. Because of deformable non-spherical shapes and non-ideal flow conditions, the results are non-predictable random paths, leading to movement across the streamlines and collision with the grains [12,23]. This is usually negligible; however, it appears to be more effective for lower particle–grain size ratios [11].

Flocculation within the filter pores might also occur, increasing the removal possibility [12]. This does not constitute a proper transport mechanism and only contributes in a small measure.

It is important to stress that the mechanisms act simultaneously, so that the effective transport of a particle cannot be ascribed to a single one, but to all of them. However, when considering water filtration, straining does not give a consistent contribution to the removal because of the size of the pores in comparison to the size of the particles [16]. Diffusion is not very significant in conventional rapid filtration, as the chemical pre-treatment favours the aggregation of smaller particles [9]. If biologically active filters—such as slow sand and granular activated carbon (GAC)—are considered, biodegradation has to be included among the mechanisms. Moreover, GAC filters enable the adsorption of certain contaminants [24].

As the particle approaches the collector hydrodynamic retardation occurs. This is due to the resistance caused by the displacement of fluid ^[15][16][15,16]. This depends on the distance between particle and grain surface, tending towards infinity as the distance tends to zero. Hydrodynamic retardation is more relevant for large, less dense flocs and particles than for the smaller and denser ones [9].

While transport is mainly a physical step, attachment is mostly chemical and it requires previous destabilization [17]. It is a consequence of short-range surface forces, namely van der Waals, electric double-layer repulsion and hydration forces, and the principles of these forces can be found in the Supplementary Materials.

Filter effluent particles can be divided among influent particles that are never deposited and particles that detach after deposition [25]. Detachment has been identified as the major cause of the presence of particles in the effluent. This does not occur until a specific value of the deposit is reached; afterwards, it is concurrent with attachment reaching an equilibrium [18]. An increase in the flow rate might cause the detachment of those particles that are less strongly linked [22]; it is generally agreed, though, that the main cause of detachment is the increase in velocity within the pores due to the deposits [26]. This can also be due to the impact of incoming particles on unstable deposits [14]. Detachment occurs when the hydrodynamic force becomes greater than the adhesive force and it acts via three mechanisms; rolling, sliding and lifting. As rolling does not necessarily lead to detachment, sliding and lifting are considered to be the main mechanisms [26].

2.2. Filtration Operating Setup

Filtration can be performed in two different ways: either as direct filtration or as a more conventional approach, where it is preceded by coagulation and clarification; this is the custom for waters containing a high level of particulate matter. Direct filtration is placed directly after flocculation, so that there is no separate clarification step. Direct filtration should be applied only when the average turbidity does not exceed 10 NTU, with peaks below 40 NTU and total organic carbon (TOC) not above 2 mg/L [5]. Moreover, media with a large grain diameter have to be employed in order to decrease the head loss [27]. Polymers are generally used before direct filtration [1], but if metal salts are chosen, small doses should be used to obtain small filterable flocs [5]. O'’Melia [9] actually differentiates between contact (or in-line) filtration and direct filtration; in the former, the destabilized particles are directly sent to filtration, eliminating flocculation as well.

Additionally, filters can be classified in terms of continuous or semi-continuous operation, the latter being the case when the filter has to be put offline to be backwashed. The use of semi-continuous operation is the most common [28].

The process can be driven by gravitational force-rapid gravity filtration, or by pressure-pressure filtration. Both applications depend only upon physical removal [1]. The differences lie mainly in the pressure required, the filtration rate, and the type of vessel [29]. Pressure filters allow for significantly higher flow rates [8]. An additional type of filter; slow sand filtration, was historically the first one to be employed. It acts through a combination of straining and biological action [5]. Rapid sand filters were later favoured over slow sand because of the large area required by the latter to maintain a sufficient output and the excessively low filtration rates (0.1–0.3 m/h, or lower), also due to the smaller size of the sand grains [8]. Recently, it has been successfully adopted in many small communities because of the efficacy in removing protozoa pathogens ^[8][30][8,30]. Slow sand filtration is not, however, effective when dealing with high levels of turbidity and algae because of a limited removal ability and long ripening times ^[5][31][5,31]. It also shows low efficiency in removing organic material and for this reason the use of granular media amendments (such as granulated activated carbon (GAC), anthracite, etc.) has been proposed. Resins and GAC are effective but lead to an excessive head loss; the other options have not proven to be more efficient than conventional operations ^[4][31][4,31]. Today, the majority of filters are of the gravity type and pressure filters are partially used in small plants. Rapid gravity filtration has the advantage of employing higher rates than slow sand filtration and it can be employed in either a single media or a multimedia configuration, coupling different materials together to increase the efficiency.

Filtration configurations affect the filtration performance. As single sand medium filters cannot always perform adequately to achieve the treatment tasks, a solution was found in the introduction of dual media filters by placing a denser material at the bottom and a lighter one at the top, with decreasing size. In the most common configuration, a layer of anthracite is placed on top of a sand layer; in some cases, an additional layer of garnet is added ^[1][5][1,5]. The filtrate quality is comparable to that of sand, but filter runs can be up to 1.5–3-times longer with similar filtration rates. Attempts have also been made towards an increase in the filtration rate with dual configurations, though this is often accompanied by the use of coagulation aids. The size of the flocs, resulting from coagulation, is important when employing dual configurations. If the flocs are too small, they might bypass the first layer and lead to a fast clogging of the sand layer. If too large, the anthracite layer would be quickly clogged [5]. The effective size for anthracite is generally 1.5 mm, though varied values are obtained in different parts of the world. The depth of the anthracite layer is usually set around 150–300 mm, while for sand it is at 450–600 mm [32]; the opposite proportion is given by Binnie and Kimber [1].

Zouboulis [27] compared the performance of a single medium sand filter and a dual media sand/anthracite filter for conventional and direct filtration. During conventional filtration, the dual media configuration was able to operate for a longer cycle, leading to a 10% higher water production; the length of a dual media cycle was 2–3 times that of the single medium, with final head loss values being less than half (Figure 4a). For turbidity removal, both configurations showed values well below 0.2 NTU, with the dual media configuration performing marginally worse (Figure 4b). Direct filtration was more difficult to control. For small doses of coagulant, the single medium did not reach the required level of turbidity, presenting values of 0.5–1 NTU. The dual media filter was more effective, achieving turbidity values slightly higher than those with conventional operations (0.2–0.3 NTU) [27].

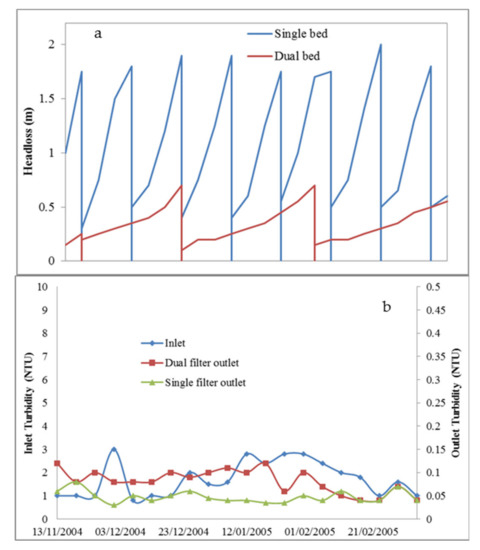
Figure 4. (a) Head loss development (19/02/2005–25/02/2005) and (b) values of turbidity for conventional treatment (reprepared using the data from [27]).

In order to adopt higher filtration rates, there has been an attempt to use anthracite in coarser mono-medium filters, with a deeper bed (1.8 m); though this route was soon abandoned [30]. The main issue with anthracite is its higher cost and the limited number of sources worldwide; for these reasons it has occasionally be replaced by high grade bituminous coal [5]. Other materials have been used in specific circumstances, such as GAC in place of anthracite or sand for the removal of odours. It is more common, however, to include an adsorption stage after the filter with a longer contact time that increases the efficacy of the GAC [30].

2.3. Process Performance Monitoring and Filter Backwash

Filtration performance can be monitored by regularly checking the flow rate, head loss development and effluent quality characteristics (e.g., turbidity). Flow rates vary depending upon the type of filter, the filtration media, the plant and the clarified water quality. Typical rates for deep coarse beds are around 6–8 m/h, though they can be increased up to 12–15 m/h if dual media filters are employed and the feed water shows consistent good quality [1]. The value 6–7 m/h should not be exceeded where there is a presence of oocysts in the raw water; for graded sand beds the rates applied should be 25% lower. Rapid changes in the rates are to be avoided, as they can lead to excessive shear on the deposits, with release of particles into the effluent [19]. It is observed that, at rates above 15 m/h, the quality of the water deteriorates, and above 20 m/h, the head loss development becomes too rapid [32]. Higher filtration rates imply a faster development of the head loss, but they give higher productivity, so that the ideal balance has to be found [14]. Clean bed head loss is the resistance initially encountered by the flow through the bed. The head loss development is linear if the entire depth of the bed is used, but exponential if only a small depth near the surface is used [23]. During operation it is important to avoid negative head, which is to say pressures below atmospheric pressure within the bed. This occurs when the head loss exceeds the static head (water depth) at any given depth [14]. Depending upon the media, this could occur at different points in the bed. The consequences might include the release of dissolved gases, poor effluent quality, premature ending of the run, cracking and mud ball formation ^[5][6][5,6].

Once the rate has been chosen, it can be applied in constant or declining mode. With declining rates, the amount of water fed to the filter is maintained throughout the run. Initially, when the filter is clean, a low head loss (0.2–0.3 m) is measured and the maximum flow is limited via a valve at the outlet. During the run the head loss increases and the flow rate diminishes, until the minimum acceptable flow rate is reached, or backwashing is scheduled. The main concern over this mode of operation is related to the negative effect of the high filtration rates at the start. Constant rate filtration is achieved by controlling the flow either at the inlet or the outlet. The head loss through the filter increases during the run but the flow remains unchanged. Backwashing is performed either when the terminal head loss or turbidity values are reached, or after a set operation time, generally 24–60 h ^[1][5][12][1,5,12]. It is desirable for the limiting head loss (1.5–2 m) to occur at the same time as the breakthrough, so as not to lose filtering capacity [12]. The safety of operations is, however, more important and it is preferable not to wait until the filters are close to breakthrough.

Figure 5 shows the filtrate turbidity during a typical rapid sand filter run. The filter is commonly allowed to reach a head loss of 2 m before being backwashed. The employment of rapid sand filters gives rise to a specific issue; during backwashing smaller particles would settle closer to the top while larger ones would reach the bottom of the filter, leading to stratification of the bed. The top, finer layer would retain the majority of incoming particles, with an ineffective use of the depth and shorter runs.

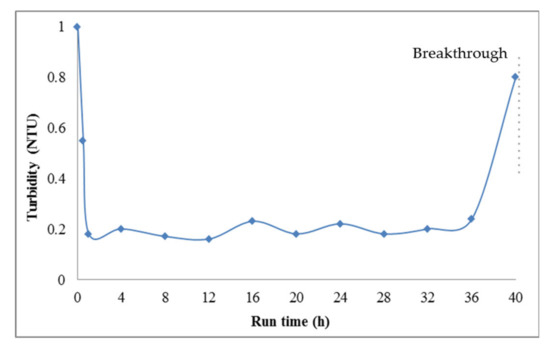
Figure 5. Turbidity as a function of run time for a typical filter run (reprepared using the data from ^[32]).

Turbidity as a function of run time for a typical filter run (reprepared using the data from [32]).

The backwash is performed by inverting clean water so that the filter is flushed. The rates applied are generally above the minimum fluidisation rate—i.e., the rate at which the drag forces overcome the weight of the grain and the bed starts to expand (be fluidised) [1]. This is affected by features of the media, such as size and density and by the packing of the bed; the lower the voidage, the lower the minimum fluidisation rate [33]. Voidage refers to the free space within the filter bed, which is available for the retention of solids [34]. There is also a significant temperature effect due to the influence of the viscosity of the water [6]. Employing the right backwashing rate is fundamental, as rapid flow might lead to loss of media and to an excessive consumption of water. Indeed, a variable amount of filtered water and the necessary pressure have to be provided; water consumption is usually around 2.5 times the bed volume [5]. Ineffective washing is the consequence of low backwash rates ^[6][33][35][6,33,35] together with floc build-up, which can lead to mud balls, jetting, cracks or shrinkage within the bed [5].

It is common to use air and water simultaneously, which has been demonstrated to be the most effective approach for backwashing, although the use of air scouring requires particular care as it could lead to modifications in the structure of the filter [33] and it increases the chances of media loss [19]. A backwashing procedure is described by Ratnayaka et al. [5] for a deep bed homogeneous sand filter with air (3–4 min) and water at a flow sufficient to achieve fluidisation (4–6 min), which is suggested as a practice suited to all rapid gravity filters. Full fluidisation of the bed at the end of the backwash is required if multimedia filters are being cleaned, as it allows proper re-stratification. In practice, intermixing at the interface occurs in most cases for a depth of 100–150 mm. It has been argued that this intermixing, by reducing the voidage of the coarser media, increases the filtrate quality and leads to higher head loss development [5]. The intermixing should not, however, occur for more than 20% of the layer [36], or a zone with extremely low permeability might form with risk of clogging [37].

According to some sources, rates should be around 10–30 m/h for the water flow, while airflow rates can be between 50–80 m/h [1]; others recommend a value between 23 and 58 m/h for the air flow, and 7–25 m/h for the wash with water [32]. During the first few backwashes, it is likely that a certain number of fine grains will be removed from the bed. This might affect the packing of the bed, so that adjustments to the process and the flow rates are required [33]. A solution to avoid negative effects is the addition of 30 to 50 mm of media to the bed depth [29]. Media losses are more common for anthracite and GAC, due to their lower attrition resistance [38]. If the issue is prolonged after the first few cycles, this might signify that the rates applied are too high, or that the filter does not possess the required characteristics [4].

One of the main concerns related to backwashing is the high level of turbidity after the filter has been returned to service. This phase is referred to as ripening (Figure 2). This is due to the removal of particles that contribute to filtration and to flocs not properly discharged during the last backwashing phases [32]. Three stages have been identified; initially, the filtrate is affected by the remaining backwash water located in the underdrains of the filter and subsequently by contaminants left above and within the bed.

It should be noted that the effectiveness of filtration is reduced because of the lack of the additional collection capability due to retained particles [39]. This issue has received increasing attention as it has been shown that the transmission of Giardia and Cryptosporidium cysts can occur during this phase [16]. Different techniques are available to minimize the issue; the addition of a coagulant to the backwash water or to the influent as the filter is returned to service, implementation of a terminal sub-fluidised rinse, filter resting (delayed start), discard of the first fraction of effluent (filter-to-waste) and variation of filter rates (starting from low rates and gradually increasing; called slow start) ^[5][24][5,24]. It is considered normal for a filter to produce effluent with a turbidity of 0.5–1 NTU after being returned to service, though it should then decrease to 0.2 or less in the first 30 min of operation and to 0.1 after an additional hour ^[1][8][1,8]. Hess [19] reports the objective of 0.3 NTU after backwashing and below 0.1 NTU within 15 min of the return to service.

3. Induction onf Mathematicals Models for the Bed Media Filters

Many mathematical models have been developed to predict and evaluate the granulated media

filters performance. The model from Mintz [40] and Ives [41] describes the entire filtration cycle using

empirical functions derived from bench scale experiments and partial differential equations.

Additionally, the model from O'’Melia and Ali [42] describes the clean bed filter performance and the

ripening stage, which is based on calculations of particle volume balances, applied to a given filter

bed depth without considering the entire filtration cycle. Both models did not consider the deposit

porosity. On the other hand, the model by Adin and Rebhun [43] describes the bed retention ability

and the clogging process during the entire filtration cycle using the bed capacity expressed in weight

of accumulated material per unit of bed volume (the specific deposit), and bed hydraulic conductivity

expressed in velocity terms.

Using their microscopic model [44] and modifying the model by Adin and Rebhun [43],

Vigneswaran and Chang [45] developed a model to describe the entire filtration cycle with

experimental results. The model is mainly based on the detachment of deposited particles and on the

concept that there exists a maximum limit on particle deposition on the filter grain. Further

development of it was the models by Mackie [46], Hunt [47] and Boller and Kavanaugh [48] which

express the size-density relationships for aggregated particulate and describes the accumulation of

particulate deposits in the pore space of granular media filters. Goodarz [49] used the floc sizedensity

relationship for homogeneous particles and a head loss expression to present the effects of

particle size, particle density, filtration rate and media grain size on head loss development during inline

filtration. For the models to evaluate the deep bed filtration of waste water effluent, few cases

emphasized the relation between filtration parameters and sizes of particles in the deposit, though the

work by Cikurel et al [50] used existing filtration models to calculate and compare size density and

attachment strength of filter deposits, which were produced by the interaction of effluents with

primary flocculants and flocculation aids and the filter media during the contact filtration. They

found that in order to obtain an effective removal of particles without causing excessive pressure

gradients, a correlation must be established for the floc size, density, and strength, and filtration

parameters such as bed characteristics and approach velocity.

Development of mathematical models is one of important aspects in the fields of

filtration for water and waste water treatment, which should constitute to an independent

review and one of such comprehensive reviews can be read in [51]. Efforts are still under way to

develop a model that can describe the entire filter cycle and to accurately predict filtration

performance; since "“the long history in the deep bed filtration research would definitely make this an

achievable task in the future"” [51].

References

1. Binnie, C.; Kimber, M. Basic Water Treatment, 5th ed.; ICE Publishing: London, UK, 2013.
2. LeChevallier, M.W.; Au, K.K. Water Treatment and Pathogen Control—Process Efficiency in Achieving Safe Drinking Water; WHO Drinking Water Quality Series, IWA Pub., London: 2004.
3. Ritson, J.P.; Graham, N.J.D.; Templeton, M.R.; Clark, J.M.; Gough, R.; Freeman, C. The impact of climate change on the treatability of dissolved organic matter (DOM) in upland water supplies: A UK perspective. Total Environ. 2014, 473–474, 714–730.
4. Cheremisinoff, N.P. Handbook of Water and Wastewater Treatment Technologies; Butterworth-Heinemann: Oxford, UK, 2002.
5. Ratnayaka, D.D.; Brandt, M.J.; Johnson, K.M. Twort’s Water Supply, 6th ed.; Butterworth-Heinemann: Oxford, MA, USA, 2009.
6. Tebbutt, T.H.Y. Principles of Water Quality Control, 5th ed.; Butterworth-Heinemann: Oxford, UK, 1998.
7. McGivney, W.; Kawamura, S. Cost Estimating Manual for Water Treatment Facilities; John Wiley & Sons, Inc. New Jersey 2008.
8. Gray, N.F. Water Technology, 3rd ed.; IWA Pub., London: 2010.
9. O’Melia, C.R. Particles, Pretreatment and Performance in water filtration. Environ. Eng. 1985, 111, 874–890.
10. Jegatheesan, V.; Vigneswaran, S. Deep Bed Filtration: Mathematical Models and Observations. Rev. Environ. Sci. Technol. 2005, 35, 515–569.
11. Ison, C.R.; Ives, K.J. Removal mechanisms in deep bed filtration. Eng. Sci. 1969, 24, 717–729.
12. Ives, K.J. Rapid Filtration. Water Res. 1970, 4, 201–223.
13. Zamani, A.; Maini, B. Flow of dispersed particles through porous media—Deep bed filtration. Pet. Sci. Eng. 2009, 69, 71–88.
14. Cleasby, J.L.; Logsdon, G.S. Granular bed and precoat filtration. In Water Quality and Treatment: A Handbook of Community Water Supplies; Letterman, R.D., Ed.; McGraw-Hill, New York: 1999.
15. Rajagopolan, R.; Tien, C. Single collector analysis of collection mechanisms in water filtration. J. Chem. Eng. 1977, 55, 246–255.
16. Amirtharajah, M. Some theoretical and conceptual views of filtration. Am. Water Works Assoc. 1988, 80, 36–46.
17. O’Melia, C.R.; Ali, W. The role of retained particles in deep bed filtration. Water Technol. 1978, 10, 167–182.
18. Han, S.; Fitzpatrick, C.; Wetherill, A. Mathematical modelling of particle removal and head loss in rapid gravity filtration. Sci. Technol. 2008, 43, 1798–1812.
19. Hess, A.; Logsdon, G.S.; Chipps, M.J.; Rachwal, A.J. Filter Maintenance and Operations Guidance Manual; AWWA Research Foundation and American Water Works Association: Denver, CO, USA, 2002.
20. Yao, K.-M.; Habibian, M.T.; O’Melia, C.R. Water and waste water filtration. Concepts and applications. Sci. Technol. 1971, 5, 1105–1112.
21. Stevenson, D.G. Flow and filtration through granular media—The effect of grain and particle size dispersion. Water Resour. 1997, 31, 310–322.
22. Ives, K.J. Filtration of Clay Suspensions through Sand. Clay Miner. 1987, 22, 49–61.
23. Ives, K.J. Capture mechanisms in filtration. In The Scientific Basis of Filtration; Noordhoff: Leyden, The Netherlands, 1975.
24. Castro, K.; Ahmed, R. Filtration. In Operational Control of Coagulation and Filtration Processes—Manual of Water Supply Practices, M37, 3rd ed.; American Water Works Association (AWWA), Denve: 2011.
25. Kim, J.; Tobiason, J. Particles in filter effluent: The roles of deposition and detachment. Sci. Technol. 2004, 38, 6132–6138.
26. Bai, R.; Tien, C. Particle detachment in deep bed filtration. Colloid Interface Sci. 1997, 186, 307–317.
27. Zouboulis, A.; Traskas, G.; Samaras, P. Comparison of single and dual media filtration in a full-scale drinking water treatment plant. Desalination 2007, 213, 334–342.
28. Asano, T.; Burton, F.; Leverenz, H. Removal of Residual Particulate Matter. In Water Reuse: Issues, Technologies and Application; McGraw-Hill, New York: 2007.
29. Voutchkov, N. Considerations for selection of seawater filtration pretreatment system. Desalination 2010, 261, 354–364.
30. Logsdon, G.S.; Horsley, M.B.; Freeman, S.D.N.; Neemann, J.J.; Budd, G.C. Filtration processes—A distinguished history and a promising future. Am. Water Works Assoc. 2006, 98, 150–162.
31. Collins, M.R.; Eighmy, T.T.; Fenstermacher, J.M.; Spanos, S.K. Using granular media amendments to enhance NOM removal. Am. Water Works Assoc. 1996, 88, 48–61.
32. Twort, A.C.; Ratnayaka, D.D.; Brandt, M.J. Water Supply, 3rd ed.; Butterworth-Heinemann: Oxford, MA, USA, 2000.
33. Fitzpatrick, C. Media properties and their effect on filter performance and backwashing. Water Sci. Technol. 1998, 38, 105–111.
34. Stevenson, D.G. The specification of filtering materials for rapid-gravity filtration. Inst. Water Environ. Manag. 1994, 8, 527–533.
35. Stevenson, D.G. Process conditions for the backwashing of filters with simultaneous air and water. Water Res. 1995, 29, 2594–2597.
36. Morgeli, B.; Ives, K.J. New media for effluent filtration. Water Res. 1979, 13, 1001–1007.
37. Ives, K.J. Specification for granular filter media. Water Treat. J. 1975, 15, 296–305.
38. Humby, M.S.; Fitzpatrick, C.S.B. Attrition of granular filter media during backwashing with combined air and water. Water Res. 1996, 30, 291–294.
39. Slavik, I.; Jehmlich, A.; Uhl, W. Impact of backwashing procedures on deep bed filtration productivity in drinking water treatment. Water Res. 2013, 47, 6348–6357.
40. Mintz, D.M. Modern Theory of Filtration. International Water Supply Ass, 7th Cong. Vol.1 . Special Subject
    
    No. 10 (Oct. 1966).
41. Ives, K. J. Theory of Filtration. International Water Supply Ass, Vienna. (1969).
42. O’Melia, C.R.; Ali, W. The role of retained particles in deep bed filtration, Prog. Water Technol., 1978, 10,
    
    167-182.
43. Adin, A.; Rebhun, M. A model to predict concentration and head-loss profiles in filtration. J. AWWA.
    
    1977, 8, 444-451.
44. Vigneswaran, S.; Chang, J.S. Mathemathical modelling of the entire cycle of deep bed filtration. Wat. Air
    
    Soil Pollut. 1986, 29, 155-164.
45. Vigneswaran, S.; Chang, J.S. Experimental Testing of Mathematical Models Describing the Entire Cycle of
    
    Filtration, Water Res. 1989, 23, 1413-1421.
46. Mackie, R.I. Numerical solution of the filtration equations for polydisperse suspensions. 6th World
    
    Filtration Congress, Nagoya, Japan, pp. 244-247 (1993).
47. Hunt J. The accumulation of solids within deep bed filters. 6th World Filtration Congress, Nagoya, Japan.
    
    pp. 236-239 (1993).
48. Boller, M.A.; Kavanaugh, M.C. Particle characteristics and headloss increase in granular media filtration.
    
    Water Res. 1995, 29, 1139-1149.
49. Goodarz-Nia, I. Floc density, porosity and void ratio in colloidal systems and aerosols. J. Coll. Interface Sci.,
    
    1977, 62, 131-141.
50. Cikurel, H.; Rebhun, M.; Amirtharajah, A.; Adin, A. Wastewater effluent reuse by in-line flocculation
    
    filtration process. Water Sci. Technol. 1996, 33, 203–211.
51. Jegatheesan, V.; Vigneswaran, S. Deep bed filtration: mathematical models and observations. Critical
    
    Reviews in Environ. Sci. Technol. 2005, 35, 515–569.