Robust Outlier-Adaptive Filtering

Robust Outlier-Adaptive Filtering: Comparison

Please note this is a comparison between Version 1 by Kyuman Lee and Version 2 by Camila Xu.

With the advent of unmanned aerial vehicles (UAVs), a major area of interest in the research field of UAVs has been vision-aided inertial navigation systems (V-INS). In the front-end of V-INS, image processing extracts information about the surrounding environment and determines features or points of interest. With the extracted vision data and inertial measurement unit (IMU) dead reckoning, the most widely used algorithm for estimating vehicle and feature states in the back-end of V-INS is an extended Kalman filter (EKF). An important assumption of the EKF is Gaussian white noise. In fact, measurement outliers that arise in various realistic conditions are often non-Gaussian. A lack of compensation for unknown noise parameters often leads to a serious impact on the reliability and robustness of these navigation systems. To compensate for uncertainties of the outliers, we require modified versions of the estimator or the incorporation of other techniques into the filter. The main purpose of this paper is to develop accurate and robust V-INS for UAVs, in particular, those for situations pertaining to such unknown outliers. Feature correspondence in image processing front-end rejects vision outliers, and then a statistic test in filtering back-end detects the remaining outliers of the vision data. For frequent outliers occurrence, variational approximation for Bayesian inference derives a way to compute the optimal noise precision matrices of the measurement outliers. The overall process of outlier removal and adaptation is referred to here as “outlier-adaptive filtering”. Even though almost all approaches of V-INS remove outliers by some method, few researchers have treated outlier adaptation in V-INS in much detail. Here, results from flight datasets validate the improved accuracy of V-INS employing the proposed outlier-adaptive filtering framework.

V-INS
UAV
EKF
IMU
camera vision
computer vision
image processing
outlier rejection
adaptive filtering
sensor fusion
navigation

^[1][2][3]

1. Introduction

The most widely used algorithms for estimating the states of a dynamic system are a Kalman Filter [

] and its nonlinear versions such as an extended Kalman filter (EKF) [

]. After the NASA Ames Research Center implemented the Kalman filter into navigation computers to estimate the trajectory of the Apollo program, engineers have developed a myriad of applications of the Kalman filter in navigation system research areas [

]. For example, Magree and Johnson [

] developed a simultaneous localization and mapping (SLAM) architecture with improved numerical stability based on the UD factored EKF, and Song et al. [

] proposed a new EKF system that loosely fuses both absolute state measurements and relative state measurements. Furthermore, Mostafa et al. [

] integrated radar odometry and visual odometry via EKF to help overcome their limitations in navigation. Despite the development of numerous applications of the Kalman filter in various fields, it suffers from inaccurate estimation when required assumptions fail.

Estimation using a Kalman filter is optimal when process and measurement noise are Gaussian. However, sensor measurements are often corrupted by unmodeled non-Gaussian or heavy-tailed noise. An abnormal value relative to an overall pattern of the nominal Gaussian noise distribution is called an outlier. In other words, in statistics, an outlier is an observation that deviates so much from other observations as to arouse suspicion that it is generated by a different mechanism [

9]. Such outliers have many anomalous causes. They arise due to unanticipated changes in system behavior (e.g., temporary sensor failure or transient environmental disturbance) or unmodeled factors (e.g., human errors or unknown characteristics of intrinsic noise). As an example of measurement outliers in many navigation systems, either computer vision data contaminated by outliers or sonar data corrupted by phase noise lead to erroneous measurements. Process outliers also occur by chance. Inertial measurement unit (IMU) dead reckoning and wheel odometry as a proxy often generate inaccurate dynamic models in visual-inertial odometry (VIO) and SLAM algorithms, respectively. Without accounting for outliers, the accuracy of the estimator significantly degrades, and control systems that rely on high-quality estimation can diverge.

]. Such outliers have many anomalous causes. They arise due to unanticipated changes in system behavior (e.g., temporary sensor failure or transient environmental disturbance) or unmodeled factors (e.g., human errors or unknown characteristics of intrinsic noise). As an example of measurement outliers in many navigation systems, either computer vision data contaminated by outliers or sonar data corrupted by phase noise lead to erroneous measurements. Process outliers also occur by chance. Inertial measurement unit (IMU) dead reckoning and wheel odometry as a proxy often generate inaccurate dynamic models in visual-inertial odometry (VIO) and SLAM algorithms, respectively. Without accounting for outliers, the accuracy of the estimator significantly degrades, and control systems that rely on high-quality estimation can diverge.

This paper presents improving the use of outlier removal techniques in image processing front-end and the development of a robust and adaptive state estimation framework for V-INS when frequent outliers occur. For outlier removal in the image processing front-end of V-INS, feature correspondence constitutes the following three steps: tracking, stereo matching, and 2-point RANSAC. To estimate the states of V-INS in which vision measurements still contain remaining outliers, we propose a novel approach that combines a real-time outlier detection technique with an extended version of the ORKF in the filtering back-end of V-INS. Therefore, our approach does not restrict noise at either a constant or Gaussian level in filtering. The testing results of benchmark flight datasets show that our approach leads to greater improvement in accuracy and robustness under severe illumination environments.

Starting from the architecture of the existing vision-aided inertial navigation system, this paper more focuses on contributing to the development of red boxes in Figure 1.

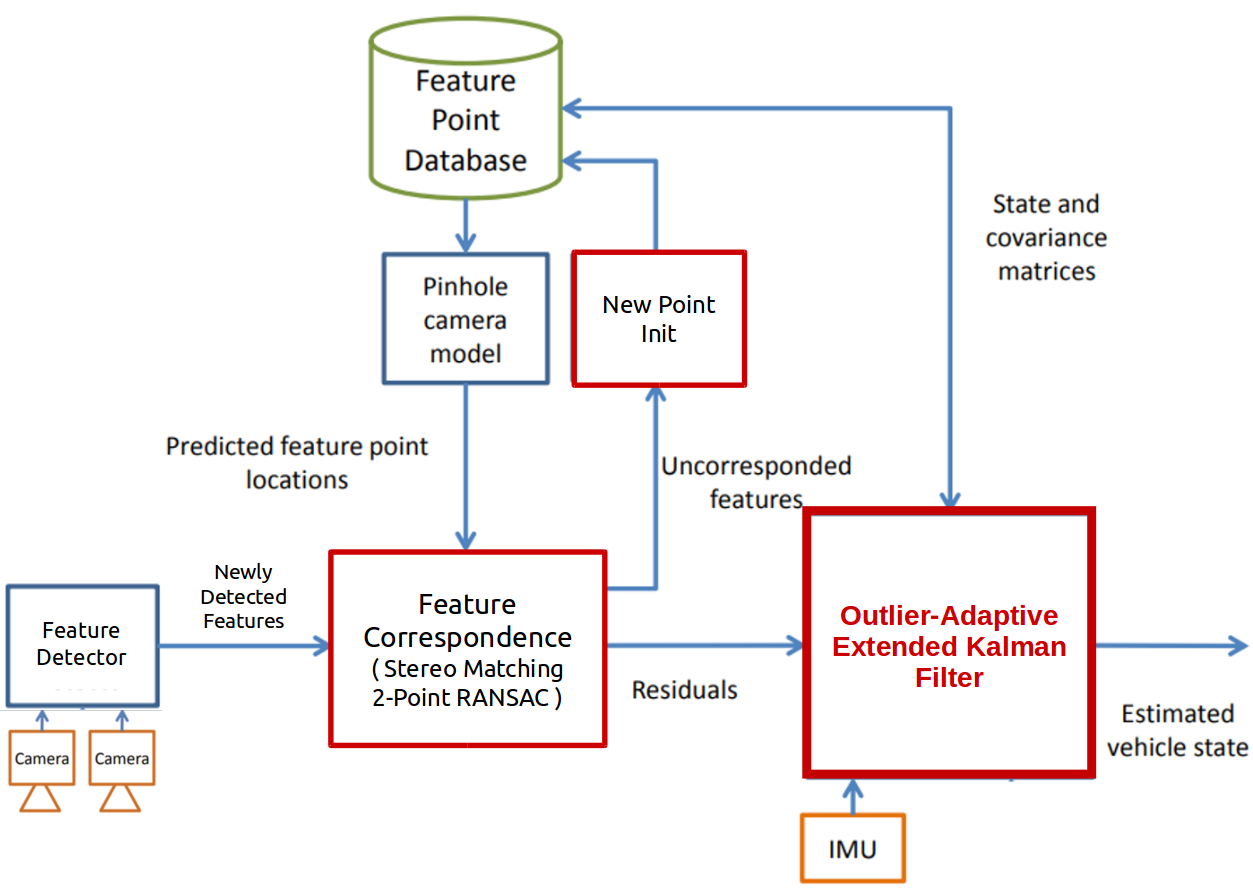
Figure 1. A block diagram of the vision-aided inertial navigation system employing the outlier-adaptive filtering.

A block diagram of the vision-aided inertial navigation system employing the

outlier-adaptive filtering.

2. Outlier Rejection in Image Processing Front-End

Our outlier rejection in image processing front-end is composed of three steps, shown in Figure 2. We assume that features from previous camera 1 and camera 2 images are outlier-rejected points, where camera 1 and camera 2 are left and right camera frames of a stereo camera, respectively. The three steps form a closed loop of previous and current frames of left and right cameras. The first step is the stereo matching of tracked features on the current camera 1 image to camera 2 image. The next steps are applying 2-point RANSAC between previous and current images of the left camera and another 2-point RANSAC between previous and current images of the right camera. For steps 2 and 3, stereo-matched features are directly used in each RANSAC.

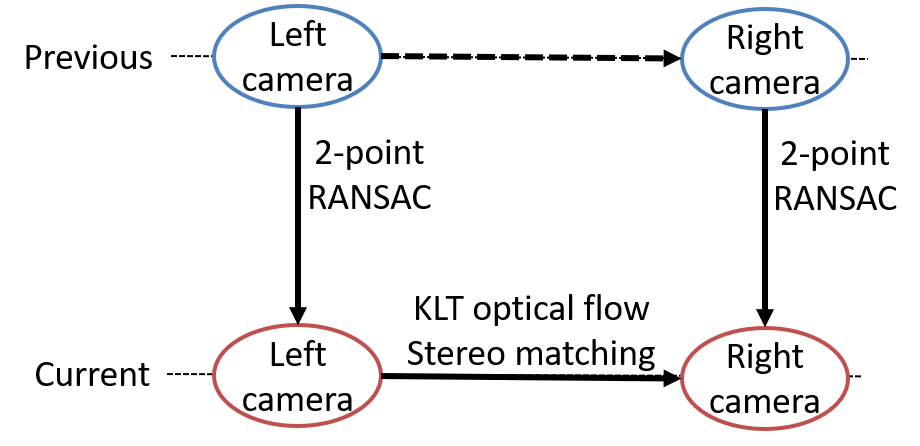
Figure 2. Close loop steps of outlier rejection in image processing front-end.

Close loop steps of outlier rejection in image processing front-end.

3. Outlier Adaptation in Filtering Back-End

Even though image processing front-end removes outliers by tracking, stereo matching, and 2-point RANSAC, some outlier features still survive and enter the filter as inputs. This section explains the outlier rejection procedure in filtering back-end.

Summarized Algorithm

This section summarizes and describes the implementation of the proposed method. Figure 3 illustrates a flow chart of the overall process of the outlier-adaptive filtering approach for V-INS. For the robust outlier-adaptive filter presented in this paper, the blue boxes in Figure 3 are extended from the figure in [

25].

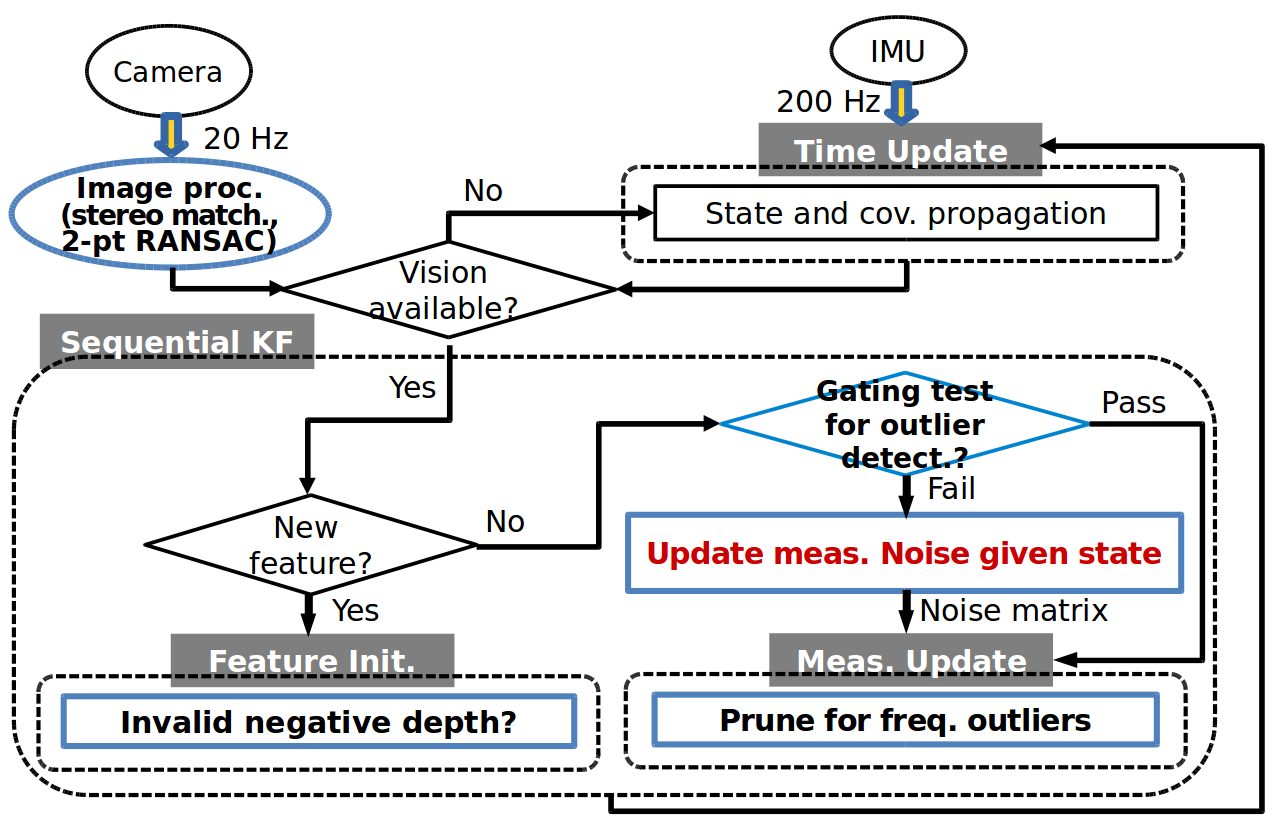
Figure 3. A flow chart of the overall process of the outlier-adaptive filtering.

A flow chart of the overall process of the outlier-adaptive filtering.

4. Discussion

This entry has presented practical outlier-adaptive filtering for a vision-aided inertial navigation systems (V-INS) and evaluated its performance with flight datasets testing. In other words, this study develops a robust and adaptive state estimation framework for V-INS under frequent outliers occurrence. In the image processing front-end of the framework, we propose the improved utilization of outlier removal techniques. In filtering back-end, for estimating the states of V-INS with measurement outliers, we implement a novel approach of the outlier-robust extended Kalman filter (EKF) to V-INS, for which we derive iterative update steps for computing the precision noise matrices of vision outliers when the Mahalanobis gating test detects remaining outliers.

This paper has presented practical outlier-adaptive filtering for a vision-aided inertial navigation systems (V-INS) and evaluated its performance with flight datasets testing. In other words, this study develops a robust and adaptive state estimation framework for V-INS under frequent outliers occurrence. In the image processing front-end of the framework, we propose the improved utilization of outlier removal techniques. In filtering back-end, for estimating the states of V-INS with measurement outliers, we implement a novel approach of the outlier-robust extended Kalman filter (EKF) to V-INS, for which we derive iterative update steps for computing the precision noise matrices of vision outliers when the Mahalanobis gating test detects remaining outliers.

To validate the accuracy of the proposed approach and compare it with other state-of-the-art V-INS algorithms, we test the performance of V-INS employing the outlier-adaptive filtering algorithm in the realistic benchmark flight datasets. In particular, to show more improvements of our method over the others’ approaches, we use the fast motion and motion blur flight datasets. Results from the flight datasets testing show that the novel navigation approach in this study improves the accuracy and reliability of state estimation in V-INS with frequent outliers. Using the outlier-adaptive filtering reduces the root mean square (RMS) error of the estimates and accelerates the robustness of the estimates, especially for the motion blur datasets.

The primary goals of future work are listed as follows. Since an inertial measurement unit (IMU) is also a sensor, it could generate outliers in V-INS. With accounting for the process outliers, the accuracy and robustness of the estimator would be improved. If we distinguish process outliers from IMU sensors with measurement outliers from vision data, the extended outlier-robust EKF [

] may be an impressive and innovate approach for this case. Furthermore, the investigation of color noise in V-INS is another possible future work. One of the required assumptions of the Kalman filter is the whiteness of measurement noise. As an illustration, during sampling and transmission in image processing, color noise that may be originated from a multiplicity of sources could degrade the quality of images [

]. The vibrational effects of camera sensors might also produce colored measurement noise [

]. That is, if the residuals of vision data are correlated with themselves at different timestamp, then colored measurement noise occurs in V-INS. Therefore, the images with color noise would be filtered for ensuring the accuracy of locating landmarks. As modeling noise without additional prior knowledge of the noise statistics is typically difficult, the machine learning techniques-based state estimator for colored noise [

62] may handle the unknown correlations in V-INS.

This entry showcases the approaches using stereo cameras but is also suitable for monocular V-INS and employable to other filter-based V-INS frameworks. We test benchmark flight datasets to validate the reliability and robustness of this study, but additional validating with other flight datasets or real-time flight tests would help to prove its more robustness. In addition, we can operate unmanned aerial vehicles (UAVs) stacked the navigation algorithms in this study and a controller-in-the-loop. The use of the controller-in-the-loop could be a more important validation criteria due to the potential for navigation-controller coupling. The research objectives and contributions presented here will remarkably advance the state-of-the-art techniques of vision-aided inertial navigation for UAVs.

] may handle the unknown correlations in V-INS.

This study showcases the approaches using stereo cameras but is also suitable for monocular V-INS and employable to other filter-based V-INS frameworks. We test benchmark flight datasets to validate the reliability and robustness of this study, but additional validating with other flight datasets or real-time flight tests would help to prove its more robustness. In addition, we can operate unmanned aerial vehicles (UAVs) stacked the navigation algorithms in this study and a controller-in-the-loop. The use of the controller-in-the-loop could be a more important validation criteria due to the potential for navigation-controller coupling. The research objectives and contributions presented here will remarkably advance the state-of-the-art techniques of vision-aided inertial navigation for UAVs.

References

Kyuman Lee; Eric N. Johnson; Robust state estimation and online outlier detection using eccentricity analysis. 2017 IEEE Conference on Control Technology and Applications (CCTA) 2017, ., 1350-1355, 10.1109/ccta.2017.8062646.
Gabriel Agamennoni; Juan I. Nieto; Eduardo Nebot; An outlier-robust Kalman filter. 2011 IEEE International Conference on Robotics and Automation 2011, ., 1551-1558, 10.1109/icra.2011.5979605.
Bernd Kitt; Andreas Geiger; Henning Lategahn; Visual odometry based on stereo image sequences with RANSAC-based outlier rejection scheme. 2010 IEEE Intelligent Vehicles Symposium 2010, ., 486-492, 10.1109/ivs.2010.5548123.
Ke Sun; Kartik Mohta; Bernd Pfrommer; Michael Watterson; Sikang Liu; Yash Mulgaonkar; Camillo J. Taylor; Vijay Kumar; Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight. IEEE Robotics and Automation Letters 2018, 3, 965-972, 10.1109/lra.2018.2793349.