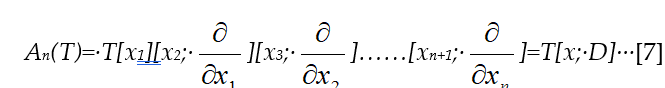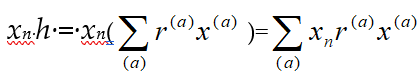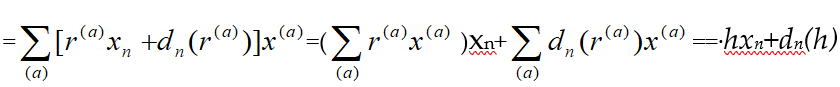1. Introduction

The history of Science shows that progress in mathematics is achieved in two ways. The first way is connected to the effort of applying mathematics to solve real world problems, or problems of the everyday life. Frequently, however, the already known mathematical theories are proved to be not suitable or enough to solve the corresponding problems. In such cases the scientists are forced to develop new mathematics in order to overcome the existing difficulties. Characteristic examples of this case are the recently developed theories of Fuzzy Sets ^{[1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17]}[1]  and of Chaotic Dynamics and Fractals ^[2][3], which have found important applications in many sectors of the human activity.

The second way of progress in mathematics concerns pure mathematical research, i.e. the process of “doing mathematics for mathematics".  The amazing thing in this case, however, is that usually theories developed through pure mathematical research, find, sometimes many years after their initial appearance, successful and often unsuspected applications to real situations. As an example, the non-Euclidean Geometries, developed on a purely theoretical basis by Lobachevsky, Riemann and others during the 19^th century (e.g. ^[4], Section 3) helped later Einstein to prove his famous Relativity Theory, which has replaced the Newton’s classical theory of gravity for the existing great masses and distances in the Universe (outside the Earth) ^[5]. Another example is the Knot theory, initiated from a false model for the description of the atom’s theory, which however proved later to be the key for understanding the basic mechanisms of the DNA!

Examples analogous to the previous two can be found in abundance in the history of mathematics. The Nobel Prize winner E.P. Winger has characterized this phenomenon as “the unreasonable effectiveness of Mathematics in the Natural Sciences”, a characterization which is widely known as the Winger’s enigma ^[4]. This phenomenon rises a question which has occupied for centuries, and still occupies, the interest of philosophers, mathematicians and other scientists: Is actually Mathematics INVENTED or DISCOVERED by humans? The great ancient Greek philosopher Plato introduced the idea of the existence of an abstract “Universe of Mathematics”, parts of which are eventually discovered by humans. His theory, usually referred as Platonism, despite the blows that has received during the centuries by the development of several mathematical theories and the opposite views of many other philosophers, social thinkers and scientists, has still many supporters in our times ^[4].

The present study focuses on Skew Polynomial Rings (SPRs), a topic of abstract Algebra which can be considered also as an example of the Winger’s enigma. SPR have been firstly introduced by Ore ^[6] in 1933 over a division ring R and that is why they are also called Ore extensions. Those rings were initially used as counter examples, but eventually a great attention was given to them and many papers were written, especially during the 1970’s and 1980’s, since it was realized that they have an important theoretical interest.

The researchers’ interest about SPRs has been renewed recently, because they have found two important applications. The first application is related to the use of quantum groups as a tool of Theoretical Physics. It is recalled that a quantum groups is a Hopf algebra having in addition a structure analogous to that of a Lee group ^[7]. It has been observed that most of these algebras can be expressed in the form of a SPR.

The second application concerns the use of SPRs in coding theory. More explicitly, Jatengaokar ^[8] studied in detail the structure of monomorphism skewed polynomial rings over semi-simple rings showing that they are direct sums of matrix rings. Jatengaokar’s structure theorem for SPRs has been recently used in coding theory to analyze the structure of certain convolutional codes. For the same purpose, Jatengaokar’s results hav ^[9]. 

The rest of the present article is organized as follows: Section 2 includes the definitions and some examples of SPRs and of Iterated SPRs (ISPRs), i.e. SPRs in finitely many variables. In Section 3 a special class of ISPRs is introduced over a ring R with respect to a finite set of pairwise commuting derivations of R, some important properties of the ISPRs of this class are presented, and examples are given. The paper closes with the final conclusions, which are stated in Section 4.   

2. Skew Polynomial Rings

Let R be a ring with identity. In order to define a SPR over R, we extend the notion of a derivation of R as follows:

Definition 2.1: Let f and g be endomorphisms of R and let d: R R be a map satisfying, for all a, b in R, the properties:

• d(a+b)=d(a)+d(b)
• d(ab)= g(a)d(b)+d(a)f(b).

Then d is called a (f,g)-derivation of R.

If both f and g are identity maps, then d becomes a classical derivation of R. Also, if only g is the identity map, then d is called an f-derivation of R or a skew derivation of R defined with respect to f.

Let now f be a monomorphism of R and let d be an f-derivation of R. Then we define a SPR over R as follows:

Definition 2.2: Consider the set S of all polynomials in one variable, say x, over R. Define addition in S in the usual way and multiplication by the distributive law with respect to addition and by the by the rule

xr=f(r)x+d(r)      (1).

Then it is straightforward to check that S becomes a ring, called a skew (or twisted) polynomial ring over R and denoted by R[x; f, d].

In Definition 2.2, f has been considered to be a monomorphism, and not a simple endomorphism of R, just to block the case for x to be a zero divisor of S. In fact, if there were r₁ r₂ in R such that f(r₁)=f(r₂), then by equation (1) we should have

x(r₁-r₂)=xr₁-xr₂=f(r₁)x+d(r₁)-[f(r₂)x+d(r₂)}=d(r₁-r₂).

Therefore, if r₁-r₂ is in the kernel of d, we should have x(r₁-r₂)=0.

If f is the identity map, then S is denoted by R[x; d] and is called a SPR of derivation type over R. Then equation (1) gives, for all r in R, that

xr = rx + d(r)        (2).

Using equation (2) and applying induction on n one finds, for all r in R and all positive integers n, that

(3)

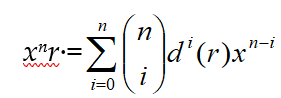
Also, if d is the zero derivation of R, then the SPR S is denoted by R[x; f], where multiplication is defined, for all r in R, by the distributive law and the equation

xr = f(r)x     (5)

Applying induction on n one finds from equation (5) that, for all r in R and all positive integers n, is

xⁿr = fⁿ(r)xⁿ      (6)

Example 2.3: Let T[x₁] be a polynomial ring over a ring T, then the SPR T[x₁][x₂; ] over T[x₁] is called the first Weyl algebra over T and is denoted by A₁(T). It becomes evident that the elements of A₁(T) are polynomials in two variables x₁ and x₂ over T and multiplication, for all t in T, is defined by

x₁t=tx₁, x₂t=tx₂+ = tx₂, x₂x₁=x₁x₂+ =x₁x₂+1       (4)

Next, following ^[10] one can define an ISPR over R as follows:

Definition 2.4: Let S₁=R[x₁; f₁, d₁] be a SPR over the ring R, where f₁ is a monomorphism and d₁ is a f₁-derivation of R. Then, if f₂ is a monomorphism and d₂ is a f₂-derivation of S₁, the SPR S₂=S₁[x₂; f₂, d₂] is called an ISPR over R and is denoted by S₂=R[x₁; f₁, d₁][x₂; f₂, d₂].

Keep the same notation and set S₀=R. Consider the finite sets H={f₁,f₂,…,f_n}, where f_i is a monomorphism of S_i-1 , and D={d₁,d₂,…d_n}, where d_i is a f_i-derivation of S_i-1, for i=1,0,…,n. Then by induction one defines the ISPR S_n=R[x₁; f₁, d₁][x₂; f₂, d₂]….[x_n; f_n, d_n] over R . In order to simplify our notation we shall denote this ring by S_n=R[x; H, D].

When all the elements of H are identity maps, then S_n is denoted by R[x; D] and is called an ISPR of derivation type over R. Also, when all the elements of D are zero derivations, then one obtains the ISPR S_n=R[x; H], which is defined with respect to the set H of endomorphisms of R.

Examples 2.5: 

(i) The first Weyl algebra A₁(T) over a ring T (Example 2.3) is an ISPR of derivation type in two variables over T of the form T[x₁; d][x₂, ], where d denotes the zero derivation of T. In this case T[x₁; d] is the ordinary polynomial ring T[x₁].

(ii) Set R= A₁(T). Then the first Weyl algebra A₁(R) over R is called the second Weyl algebra over T and is denoted by A₂(T). Obviously we have that

A₂(T)= A₁[A₁(T)]=T[x₁][x₂; ][x₃; ].

(iii) Consider the set of all polynomials in n+1 variables, say x₁,x₂,…, x_n,x_n+1, over a ring T. Then the n-th Weyl algebra A_n(T) over T is defined by induction as A_n(T)=A₁[A_n-1(T)]. Denote by d the zero derivation of T and set 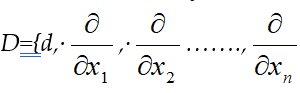 . Then, one can write

3. On a Special Class of Iterated Skew Polynomial Rings of Derivation Type

In this section, given a finite set D of pairwise commuting derivations of R, we shall construct an ISPR R[x; D] of derivation type over R. For this, we need the following lemma:

Lemma 3.1: Let R be a ring, let d be a derivation of R, let S=R[x; d] be the SPR over R defined with respect to d, and let d₁ be another derivation of R. Then d₁ can be extended to a derivation of S by d₁(x)=0, if, and only if,  d₁ commutes with d.

Proof: Assume first that d₁ can be extended to a derivation of S by d₁(x)=0. Then, for all r in R, we have that d₁(xr)=d₁(x)r+xd₁(r)= xd₁(r)  (8)

Then, by equation (2)  we have that  d₁(xr)=d₁[rx+d(r)]=d₁(rx)+ d₁[d(r)]

= d₁(r)x+ d₁(x)+ d₁[d(r)] =d₁(r)x+d₁[d(r)]   and xd₁(r)=d₁(r)x+d[d₁(r)]. Therefore (8) gives that d₁[d(r)]= d[d₁(r)] for all r in R, which shows that  d₁od = dod₁.

Conversely assume that d₁od= =dod₁. Then, if d₁ can be extended to a derivation of S, we must have, for all r in R, that d₁(xr)= d₁(x)r+ xd₁(r) (9)

But, as before, we find that d₁(xr)=d₁(r)x+ d₁(x)+ d₁[d(r)] and xd₁(r)=d₁(r)x+d[d₁(r)]. Therefore. (9) gives that d₁(r)x+ d₁(x)+ d₁[d(r)]= d₁(x)r+ d₁(r)x+d[d₁(r)] or d₁(x)= d₁(x)r, which is true for d₁(x)=0.

We are ready now to prove the following theorem:

Theorem 3.2: Let R be a ring, and let D={d₁,d₂,….,d_n} be a finite set of derivations of R. Set S₀=R and denote by S_i the set of all polynomials in variables, say x₁, x₂,…., x_i, with coefficients in R, for i=0,1,2,….,n. Define in S_n addition in the usual way and multiplication by the distributive law with respect to addition and by the rules

x_ir=rx_i+d_i(r) for all r in R, x_ix_j=x_jx_i  for i,j=1,2,….n  (10).

Then S_i is a SPR of derivation type) over S_i-1, for all i=1,2,…n, if, and only if, d_iod_j=d_jod_i, for all i, j=1,2,….n.

Proof: Assume first that the elements of D commute to each other. Obviously S₁=R[x₁; d₁] is a SPR over R. We apply induction on n. For this, assume that S_i is a skew polynomial ring over S_i-1 for each i . By Lemma 3.1 d_n is extended to a derivation of S₁ by d_n(x₁)=0. But, by our inductive hypothesis, S₂=S₁[x₂, d₂] is a skew polynomial ring over S₁. Therefore, by Lemma 3.1 d_n, being a derivation of S₁, can be extended to a derivation of S₂ by d_n(x₂)=0 and so on. Keep going in the same way one finds after a finite number of steps that d_n can be extended to a derivation of S_n-1 by d_n(x_i)=0, i=1,2,…,n-1.

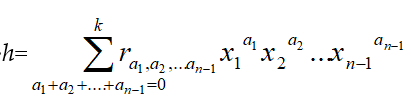
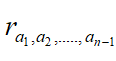
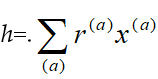
Let now be an element of S_n-1, with  in R. For reasons of brevity we write . Then

Thus S_n=S_n-1[x_n; d_n] is a SPR over S_n-1.

Conversely, assume that S_i is a SPR over S_i-1, for all i=1,2,.,n. Then, since S_n=S_n-1[x_n,d_n] is a SPR over S_n-1 and x_i belongs to S_n-1 for each i, 1 <n, we have that x_nx_i=x_ix_n+d_n(x_i). Therefore by the second of rules (10), we get that d_n(x_i)=0.

Further, given r in R we have that x_ir=rx_i+d_i(r). Therefore d_n(x_ir)=d_n(rx_i)+d_n[d_i(r)], or x_id_n(r)=d_n(r)x_i+d_n[d_i(r)]. But x_id_n(r)= d_n(r) x_i+d_i[d_n(r)] and the last two equalities imply that d_nod_i=d_iod_n. In the same way and for each j=1,2,…,n,  one can show that d_jod_i=d_iod_j, for all i, 1 i<j and this completes the proof.

Theorem 2.2 shows that, if the derivations of D commute to each other, then S_n=R[x; D], with addition defined in the usual way and multiplication by the rules (10) and the distributive law, is an ISPR of derivation type over R.

In a more general context, one can define an ISPR over R of the form R[x; H, D] with H a finite set of monomorphisms of R and D a finite set of skew derivations of R defined with respect to the monomorphisms of H, provided that all these maps commute pairwise to each other (^[11], Theorem 2.4).

The following example illustrates Theorem 3.2:

Example 3.3: Let R=T[y₁,y₂,….,y_n] be a polynomial ring over a ring T.

Set D={ , ,…., }. Since the elements of R are polynomials with coefficients in T, their partial derivatives are continuous functions. Therefore, by the Young’s classical theorem of differential calculus, the derivations of D commute to each other.

Consider the set S_n of all polynomials in n variables, say x₁, x₂,…., x_n, with coefficients in R and define in  S_n addition in the usual way and multiplication by the rules

hx_i=x_ih+  for all h in R and x_ix_j=x_jx_i, i, j=1,…,n.

Then, by Theorem 3.2, S_n=R[x; D] is an ISPR of derivation type over the polynomial ring R. It is easy to check that y_ix_i=x_iy_i+1, while y_ix_j=x_jy_i for i ,  i, j=1,2,…,n. 

Remarks 3.4: 

• In order to be in the ISPR of Theorem 3.2  it is necessary to have

d_i o d = d o d _I, for all i, j=1,2,…,n.  In fact, given r in R, we have

r = x ] = (x_ir)x_j + x_id_j(r) = rx_ix_j + d_i(r)x_j + d_j(r)x_i  + (d_iod_j)(r). In the same way one finds that x r = rx_jxi + d_j(r)x_i + d_i(r)xj + (d_jod_i)(r). The result follows by equating the right hand sides of those two equations.

2. ii) If there exist, however, x’s in S_n not commuting to each other, this does not mean that the same must happen with the derivations of D. An example illustrating this situation is the n-th Weyl algebra A_n(T) over a ring T, n  (see example 2.5, iii).  In fact, the elements of A_n(T) are polynomials over T and therefore, as we have shown above, the derivations of D commute to each other, whereas the x’s don’t commute (Example 2.3).

iii)  SPRs in finitely many variables over a ring R, not necessarily commuting to each other, with respect to a finite set of derivations of R have been firstly introduced by Kishimoto ^[12]. In those SPRs, which need not be ISPRs over R, multiplication is defined by the first (only) of rules (10) and the distributive law.

We shall close this article by mentioning some important properties of the special class of ISPRs defined in this Section, which have been proved in earlier works of the present author. For this, it is necessary to recall the following definitions:

Definition 3.5: A derivation d of a ring R is called an inner derivation induced by an element s of R, if d(r)=sr-rs, for all r in R. A derivation of R which is not inner is called an outer derivation.

Note also that an outer derivation of R is possible to be extendable to an inner derivation of a SPR of derivation type over R. For example, d=  is an outer derivation of the polynomial ring R=T[x₁] over a ring T, because x₁ is a central element of R and d(x₁)=1 . But d is extended to an inner derivation of A₁(T)=R[x₂,d] induced by x₂, because, by the definition of multiplication in A₁(T), we have that x₂f=fx₂+d(f), or d(f)=x₂f-fx₂, for all f in R.

Definition 3.6: Let R be a ring and let D be a set of derivations of R. Then an ideal I of R is called a D-ideal, if d(I) I  for all derivations d in D , and R is called a D-simple ring if it has no non trivial D-ideals.

Every D-simple ring R contains the field F= C(R) ker d], where C(R) denotes the center of R, therefore R is either of characteristic zero or of a prime number p. Non commutative D-simple rings exist in abundance, e.g. every simple ring R is D-simple for any set D of derivations of R. Characteristic examples of commutative D-simple rings can be found in ^[13].

Definition 3.7: Let D be a set of derivations of a ring R. Then, a D- ideal I of R is called D-prime ideal, if, given any two D-ideals A, B of R such that AB I, is either A , or B . Also, I is called D-semiprime ideal, if for all D-ideals A of R and any positive integer k such that A^k , is A .

Remarks 3.8:

(i) Let R be a ring of characteristic zero and let D={d₁,……, d_n} be a finite set of derivations of R commuting to each other. Set S₀=R and assume that R is a D-simple ring and that d_i is an outer derivation of S_i-1, for i=1,2,…,n. Then S_n=R[x; D] is a simple ring (^[14], Theorem 3.4).

Conversely, if S_n=R[x; D] is a simple ring, then no element of D is an inner derivation of R induced by an element of , where Kerd is the kernel of d, and R is a D-simple ring ([14], Theorem 3.3).

Analogous results, with a little bit more complicated statement, hold if R is of prime characteristic (^[15], Theorems 2.3 and 2.4).

As an immediate consequence of the previous results, if R is a commutative ring, then S_n=R[x; D] is a simple ring, if, and only if, R is a D-simple ring.

 (ii) Let R, D and S_n be as in the previous remark. Then, if P is a prime ideal of S_n, P R is a D-prime ideal of R ([16], Theorem 2.2]. Conversely, if I is a D-prime ideal of R, then IS_n is a prime ideal of S_n (^[16], Theorem 2.6). Analogous relations hold among the semiprime ideals of S_n and the D-semiprime ideals of R ^[17].

4. Conclusion

The study of SPRs used to be of great theoretical importance for the abstract Algebra some decades ago, but the recent renewal of interest about them is due to the fact that they have found practical applications too.  In this work a special class of ISPRs over a ring R with respect to a finite set D of pairwise commuting derivations of R was constructed. The simplicity of those ISPRs is connected to the D-simplicity of R and their prime ideals correspond to D-prime ideals of R. The attempt to obtain further properties of those ISPRs with respect to corresponding properties of R could be a good hint for future research on the subject.