Your browser does not fully support modern features. Please upgrade for a smoother experience.
From Airy’s Equation to the Non-Dissipative Lorenz Model: Turning Points, Quantum Tunneling, and Solitary Waves: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Abigail Zou and Version 1 by Bo-Wen Shen.

This report bridges fundamental ideas from introductory calculus to advanced concepts in quantum mechanics and nonlinear dynamics. Beginning with the behavior of second derivatives in oscillatory and exponential functions, it introduces the Airy equation and the WKB approximation as mathematical tools for describing wave propagation and quantum tunneling near turning points—locations where transitions between oscillatory and exponential components occur. The analysis then extends to the non-dissipative Lorenz model, whose double-well potential and solitary-wave (sech-type) solutions reveal a deep mathematical connection with the nonlinear Schrödinger equation. Together, these examples highlight the universality of second-order differential equations in describing turning-point dynamics, encompassing physical phenomena ranging from quantum tunneling to coherent solitary-wave structures in fluid and atmospheric systems.

  • quantum tunneling
  • turning points
  • quantum mechanics
  • nonlinear dynamics
  • solitary waves
  • propagating waves
  • evanescent waves
  • the Airy equation
  • the Schrödinger equation
  • the non-dissipative Lorenz model
In 2025, the Nobel Prize in Physics was awarded for pioneering research related to the phenomenon of quantum tunneling [1,2,3,4,5,6,7,8][1][2][3][4][5][6][7][8] (see Figure 1). Quantum tunneling describes how particles can traverse potential barriers that would be classically forbidden—a process central to nuclear fusion in stars [9[9][10],10], semiconductor devices [11], and scanning tunneling microscopy [12,13][12][13]. This remarkable discovery not only deepened our understanding of quantum mechanics but also inspired new perspectives on wave propagation and energy transfer across different physical systems. Figure 1 highlights the scientific importance of this concept.
Encyclopedia 05 00208 g001
Figure 1. Quantum tunneling. The illustration is adapted from the 2025 Nobel Prize in Physics press material, awarded for pioneering work on quantum tunneling, and is reproduced with permission. Credit: © Johan Jarnestad/The Royal Swedish Academy of Sciences [7].
Originally derived from the Schrödinger equation, the phenomenon of tunneling can be described mathematically through the Airy equation [14,15][14][15] and the WKB (Wentzel–Kramers–Brillouin) approximation ([14,16,17,18,19,20,21,22,23,24][14][16][17][18][19][20][21][22][23][24]). These methods reveal how an oscillatory (propagating) solution transitions smoothly into an exponentially decaying (evanescent) solution near a turning point. The Airy equation provides a local model valid near the turning point, while the WKB method offers an asymptotic description of the same wave behavior away from it.
Beyond quantum mechanics, the same mathematical structures emerge in nonlinear systems. The nonlinear Schrödinger (NLS) equation ([25]) and the non-dissipative Lorenz model ([26]) share strikingly similar amplitude equations that govern solitary waves and homoclinic orbits. This correspondence demonstrates the beauty of mathematical universality: the same second-order nonlinear differential forms that describe quantum tunneling also govern coherent wave structures in fluid dynamics and atmospheric models.
This report, therefore, explores how fundamental second-order differential equations connect seemingly different phenomena—the propagation of waves, quantum tunneling, and nonlinear solitary waves. Beginning from elementary calculus concepts, we trace a logical path from simple oscillations to complex nonlinear dynamics represented by the non-dissipative Lorenz model. The goals are twofold: (1) to help students who have completed Calculus I and II visualize the mathematical meaning of turning points and transitions between oscillatory and exponential behaviors, and (2) to show how similar mathematical structures appear across quantum mechanics, wave theory, and nonlinear dynamics.
This report is organized as follows. Section 2 reviews the properties of second derivatives of the sine, cosine, and exponential functions to help first-year college students who have completed Calculus I and II understand the concepts of propagating and evanescent modes. Building on these introductory ideas, Section 3 demonstrates how a local analysis of the linear Schrödinger equation leads to the Airy equation, which contains a turning point where a transition between oscillatory and exponential components occurs. The corresponding Ai

and Bi solutions of the Airy equation are presented, followed by an introduction to the WKB approximation. Section 4 discusses the non-dissipative Lorenz model, identifies two turning points in its structure, and establishes its relationship with the amplitude equation of the nonlinear Schrödinger equation (NLS). A summary is provided at the end. Appendix A and Appendix B offer additional details on the analysis of phase and amplitude in the nonlinear and linear Schrödinger equations, respectively. Appendix C offers a concise overview of the non-dissipative Lorenz model. Appendix D discusses effective turning points of the non-dissipative Lorenz model.

References

  1. Caldeira, A.O.; Leggett, A.J. Influence of Dissipation on Quantum Tunneling in Macroscopic Systems. Phys. Rev. Lett. 1981, 46, 211–214.
  2. Clarke, J.; Cleland, A.N.; Devoret, M.H.; Esteve, D.; Martinis, J.M. Quantum Mechanics of a Macroscopic Variable: The Phase Difference of a Josephson Junction. Science 1988, 239, 992–997.
  3. Devoret, M.H.; Martinis, J.M.; Clarke, J. Measurement of Macroscopic Quantum Tunneling out of a Zero-Voltage State of a Current-Biased Josephson Junction. Phys. Rev. Lett. 1985, 55, 1908–1911.
  4. Gunn, J.B. The 1973 Nobel Prize for physics. Proc. IEEE 1974, 62, 823–824.
  5. Martinis, J.M.; Devoret, M.H.; Clarke, J. Energy-Level Quantization in the Zero-Voltage State of a Current-Biased Josephson Junction. Phys. Rev. Lett. 1985, 55, 1543–1546.
  6. The Royal Swedish Academy of Sciences. The Nobel Prize in Physics 2025—Popular Information. Available online: https://www.nobelprize.org/prizes/physics/2025/popular-information/ (accessed on 26 November 2025).
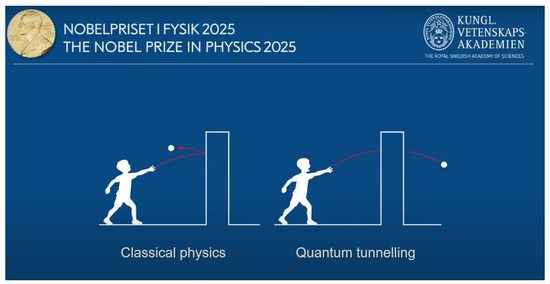
  7. The Royal Swedish Academy of Sciences. The Nobel Prize in Physics 2025—Popular Information. Available online: https://www.nobelprize.org/uploads/2025/10/press-physicsprize2025-figure2.jpg (accessed on 26 November 2025).
  8. Voss, R.F.; Webb, R.A. Macroscopic Quantum Tunneling in 1-µm Nb Josephson Junctions. Phys. Rev. Lett. 1981, 47, 265–268.
  9. Bethe, H.A. Energy Production in Stars. Phys. Rev. 1939, 55, 103–147.
  10. Gamow, G. Zur Quantentheorie des Atomkernes. Z. Für Phys. 1928, 51, 204–212.
  11. Nobel Foundation. The Nobel Prize in Physics 1973. Available online: https://www.nobelprize.org/prizes/physics/1973/summary (accessed on 26 November 2025).
  12. Binnig, G.; Rohrer, H. Scanning Tunneling Microscopy—From Birth to Adolescence. 1987. Available online: https://www.nobelprize.org/uploads/2018/06/binnig-lecture.pdf (accessed on 26 November 2025).
  13. The Nobel Prize in Physics 1986. 1986. Available online: https://www.nobelprize.org/prizes/physics/1986/summary (accessed on 26 November 2025).
  14. Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory; Springer: New York, NY, USA, 1999.
  15. Dunster, T.M. Simplified Airy function asymptotic expansions for reverse generalised Bessel polynomials. arXiv 2025, arXiv:2506.20934.
  16. Brillouin, L. La mécanique ondulatoire de Schrödinger: Une méthode générale de resolution par approximations successives. Comptes Rendus L’AcadéMie Sci. 1926, 183, 24–26.
  17. Gill, A.E. Atmosphere–Ocean Dynamics, 1st ed.; International Geophysics Series; Academic Press: Cambridge, MA, USA, 1982; Volume 30.
  18. Green, G. On the motion of waves in a variable canal of small depth and width. Trans. Camb. Philos. Soc. 1837, 6, 457–462.
  19. Kramers, H.A. Wellenmechanik und halbzahlige Quantisierung. Z. Für Phys. 1926, 39, 828–840.
  20. Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory, 3rd ed.; Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1977; Volume 3.
  21. Liouville, J. Sur le développement des fonctions et séries. J. Mathématiques Pures Appliquées 1837, 1, 16–35.
  22. Mathews, J.; Walker, R.L. Mathematical Methods of Physics, 2nd ed.; Addison–Wesley: Boston, MA, USA, 1970.
  23. Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2017.
  24. Wentzel, G. Eine Verallgemeinerung der Quantenbedingungen für die Zwecke der Wellenmechanik. Z. Für Phys. 1926, 38, 518–529.
  25. Haberman, R. Applied Partial Differential Equations with Fourier Series and Boundary Value Problems, 5th ed.; Pearson Education, Inc.: London, UK, 2013; p. 756.
  26. Shen, B.-W. Homoclinic Orbits and Solitary Waves within the Non-dissipative Lorenz Model and KdV Equation. Int. J. Bifurc. Chaos 2020, 30, 2050257.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Academic Video Service
Feedback