1. Special Notes on Obidi's Gravity from Newton and Einstein in the Theory of Entropicity(ToE)

Obidi's Gravity from Newton, Einstein, Verlinde, Padmanabhan, and Others

The Theory of Entropicity (ToE), ^[1][2][3][4] as formulated in this treatise, offers a profound departure from prior approaches to gravity, including those of Newton, Einstein, Verlinde, Padmanabhan, and other entropic and geometric theorists. This section systematically outlines the comparative landscape, highlighting ToE's originality, mathematical innovations, and foundational shifts ^[5][6][7].

Setup of the Derivation of Newtonian Gravity from Entropy Gradient

Consider a static, spherically symmetric mass \(M\) localized at the origin. To leading order, the entropy field \(S(x)\) obeys a Poisson-like equation (see §7.4):

\[

\nabla^2 S(x) \;=\; -\,\eta\,\rho_M(x)

\quad\text{with}\quad

\rho_M(x) = M\,\delta^3(x)\,,

\]

Outside the mass distribution we have \(\nabla^2 S = 0\). Solving Laplace’s equation in spherical symmetry gives

where \(S_\infty\) is the asymptotic (far-field) value of the entropy.

Entropic Force

A test particle of mass \(m\) moves so as to increase the total entropy. Its equation of motion follows from the entropic variational principle (see §5.2):

\[

\mathbf{F}_{\mathrm{entropy}}

= -\,m\,\nabla \Phi_S(r)

\,,\qquad

\Phi_S(r) \equiv S(r).

\]

Substitute the radial solution for \(S(r)\):

\[

\frac{\eta}{4\pi} \;=\; G

\]

thus reproduces Newton’s law of universal gravitation:

\[

\mathbf{F}_{\mathrm{entropy}}

= -\,\frac{G\,M\,m}{r^2}\,\hat{\mathbf{r}}\,,

\]

an attractive \(1/r^2\) force arising from the gradient of the entropy field in the Theory of Entropicity (ToE).

ToE Reinterprets Entropy as a Source of Constraint Curvature

The Theory of Entropicity (ToE) breaks with tradition by proposing that:

• All observed curvatures in spacetime and trajectories are not due to spacetime geometry itself, but arise from entropy gradients and their associated field constraints.
• Thus, the entropy field directly modifies the effective force, not only in a Newtonian sense but in a fully relativistic, irreversible, and time-asymmetric manner.
• From this perspective, ToE extends the classical Binet equation with an entropic source term that naturally accounts for observed relativistic corrections.

This extension is therefore entirely novel:

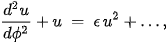
where the additional terms arise from entropic field constraints (e.g., via ) and are derived from the Master Entropic Equation (MEE) or the entropy-constrained geodesic equation of the Theory of Entropicity.

In doing so, ToE redefines the source of curvature from a purely geometrical model to a field-theoretic model governed by entropy, rendering the Binet equation once again a valid and powerful tool—now enriched by entropic effects.

We begin by contrasting the ToE with Erik Verlinde's entropic gravity, arguably the most well-known recent attempt to link gravitation to entropy:

2.

Comparison with Verlinde's Entropic Gravity

 

 

 

Comparison of Verlinde's Entropic Gravity and the Theory of Entropicity (ToE)

Aspect	Verlinde's Entropic Gravity	Theory of Entropicity (ToE)
Nature of Entropy	Emergent and statistical; linked to coarse-graining and information loss on holographic screens	Fundamental and field-like; a causal, dynamic entity that propagates as a physical field
Origin of Gravity
Gravity Source	Curved spacetime geometry	Emerges from entropy gradients ; derived from the Obidi Action
Entropic field gradients	Role of Holography	Central to formulation via equipartition and boundary information	Not essential; entropy is local and volumetric
Emergent from information change on holographic surfaces	Mathematical Formulation	Thermodynamic analogies (e.g., ); lacks field equations	Derived from a full action principle; includes the Master Entropic Equation (MEE) and entropy-modified Binet equation
Quantization	No formal quantum formulation	Introduces the entropion, the quantum of the entropy field
Correction Terms	Geodesic deviation in curved space	Constraint terms from entropy flow
Field Equation	Einstein Field Equation	Master Entropic Equation (MEE)
Particle Path	Geodesic	Entropic constrained least-action path
Binet Usage	Not applicable	Emergent from entropy potential	Temporal Asymmetry	Time-symmetric	Irreversibility built in via the No-Rush Theorem and Entropic CPT violation
Equation Structure	Analogical use of thermodynamic relations	First-principles derivations from entropy-based variational dynamics
Scope	Gravitational reinterpretation	Unification of gravity, quantum mechanics, thermodynamics, and information theory
Experimental Predictions	Limited; mostly conceptual	Predicts 232 attosecond entanglement delay, entropy lensing, entropion spectra, time-asymmetric collapse, and more

Einstein's Gravity in General Relativity and Obidi's Gravity in the Theory of Entropicity(ToE)

 

Einstein's Gravity in General Relativity and Obidi's Gravity in the Theory of Entropicity(ToE)

Feature	General Relativity (GR)	Theory of Entropicity (ToE)

3. Unique Insights and Innovations in ToE on Gravity from the Binet-Obidi Equation

3.1.

1.

Entropy as a Real Dynamical Field

Unlike Verlinde, who treats entropy as a boundary phenomenon, ToE promotes entropy to a local scalar field with physical dynamics, satisfying wave equations and variational principles. This represents a fundamental ontological shift.

3.2.

2.

The Obidi Action and the Master Entropic Equation (MEE)

The Obidi Action introduces a new variational principle from which the MEE arises. This equation governs the entropic field's evolution and its interaction with matter and motion:

 

where is a nonlinear operator encoding entropy, curvature, and irreversibility.

3.3.

3.

The Vuli-Ndlela Integral

The Vuli-Ndlela Integral is a reformulated path integral for entropic dynamics:

 

This integral incorporates gravitational entropy , irreversible entropy , and an entropy-modified action.

3.4.

4.

Entropic Binet Equation

The classical Binet equation is resurrected and extended in ToE as the following Binet-Obidi Equation ^[1][2][3][4]Binet-Obidi Equation:^[1][2][3][4]

 

where and is derived from entropic corrections. This formulation reproduces Einsteinian results for Mercury's perihelion precession and light deflection without invoking spacetime curvature.

• The No-Rush Theorem and Entropic Time Limit (ETL)

1. The No-Rush Theorem and Entropic Time Limit (ETL)

These principles posit a finite lower bound on all physical interaction durations due to entropy propagation constraints. This leads to predictions like the finite 232 attosecond delay in entanglement formation.

• Black Hole Dynamics via Entropy Field

2. Black Hole Dynamics via Entropy Field

Black hole evaporation is reinterpreted as a loss of entropy field energy and the emission of quantized entropic particles (entropions), rather than Hawking’s pair production.

• Entanglement formation delay (232 attoseconds)
• Entropy lensing near strong fields
• Entropic collapse asymmetry in quantum measurements

• Testable Predictions

3. Testable Predictions

• Quantized black hole entropy spectra

4.

Why the Modified Binet Equation (the Binet-Obidi Equation) in ToE is Revolutionary

Traditionally, the Binet equation: is limited to Newtonian central force problems. GR bypasses it in favor of spacetime geodesics derived from the Schwarzschild metric. ToE reinvigorates the Binet equation by embedding it in an entropic variational principle, where the effective force arises from entropy gradients: Although does not appear explicitly in the final Binet-Obidi form, it is the generator of the correction term , making the entropy field the true origin of curvature and force.

5.

Summary and Final Word on Gravity from ToE's Binet-Obidi Formulation

Verlinde makes gravity emergent from entropy; Obidi’s ToE makes all physics emergent from entropy.

In ToE, entropy is no longer a passive measure of disorder or information, but a fundamentalfundamental force-field force-field shaping motion, structure, and time. Through the Obidi Action, MEE, the Vuli-Ndlela Integral, and the Entropic Binet-Obidi Equation, ToE offers a unified, causal, and testable alternative to traditional gravity and quantum theories. This redefines the conceptual foundations of physics and signals a new era in theoretical science.

References

1. Obidi, John Onimisi. Corrections to the Classical Shapiro Time Delay in General Relativity (GR) from the Entropic Force-Field Hypothesis (EFFH). Cambridge University. (11 March 2025). https://doi.org/10.33774/coe-2025-v7m6c
2. Obidi, John Onimisi. How the Generalized Entropic Expansion Equation (GEEE) Describes the Deceleration and Acceleration of the Universe in the Absence of Dark Energy. Cambridge University. (12 March 2025). https://doi.org/10.33774/coe-2025-6d843
3. Obidi, John Onimisi. The Theory of Entropicity (ToE): An Entropy-Driven Derivation of Mercury’s Perihelion Precession Beyond Einstein’s Curved Spacetime in General Relativity (GR). Cambridge University. (16 March 2025). https://doi.org/10.33774/coe-2025-g55m9
4. Obidi, John Onimisi. The Theory of Entropicity (ToE) Validates Einstein’s General Relativity (GR) Prediction for Solar Starlight Deflection via an Entropic Coupling Constant η. Cambridge University. (23 March 2025). https://doi.org/10.33774/coe-2025-1cs81
5. Obidi, John Onimisi. Einstein and Bohr Finally Reconciled on Quantum Theory: The Theory of Entropicity (ToE) as the Unifying Resolution to the Problem of Quantum Measurement and Wave Function Collapse. Cambridge University. (14 April 2025). https://doi.org/10.33774/coe-2025-vrfrx
6. Obidi, John Onimisi . "On the Discovery of New Laws of Conservation and Uncertainty, Probability and CPT-Theorem Symmetry-Breaking in the Standard Model of Particle Physics: More Revolutionary Insights from the Theory of Entropicity (ToE)". Cambridge University. (14 June 2025). https://doi.org/10.33774/coe-2025-n4n45
7. Obidi, John Onimisi. A Critical Review of the Theory of Entropicity (ToE) on Original Contributions, Conceptual Innovations, and Pathways towards Enhanced Mathematical Rigor: An Addendum to the Discovery of New Laws of Conservation and Uncertainty. Cambridge University.(2025-06-30). https://doi.org/10.33774/coe-2025-hmk6nI