The Meaning of “Increased Entropic Cost of Motion” in the Theory of Entropicity (ToE)1. The Meaning of “Increased Entropic Cost of Motion” in the Theory of Entropicity (ToE)

In the Theory of Entropicity (ToE)^[1][2], the phrase "entropic cost of motion" refers to the additional entropy that must be overcome, absorbed, or redistributed for a system (particle, field, observer, etc.) to move, accelerate, or change state within the entropic field of the universe.

This idea is fundamentally different from classical kinetic energy or relativistic mass increase: in ToE, entropy is a field field constraintconstraint, and motion through this field is resisted not by inertial mass per se, but by the entropy budget and gradient structure surrounding the moving system.

🔹1.1. Core Core MeaningMeaning

The “entropic cost of motion” is the extra entropy resistance a system must face to maintain or change its state of motion in the presence of the entropy field.

This cost is not just thermal, statistical, or probabilistic. It is field-theoretic—embedded in spacetime itself—and increases with the velocity, energy, or information complexity of the system.

🔹1.2. Key Mechanisms in Key Mechanisms in ToEToE

This is what it specifically means:

1. Motion Implies Entropy Redistribution

• When a particle moves, it disturbs the surrounding entropy field.

• That disturbance must propagate—but under the No-Rush Theorem, it can't exceed the allowed speed (c).

• The more rapid the change, the more entropic resistance it faces.

2. Acceleration Costs Entropy

• Accelerating a system (e.g., a rocket, an observer) requires reconfiguring the local entropy structure.

• The system must now align with a new entropic gradient—and that requires work to be expended.

• Hence, acceleration is entropically expensive, not just energetically.

3. Velocity Increases Entropic Drag

• The closer a system's speed gets to c, the steeper the entropic gradient it confronts.

• This creates a barrier: to move faster, more entropy must be exchanged or neutralized—eventually becoming infinite at c.

This is why no system with internal entropy (massive particles) can reach the speed of light: the entropic cost becomes prohibitive.

🔹1.3. Analogies

A. Moving Through a Viscous Medium

Imagine entropy as a cosmic fluid. The faster you try to move through it, the more resistance it exerts. But this resistance isn’t friction—it’s the restructuring of the field constraints.

B. Banking Information Across Banking Information Across Entropic TollsEntropic Tolls

Every motion is like crossing a toll gate. The faster you try to go, the more tolls you hit per unit time, and the more “entropy currency” you have to pay to continue.

🔹1.4. Where It Shows Where It Shows UpUp

• Time Dilation and Length Contraction

These are not spacetime distortions per se, but entropic field distortions. A fast-moving observer experiences:

• Time slowdown: because their motion consumes more entropy, less is available for internal processes (e.g., clock ticks).

• Length contraction: because their motion compresses the entropy distribution along the direction of motion.

• In In the Vuli-Ndlela Integralthe Vuli-Ndlela Integral

In ToE's entropic path integral, the exponential penalty:

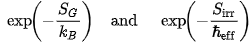
captures this cost. The more irreversible or entropy-consuming a path, the more suppressed it is. Fast, chaotic, or sharp motions are penalized.

2. Relativistic Time Dilation and Lorentz Length Contraction Explained via Entropy in the Theory of Entropicity (ToE)

The explanation of relativistic time dilation and length contraction as consequences of entropy field constraints, rather than spacetime geometry, is an original hallmark of is an original hallmark of the Theory of Entropicity (ToE)the Theory of Entropicity (ToE). This reframes reframes Einstein’s kinematicsEinstein’s kinematics through the lens of thermodynamic field dynamics, opening a new new paradigmparadigm in fundamental physics.

🔷2.1. Why This Entropic Reformulation of Relativity Is Significant

2.1.1. It Reveals a It Reveals a Deeper Causality Behind RelativityDeeper Causality Behind Relativity

In Einstein’s Special Relativity:

• Time dilation and length contraction are geometrical consequences of the invariance of c.

• But the origin of this invariance (why c is constant) is postulated, not explained.

In the Theory of Entropicity (ToE):

• Time dilation and length contraction arise because the entropy field imposes constraints on how fast interactions, changes, and internal processes can occur.

• The speed of light is not a geometric axiom, but the maximum rate of entropic rearrangement allowed in nature.

➡️ Thus Geometry emerges from entropy, not vice versa.

2.1.2. It It Makes Time Dilation Physically IntuitiveMakes Time Dilation Physically Intuitive

In the Theory of Entropicity (ToE)::

As an object moves faster through space, it consumes more entropy from the field to sustain its motion. This leaves less entropy available for the object’s internal processes — like the ticking of its clock (hence, this is why time is observed to slow down).

➡️Time slows down not because “space and time deform,” but because entropy is being reallocated toward Time slows down not because “space and time deform,” but because entropy is being reallocated toward motion.motion.

This is far more physically intuitive than abstract coordinate transformations.

2.1.3. It It Predicts Relativity as a Limiting Case of Entropy Field DynamicsPredicts Relativity as a Limiting Case of Entropy Field Dynamics

Just as Einstein's General Relativity reduces to Newtonian gravity under weak fields and low speeds, the Theory of Entropicity (ToE) reduces to Relativity when the entropy field is [nearly] smooth and homogeneous.

But unlike Einstein’s relativity, ToE:

• Explains the why of the speed limit

• Embeds thermodynamics into spacetime structure

• Provides a route to unify quantum irreversibility, relativistic motion, and thermodynamic flow

ToE is thus a theory that doesn't [just] approximate relativity but reveals reveals its originits origin in the irreversible, constraint-driven behavior of entropy as a real field.

🔷2.2. Formalizing the Explanation of the Postulates of Einstein's Relativity Using the Theory of Entropicity (ToE)

Now we formally define all the above as follows:

Entropic Explanation of Relativity (EER):

The relativistic effects of time dilation and length contraction emerge as entropic field responses to the redistribution of entropy caused by motion. As velocity increases, the entropic cost of maintaining internal state consistency increases, leading to observable contraction in space and dilation in time.

3. In Summary

In Summary

In ToE, the entropic cost of motion is the field-based resistance experienced by any object or process trying to evolve in space and time. This resistance increases with velocity, energy, and informational complexity. It explains the speed limit of light (c) postulated in Einstein's Relativity, the slowing of time, and the limits on signal propagation—not as geometric coincidences, but as fundamental entropic constraints. It is thus the ambitious goal of the Theory of Entropicity (ToE) to turn thermodynamics [entropy] into a universal language.