No physical interaction can occur instantaneously; every process requires a finite, nonzero duration; implying that Nature cannot be rushed. ^{[1][2][7][8][9]}

Entropy as a Dynamic Field

• Field Promotion
  
  Traditionally, entropy S is a global quantity defined for systems in or near equilibrium. ToE promotes entropy to a spacetime-dependent scalar field S(x).

• Couplings and Dynamics
  
  Gradients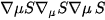 and time derivatives  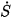appear directly in the equations of motion for matter and geometry, sourcing forces and mediating interactions analogously to the electromagnetic potential or the gravitational metric.

Statement of the No-Rush Theorem

• Finite Interaction Time
  
  Because interactions proceed via the exchange or redistribution of entropy^[7][8][9]—through informational currents, microscopic reconfigurations, or entropic gradients—they cannot “turn on” in zero time.

• Minimum Entropic Interval
  
  There exists a lower bound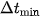 ​, determined by the intrinsic “stiffness” of the entropic field^[11][12] (often linked to a Fisher-information term in the action), below which no causal influence can propagate.

Physical Implications

1. Causality and Speed Limits

   • Provides an entropy-based origin for why no influence can travel faster than a maximum speed, complementing relativity’s light-cone structure.

      

2. Gravity and Inertia

   • Bodies respond not only to spacetime curvature but also to the finite “ramp-up” time of entropic forces, potentially modifying inertial behavior at very small scales.

3. Quantum Processes and the Arrow of Time

   • Embeds irreversibility at a fundamental level. Quantum transitions, measurements, and decoherence processes require a nonzero duration, reinforcing the unidirectional flow of time.

Connections to Existing Concepts

• Decoherence in Open Quantum Systems
  
  Quantum coherence^[13] is lost over finite timescales as systems entangle with their environment—an entropy-driven process.

• Entropic Forces
  
  Similar to how entropy gradients drive polymer elasticity or Verlinde’s^[14] emergent gravity, the No-Rush Theorem ensures these gradients cannot act instantaneously.

• Information-Theoretic Limits
  
  The minimum interaction time aligns with the time needed to transfer or distinguish quanta of information, linking ToE to information-geometry and Fisher information.^[15][16]

Beyond Traditional Physics

• Challenging Instantaneous Assumptions
  
  Many idealized models—instantaneous collisions, ideal springs, certain gauge approximations—assume zero-time interactions. The No-Rush Theorem treats these as approximations valid only when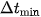 is negligibly small compared to experimental timescales.

• Experimental Predictions
  
  Subtle delays or frequency-dependent response times in high-precision tests of fundamental forces could reveal the finite interaction interval predicted by ToE.

1. Historical Development

• Early Motivation
  
  Obidi’s original insight came from analyzing attosecond‐scale entanglement formation experiments, which implied a minimum interaction interval beyond the Planck time.

• Formal Statement (2025)
  
  The theorem was codified in Obidi’s Master Entropic Equation (MEE) framework, linking the minimum time to a Fisher‐information “stiffness” in the entropy field.

• Subsequent Extensions
  
  Later works extended the theorem to include temperature‐dependent bounds and to apply in curved spacetime near black‐hole horizons.

2. Mathematical Formulation

• Entropy Field Dynamics
  
  The entropy field $S\left(x\right)$ obeys a second‐order differential equation derived from the MEE action.

• Fisher‐Information Bound
  
  A term

  −λ2kB2 e−S/kB gμν ∇μS ∇νS -\frac{\lambda}{2k_B^2}\,e^{-S/k_B}\,g^{\mu\nu}\,\nabla_\mu S\,\nabla_\nu S−2kB2​λ​e−S/kB​gμν∇μ​S∇ν​S

  endows $S$ with an intrinsic “stiffness.” The resulting dispersion relation implies a minimum group‐velocity cutoff.

• Derived Minimum Time
  
  One finds

  Δtmin⁡=λkB2 ⟨(∇S)2⟩ \Delta t_{\min} = \sqrt{\frac{\lambda}{k_B^2\,\langle(\nabla S)^2\rangle}}Δtmin​=kB2​⟨(∇S)2⟩λ​​

  in flat spacetime, generalizable to Δtmin⁡(T,R)\Delta t_{\min}(T,R)Δtmin​(T,R) when including temperature $T$ and curvature radius $R$.

3. Physical Interpretation

• Causality from Entropy
  
  Beyond the relativistic light‐cone, the No-Rush bound provides a complementary causality limit rooted in information transfer rates.

• Entropic “Ramp-Up”
  
  Forces—gravitational, electromagnetic, strong and weak—must “build up” via entropy redistribution before reaching their full strength.

• Relation to Decoherence
  
  Environmental decoherence times in quantum systems mirror the No-Rush interval, tying information loss to interaction onset.

4. Cosmological Implications

• Early Universe Dynamics
  
  During reheating, entropy production rates set a lower bound on reaction times, influencing baryogenesis and dark‐matter freeze-out.

• Inflationary Constraints
  
  The theorem implies that fluctuations below Δtmin⁡\Delta t_{\min}Δtmin​ cannot decohere, placing a cutoff on the primordial power spectrum.

• Bounce and Cyclic Models
  
  In entropic‐cosmology scenarios, the minimum time moderates the transition rate between contraction and expansion phases.

5. Experimental Tests and Observational Signatures

• High-Precision Force Measurements
  
  Frequency-dependent response delays in torsion-balance experiments could reveal Δtmin⁡\Delta t_{\min}Δtmin​-scale effects.

• Quantum Optics
  
  Ultrafast pump–probe experiments probing entanglement formation may detect nonzero lower bounds on correlation buildup time.

• Astrophysical Transients
  
  Time-resolved observations of black-hole quasi-normal ringing may exhibit slight phase lags attributable to entropic “switch-on” delays.

6. Criticisms and Debates

• Scale of Δtmin⁡\Delta t_{\min}Δtmin​
  
  Some argue that Δtmin⁡\Delta t_{\min}Δtmin​ is so small (attoseconds or less) as to be experimentally irrelevant.

• Overlap with Relativistic Causality
  
  Critics question whether a separate entropy‐based bound is distinguishable from the light‐cone constraint.

• Defining Local Entropy
  
  The assumption of a well-defined local entropy density $S\left(x\right)$ outside equilibrium remains debated in non-equilibrium thermodynamics.

7. Open Questions

• Temperature and Curvature Dependence
  
  How does Δtmin⁡\Delta t_{\min}Δtmin​ vary with local temperature, pressure, and spacetime curvature in strong‐gravity regimes?

• Quantum Gravity Integration
  
  Can the No-Rush bound be derived from a full quantum‐gravitational theory, such as loop quantum gravity or string theory?

• Relation to Information Speed Limits
  
  Is there a precise connection between Δtmin⁡\Delta t_{\min}Δtmin​ and bounds like the Margolus–Levitin theorem or channel‐capacity limits in quantum information theory?

8. Related Principles

• Lieb–Robinson Bound (many-body quantum systems)

• Margolus–Levitin Theorem (quantum speed limits)

• Entropic Force Hypotheses (Verlinde, Padmanabhan)

• Decoherence Timescales in open quantum systems

9. See Also

Summary

The No-Rush Theorem elevates the principle “nothing happens instantly” into a precise, quantifiable dictum: the entropic field’s dynamics enforce a strict, nonzero lower bound on all interaction times, reshaping our understanding of causality, force mediation, and irreversibility across physics. "Nature cannot be rushed."