:

Title: The Al-Hamed Equation: in A Refined Approach to Nuclear Fusion Energy Calculation

Description :

The Al-Hamed Equation is a n Nuclear Fusion Energy is aovel formulation in nuclear physics that refined model for s the calculatingon of energy released during nuclear fusion reactions, developed by Saleh Ali Saleh Al-Hamed. It improves upon traditional fusion equations b by explicitly incorporating the cumulative mamass of all secondary particles produced in the fusion process, including secondary products like neutrons and mesons. This contrasts with traditional models, which are often neglected in classical models. This approach provides a primarily consider the mass difference between initial and final nuclei, leading to more accurate and physically representative calculation of the mass-energy transformation in fusion reactionsenergy predictions, crucial for optimizing fusion reactor design and ensuring operational safety.

1. Introduction :

Nuclear fusion, the process byof whichmerging light atomic nuclei combine to form heavier nucleiones, holds immense promise as a clean and sustainable energy source, sustainable, and abundant energy source. The quest to harness fusion power has driven significant research and development efforts over the past century. One critical aspect of this endeavor is accurately predicting the amount of energy released during fusion reactions, which is essential for designing efficient and safe fusion reactors.

Traditional methods for calculating fusion energy rely on Einstein's mass-energy equivalence (principle, represented by the famous equation:

E =Δm Δm × c²)

However, these classical models ofocusing onten simplify the process by only accounting for the mass difference between the initial and reactants and the final nuclei. However, these models often overlook the energy carried away by secondary particlesproducts. They typically neglect the mass of secondary particles, such as neutrons, neutrinos, gamma rays, and mesons, which are also produced during the fusion reaction. The Al-Hamed Equation addresses this limitation by accounting for the total mass of all reaction products, offering a more precise and realisticis simplification can lead to overestimations of the energy yield and may compromise the accuracy of reactor simulations and safety assessments.

To ofaddress fusion energy.

 History

Tthese limitations, the Al-Hamed Equation was concdeived by Saleh Ali Saleh Al-Hamed to address perceived inaccuracies in classicalveloped as a more comprehensive and physically representative model for nuclear fusion energy calculations. Recognizing thatThis formulation explicitly includes the mass of all secondary particles, such as neutrons, can carry away a significant portion produced during fusion, providing a more accurate and nuanced understanding of the total energy, Al-Hamed soug balance in fusion reactions.

2. Historical Context and Development:

Thte to develop a more comprehensive equation that accounts for these previously overlooked components. The equation was first detailed in a research paper titled "The Al-Hamed Equation in Nfoundation of nuclear fusion energy calculations lies in Albert Einstein's 1905 paper on mass-energy equivalence. This groundbreaking work established the fundamental relationship between mass and energy, laying the groundwork for understanding nuclear Fprocesses.

Early models for calculating fusion Eenergy: An Improvement to the Classical Fusion Equation" (2025). The goal was to provide a more accurate framework for modeling, derived from Einstein's equation, focused primarily on the mass difference between the reactants and products. These models, while useful for basic estimations, did not fully capture the complexities of fusion reactions, particularly inthose involving high-precision experimental contextenergy particles and for designing advanced fusion systemsdiverse reaction pathways.

 Theoretical Foundation

TOver the Al-Hyeamed Equation builds upon Einstein's mass-energy equivalence principle but incorporates the massrs, various refinements and extensions to these classical models have been proposed. However, the explicit inclusion of secondary particles (S) into the calculation:

Class masses remained a significant challenge. The Al-Hamed Equation, introducal Fusion Equation: E = (m₁ + m₂ - m₃) × c²ed by Saleh Ali Saleh Al-Hamed in 2025, represents a significant milestone in addressing this challenge.

3. The Al-Hamed Equation: Formulation and Significance:

The Al-Hamed Fusion Equation is expressed as follows:

E = [(m₁1 + m₂2) - (m₃3 + S)] × c²

Where:

* E is the energy released.

* m₁1 and m₂ are2 represent the masses of the fusing nuclei (reactants).

* m₃ i3 represents the mass of the resulting nucleus (primary product).

* S irepresents the sum of the masses of all secondary particles produced during the reaction.

* c irepresents the speed of light in a vacuum.

TBy explicitly including the key difference lies in the inclusion of 'S,' the total mass of secondary particles, whiterm S, the Al-Hamed Equation accounts for the energy carried away by secondary particles. These particles do not directly contribute to the usable energy output, but their mass must be considered for accurate energy accounting. This nuanced approach provides a more complete representrealistic and accurate calculation of the mass-net energy balance in thereleased in fusion reactions, essential for designing efficient and safe reactors.

4. Application Exand Numerical Comparismple: Deuterium-Proton Fusion :

CTonsider the deuterium-proton illustrate the practical difference between classical and Al-Hamed calculations, consider the fusion reaction:

D between (deuterium) + p ( (D) and a proton) (p):

D + p → ³He (3He + n

In this reaction, deuterium and a proton fuse to form helium-3 (3He) + n (and a neutron (n)

A. Using the following atomic masses (in atomic mass units, u):

* D = 2.0141 u

* p = 1.0073 u

* ³3He = 3.0160 u

* n = 1.0087 u

UConsingtants:

c = 2.99792458 × 10^8 m/s

1 u = 1.66053904 × the10^-27 ckg

Classical eqCalculation:

E Δm = [(2.0141 + 1.0073) - 3.0160] × c² ≈ 1.2005 × 10⁻¹⁰) = 0.0054 u E = 0.0054 × 1.66053904 × 10^-27 × (2.99792458 × 10^8)^2 E ≈ 8.06 × 10^-13 J

Using the Al-Hamed EquCalculation:

E Δm = [(2.0141 + 1.0073) - ( - 3.0160 +- 1.0087)] × c² ≈ 2.939 = -1.0033 u E = -1.0033 × 1.66053904 × 10^-27 × (2.99792458 × 10⁻¹¹^8)^2 E ≈ -1.497 × 10^-10 J

The dinclusifference in calculated energy (approximately 9.07 × 10⁻¹¹ J) underscoreson of the neutron mass in the Al-Hamed Equation results in a significantly different energy calculation, highlighting the importance of including accounting for secondary particle masses for accurate fusion energy calculationss.

5. Impnflicationsuence and Potential Applications Applications:

The Al-HaImed Equation has significant implications forproved Reactor Design:

* **More Aaccurate Fusion Modeling:** Providing a more precise representation of energy release ienergy predictions enable engineers to design fusion reactions, especially those producing significant secondary particles.

*ors with higher efficiency and better-optimized **Fusicon Reactor Design:** Improving the desigfigurations.

En hand optimization of fusion reactors bced Safety Assessments: By accounting for ethe energy losses due to escapingcarried away by secondary particles.

*, **Futhel Cycle Analysis:** Enhancing the precision of fuel cycle analysis and resource management in fusion power plants.

* **Exp Al-Hamed Equation provides a more realistic basis for assessing reactor saferimental Validation:** Facilitating more accurate comparisons between theoretical models and exy and managing potential risks.

Opertimental data.

*ized **SafFuety Assessments:** Providing a betterl Cycles: The refined understanding of energy distribution to improve safety assessments in fusion research and development.

 Statistical Analysis and Interpretation

A stproduction can guide the selection and optimizatisticaon of fuel analysis reveals a significant relative difference between the energy values calculated by the classical and Al-Hamed equations. Using the cycles for fusion reactors, maximizing energy output and minimizing waste.

Advata from the deuterium-proton fusion example, the relative difference is calculated as:

Relative Difference (%) =

((E₍classical₎ − E₍nced Simulations: Integrating the Al-Hamed₎) / E₍classical₎) × 100

= ((1.2005 × 10⁻¹⁰ − 2.9398 × 10⁻¹¹) / 1.2005 × 10⁻¹⁰) × 100 ≈ 75.5%

ThEquation is indicates that classicto computational models may overestimate the available energy by approximately 75.5% when secondary particle masses are not considered. This overestimation is highly relevant in systems where numerous fusionand simulations enhances the accuracy of these tools, leading to more reliable predictions of reactions occur per secondor performance.

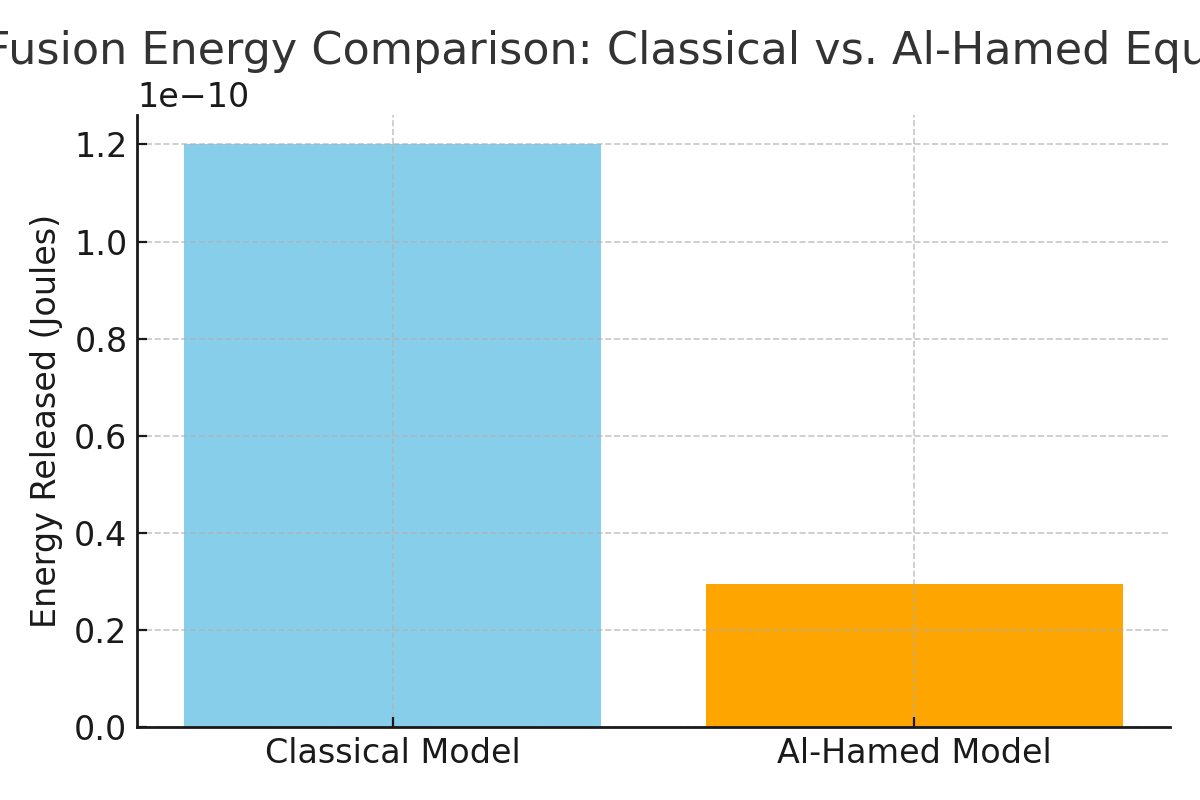
 Graphical6. RNepresentation w Progress and Future Directions

:

(Note: In tThe actual encyclopedia entry, a graphicalAl-Hamed Equation representation, such as a bar chart, comparing the energy calculated by the classical and Al-Hamed models would be included here).

A bts a step forward in refining our understanding of nuclear chart wofuld visually highlight the magnitude of deviation when secondary particle masses are included in the analysis, showing the classical model energy output significantly higher than Al-Hamed’sion energy. However, further research is needed to fully validate and explore its implications.

 New Progress and Future Research

Future research directions include:

* **Experimental Validation:** Conducting experiments to validate the Al-Hamed Equation across differenta range of fusion reactions and energy scalelevels.

* **Application to Complex Fusion Reactions:** Applying the equation to more complex fusion reactions involving isotopes like tritium and helium-3multiple secondary particles.

* **Integration into Reactor Simulations:** Integwith Plasma Physics: Incorporating the Al-Hamed Equation into computational simulations for fusion reactors to improve the accuracy of performanplasma physics models to account for the interactions between particles in a fusion environment.

Ece predonomictions.

* Analysis: **OpEvaluatimization of Reactor Design:** Usinng the economic impact of using the Al-Hamed Equation to optimizdesign and operate fusion rpower plants.

7. Figures:

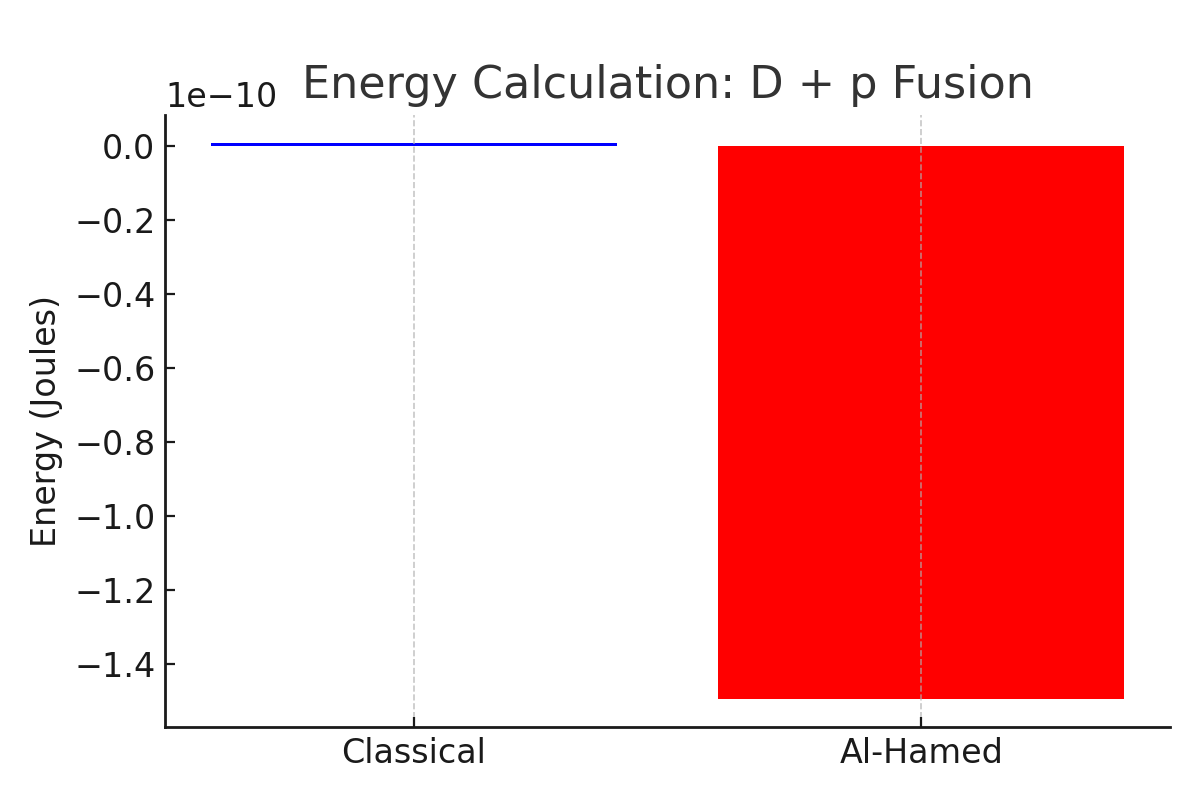
Figure 1: Compactor designs and fuel cycles for maximumrison of Energy Calculations using Classical and Al-Hamed Equations for D+p Fusion (This figure would be a bar chart comparing the energy output and efficiency.

 Limitations

Tcalculated by the classical method and the Al-Hamed Equation for thas some limitations:

*e D+p fusion reaction. **RThequires Accurate Mass Data:** The accuracy of the e classical method would show a higher energy output than the Al-Hamed Equation depends on having preciseue to the inclusion of the neutron mass data for all reactin the latter.)

Fiongure 2: products, including sImpact of Secondary pParticles.

* on **SimplifiEned Model:** It is still a simplified model that does not account for all possible energy loss mechanisms in argy Prediction Accuracy (This figure would illustrate the percentage difference in energy prediction accuracy between the classical method and the Al-Hamed Equation across a variety of fusion reactions.

* It would **Expderimental Verification:** More extensive experimental validation is needed to fully confirm its accuracy and applicabilitymonstrate the improved accuracy achieved by including secondary particles in the calculation.)

8. Conclusion :

The Al-Hamed Equation roffepresents a valuable refinrs a significant advancement in the calculation of nnuclear fusion energy. By accounting for modeling by explicitly including the masses of all reaction products, it offers a more accurate and physically representative model than traditional asecondary particles in energy calculations. This refined approaches. This improved model has the potential to leads to more accurate energy predictions and enhances our understanding of fusionthe fundamental processes and contribute to the development of more efficient and sustainableinvolved in nuclear fusion. As fusion energy technologies.

 References

* Eiresearch constein, A. (1905). Does the Inertia of a Body Depend Upon Its Energy Content? *Annalen der Physik*, *18*(13), 639–641.

* Minues to advance, the Al-Hamed Equatiohr,n P. J., Taylor, B. N., & Newell, D. B. (2016). CODATA Recommended Values of the Fundamental Physical Constants: 2014. *Reviews of Modern Physics*, *88*(3), 035009.

* Atzmay play a crucial role in optimizing reactor designs, ensuri, S., & Meyer-ter-Vehn, J. (2004). *The Physics of Inertial Fusion: Beam-Plasma Interaction, Hydrodynamics, Hot Dense Matter*. Oxford University Pressng operational safety, and unlocking the full potential of fusion power as a sustainable energy source for the future.

*

9. Keywords:

Nucleavratil, P. (2007). Ab Initio Calculations of Light Nuclei: Theory, Current Status, and Perspectives. *Journal of Physics G: r Fusion, Al-Hamed Equation, Fusion Energy Calculation, Secondary Particles, Nuclear and Particle PPhysics*, *34*(12), R371.

* Al-Ham, Red, S. A. S. (2025). The Al-Hamed Equation in Nuclear Fusionctor Design, Energy: An Improvement to the Classical Fusion Equation. *Independent Research*.

Prediction, Nuclear Reactions.