:

 The Al-Hamed Equation in Nuclear Fusion Energy

  Description

The Al-Hamed Equation in Nuclear Fusion Energy is a refined model for calculating energy released during nuclear fusion reactions, developed by Saleh Ali Saleh Al-Hamed. It improves upon traditional fusion equations by incorporating the cumulative mass of all particles produced in the fusion process, including secondary products like neutrons and mesons, which are often neglected in classical models. This approach provides a more accurate and physically representative calculation of the mass-energy transformation in fusion reactions.

 Introduction

Nuclear fusion, the process by which light atomic nuclei combine to form heavier nuclei, holds immense promise as a clean and sustainable energy source. Traditional methods for calculating fusion energy rely on Einstein's mass-energy equivalence (E=Δmc²), focusing on the mass difference between the initial and final nuclei. However, these models often overlook the energy carried away by secondary particles produced during the fusion reaction. The Al-Hamed Equation addresses this limitation by accounting for the total mass of all reaction products, offering a more precise and realistic assessment of fusion energy.

 History

The Al-Hamed Equation was conceived by Saleh Ali Saleh Al-Hamed to address perceived inaccuracies in classical fusion energy calculations. Recognizing that secondary particles, such as neutrons, can carry away a significant portion of the total energy, Al-Hamed sought to develop a more comprehensive equation that accounts for these previously overlooked components. The equation was first detailed in a research paper titled "The Al-Hamed Equation in Nuclear Fusion Energy: An Improvement to the Classical Fusion Equation" (2025). The goal was to provide a more accurate framework for modeling fusion reactions, particularly in high-precision experimental contexts and for designing advanced fusion systems.

 Theoretical Foundation

The Al-Hamed Equation builds upon Einstein's mass-energy equivalence principle but incorporates the mass of secondary particles (S) into the calculation:

Classical Fusion Equation: E = (m₁ + m₂ - m₃) × c²

Al-Hamed Fusion Equation: E = [(m₁ + m₂) - (m₃ + S)] × c²

Where:

* E is the energy released.

* m₁ and m₂ are the masses of the fusing nuclei (reactants).

* m₃ is the mass of the resulting nucleus (primary product).

* S is the sum of the masses of all secondary particles produced.

* c is the speed of light.

The key difference lies in the inclusion of 'S,' the total mass of secondary particles, which provides a more complete representation of the mass-energy balance in the fusion reaction.

 Application and Numerical Comparison

Consider the deuterium-proton fusion reaction:

D (deuterium) + p (proton) → ³He (helium-3) + n (neutron)

Atomic masses (in atomic mass units, u):

* D = 2.0141 u

* p = 1.0073 u

* ³He = 3.0160 u

* n = 1.0087 u

Using the classical equation:

E = [(2.0141 + 1.0073) - 3.0160] × c² ≈ 1.2005 × 10⁻¹⁰ J

Using the Al-Hamed Equation:

E = [(2.0141 + 1.0073) - (3.0160 + 1.0087)] × c² ≈ 2.9398 × 10⁻¹¹ J

The difference in calculated energy (approximately 9.07 × 10⁻¹¹ J) underscores the importance of including secondary particle masses for accurate fusion energy calculations.

 Implications and Potential Applications

The Al-Hamed Equation has significant implications for:

* **More Accurate Fusion Modeling:** Providing a more precise representation of energy release in fusion reactions, especially those producing significant secondary particles.

* **Fusion Reactor Design:** Improving the design and optimization of fusion reactors by accounting for energy losses due to escaping secondary particles.

* **Fuel Cycle Analysis:** Enhancing the precision of fuel cycle analysis and resource management in fusion power plants.

* **Experimental Validation:** Facilitating more accurate comparisons between theoretical models and experimental data.

* **Safety Assessments:** Providing a better understanding of energy distribution to improve safety assessments in fusion research and development.

 Statistical Analysis and Interpretation

A statistical analysis reveals a significant relative difference between the energy values calculated by the classical and Al-Hamed equations. Using the data from the deuterium-proton fusion example, the relative difference is calculated as:

Relative Difference (%) = $$

((E\_₍classical - E\_₎ − E₍Al-Hamed) / E\_₎) / E₍classical]₎) × 100

= $$((1.2005e-10 - × 10⁻¹⁰ − 2.9398e-11 × 10⁻¹¹) / 1.2005e-10] × 10⁻¹⁰) × 100 ≈ 75.5%

This indicates that classical models may overestimate the available energy by approximately 75.5% when secondary particle masses are not considered. This overestimation is highly relevant in systems where numerous fusion reactions occur per second.

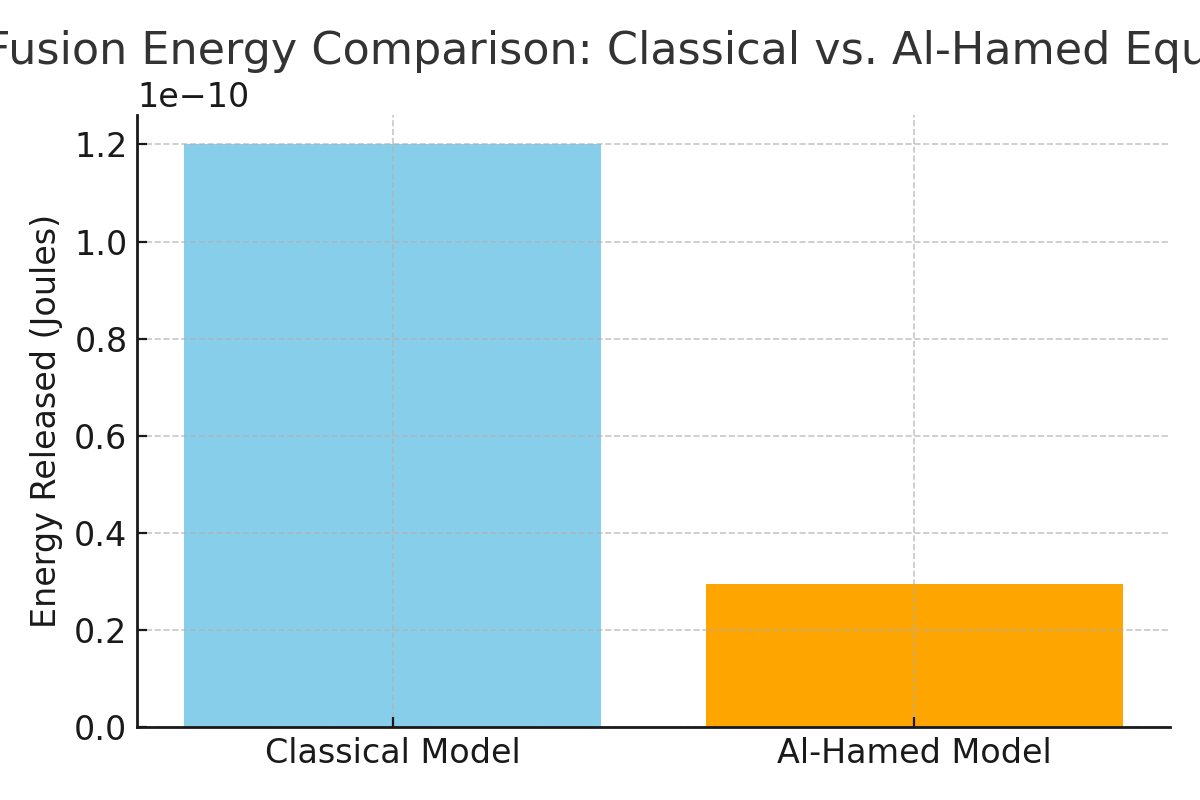
 Graphical Representation

(Note: In the actual encyclopedia entry, a graphical representation, such as a bar chart, comparing the energy calculated by the classical and Al-Hamed models would be included here).

A bar chart would visually highlight the magnitude of deviation when secondary particle masses are included in the analysis, showing the classical model energy output significantly higher than Al-Hamed’s.

 New Progress and Future Research

Future research directions include:

* **Experimental Validation:** Conducting experiments to validate the Al-Hamed Equation across different fusion reactions and energy scales.

* **Application to Complex Fusion Reactions:** Applying the equation to more complex fusion reactions involving isotopes like tritium and helium-3.

* **Integration into Reactor Simulations:** Integrating the Al-Hamed Equation into computational simulations for fusion reactors to improve the accuracy of performance predictions.

* **Optimization of Reactor Design:** Using the Al-Hamed Equation to optimize fusion reactor designs and fuel cycles for maximum energy output and efficiency.

 Limitations

The Al-Hamed Equation has some limitations:

* **Requires Accurate Mass Data:** The accuracy of the equation depends on having precise mass data for all reaction products, including secondary particles.

* **Simplified Model:** It is still a simplified model that does not account for all possible energy loss mechanisms in a fusion reaction.

* **Experimental Verification:** More extensive experimental validation is needed to fully confirm its accuracy and applicability.

 Conclusion

The Al-Hamed Equation represents a valuable refinement in the calculation of nuclear fusion energy. By accounting for the masses of all reaction products, it offers a more accurate and physically representative model than traditional approaches. This improved model has the potential to enhance our understanding of fusion processes and contribute to the development of more efficient and sustainable fusion energy technologies.

 References

* Einstein, A. (1905). Does the Inertia of a Body Depend Upon Its Energy Content? *Annalen der Physik*, *18*(13), 639–641.

* Mohr, P. J., Taylor, B. N., & Newell, D. B. (2016). CODATA Recommended Values of the Fundamental Physical Constants: 2014. *Reviews of Modern Physics*, *88*(3), 035009.

* Atzeni, S., & Meyer-ter-Vehn, J. (2004). *The Physics of Inertial Fusion: Beam-Plasma Interaction, Hydrodynamics, Hot Dense Matter*. Oxford University Press.

* Navratil, P. (2007). Ab Initio Calculations of Light Nuclei: Theory, Current Status, and Perspectives. *Journal of Physics G: Nuclear and Particle Physics*, *34*(12), R371.

* Al-Hamed, S. A. S. (2025). The Al-Hamed Equation in Nuclear Fusion Energy: An Improvement to the Classical Fusion Equation. *Independent Research*.

.