The use of quantum optical systems for investigation in General Relativity ad related theories, of which General Relativity is the weak-field limit is exposed; the analyses are based on the comparison of the properties of Astrophysical systems inferred form the quantum-optics techniques, which can compare Planck-scale physics.
- Blackhole spacetimes
- Active Galactic Nuclei
- discs
- dust
- gaseous material
- jets
- sparticles
- geometrical phase
- modified dispersion relations
1. Introduction
The comparison between the items of information gained after quantum-optical-devices experiments about Astrophysical phenomena and about cosmology of particle physics is proposed from [1]. The origin of galaxies was discriminated [2] after semianalytic calculations as far as the growth of supermassive black holes are concerned according to the schemes of seeding models and pertinent accretion modes according to the abundances and to the maximum masses of the formers.
The behaviours of the celestial bodies high-redshift galaxies can be verified according to the pressure and to the energy [3].
The measurements of the frequencies of the periapsis and those of the Lense–Thirring precessions allows one to infer items of information about the evolution of galactic structures and that of their compact objects in the vicinity of the galaxy centers [4], as well as to discover new General-Relativistic phenomena.
The observation range and the source rate of gravitational radiation in the leading-order quadrupole is used to follow the evolution of binary systems; within this framework of analysis, it is crucial that signal-to-noise ratio and standard deviation should be available at the sufficient accuracy to render the first Post-Newtonian order not needed [5]; this is achieved by means of a single interferometer. In this manner, the qualities of particles and those of their aggregation states are intended for the further modellization of galaxies and of celestial bodies.
One of the purposes of the presentation is the use of description of space-times in Astrophysical phenomena, which can be investigated after quantum-optics devices, whose exploration ranges allow to compare with scales proper of the Planck length and larger ones, at which it is possible to individuate new particles.
Stellar spectroscopy and velocimetry can be achieved after a laser-based system [6] which governs the calibration of interferometers and accounts for dispersive technologies.
The milliarcsecond-emission regions of Active Galactic Nuclei (AGN’s) are demonstrate to be reconducted to the mass function of quasar blackholes [7]; the anisotropy of UV emission i.e. of the interstellar medium is controlled after the presence of two identical telescopes. In order to establish a lower bound of the size of the region, the ratio of the total emission flux with one measured after a single instrument allows one to determine a lower bound for the size of the region. At the considered frequencies, the interferometer-based baseline s used to delineate the size of the emitting region. The star background and/or the continuum light scattered at from the nucleus are investigated as far as the continuum spectrum is concerned.
The off-set of one single baseline interferometer can be determined after the use of three telescopes [8]: the technique is apt for calculating the position o a point-like source.
The very-long-baseline interferometers can be exploited as from [9] i order to perform measurements without the need of phase-referencing preparation especially set.
The Sagnac-Fabry-P´ erot interferometer is explained to be a devise apt for both gravitational-waves detection and particle-Physics experiments [10].
The use of quantum optical systems gives rise to the possibility to study both the properties of particles and those of the possible quantum-gravitational features of the spacetime, i.e. phenomena occurring at scales larger than the Planckian scale can be considered; accordingly, the analysis of Astrophysical phenomena can be compared to that of particles and spacetimes qualities [11][12][13][14]; as an example, the modification of the dispersion relations [15] can be used at the considered lenghtscales. The paper is organized as follows. In Section 2, the main outlines of Sky investigation are posed.
In Section 3, the discussion is enhanced, about how to establish the comparison with the phenomenon individuated beyond the quantum. In particular, the phenomena individuated, which take place at scales larger than the Planckian scales allow one to establish the comparison between the Astrophysical implementation of General Relativity and the related theories of which General relativity is the low-energy limit, i.e. also as far as new particle detection is concerned.
2. Sky Investigations
2.1. ’Post-Keplerian’ Objects
The analysis of the motion of pulsars around spinning blackholes allow one to infer the important items of information about spin and orientation of the blackhole object [16]: to this end, the pulsar is considered as a test particles in the Kerr blackholes spacetimes metric. Other ’Newtonian’ material in the galactic region is theoretised to produce ’Keplerian noise’ [17] which has to be not considered as due to the blackhole spacetimes metric.
In [18], S start are considered as following an almost-Keplerian behaviour on a background on which the Schwarzschild contributions can be isolated; distributions in the redshift measurements along the orbit of the star are described as more intensive at the pericenter, from whose items of information can be extracted about the blackhole spin-induced quadrupole moment.
If the hypothesis is made of a different background metric, the Hamiltonian to be considered is one consisting of several addends as
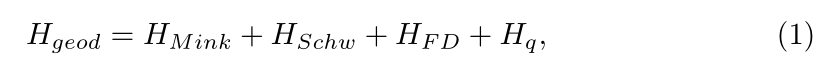
where flat spacetime Hamiltonian, the Schwarzschild Hamiltonian, the frame-dragging Hamiltonian, and the BH quadrupole moment are summed, respectively; it is crucial to remark that the Schwarzschild Hamiltonian is of the v 4 order, and both the frame-dragging Hamiltonian and the BH quadrupole moment one are of the v 6 order.
It is possible to consult the PN order in order to extract more items of description about a star which orbits of a Keplerian non-precessing order the galactic blackhole after simplifying the PN parameter β as β ≡ β(r;a)

with a the orbital major semiaxis, and with r s the Schwarzschild radius of the blackhole. It is possible to prove that the periapse shift ascribed to any type of dark matter is negligible at the chosen order.
The astrometric deviation δ x of a star which orbits the galactic blackhole implies the precession of the star a written as a function of the spin of the galactic blackhole χ and of a as
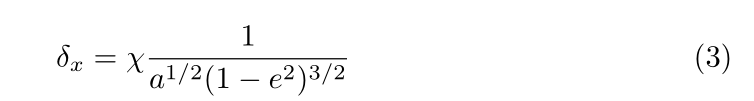
i.e. δ x ≡ δ x (χ,a) [19].
From [20][21][22], it is possible to infer that improvements of the derivatives of the orbital period of double neutron-star binaries can be gained after the use of wide-bandwidth coherent-dispersion devices.
The appropriate validations from binary pulsar systems [23] can induce the upper and/or lower bounds on the parameters and/or the parameter space of theories whose low-energy limit admits a low-energy limit which is different from GR, a different value for universal and/or a running Newton constant G and/or on the energy density of the low-frequency (limit of) gravitational waves. The equation of mass rate growth of a large celestial body dM/dt, being M the mass, is written as a function of the Keplerian orbital frequency of the large body which orbits a star of mass M ∗ at the orbital distance α , of the surface density of the field planetesimals ΣP
and of the radius of the larger body M as from [24][25] as

as pointed out in [26][27], being F G the gravitational focusing factor.
The magnitude of Neptune’s orbital expansion [28] has imposed a lower limit of about 5 AU; numerical results indicate the inclination distribution as sensitive to the rate of orbital evolution for giant planets, for which longer timescales of orbit evolution are correlated to higher inclinations.
For this, optical interferometers, infrared long-baseline and long-baseline (sub)millimeter interferometers, and high-sensitivity infrared observatories, are compared.
2.2. Verifying New Celestial Bodies by Alternative Experiments
Optical interferometers are use in the analysis of galaxies, celestial bodies in galaxies, and Newtonian material and Keplerian one in galaxies and and around them. Protoplanetary disks (i.e., around a star) are of particular interest for the information they carry for structure evolution [29] for the role of grains, dust, polycyclic aromatic hydrocarbons, and minerals. The presence of different kinds of dust is crucial in individuating different sizes for the formation of planets, as well as for their masses. The composition of dust and that of dust grains is used to reveal structure age. Spectral-analysis techniques are of use in revealing the composition in brain minerals, dust, dust grains, different kinds of dust, and crystalline and amorphous material. The grain growth [30] can be traced both by spectroscopy and after mm observation, i.e. according to grain size.
Dust-temperature determination can be reached after the analysis of different vibrations of the lattices of heavy ions, and/or groups of ions having low bond energies, and/or when the signal-to-noise ratio is high.
2.3. Items of Information Gained after the Transition Lines
The study of the CO transition lines CO(3-2) or CO(2-1) at submillimetric (submm) scales is demonstrated as predictive for the obtention of the interaction properties between a blackhole and a spheroidal celestial body (whose features are comparable with respect to the former) [31]; moreover, the procedure allows one to infer more insight about the role of quasars and that of quasar-like objects in the evolution of galaxies. A partial survey of galaxy emission lines is presented in [32].
Furthermore, the very same emission lines allow one to grasp items of information about the star-disc size: the increased ratio between the lines might delineate the features of an increase in the temperature the gas staying in the upper layers of the disc [33]. The azimuthal morphology can also be studied.
The spectral-energy distribution model can therefore be controlled; the study of the paradigms which imply these distribution models need to be implemented. gThe galaxy-forming areas can be studied after the CO (1-0) lines [34].
The study of gravitational lensing after CO lines was introduced in [35].
2.4. Laser Interferometers
From [36], the application of temperature-gradient techniques allows one to delineate the features of the detection of gravitational waves.
The Experiments [37][38][39][40][41][42] have pointed out that the improvement of the techniques with center-flat mirrors ans mesa-shaped beam optical cavities is necessary; as a result, the theormoelastic noise can be reduced after modifying the spaces of the mirrors [37].
The study of [43] indicates that the exploration of of a binary system of two stars with their own disc each is possible after the introduction of two angular variables; items of information can this way be acquired about the different angular positions of the two discs, and about the plane on which the light images are scattered. Accordingly, the emission of the stars can be molded as thermal; non-thermal paradigms are admitted as well, i.e. in case of gyrosynchrotron emissions. The investigation of the disc grain distribution and that of the dust-deposit probability can be achieved after the upper bound and the lower one for these processes are set after the possible non-negligible fractions of the millimeter flux.
The same device eventually provides one with a host of information [44] about the description of gaseous-CO emission in the far quasar, its mass, its density and its temperature: put lower bounds are put after the comparison of the CO line-flux ratios to those of a one-component large velocity gradient [45].
The centers of stars and of discs can be further modellised after the opportune continuous millimeter observation; the choice of the molecular transition to be followed allows one to grasp items of description of the core centers of stars and discs.
Appropriate continuum observations (at a millimeter scale) and the choice of molecular transitions allow to gain information about the core centers of stars and disks.
One technique which assures that the opacity properties of celestial bodies not be confused with the chemical effects ins tar forming regions is the mm-continuum observations [46].
A higher dust opacity index and a lowering of the optical depth enable one to take the hypothesis of the presence of grains at the core and/or at the disk centers. The molecular transition lines are chosen [47] as to recapitulate the qualities of the disc within the star formation. Baseline lengths a reused to improve the opacity index measurements [48][49][50].
2.5 Baseline Interferometers
The Sky pixelization proposed in [51] is efficient in detecting the statical properties of radio sources in the case of compact structures.
It is possible that the thinner structures are not resolved after a single-baseline interferometer.
The problems related to parametric instabilities in arm-cavity-mirror mechanical modes of interferometric detectors and the possible improvements are discussed in great detail in [52][53]. Different solution was proposed in [54] as far as the components of the piezoelectric are concerned.
The boundaries of the regions of dust evaporation in the discs of Young Stellar Objects is demonstrated to be resolved according to the process of grain formation after the techniques described in [55].
The issues concerning the avoidance of correlation between calibration summands, the azimuthal derivatives, and the equatorial angle are discussed in for single-baseline Earth-based interferometer [56]. correlations between calibration summands, and both azimuthal derivatives of the position-variable sky and equatorial angle.
2.6. The Role of the Redshift
In [44], the behaviours interstellar gas is discussed as far as the good success of the possibility to study that star formation and massive-blackhole formation can occur at the same cosmological epoch after the choice of the redshift, the choice of the transition lines and the brightness f the transition lines.
The temperatures of dust sublimation in the stellar photosphere can be investigated after optical photometry [57] after the opportune study of the spectral energy distributions as far as dust discs are concerned. As an important result, the radius can be parameterised as a function of the inverse square temperature.
3. Discussion: Mmore about Ccosmological Iinvestigation
The nuclei of active galaxies can be investigated after the resolution of the microarcoseconds, after which the characteristics of accretion discs of supermassive blackholes and those of their relativistic jets. This precision allows for the validation of schemes which trace back to star-formation times, and are related with small-scale investigation of quasar cores and that of AGN cores, as well as for the analysis of binary supermassive blackholes.
At this chosen precision, the astrometric detection of quasar parallasses is possible, which allows one to compare with the particle-induced effects [58][59][60][61][62][63][64][65].
The quantum properties of particles and the quantum features of space-time at Planckian lengths allow one to compare and to explore the semiclassical limit of quantum-gravitational phenomena. Quantum optical systems consisting in matter aggregation states allow to account for the quantum effects of phenomena which take place at scales larger than the Planckian, for laboratory- based experiments, and for observational surveys taking place in the background (Minkowski) flat spacetime [11][12][13][14].
The investigation of the first epoch of star formation and that of reionization can be pursued after Fourier-transforming the (time) delay to the (event) rate domain in order for weaker sources to be detected as well [66][67].
The square modulus of the Fourier transform is proven to completely characterise the laser-photocascade uses [68]; a criterion is provided with in [69] for discriminating between celestial bodies which emit in the IR spectrum.
The study of the effects of proton-proton collisions are provided with in [70][71].
This very same phenomenon can be compared with that of spacial broken O(3) symmetry originating form a geometrical (Berry) phase of the particles on curved spacetimes, from where the remaining degrees of freedom allow on to discriminate between sparticles according to the mass dispersion relation ∆m ij for masses m ij as
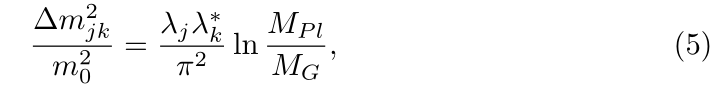
with λ i factorizing the (requested) coupling constant, m 0 being the mass of the common (standard-model) scalar (normalized to Planck mass M Pl ), and M G being the mass for a (massive) gravitational mode.
Interacting Further Particles
The existence is proposed of massive particles of masses M C compatible with the Planck mass, whose gravitational interaction can be able to modify the ordinary Newtonian gravity in the low-energy limit the the breach of higher-dimensional structures [72][73][74][75][72, 73, 74, 75].
The detection of sparticle masses such those form Eq. (5) is achievable after both silicon-based microelectromechanical systems [73][74][75][73, 74, 75] and cantilever experiments: the comparison of the two experimental techniques might enable one to discriminate between the presence of sparticles and Fifth-Force effects as from [76], where the way is opened for the comparison of experiments for the
verification of new particles.
The comparison of the analysis of signal reaching from the Sun can be compared with the detectors for Earth-based experiments looking for WIMPs of mass m W , m W 80Gev [77].
References
- Lecian, O.M., Alternative uses for quantum systems and devices. Symmetry 2019, 11, 462.
- Ricarte, A.; Natarajan, P. The observational signatures of supermassive black hole seeds. arXiv 2018, arXiv:1809.01177.
- Tamburello, V.; Capelo, P.R.; Mayer, L.; Bellovary, J.M.; Wadsley, J. Supermassive black hole pairs in clumpy galaxies at high redshift: delayed binary formation and concurrent mass growth. Mon. Not. Roy. Astron.Soc. 2017, 464, 2952-2962.
- Bender, P.L. Gravitational wave astronomy, relativity tests, and massive black holes. IAU Symp. 2010, 261, 240.
- Finn, L.S.; Chernoff, D.F. Observing binary inspiral in gravitational radiation: One interferometer. Phys. Rev. D 1993, 47, 2198.
- Hajian, A.R.; Behr, B.B.; Cenko, A.T.; Olling, R.P.; Mozurkewich, D.; Armstrong, J.T.; Pohl, B.; Petrossian, S.; Knuth, K.H.; Hindsley, R.B. Initial results from the USNO dispersed Fourier transform spectrograph. Astrophys. J. 2007, 661, 616. doi:10.1086/513181
- Voit, G.M. On nulling interferometers and the line-emitting regions of agns. Astrophys. J. 1997, 487, L109, doi:10.1086/310901
- Danchi, W.C.; Rajagopal, J.; Kuchner, M.; Richardson, J.; Deming, D The importance of phase in nulling interferometry and a three telescope closure-phase nulling interferometer concept. Astrophys. J.2006, 645, 1554, doi:10.1086/504511.
- Garrett, M.A. When you wish upon a star: Future developments in astronomical VLBI. ASP Conf. Ser. 2003, 306, 3.
- Chen, Y.B. Sagnac interferometer as a speed meter type, quantum nondemolition gravitational wave detector. Phys. Rev. D 2003, 67, 122004, doi:10.1103/PhysRevD.67.122004.
- Faizal, M.; Momeni, D. Universality of short distance corrections to quantum optics. arXiv 2018, arXiv:1811.01934.
- Frisch, O.R. Take a photon... Contemp. Phys. 1965, 7, 45.
- Bekenstein, J.D. Is a tabletop search for Planck scale signals feasible. Phys. Rev. D 2012, 86, 124040, doi:10.1103/PhysRevD.86.124040.
- Bekenstein, J.D. Can quantum gravity be exposed in the laboratory? Found. Phys. 2014, 44, 452, doi:10.1007/s10701-014-9779-z.
- Anandan, J.; Aharonov, Y. Geometry of quantum evolution. Phys. Rev. Lett. 1990, 65, 1697–1700.
- Zhang, F.; Saha, P. Probing the spinning of the massive black hole in the Galactic Center via pulsar timing: A full relativistic treatment. Astrophys. J. 2017, 849, 33.
- Barausse, E.; Cardoso, V.; Pani, P. Can environmental effects spoil precision gravitational-wave astrophysics? Phys. Rev. D 2014, 89, 104059.
- Angelil, R.; Saha, P.; Merritt, D. Towards relativistic orbit fitting of Galactic center stars and pulsars. Astrophys. J. 2010, 720, 1303.
- Waisberg, I.; Dexter, J.; Gillessen, S.; Pfuhl, O.; Eisenhauer, F.; Plewa, P.M.; Baubock, M.; Jimenez-Rosales, A.; Habibi, M.; Ott, T.; et al. What stellar orbit is needed to measure the spin of the Galactic centre black hole from astrometric data? Mon. Not. R. Astron. Soc. 2018, 476, 3600.
- Stairs, I.H. Testing general relativity with pulsar timing. arXiv 2003, arXiv:astro-ph/0307536.
- Jodrell Bank Observatory Pulsar Group, COBRA: Pulsar Documentation. 2001. pulsar/
- Swinburne Pulsar Group, The Caltech, Parkes, Swin-burne Recorder Mk II. 2002. Available online: http://astronomy.swin.edu.au/pulsar/ (accessed on 27 November 2002).
- Taylor, J.H. Pulsar timing and relativistic gravity. Philos. Trans. R. Soc. Lond. Ser. A 1992, 341, 117–134.
- Yagi, K.; Stein, L.C. Black hole based tests of general relativity. Class. Quant. Grav. 2016, 33, 054001.
- Wolf, S.; Malbet, F.; Alexander, R.; Berger, J.-P.; Creech-Eakman, M.; Duchene, G.; Dutrey, A.; Mordasini, C.; Pantin, E.; Pont, F.; et al.
- Safronov, V.S. Evolution of the Protoplanetary Cloud and Formation of the Earth and the Planets; Serie: NASA technical translation, F-677; Program for Scientific Translations: Jerusalem, Israel, 1972.
- Armitage, P.A. Astrophysics of Planet Formation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2010.
- Malhotra, R. The origin of pluto’s orbit: Implications for the solar system beyond neptune. Astron. J. 1995, 110, 420.
- Henning, T.; Meeus, G.; Dust processing and mineralogy in protoplanetary accretion disks. arXiv 2009, arXiv:0911.1010.
- Brauer, F.; Dullemond, C.P.; Henning, T., Coagulation, fragmentation and radial motion of solid particles in protoplanetary disks. Astronomy and Astrophysics 2008, 480, 859.
- Coppin, K.; Swinbank, A.M.; Neri, R.; Cox, P.; Alexander, D.M.; Smail, I.; Page, M.J.; Stevens, J.A.; Knudsen, K.K.; Ivson, R.J.; et al. Testing the evolutionary link between submillimetre galaxies and quasars: CO observations of QSOs at z 2. Mon. Not. R. Astron. Soc. 2008, 389, 45.
- Hippelein, H.; Maier, C.; Meisenheimer, K.; Wolf, C.; Fried, J.W.; von Kuhlmann, B.; Kummel, M.; Phelps, S.; Roser. H-J. Star forming rates between z=0.25 and z=1.2 from the CADIS emission line survey. Astron. Astrophys. 2003, 402, 65.
- Hughes, A.M.; Andrews, S.A.; Espaillat, C.; Wilner, D.J.; Calvet, N.; D’Alessio, P.; Qi, C.; Williams, J.P.; Hogerheijde, M.R. A spatially resolved inner hole in the disk around GM aurigae. Astrophys. J. 2008, 698, 131.
- Lisenfeld, U.; Braine, J.; Duc, P.A.; Brinks, E.; Charmandaris, V.; Leon, S. Molecular and ionized gas in the tidal tail in Stephan’s Quintet. Astron. Astrophys. 2004, 426, 471.
- Downes, D.; Solomon, P.M. Molecular gas and dust at Z = 2.6 in smm j14011+0252: a strongly lensed, ultraluminous galaxy, not a huge, massive disk. Astrophys. J. 2003, 582, 37.
- Barish, B.C.; Camp, J.; Kells, W.P.; Sanders, G.H.; Whitcomb, S.E.; Zhang, L.; Zhu, R.-Y.; Deng, P.; Xu, J.; Zhou, G.; et al. Development of large size sapphire crystals for laserinterferometer gravitational-wave observatory. IEEE Trans. Nucl. Sci. 2002, 49, 1233.
- D’Ambrosio, E.; O’Shaughnessy, R.W.; Strigin, S.; Thorne, K.S.; Vy-atchanin, S. Reducing thermoelastic noise in gravitational-wave interfer-ometers by flattening the light beams. arXiv 2004, arXiv:gr-qc/0409075.
- D’Ambrosio, E.; O’Shaughnessy, R.; Thorne, K.; LIGO Report Number G000223-00-D. Available online: http://admdbsrv.ligo.caltech.edu/dcc/ (accessed on 16 August 2000).
- Braginsky, V.; D’Ambrosio, E.; O’Shaughnessy, R.; Strigin, S.; Thorne, K.; Vyatchanin, S. LIGO Report Number G010151-00-R. Available online: http://admdbsrv.ligo.caltech.edu/dcc/ (accessed on 16 March 2001).
- Braginsky, V.; D’Ambrosio, E.; O’Shaughnessy, R.; Strigin, S.; Thorne, K.; Vyatchanin, S. LIGO Report Numbers G010333-00-D and G010297- 00-D. Available online: http://admdbsrv.ligo.caltech.edu/dcc/ (accessed on 15 August 2001).
- Braginsky, V.; D’Ambrosio, E.; O’Shaughnessy, R.; Strigin, S.; Thorne, K.; Vyatchanin, S. LIGO Report Number G020543-00-R. Available online: http://admdbsrv.ligo.caltech.edu/dcc/ (accessed on 6 September 2002).
- Braginsky, V.; D’Ambrosio, E.; O’Shaughnessy, R.; Strigin, S.; Thorne, K.; Vyatchanin, S. LIGO Report Number T030009-00-R. Available online: http://admdbsrv.ligo.caltech.edu/dcc/ (accessed on 23 January 2003).
- Duchene, G.; Menard, F.; Stapelfeldt, K.; Duvert, G. A layered edge-on circumstellar disk around HK Tau B. Astron. Astrophys. 2003, 400, 559–565.
- Bertoldi, F.; Cox, P.; Neri, R.; Carilli, C.L.; Walter, F.; Omont, A.; Beelen, A.; Henkel, C.; Fan, X.; Strauss, M.A.; et al. High-excitation CO in a quasar host galaxy at z = 6.42. Astron. Astrophys. 2003, 409, L47, doi:10.1051/0004-6361:20031345.
- Mao, R.Q.; Henkel, C.; Schulz, A.; Zielinsky, M.; Mauersberger, R.; Stoerzer, H.; Wilson, T. L.; Gensheimer, P. Dense gas in nearby galaxies. XIII. CO submillimeter line emission from the starburst galaxy M 82 2000, Astronomy and Astrophysics, 358, 433.
- Beuther, H.; Schilke, P.; Wyrowski, F. High-spatial-resolution CN and CS observation of two regions of massive star formation. Astrophys. J. 2004, 615, 832.
- Yorke, H.W.; Sonnhalter, C. On the Formation of Massive Stars. ApJ, 2002, 569, 846.
- Kumar, M.S.N.; Fernandes, A.J.L.; Hunter, T.R.; Davis, C.J.; Kurtz, S. A massive disk/envelope in shocked H2 emission around an UCHII region.2003, Astronomy and Astrophysics, 412, 175.
- Gueth, F.; Bachiller, R.; Tafalla, M. Dust emission from young outflows: The case of L 1157 2003, Astronomy and Astrophysics, 401, L5.
- Hogerheijde, M.R.; Sandell, G. Testing Envelope Models of Young Stellar Objects with Submillimeter Continuum and Molecular-Line Observations. ApJ 2000, 534, 880.
- Porcas, R.W.; Alef, W.; Ghosh, T.; Salter, C.J.; Garrington, S.T. Compact structure in first survey sources. In Proceedings of 7th European VLBI Network Symposium on New Developments in VLBI Science and Technology and EVN Users Meeting, Toledo, Spain, 12–15 October 2004.
- Gras, S.; Fritschel, P.; Barsotti, L.; Evans, M. Resonant dampers for parametric instabilities in gravitational wave detectors. Phys. Rev. D 2015, 92, 082001.
- Hagood, N.; von Flotow, A. Damping of structural vibrations with piezo electric materials and passive electrical networks J. Sound Vib. 1991, 146, 243.
- Zhang, J.; Zhao, C.; Ju, L.; Blair, D. Study of parametric instability in gravitational wave detectors with silicon test masses. Class. Quant. Grav. 2017, 34, 055006.
- Tannirkulam, A.K.; Harries, T.J.; Monnier, J.D. The inner rim of YSO disks: Effects of dust grain evolution. Astrophys. J. 2007, 661, 374.
- Turyshev, S.G. Relativistic stellar aberration for the space interferometry mission (2). arXiv 2002, arXiv:gr-qc/0205062.
- Akeson, R.L.; Boden, A.F.; Monnier, J.D.; Millan-Gabet, R.; Beichman, C.; Beletic, J.; Hartmann, L.; Hillenbrand, L.; Koresko, C. ; Sargent, A.; et al. Keck interferometer observations of classical and weak line T tauri stars. Astrophys. J. 2005, 635, 1173, doi:10.1086/497436.
- Ding, F.; Croft, R.A.C. Future dark energy constraints from measurements of quasar parallax: Gaia, SIM and beyond. Mon. Not. R. Astron. Soc. 2009, 397, 1739, doi:10.1111/j.1365-2966.2009.15111.x.
- Papini, G. Zitterbewegung and gravitational Berry phase. Phys. Lett. A. 2012, 376, 1287.
- Winterflood, J.; Blair, D.G.; Notcutt, M.; Schilling, R. Position control system for suspended masses in laser interferometer gravitational wave detectors. Rev. Sci. Instrum. 1995, 66, 2763.
- Fujimoto, R. X-Ray Spectroscopic Observations of Intermediate Polars and Mass Determination of White Dwarfs. Ph.D. Thesis, (Tokyo U.) 1998.
- Hees, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Naoz, S.; Becklin, E.E.; Boehle, A.; Chappel, S.; Chu, D.; Dehghanfar, A.; et al. Testing General Relativity with stellar orbits around the supermassive black hole in our Galactic center. Phys. Rev. Lett. 2017, 118, 211101.
- Giacomelli, G. High-energy astrophysics: Status of observations at large underground detectors. In Proceedings of the 2nd International Workshop on Theoretical and Phenomenological Aspects of Underground Physics, Toledo, Spain, 9–13 September 1991.
- Giacomelli, G. High-energy underground physics and astrophysics. Nucl. Phys. (Proc. Suppl.) 1993, 33, 57–76.
- Beier, E.W.; Frank, E.D.; Frati, W.; Kim, S.B.; Mann, A.K.; Newcomer, F.M.; Van Berg, R.; Zhang, W.; Hirata, K.S.; Inoue, K.; et al. Survey of atmospheric neutrino data and implications for neutrino mass and mixing. Phys. Lett. B 1992, 283, 446.
- Parsons, A.R.; Backer, D.C. Calibration of low-frequency, wide-field radio interferometers using delay/delay-rate filtering. Astron. J. 2009, 138, 219, doi:10.1088/0004-6256/138/1/219.
- Bradley, R.; Backer, D.; Parsons, A.; Parashare, C.; Gugliucci, N.E. A. Precision Array to Probe the Epoch of Reionization In Bulletin of the American Astronomical Society; 2005 New York, N.Y. : American Institute of Physics USA.; p. 1216.
- Nozawa, I.; Gohdo, M.; Kan, K.; Kondoh, T.; Ogata, A.; Yang, J., Yoshida, Y. Bunch Length Measurement of Femtosecond Electron Beam by Monitoring Coherent Transition Radiation; JACoW: Geneva, Switzerland, 2015, doi:10.18429/JACoW-IPAC2015-MOPTY002.
- Frank, I.M.; Ginzburg, V.L. Radiation of a Uniformly Moving Electron Due to Its Transition from One Medium to Another.J. Phys.1945, 9, 353.
- Evans, L.; Bryant, P. LHC Machine; Journal of Instrumentation 3 (2008) S08001; 2008.; 164p.
- Aad, G.; Brad Abbott B.; Abdallah J.; Khalek S.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid O.; Abramowicz, H.; et al. Measurement of the tt production cross-section as a function of jet multiplicity and jet transverse momentum in 7 TeV proton-proton collisions with the ATLAS detector. JHEP 2015, 1501, 020.
- Antoniadis, I.; Dimopoulos, S.; Dvali, G.R. Millimeter range forces in superstring theories with weak scale compactification. Nucl. Phys. B 1998,516, 70.
- Price, J.C. International Symposium on Experimental Gravitational Physics; Michelson, P.F., Ed.; World Scientific: Singapore, 1988; pp. 436–439.
- Kapitulnik, A.; Kenny, T. NSF Proposal 1997, National Science Foundation, Alexandria, Virginia, USA.
- Weld, D.M.; Xia, J.; Cabrera, B.; Kapitulnik, A. A new apparatus for detecting micron-scale deviations from newtonian gravity. Phys. Rev. D. 2008, 77, 062006.
- Barnes, P.D., Jr.; Caldwell, D.; DaSilva, A. Low background underground facilities for the direct detection of dark matter. In Proceedings of the 1990 Summer Study on High Energy Physics, Snowmass, CO, USA, 25 June–13 July 1990.
- Gould, A. Cosmological density of WIMPs from solar and terrestrial annihilations. Astrophys. J. 1992, 388, 338–344.
