You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 2 by Lindsay Dong and Version 1 by Nozomu Suzuki.
When two or more surfactants are mixed, the critical micelle concentration and solubilization capability are changed, and a careful selection of the combination promotes the micelle formation and enhances the solubilizing capability. Thus, understanding the mechanism behind the phenomena is essential for controlling the physical properties of the mixed micelle. The interaction parameters β and B that describe the formation of mixed micelles and their partitioning of solutes, respectively, were proposed by Treiner four decades ago.
- surfactant
- mixed micelle
- regular solution theory
1. Introduction
Spherical micelles and vesicles can be applied to drug delivery, cancer therapy, and the pseudostationary phase for separation [1,2,3,4][1][2][3][4]. When two or more surfactants are mixed, the critical micelle concentration (CMC) and solubilization capability are changed, and a careful selection of the combination promotes the micelle formation and enhances the solubilizing capability [5,6,7,8,9][5][6][7][8][9]. Thus, understanding the mechanism behind the phenomena is essential for controlling the physical properties of the mixed micelle.
The micelle formation of the mixed micelle can be described by the regular solution theory [5[5][6],6], more appropriately called the simple mixture model, established by Rubingh and coworkers [10]. The theory uses the interaction parameter β for a binary mixture of surfactants. A negative value β means synergistic interaction, while a positive value indicates an antagonistic interaction. The CMC of the binary mixed micelle at an arbitrary composition can be appropriately described using the CMC of the pure surfactant and β [11].
An equation can also describe the partition coefficients of the mixed micelle based on the regular solution theory. O’Connell and Prausnitz originally derived the equation to calculate the solubility of inert gases in a binary solvent [12[12][13],13], and Treiner and coworkers applied the theory to the mixed micelle system with minor modifications [14,15,16][14][15][16]. The equations have been used for various mixed micelle systems [5,6,15,16,17,18,19,20,21,22,23,24][5][6][15][16][17][18][19][20][21][22][23][24].
Treiner and coworkers carefully categorized binary surfactants and solute systems and concluded a linear relation between the interaction parameters β and B when an appropriate combination of binary surfactants (nine examples) and polar solute was used [16,21][16][21]. The exceptions are nonpolar solutes, nonionic surfactants with long oxyethylene chains, and amphiphilic compounds such as yellow OB that undergo aggregation [21]. It has been four decades since Treiner reported the relation and many binary mixed micelle systems partitioning various solutes. In addition, there has been progress in modeling mixed micelle [10,25,26,27,28][10][25][26][27][28] and mixed solvent solubility [29,30][29][30]. These progresses may enforce the claim made by Treiner or help to develop a more general model that explains the relation between β and B.
2. Theories for the Formation and Partitioning of the Mixed Micelle
According to the regular solution theory, the CMC of the binary mixed micelle of surfactants 1 and 2 can be estimated using an interaction parameter (β) and the CMC of pure surfactants [5,6][5][6]. The parameter β is related to net (pairwise) interactions among surfactants 1 and 2 in the binary mixed micelle as β = N(W11 + W22 − 2W12)/RT, where N is Avogadro’s number, W11, W22, and W12 are the pairwise interaction energies between surfactants 1 and 2 in the micelles, R is the gas constant, and T is the temperature. If β > 0, then a repulsive (antagonistic) interaction is taking place between two surfactants, while β < 0 indicates an attractive (synergistic) interaction between the surfactants. The value of β = 0 indicates the ideal mixture of surfactants. Experimentally, only the mole fraction of total surfactant 1 (a1) and surfactant 2 (a2) are known, where a1 + a2 = 1 (see Figure 1).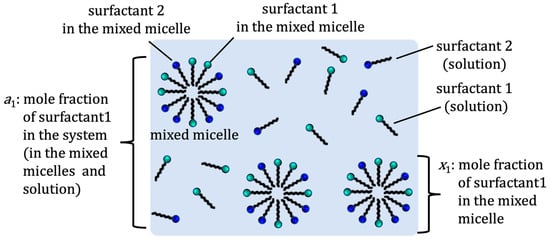
Figure 1.
Definition of mole fractions
a1
and
x1
.
The regular solution theory relates the mole fraction of surfactant 1 (x1) in the binary mixed micelle (Figure 1), the CMC of the pure surfactant 1 (C1) and binary mixed micelle (C12), and the mole fraction of surfactant 1 in total mixed surfactants (a1) as follows.
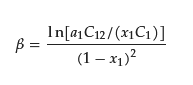
Since x1 is the mole fraction of surfactant in the binary mixed micelle 1, x2 = 1 − x1 holds. If C1, the CMC of the pure surfactant 2 (C2), C12, and a1 are known, the unknown variable x1 can be calculated by iteratively solving the following equation for x1.
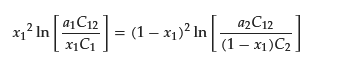
Experimentally, the x1 value is determined using ultrafiltration [31,32,33,34][31][32][33][34], small angle neutron scattering [35[35][36],36], or a combination of ion-selective electrodes and ultraviolet-visible absorption spectroscopy (UV–Vis) [37]. The theoretical x1 value obtained using the regular solution theory qualitatively agrees with the experiment [33,35][33][35]. According to the theory, x1 (= 1 − x2) at the CMC can be estimated by the following equation:
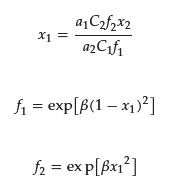
where f1 and f2 are activity coefficients of the surfactants 1 and 2, respectively.
The values of x1 and x2 (= 1 − x1) above the CMC can be calculated using the following equation:


where Ctotal is the total surfactant concentration. The concentration of surfactants 1 and 2 in the mixed micelles (C1,M and C2,M, respectively) with the CMC of C12 can be expressed as follows:


By defining synergism as “micelle formation at total mixed surfactant concentrations in the solution phase lower than the CMCs of both surfactants in the mixture”, Hua and Rosen derived the second condition for synergism (|ln(C1/C2)| < |β|) in addition to the first condition of β > 0 [38]. Likewise, they derived the second condition of antagonism as |ln(C1/C2)| < β in addition to the first criterion (β > 0).
O’Connell and Prausnitz derived the regular solution theory for Henry’s coefficient of the gas in the mixed solvent [12,13][12][13]. Treiner and coworkers applied the theory to the partition coefficients of the mixed micelle for solutes with slight modification as follows [14,15,20,21][14][15][20][21]:
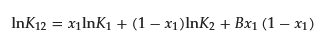
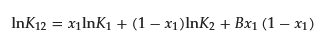
where K12, K1, and K2 are partition coefficients of a binary mixed micelle of surfactant composed of 1 and 2, pure micelle composed of surfactant 1, and that of surfactant 2, respectively. The value B is the interaction parameter and should be the same as β; however, they point out that assuming β = B is quantitatively not entirely satisfactory, even in the case of nonpolar gases in simple liquid mixtures, because of the omission of the contribution of the solute in the interaction parameter [15]. Therefore, they determined B separately from β, including all surfactant/surfactant and solute/surfactant interaction terms. Using the experimental data of the partition coefficient and CMC value, Treiner and colleagues proposed the following empirical equation to relate the values of β and B [16]:
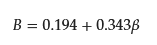
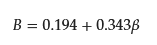
However, the meaning of B remained ambiguous. Recently, the author and coworkers proposed a relation [28].
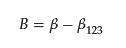
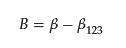
β123 is an additional interaction parameter involving the two surfactants (surfactant 1 and 2) and one solute (regarding the solute as the third component, surfactant 3, of the mixed micelle). The parameter can be determined by measuring the CMC of the ternary system (two surfactants and a solute), the method of which is presented in the reference [28]. The information gives the change in the interaction parameter specific to the ternary system. Still, the evaluation of parameter β123 requires evaluating the CMC in a ternary system and determining partitioning constants, treating one of the components as the solute. Such an example is limited so far [28], and further investigation is required to verify and find a relation between β123 and β.
Figure 2 summarizes the solute molecules used for determining the partition coefficients of the binary mixed micelles. Most of the solutes have a chromophore such as an aromatic ring. This could be because UV–Vis measurement is employed to evaluate the partition coefficient. In the case of UV–Vis measurement, the solute is the chromophore used in the spectroscopy assays. Since the relationship between B and β depends on the polarity of the solutes, the values of the octanol–water partition coefficient (logP) are estimated using ChemDraw 21.0.0.28.
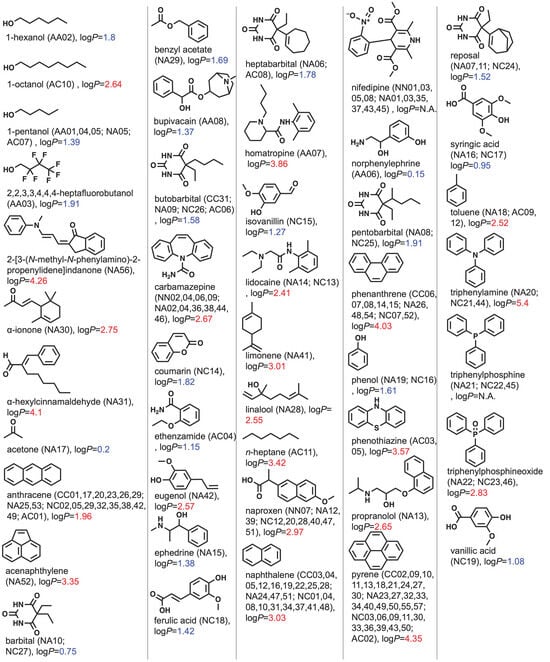

Figure 2. Chemical structures of solutes in alphabetical order. The system IDs are shown in parentheses. Values of logP were estimated using ChemDraw 21.0.0.28 and colored with blue if logP ≥ 1.96 (=logP of anthracene) and red if 1.96 > logP.
Figure 3, Figure 4, Figure 5 and Figure 6 show the chemical structures of surfactants used for studying the formation and partitioning of mixed micelles from the surfactants reported by researchers. The anionic surfactants include perfluoroalkyl surfactant LFOS, which shows an antagonistic interaction with surfactants bearing alkyl groups, resulting in a positive β value. For the Gemini surfactants [39] and bile salts [40], reviews on the interaction parameter β have recently been reported. Some compounds were excluded due to their undefined structure [41].
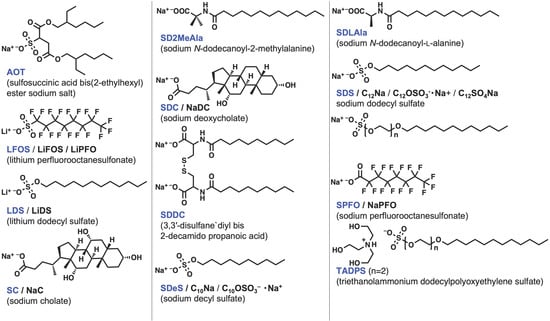

Figure 3. Chemical structures of anionic surfactants. The compound names used in this entry are colored in blue. The other abbreviations appear in the literature.
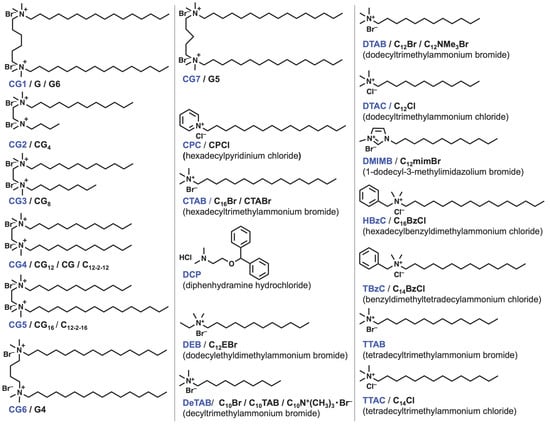

Figure 4. Chemical structures of cationic surfactants. The compound names used in this entry are colored in blue. The other abbreviations appear in the literature.
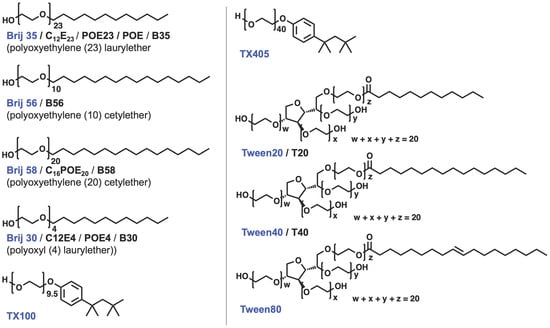

Figure 5. Chemical structures of nonionic surfactants. The compound names used in this entry are colored in blue. The other abbreviations appear in the literature.
Some studies of partitioning solutes using binary micelles did not provide information on the interaction parameter B. Such cases may require a further analysis based on their data or reproducing the experiment may be beneficial to note. In the literature, various methods were employed to analyze the micellar formation and partitioning of the solutes: surface tension (ST); fluorescence (FL); nuclear magnetic resonance (NMR); conductance (CD); gas chromatography (GC); UV–Vis; micellar enhanced ultrafiltration (MEUF); micellar liquid chromatography (MLC); high-performance liquid chromatography (HPLC); and micellar electrokinetic chromatography (MEKC). The most popular method to determine is ST, while the most popular method to determine B is UV–Vis measurement. MEKC was recently introduced and related to the regular solution theory to analyze the mixed micelle [27]. The method can determine not only the partition coefficients [42,43][42][43] but also the kinetics of the solute permeation of the micelles [44,45][44][45]. Various methods were used to analyze the interaction parameters, but comparative studies of the different methods to determine the interaction parameter for the partitioning of solutes using the same surfactants and solute combination have not been reported to the best of the author’s knowledge. The systems of the binary micelles are categorized with the types of composing surfactants: anionic/anionic (AA); cationic/cationic (CC); nonionic/nonionic (NN); nonionic/anionic (NA); nonionic/cationic (NC); and anionic/cationic (AC) surfactants. In general, the interaction between the two surfactants is mainly due to electrostatic forces, and the strength of the attractive electrostatic interaction parameter β decreases in the order of AN > NA ≈ NC > AA ≈ CC ≈ NN surfactants [11,27][11][27].
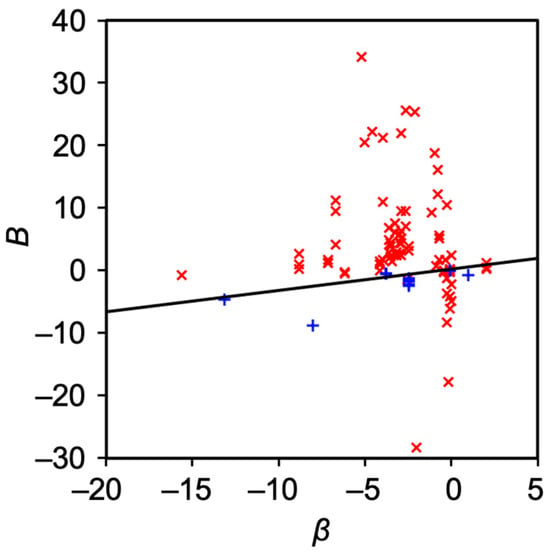

Figure 6. The relation between β and B. Red cross indicates nonpolar solute with logP > 1.96, while blue cross indicates polar solutes with 1.96 ≥ logP. The black line is drawn based on Equation (10).
References
- Molina, M.; Silva, M. Micellar Electrokinetic Chromatography: Current Developments and Future. Electrophoresis 2002, 23, 3907–3921.
- Ulbrich, K.; Holá, K.; Šubr, V.; Bakandritsos, A.; Tuček, J.; Zbořil, R. Targeted Drug Delivery with Polymers and Magnetic Nanoparticles: Covalent and Noncovalent Approaches, Release Control, and Clinical Studies. Chem. Rev. 2016, 116, 5338–5431.
- Li, Y.; Wang, Y.; Huang, G.; Gao, J. Cooperativity Principles in Self-Assembled Nanomedicine. Chem. Rev. 2018, 118, 5359–5391.
- Bernardo-Bermejo, S.; Sánchez-López, E.; Castro-Puyana, M.; Marina, M.L. Chiral Capillary Electrophoresis. Trends Anal. Chem. 2020, 124, 115807.
- Rubingh, D.N. Mixed Micelle Solutions. In Solution Chemistry of Surfactants; L. Mittal, K., Ed.; Springer: Boston, MA, USA, 1979; pp. 337–354.
- Holland, P.M.; Rubingh, D.N. Nonideal Multicomponent Mixed Micelle Model. J. Phys. Chem. 1983, 87, 1984–1990.
- Paria, S. Surfactant-Enhanced Remediation of Organic Contaminated Soil and Water. Adv. Colloid Interface Sci. 2008, 138, 24–58.
- Lamichhane, S.; Bal Krishna, K.C.; Sarukkalige, R. Surfactant-Enhanced Remediation of Polycyclic Aromatic Hydrocarbons: A Review. J. Environ. Manage. 2017, 199, 46–61.
- Schacht, V.J.; Grant, S.C.; Haftka, J.J.H.; Gaus, C.; Hawker, D.W. Transport potential of super-hydrophobic organic contaminants in anionic-nonionic surfactant mixture micelles. Chemosphere 2019, 230, 173–181.
- Slavchov, R.I.; Georgiev, G.S. Markov Chain Model for the Critical Micelle Concentration of Surfactant Mixtures. Colloid Polym. Sci. 2014, 292, 2927–2937.
- Rosen, M.J. Molecular Interactions and Synergism in Mixtures of Two Surfactants. In Surfactants and Interfacial Phenomena; Rosen, M.J., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 379–414.
- O’Connell, J.P.; Prausnitz, J.M. Thermodynamics of Gas Solubility in Mixed Solvents. Ind. Eng. Chem. 1964, 3, 347–351.
- O’Connell, J.P. Molecular Thermodynamics of Gases in Mixed Solvents. AIChE J. 1971, 17, 658–663.
- Treiner, C.; Bocquet, J.F.; Pommier, C. The Case of a Synergistic Solubilization Effect: The Partitioning of 1-Pentanol in Aqueous Solutions of Mixed Ionic Hydrocarbon and Fluorocarbon Surfactants. J. Phys. Chem. 1986, 90, 3052–3054.
- Treiner, C.; Nortz, M.; Vaution, C.; Puisieux, F. Micellar Solubilization in Aqueous Binary Surfactant Systems: Barbituric Acids in Mixed Anionic + Nonionic or Cationic + Nonionic Mixtures. J. Colloid Interface Sci. 1988, 125, 261–270.
- Treiner, C. The Thermodynamics of Micellar Solubilization of Neutral Solutes in Aqueous Binary Surfactant Systems. Chem. Soc. Rev. 1994, 23, 349–356.
- Zhu, B.Y.; Rosen, M.J. Synergism in binary mixtures of surfactants. J. Colloid Interface Sci. 1984, 99, 435–442.
- Treiner, C.; Vaution, C.; Miralles, E.; Puisieux, F. Influence of Sodium Dodecylsulfate and of Inorganic Electrolytes on the Micellar Solubilization of Butobarbitone in Aqueous Polyoxyethylene Lauryl Ether Solutions at 298.15 K. Colloids Surf. 1985, 14, 285–292.
- Asakawa, T.; Miyagishi, S.; Nishida, M. Fluorine Nuclear Magnetic Resonance of Fluorocarbon and Hydrocarbon Surfactant Mixtures. J. Colloid Interface Sci. 1985, 104, 279–281.
- Treiner, C.; Khodja, A.A.; Fromon, M. Micellar Solubilization of 1-Pentanol in Binary Surfactant Solutions: A Regular Solution Approach. Langmuir 1987, 3, 729–735.
- Treiner, C.; Nortz, M.; Vaution, C. Micellar Solubilization in Strongly Interacting Binary Surfactant Systems. Langmuir 1990, 6, 1211–1216.
- Sharma, K.S.; Patil, S.R.; Rakshit, A.K.; Glenn, K.; Doiron, M.; Palepu, R.M.; Hassan, P.A. Self-Aggregation of a Cationic−Nonionic Surfactant Mixture in Aqueous Media: Tensiometric, Conductometric, Sensity, Light Scattering, Potentiometric, and Fluorometric Studies. J. Phys. Chem. B 2004, 108, 12804–12812.
- Mir, M.A.; Chat, O.A.; Najar, M.H.; Younis, M.; Dar, A.A.; Rather, G.M. Solubilization of Triphenylamine, Triphenylphosphine, Triphenylphosphineoxide and Triphenylmethanol in Single and Binary Surfactant Systems. J. Colloid Interface Sci. 2011, 364, 163–169.
- Wei, J.; Huang, G.; An, C.; Yu, H. Investigation on the Solubilization of Polycyclic Aromatic Hydrocarbons in the Presence of Single and Mixed Gemini Surfactants. J. Hazard. Mater. 2011, 190, 840–847.
- Georgiev, G.S. Markov Chain Model of Mixed Surfactant Systems. Colloid Polym Sci. 1996, 274, 49–58.
- Suzuki, N. Understanding Nonlinear Composition Dependency of Enantioselectivity in Chiral Separation Using Mixed Micelle. J. Colloid Interface Sci. 2022, 627, 578–586.
- Suzuki, N. Regular Solution Theory for Nonlinear Composition Dependency of Enantioselectivity by Mixed Micelle. J. Mol. Liq. 2022, 367, 120597.
- Suzuki, N.; Taura, D.; Komichi, Y. Critical Micelle Concentration and Partition Coefficient of Mixed Micelles: Analysis of Ternary Systems Based on Markov Chain Model and Simple Mixture Model. J. Mol. Liq. 2023, 376, 121383.
- Jouyban, A. Review of the Cosolvency Models for Predicting Solubility of Drugs in Water-Cosolvent Mixtures. J. Pharm. Pharm. Sci. 2008, 11, 32–58.
- Jouyban, A. Review of the Cosolvency Models for Predicting Drug Solubility in Solvent Mixtures: An Update. J. Pharm. Pharm. Sci. 2019, 22, 466–485.
- Osborne-Lee, I.W.; Schechter, R.S.; Wade, W.H. Monomer—Micellar equilibrium of aqueous surfactant solutions by the use of ultrafiltration. J. Colloid Interface Sci. 1983, 94, 179–186.
- Warr, G.G.; Grieser, F.; Healy, T.W. Composition of mixed micelles of polydisperse nonionic surfactants. J. Phys. Chem. 1983, 87, 1220–1223.
- Makayssi, A.; Lemordant, D.; Treiner, C. Structural change and micellar composition in aqueous solutions of binary cationic surfactant mixtures as deduced from cross-flow ultrafiltration experiments. Langmuir 1993, 9, 2808–2813.
- Huang, L.; Somasundaran, P. Changes in Micelle Compositions and Monomer Concentrations in Mixed Surfactant Solutions. Langmuir 1996, 12, 5790–5795.
- Pedone, L.; Chillura Martino, D.; Caponetti, E.; Floriano, M.A.; Triolo, R. Determination of the Composition of Mixed Hydrogenated and Fluorinated Micelles by Small Angle Neutron Scattering. J. Phys. Chem. B 1997, 101, 9525–9531.
- Almgren, M.; Garamus, V.M.; Asakawa, T.; Jiang, N. Contrast Variation SANS Investigation of Composition Distributions in Mixed Surfactant Micelles. J. Phys. Chem. B 2007, 111, 7133–7141.
- Rodríguez, J.L.; Minardi, R.M.; Schulz, E.P.; Pieroni, O.; Schulz, P.C. The Composition of Mixed Micelles Formed by Dodecyl Trimethyl Ammonium Bromide and Benzethonium Chloride in Water. J. Surfactants Deterg. 2011, 15, 147–155.
- Hua, X.Y.; Rosen, M.J. Synergism in Binary Mixtures of Surfactants. J. Colloid Interface Sci. 1982, 90, 212–219.
- Naqvi, A.Z.; Kabir-ud-Din; Panda, M. Mixed micellization: Improved physicochemical behavior of different amphiphiles in presence of gemini surfactants. J. Mol. Liq. 2021, 343, 116876.
- Malik, N.A. Solubilization and Interaction Studies of Bile Salts with Surfactants and Drugs: A Review. Appl. Biochem. Biotechnol. 2016, 179, 179–201.
- Uchiyama, H.; Srivastava, A.; Fujimori, M.; Tomoo, K.; Nakanishi, A.; Tandia, M.; Kadota, K.; Tozuka, Y. Investigation of Physiological Properties of Transglycosylated Stevia with Cationic Surfactant and Its Application To Enhance the Solubility of Rebamipide. J. Phys. Chem. B 2018, 122, 10051–10061.
- Terabe, S. Capillary separation: Micellar electrokinetic chromatography. Annu. Rev. Anal. Chem. 2009, 2, 99–120.
- Rizvi, S.A.A.; Do, D.P.; Saleh, A.M. Fundamentals of micellar electrokinetic chromatography (MEKC). European Journal of Chemistry 2011, 2, 276–281.
- Miyabe, K.; Suzuki, N. Kinetic Study of Solute Permeation across Surfactant Micelle/Bulk Solvent Interface by Moment Analysis—Chromatographic Capillary Electrophoresis (MA-CCE). Bull. Chem. Soc. Jpn. 2016, 89, 1212–1218.
- Miyabe, K.; Inaba, S.; Umeda, M. A study on attempt for determination of permeation kinetics of coumarin at lipid bilayer of liposomes by using capillary electrophoresis with moment analysis theory. J. Chromatogr. A 2023, 1687, 463691.
More
