You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 1 by NADEEM HUSSAIN and Version 2 by Lindsay Dong.
Despite the recent initiatives and developments in building design provisions using performance-based design, practicing engineers frequently adopt force-based design approaches, irrespective of the structural system or building irregularity. Modern seismic building codes adopt the concept of simplifying the complex nonlinear response of a structure under seismic loading to an equivalent linear response through elastic analytical procedures using seismic design response factors. Nevertheless, code-recommended seismic design response factors may not result in a cost-effective design with a uniform margin of safety for different structural systems.
- multi-story buildings
- structural systems
- seismic response factors
- design codes
1. Introduction
Rapid urbanization in major metropolitan areas around the globe has witnessed scarcity and a high cost of land, giving rise to a remarkable increase in the number of multi-story building constructions. These multi-story buildings, if not acceptably designed, can be under significant threat from natural hazards that can cause potential damage to the structures, resulting in substantial economic losses. Lateral loads, particularly in wind- or earthquake-prone regions, usually govern the design of a multi-story building. Inelastic analysis is required to capture the seismic behavior realistically since buildings are expected to experience large deformations under the design of an earthquake. Practicing engineers adopt elastic analysis methods in the design of structures instead of nonlinear analysis, either due to economic reasons or a lack of required knowledge to utilize nonlinear analysis procedures. The inelastic response of a structure is accounted for in the elastic analysis methods by reducing seismic forces and amplifying deformations to arrive at safe designs with optimized costs. Thus, seismic design response factors play an essential part in the safety and economy of structures.
Seismic response factors prescribed in various design codes and guidelines covering different regions, structural systems, and constructional practices may not provide cost-effective designs for different structures and seismic zones with a uniform margin of safety [1][2][3][4][5][6][1,2,3,4,5,6]. Accurately calibrating these factors optimizes the seismic design forces, reducing costs for the overall structural system without compromising structural safety. This highlights the need for verifying the code-provided seismic design response factors of multi-story buildings with various structural systems using well-founded assessment methodologies.
2. Seismic Design Response Factors
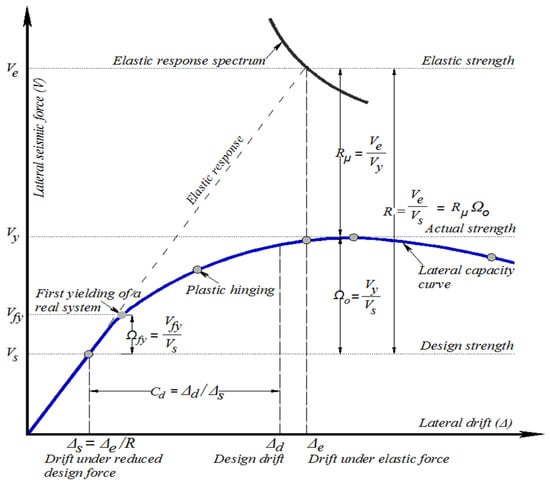
The seismic design forces of structures are derived in design codes by reducing the anticipated elastic seismic forces with a force reduction factor. The factors used to reduce seismic forces and amplify deformations to arrive at a safe design with optimized cost are termed seismic design response factors. Seismic design response factors may be based on engineering judgment and have a limited analytical basis [1]. The values of these seismic design factors adopted in seismic design codes do not provide uniform safety margins covering various structural systems, although they dictate the performance of buildings and the seismic design process. This presses the need for the proper selection of appropriate values of the seismic design factors for building structures, which has been a debatable issue in the development of seismic design provisions and highlighted in several previous studies. The shortcomings in seismic design factors are particularly evident at various performance levels and under bi-directional input ground motions [7][8][9][10][7,8,9,10]. Hence, the accurate evaluation of seismic design factors and the interrelationships between the different design parameters are essential components in the seismic design of multi-story buildings. The reserve strength and the ductility levels in a structure are utilized to reduce the seismic forces through the response modification factor [1][2][3][4][5][6][1,2,3,4,5,6]. Lateral load-resisting systems are designed to be deflection-controlled and possess adequate inelastic deformation capacity. The ductile detailing is essential to ensure that the components of these systems achieve a desirable behavior. Some previous studies highlighted the significance of redundancy in the structure to the seismic design response factors [11][12][13][14][11,12,13,14]. Figure 12 illustrates a typical lateral force–deformation relationship defining the components of seismic response factors, including the response modification factor (R), ductility reduction factor (Rμ), deflection amplification factor (Cd), and structural overstrength factor (Ωo), as recommended in various building codes [1][2][1,2]. The values of the R, Cd, and Ωo factors depend on the structural system and material.
Figure 12. Seismic design coefficients and their inter-relationship.
2.1. Historical Perspective of Seismic Response Factors
The evolution of seismic-resistant designed buildings can be traced several decades after the San Francisco earthquake of 1906 and classified into three phases [15][16]. The first phase adopted the application of the prescribed percentage of building weight as an applied load to the structure [17]. This was published under the first seismic code provisions of the Uniform Building Code (UBC) presented by SEAOC in 1927. The second phase used the concept of the seismic base shear (
Seismic design coefficients and their inter-relationship.
2.1. Historical Perspective of Seismic Response Factors
The evolution of seismic-resistant designed buildings can be traced several decades after the San Francisco earthquake of 1906 and classified into three phases [15,16]. The first phase adopted the application of the prescribed percentage of building weight as an applied load to the structure [17]. This was published under the first seismic code provisions of the Uniform Building Code (UBC) presented by SEAOC in 1927. The second phase used the concept of the seismic base shear (
V
) related to zone factor (
Z
), building system type (
K
), building period (
C
), and building weight (
W
) [18]. The response modification factor was introduced under this phase for the first time in the late 1970s to calculate the design base shear (
Vs
) of the structure by reducing the elastic base shear (
Ve
) with the reduction factor (
R
) using 5% damped acceleration for different systems. The present phase, also defined as the third phase, is based on applying the equivalent lateral force on the structure and employing spectral acceleration maps representing the site seismicity, importance factors, the natural building period, factors affecting the site, and the response modification factors [19].
2.2. Seismic Response Factors in Various Codes
Seismic design factors serve a similar function in all seismic design codes. These factors introduced in the seismic codes are denoted in different terms and assigned different numerical values. Brief comparisons of these factors practiced in various seismic codes are summarized in Table 1.Table 1.
Comparison of seismic design coefficients.
| Seismic Provisions | Applicable Region/ Country |
Response Modification Factor |
Deflection Amplification Factor |
Deflection Amplification Factor/ Response Modification Factor |
|---|---|---|---|---|
| ASCE 7-22 (2022) [20] | U.S. and other countries | R | Cd | 0.50–1.00 |
| Eurocode 8 (2004) [4] | Europe | q a | q | 1.00 c |
| NZS 1170.4 (2016) [21] | New Zealand | µ b | µ | 1.00 c |
| NBCC (2020) [22] | Canada | Rd/Ro | Rd/Ro | |
| MCBC (2015) [6] | Mexico | Q a | Q | 1.00 c |
| UBC | ||||
| UBC (1994) [23] | U.S. and other countries | Rw | (0.375)Rw | 0.375 |
| UBC (1997) [24] | R | 0.7R | 0.70 |
a reduces to 1.0 at T = 0 s and is period-dependent in the short period range. b does not reduce to 1.0 at T = 0 s and is period-dependent in the 0.45–0.7 s range. c greater than 1.0 in the short period range.
