Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Camila Xu and Version 1 by Boon Xian Chai.
Parallel computing, a significant portion of the problems faced by serial computing are gradually becoming obsolete. In both academic and industrial settings, the technique of parallel computing is often employed by researchers and industry practitioners alike to hasten the simulation-based optimisation processes.
- simulation
- computational cost
- optimisation
- composite
- liquid composite moulding
1. Introduction
Currently, large-scale composite manufacturing is commonly achieved via liquid composite moulding processes [1,2,3,4][1][2][3][4]. The utilisation of numerical process simulation has greatly facilitated the challenging task of LCM process optimisation, providing ease of solution evaluation at a significantly reduced cost compared to complete reliance on physical prototyping. Nevertheless, the computational cost of performing such composite moulding simulations is still considerably expensive at present, given its complexity [5,6,7][5][6][7]. As a consequence, the overall computational cost of simulation-based optimisation can be enormous, as each solution evaluation is essentially a numerical simulation run that typically requires a long computing time. In fact, within the setting of simulation-based optimisation, the cost of computing the process simulation accounts for a major portion of the total optimisation cost associated. Full-scale numerical simulation of the mould-filling process can become progressively cost-prohibitive to compute as the number of optimisation iterations required increases. Moreover, as more sophisticated and accurate multi-scale coupled textile-flow models are progressively being developed, the cost of simulation will further increase in the future, likely by a significant margin compared to contemporary meso-scale Darcy’s-Law-based flow models [6,8,9][6][8][9]. Therefore, the high cost of process simulation, in terms of both the computational power and computation time required, needs to be addressed promptly as the key bottleneck to the application of simulation-based optimisation. Principally, the high cost of simulation-based optimisation can be effectively addressed by either: (i) reducing the total number of solution evaluations required during the optimisation process, and/or, (ii) reducing the computational cost of the process simulation [7,10,11,12][7][10][11][12].
As highlighted in [6[6][8],8], the felicitous selection of optimisation algorithms with respect to the problem context (i.e., mould-filling scenario) can greatly reduce the number of solution evaluations required during the optimisation process. Aside from the appropriate selection of optimisation algorithms, how one can effectively utilise problem-specific knowledge and information to streamline the optimisation framework also receives massive attention in the research community [13]. The inclusion and exploitation of known problem structures and characteristics, process constraints, and insights of the mould-filling process during algorithm development and implementation can significantly lessen the resultant optimisation cost.
2. Parallel Computing
In the recent past, computer algorithms have conventionally been developed for serial computing [14,15,16,17][14][15][16][17]. Consequently, when solving a problem, only a single task (or instruction) is executed at any moment in time. As a result, there is an inefficient utilisation of the hardware resources available, where only a part of the potential computing capability is employed at any particular instance. Nowadays, these superannuated approaches to algorithm design are being progressively phased out as developments in parallel hardware architecture progress steadily [14,17,18][14][17][18]. Thanks to the rapid advancements in the field of parallel computing, a significant portion of the problems faced by serial computing are gradually becoming obsolete. In both academic and industrial settings, the technique of parallel computing is often employed by researchers and industry practitioners alike to hasten the simulation-based optimisation processes [7,10,19,20][7][10][19][20]. The streamlining of the simulation-based optimisation process via parallel computing for LCM process optimisation is no exception [7,20,21][7][20][21]. Parallel computing can be understood as the act of breaking down a larger, complex problem into numerous smaller, independent sub-tasks and computing them simultaneously across multiple processing units. The individual outputs of these parallel sub-tasks can then be remerged, upon their completion, back into the original problem framework for completion or further analysis. The schematic framework of parallel computing is depicted in Figure 1.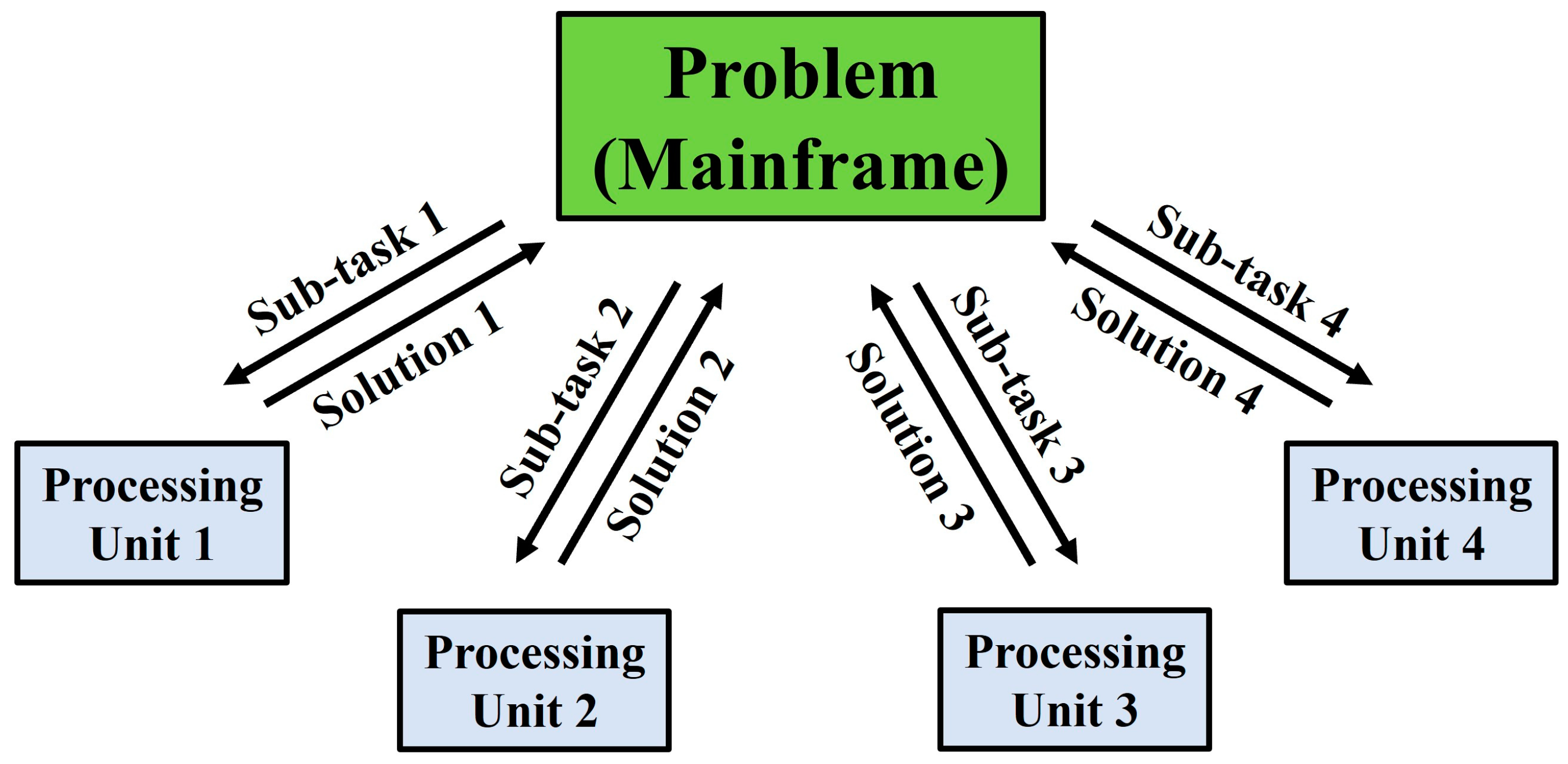
Figure 1.
The schematic framework of the application of parallel computing to solve a problem.
 where N can be either:
where N can be either:
- (i)
-
the number of processing units, or
- (ii)
-
the size of the problem, depending on the hardware’s parallel architecture. Note, only a minor proportion of all contemporary algorithms can be decomposed into completely independent pieces, enabling the theoretical linear speedup.By performing the independent solution evaluations simultaneously, the search process of the population-based optimisation algorithms can be expedited significantly. Do note, the maximum performance improvement achievable is limited by the fraction of parallelisable components within the population-based optimisation algorithms. The theoretical speedup 𝑆𝑇𝐻𝐸𝑂𝑅𝐸𝑇𝐼𝐶𝐴𝐿 for the population-based algorithms by parallel computing can be expressed by the Amdahl’s law [14,15[14][15][17][22],17,22], as:
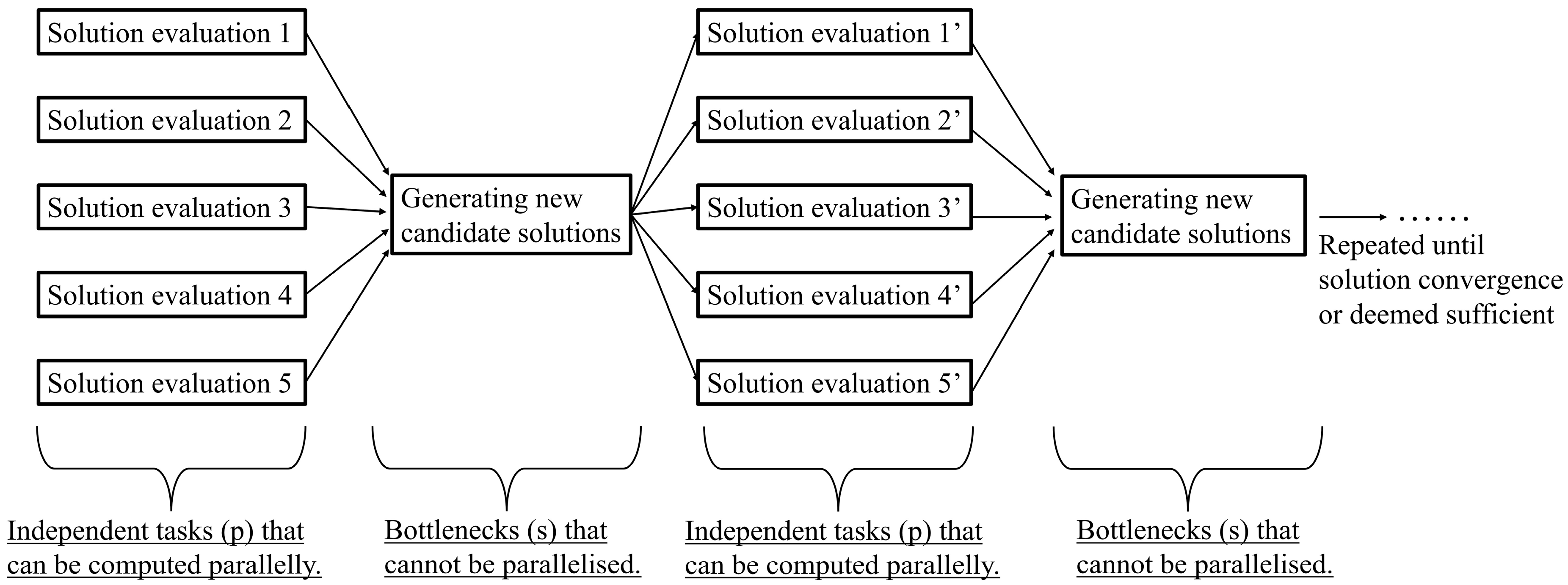 Figure 2.The generic search flow diagram of population-based optimisation algorithms.
Figure 2.The generic search flow diagram of population-based optimisation algorithms. where P is the fraction of the independent tasks within the algorithm that can be executed parallelly (e.g., evaluating the individuals within each generation of GA) and N is the number of processing units utilised.
Parallel computing can also be adopted to minimise the computational cost of the statistical modelling and characterisation for LCM processes via the Monte Carlo simulation approach [8,14,22][8][14][22]. These statistical analyses are critical to combat the issues of process randomness and lack of process repeatability within the LCM processes [8,26][8][26]. Parallel computing allows the user to perform the parallel computation of stochastic simulations for statistical modelling purposes and to perform parallel replications of a stochastic simulation for statistical characterisation purposes. Minimising the computational cost of these stochastic simulations will aid in securing the process robustness of the mould-filling stage [7,8,27][7][8][27]. Additionally, parallel computing can also be extremely valuable for the development and training of metamodels as the metamodel training data required are generally independent of one another, allowing parallelism [7,8,14][7][8][14].
While there are many levels of parallelism attainable, not every optimisation algorithm can exploit the merits of parallel computing in the setting of simulation-based optimisation. The adoption of certain algorithm structures, which is often dictated by the nature of the problem itself, may prohibit the simultaneous execution of computing tasks and prevent effective parallelisation [8,14,17,24][8][14][17][24]. Moreover, the issue of flow dependency is also pertinent to the adoption of parallel computing in simulation-based optimisation. Flow dependency, also commonly known as read-after-write (RAW), refers to the scenario where the execution of a task is dependent on the output of its preceding task [14,15,17,24][14][15][17][24]. As such, parallel computing is practically ineffectual for single-solution serial optimisation algorithms that: (i) evaluate only a single candidate solution during each evaluation iteration; and (ii) require knowledge of prior solution evaluation(s) to guide the following search phase (i.e., the exploration/search mechanism). For this type of algorithm, as each search phase is dependent on the result of its prior solution evaluation(s), the upcoming search tasks are forced to remain on hold until the prior solution evaluation is completed, preventing the effective distribution of computational workload. The generic search flow diagram of single-solution serial algorithms is depicted in Figure 3.
In summary, while the adoption of parallel computing has great potential in the application of simulation-based optimisation, its efficacy and applicability are highly dependent on the degree of achievable parallelism imposed by the algorithm’s framework and its flow dependencies [8,14,17,21][8][14][17][21]. Besides that, the application of parallel computing requires the development and execution of additional auxiliary algorithms to parallelise the existing optimisation framework (e.g., for task partitioning, task scheduling, task synchronisation, etc.) [14,17,19,22][14][17][19][22]. Lastly, the framework of parallel computing can be challenging to construct and implement. The complex operations of data transfer, memory organisation, communication, and synchronisation between multiple (locally or non-locally) independent processing units may require a significant effort to maintain smoothly [14,15,16,17][14][15][16][17]. In particular, issues arising from network latency and the non-homogeneity in computational power across the independent processing units can greatly complicate the vital tasks of communication and synchronisation during parallel computing. The overhead cost of these control operations can also be a deterrent to the adoption of parallel computing, as these fundamental operations can be computationally demanding to execute as well [14,16,17,19][14][16][17][19]. A delicate trade-off between the additional computational cost required versus the computational time saved is thus essential for the effective application of parallel computing in simulation-based optimisation settings.
where P is the fraction of the independent tasks within the algorithm that can be executed parallelly (e.g., evaluating the individuals within each generation of GA) and N is the number of processing units utilised.
Parallel computing can also be adopted to minimise the computational cost of the statistical modelling and characterisation for LCM processes via the Monte Carlo simulation approach [8,14,22][8][14][22]. These statistical analyses are critical to combat the issues of process randomness and lack of process repeatability within the LCM processes [8,26][8][26]. Parallel computing allows the user to perform the parallel computation of stochastic simulations for statistical modelling purposes and to perform parallel replications of a stochastic simulation for statistical characterisation purposes. Minimising the computational cost of these stochastic simulations will aid in securing the process robustness of the mould-filling stage [7,8,27][7][8][27]. Additionally, parallel computing can also be extremely valuable for the development and training of metamodels as the metamodel training data required are generally independent of one another, allowing parallelism [7,8,14][7][8][14].
While there are many levels of parallelism attainable, not every optimisation algorithm can exploit the merits of parallel computing in the setting of simulation-based optimisation. The adoption of certain algorithm structures, which is often dictated by the nature of the problem itself, may prohibit the simultaneous execution of computing tasks and prevent effective parallelisation [8,14,17,24][8][14][17][24]. Moreover, the issue of flow dependency is also pertinent to the adoption of parallel computing in simulation-based optimisation. Flow dependency, also commonly known as read-after-write (RAW), refers to the scenario where the execution of a task is dependent on the output of its preceding task [14,15,17,24][14][15][17][24]. As such, parallel computing is practically ineffectual for single-solution serial optimisation algorithms that: (i) evaluate only a single candidate solution during each evaluation iteration; and (ii) require knowledge of prior solution evaluation(s) to guide the following search phase (i.e., the exploration/search mechanism). For this type of algorithm, as each search phase is dependent on the result of its prior solution evaluation(s), the upcoming search tasks are forced to remain on hold until the prior solution evaluation is completed, preventing the effective distribution of computational workload. The generic search flow diagram of single-solution serial algorithms is depicted in Figure 3.
In summary, while the adoption of parallel computing has great potential in the application of simulation-based optimisation, its efficacy and applicability are highly dependent on the degree of achievable parallelism imposed by the algorithm’s framework and its flow dependencies [8,14,17,21][8][14][17][21]. Besides that, the application of parallel computing requires the development and execution of additional auxiliary algorithms to parallelise the existing optimisation framework (e.g., for task partitioning, task scheduling, task synchronisation, etc.) [14,17,19,22][14][17][19][22]. Lastly, the framework of parallel computing can be challenging to construct and implement. The complex operations of data transfer, memory organisation, communication, and synchronisation between multiple (locally or non-locally) independent processing units may require a significant effort to maintain smoothly [14,15,16,17][14][15][16][17]. In particular, issues arising from network latency and the non-homogeneity in computational power across the independent processing units can greatly complicate the vital tasks of communication and synchronisation during parallel computing. The overhead cost of these control operations can also be a deterrent to the adoption of parallel computing, as these fundamental operations can be computationally demanding to execute as well [14,16,17,19][14][16][17][19]. A delicate trade-off between the additional computational cost required versus the computational time saved is thus essential for the effective application of parallel computing in simulation-based optimisation settings. Figure 3.The generic search flow diagram of single-solution serial algorithms.
Figure 3.The generic search flow diagram of single-solution serial algorithms.
References
- Blythe, A.; Fox, B.; Nikzad, M.; Eisenbart, B.; Chai, B.X. Stiffness Degradation under Cyclic Loading Using Three-Point Bending of Hybridised Carbon/Glass Fibres with a Polyamide 6,6 Nanofibre Interlayer. J. Compos. Sci. 2022, 6, 270.
- Blythe, A.; Fox, B.; Nikzad, M.; Eisenbart, B.; Chai, B.X.; Blanchard, P.; Dahl, J. Evaluation of the Failure Mechanism in Polyamide Nanofibre Veil Toughened Hybrid Carbon/Glass Fibre Composites. Materials 2022, 15, 8877.
- Yu, C.; Song, Y.S. Enhancing energy harvesting efficiency of form stable phase change materials by decreasing surface roughness. J. Energy Storage 2023, 58, 106360.
- Capricho, J.C.; Liao, T.; Chai, B.X.; Al-Qatatsheh, A.; Vongsvivut, J.; Kingshott, P.; Juodkazis, S.; Fox, B.L.; Hameed, N. Magnetically Cured Macroradical Epoxy as Antimicrobial Coating. Chem. Asian J. 2023, 18, e202300237.
- Chai, B.X.; Eisenbart, B.; Nikzad, M.; Fox, B.; Blythe, A.; Bwar, K.H.; Wang, J.; Du, Y.; Shevtsov, S. Application of KNN and ANN Metamodeling for RTM Filling Process Prediction. Materials 2023, 16, 6115.
- Chai, B.X.; Eisenbart, B.; Nikzad, M.; Fox, B.; Blythe, A.; Blanchard, P.; Dahl, J. A novel heuristic optimisation framework for radial injection configuration for the resin transfer moulding process. Compos. Part A Appl. Sci. Manuf. 2023, 165, 107352.
- Achim, V.; Ruiz, E. Guiding selection for reduced process development time in RTM. Int. J. Mater. Form. 2010, 3, 1277–1286.
- Chai, B.X.; Eisenbart, B.; Nikzad, M.; Fox, B.; Blythe, A.; Blanchard, P.; Dahl, J. Simulation-based optimisation for injection configuration design of liquid composite moulding processes: A review. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106540.
- Shevtsov, S.; Zhilyaev, I.; Chang, S.H.; Snezhina, N.; Chai, B.X. Modeling Post-Infusion Application of Controlled External Pressure to a Polymer Composite Part. Int. J. Eng. Res. Mech. Civ. Eng. (IJERMCE) 2023, 10, 29–37.
- Tekin, E.; Sabuncuoglu, I. Simulation optimization: A comprehensive review on theory and applications. IIE Trans. 2004, 36, 1067–1081.
- Aguado, J.V.; Borzacchiello, D.; Ghnatios, C.; Lebel, F.; Upadhyay, R.; Binetruy, C.; Chinesta, F. A Simulation App based on reduced order modeling for manufacturing optimization of composite outlet guide vanes. Adv. Model. Simul. Eng. Sci. 2017, 4, 1.
- Park, C.H.; Saouab, A.; Bréard, J.; Riche, R.L. Simple models for mold filling stage in liquid composite molding and their applications to structure-process coupled optimization. In Proceedings of the 8th International Conference on Flow Processes in Composite Materials (FPCM8), Douai, France, 11–13 July 2006; pp. 289–296.
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82.
- Censor, Y.; Zenios, S. Parallel Optimization: Theory, Algorithms, and Applications; Oxford University Press: Oxford, UK, 1997.
- Fu, M.C. Handbook of Simulation Optimization; Springer: New York, NY, USA, 2014.
- Rensink, A.; Cuadrado, J.S. Theory and Practice of Model Transformation. In Proceedings of the 11th International Conference (ICMT 2018), Toulouse, France, 25–26 June 2018.
- Trobec, R.; Vajteršic, M.; Zinterhof, P. Parallel Computing: Numerics, Applications, and Trends; Springer Verlag London Limited: London, UK, 2009.
- Ho, Y.C. An explanation of ordinal optimization: Soft computing for hard problems. Inf. Sci. 1999, 113, 169–192.
- Fu, M.C. Optimization for simulation: Theory vs Practice. INFORMS J. Comput. 2002, 14, 192–215.
- Chebil, N.; Deléglise-Lagardère, M.; Park, C.H. Efficient numerical simulation method for three dimensional resin flow in laminated preform during liquid composite molding processes. Compos. Part A Appl. Sci. Manuf. 2019, 125, 105519.
- Liu, J.; Xie, J.; Chen, L. A hybrid optimization algorithm for gate locations in the liquid composite molding process. Text. Res. J. 2022, 1, 1–9.
- Hussein, M.; Eltoukhy, A.E.E.; Darko, A.; Eltawil, A. Simulation-Optimization for the Planning of Off-Site Construction Projects: A Comparative Study of Recent Swarm Intelligence Metaheuristics. Sustainability 2021, 13, 13551.
- Lin, M.Y.; Murphy, M.J.; Hahn, H.T. Resin transfer molding process optimization. Compos. Part A Appl. Sci. Manuf. 2000, 31, 361–371.
- Spall, J.C. Introduction to Stochastic Search and Optimization; Wiley-Interscience: Hoboken, NJ, USA, 2005.
- Šimáček, P.; Advani, S.G. Desirable features in mold filling simulations for Liquid Composite Molding processes. Polym. Compos. 2004, 25, 355–367.
- Gokce, A.; Advani, S.G. Vent location optimization using Map-Based Exhaustive Search in Liquid Composite Molding processes. Mater. Manuf. Process. 2004, 19, 523–548.
- Li, J.; Zhang, C.; Liang, R.; Wang, B. Robust design of composites manufacturing processes with process simulation and optimisation methods. Int. J. Prod. Res. 2008, 46, 2087–2104.
More
