Performance of Unreinforced Masonry Walls in Compression

Performance of Unreinforced Masonry Walls in Compression: Comparison

Please note this is a comparison between Version 3 by Sirius Huang and Version 2 by Sirius Huang.

Unreinforced masonry (URM) is a construction of brick or concrete block unit that is joined together using mortar, without steel reinforcement. Because of the heterogeneous nature and difference in mechanical properties of the masonry elements, analyzing and capturing the structural behaviour of URM walls under various loading conditions is therefore complex.

compressive strength
elastic modulus
masonry wall
masonry design standards
stress–strain relation
unreinforced masonry

1. Introduction

A masonry wall is the structural assemblage of masonry elements, i.e., bricks or blocks with mortar as the binding material. Masonry walls and the building as a whole are designed to be durable, stable, and resilient under sustained loading. In masonry construction, the imposed loads are supported and transmitted to the foundations by the bricks or blocks joined together by mortar and, in some cases, are filled with grouts and reinforcements. One significant benefit of masonry building—aside from the ease of construction with readily available basic materials—is the durability of masonry materials such as the unit, which, with proper selection, could be expected to last for several decades, if not centuries, with very little maintenance ^[1]. Despite the ease with which masonry buildings are constructed, the analysis of its structural behaviour still remains a difficult challenge.

Unreinforced Masonry (URM) walls are largely non-homogeneous, non-elastic, and anisotropic elements made up of two materials with very different characteristics—one element of either mortar or unit considerably stiffer than the other—and a relatively weak bond between them ^[2][3][4]. Thus, masonry walls are relatively weak in tension. As a result, the walls are usually designed and expected to resist only compression loads ^[5][6][7][8]. Over the last several decades, research studies have been dedicated to investigating the structural behaviour of masonry walls and improving design standards ^[9][10][11]. In particular, significant attention has been focused on masonry components and the interaction between them. The walls of a structural masonry building serve as the primary resisting component against dynamic or static loads exerted on the structure, and as such, its compressive strength is of utmost importance when designing masonry walls in different loading conditions. In addition, the compression behaviour of masonry walls is a key factor in the design of masonry structures for other actions, such as in-plane shear and out-of-plane flexural behaviour ^[12]. However, the analysis of masonry walls under axial compressive load has been largely overlooked in the past.

In recent years, several research studies have been dedicated to investigating the axial compressive behaviour of URM walls ^{[13][14][15][16][17][18][19][20][21][22][23]}. In general, the mechanical properties of each masonry element and bonding properties between mortar and units are of major significance in the compressive behaviour of URM walls as a composite material. As a result, the behaviour of axially loaded URM walls becomes very complicated because it is dependent on several factors relating to the slenderness ratio and eccentric loading conditions of the walls. Moreover, multiple provisions in the masonry design standards are stipulated in predicting the strength of URM walls under axial compressive loading ^[24][25][26]. Nonetheless, there are discrepancies observed in existing design standards to predict the compressive strength of URM wall structures, particularly in the guidelines in choosing and testing of wall configurations.

2. Masonry Units in Construction

Masonry wall units such as blocks or bricks are primarily made of concrete, calcium silicate, and clay. Blocks and bricks come in a variety of forms, shapes and sizes, including solid, hollow, and interlocking (e.g., see a selection in Figure 1). All these units have roughly comparable functionalities, but their properties vary markedly and are dependent on their constituent raw materials employed and their mode of production. Besides solid block and brick units, hollow concrete blocks (HCB) are widely attractive nowadays in low- and medium-rise constructions due to their advantages like light weight, ease of construction, and higher load-bearing capacity, as well as their ability to facilitate conduits for concealing electrical units, sewer, and water pipes ^[9][27][28]. Under similar conditions, the quantity of masonry mortar used to lay HCB can be lowered by more than 50% when compared to solid concrete blocks, thereby significantly lowering construction costs.

Figure 1. Construction method of unreinforced masonry: (a) hollow clay bricks, (b) interlocking clay brick, and (c) hollow concrete block masonry.

With regard to masonry unit characteristics, its compressive strength is the most important. In addition to being closely associated with the strength of the wall, the properties of the unit provide an overall indicator of the masonry characteristics ^[29]. It is evaluated using standardized tests, and the results rely largely on the conditions and recommendations specified in the relevant standards in use. It can be said that the axial compression behaviour of masonry blockwork differs considerably from brick masonry since not only does the mortar strength influence the axial compression response but also the type and shape of block unit and strength of grout can inadvertently influence the overall response of the masonry wall ^[6][28][30]. Clay bricks can be made with compressive strength as high as 100 N/mm², but modest strength, i.e., 20–40 N/mm², is usually adequate for low-rise residential construction and the cladding of walls in medium-rise constructions. Concrete block units have lesser normalized strength, which ranges between 2.8 and 35 N/mm², but the effect mentioned previously must be considered if comparisons are to be made. In addition, the strength of brickwork will be lower than that of the corresponding blockwork if made from clay units with a similar strength value ^[31]. Although mortar represents only about 7% of total masonry volume, it has a far greater impact on performance than this fraction suggests. Conventional mortar mixtures are composed of cement, sand, plasticizer, or lime, and the mortar mix is graded based on its compressive strength ^[32]. The stiffer the mixture, the less it can facilitate movement, and thus, it is not recommended to employ a stronger mixture than required to satisfy performance requirements ^[31]. Various types of concrete blocks are also available, such as aerated autoclaved concrete (AAC) ^[33][34], whose material density ranges from 450 to 850 kg/m³ and enables the sizeable solid unit to be handled without mechanical support. The use of core-aligned blocks with special geometries, such as the Double H block ^[35], interlocking bricks ^{[36][37][38][39][40]}, cellular lightweight concrete (CLC) ^[41][42][43], and three-cell concrete block ^[44], have also garnered a lot of attention in recent years. The development of these newer types of blocks necessitates corresponding research into the adequacy and durability of such blocks for continued usage in masonry construction, and in particular to walls subjected to compressive loads.

3. Overview of Experimental Research in the Literature

As previously stated, various construction and testing parameters can influence the compressive performance of URM walls. The primary factors are the strength of masonry units (brick/block) and mortar strength, as well as the slenderness ratio and eccentric load conditions of the walls ^[17]. Apart from these parameters, the presence of openings is another significant parameter which could affect the performance of the masonry structure and should be properly taken into account. All the above-mentioned parameters can be varied during the construction and testing of masonry walls, leading to a more accurate assessment of the design of load-carrying URM elements. When evaluating the structural response of URM walls, both shear capacity and bending moment should be considered by taking into account its interaction with compression forces due to lateral load and gravity ^[45][46][47]. In the context of masonry structures in general, substantial eccentricity loadings could be precipitated either by in-plane or out-of-plane lateral forces or a combination of both ^[48]. The latter are typically induced by thrusting components (e.g., vaults and arches), wind and soil pressures and seismic actions transmitted from the masonry floor. In contrast, the former can be seismic-induced shear force ensuing from box-type global seismicity of the building structures. As observed from the literature (e.g., see ref. ^[49]), axial loading differs from eccentrically loaded walls since the former is a statically determinate problem in which the strength of a given wall panel may be presumed to be maximum compression forces divided by the total cross section (Figure 2). On the contrary, eccentrically loaded wall panels are statically indeterminate problems in which the bending moment could be defined by integrating the normal stress and the corresponding axial strain over the given gross sectional area ^[50][51][52]. As a general recommendation in the design of URM structures, the capacity reduction factor (Φ)—expressed as a ratio of prism strength to the strength of the wall—can be introduced to accommodate and account for different characteristics and to obtain the permissible compressive strength of the masonry ^[24][53][54].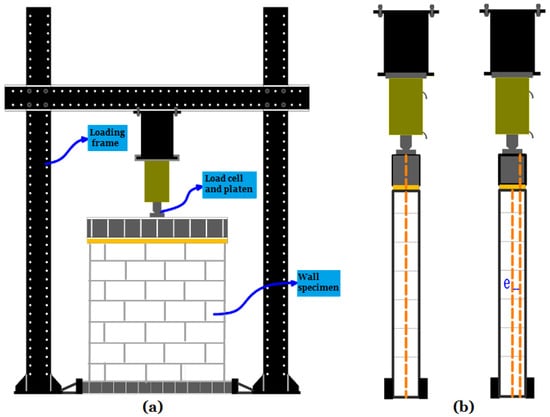

Figure 2. Axial compressive test of URM wall: (a) wall with test frame and (b) concentric and eccentric loading.

In evaluating the axial compressive performance of URM walls, experimental tests carried out on brick and concrete block masonry wall specimens available in the literature have been analyzed (e.g., see a selection in Table 1). However, it is important to highlight that previous research on the compressive behaviour of full-scale masonry walls is still limited. To augment the understanding, tests conducted on wallettes and partially grouted wall panels subjected to axial compressive loading have been used since the actual behaviour of these types of wall panels is identical to full-scale URM wall panels ^[12]. In addition, URM wall panels subjected to shear–compression loading have also been examined. However, the results from such experiments reported in the literature were not included in the database since these types of tests are closely associated with earthquake loadings. Based on a series of assumptions, scholars have introduced a wide range of predictive models to estimate the compressive strength of masonry. These models vary from simple linear ones with a single variable to complex nonlinear ones that consider the influence of multiple variables. Linear models were proposed in ^[55][56], while nonlinear expressions were introduced via standards such as Eurocode 6 ^[24]. These expressions established correlations between the compressive strength of masonry and both the compressive strength of the unit and the compressive strength of mortar. In many cases, the expressions proposed did not consider any distinctions based on the type of masonry. However, beyond the compressive strength of masonry constituents, additional factors were considered by researchers like Khan et al. ^[57]. The authors introduced a mathematical model that takes into account the slenderness ratio (height-to-thickness ratio, h/t) and the width-to-thickness ratio (l/t). A summary of the expressions proposed in the literature for calculating the compressive strength of masonry wallettes is provided in Table 2. The fotabllowing sectionses below present a review of the literature on the compressive performance of URM walls, summarizing the work and salient observations made by earlier researchers in different experimental campaigns. Code provisions have also been compared with results from experimental studies, and disparities are highlighted to identify and outline potential directions for future studies.

Table 1. Overview of experimental studies on compressive tests of unreinforced masonry.

Reference	Year of Publication	Unit Type	Material	Wall Dimensions	No. of Samples	Properties of Masonry Elements (MPa)			Test Parameter
Reference	Year of Publication	Unit Type	Material	H × L × T (mm)	No. of Samples	f_b	f_m	f_g	Test Parameter
Camacho et al. ^[13]	2015	HCB	Conv. concrete	1000 × 900 × 140	9	8.64; 15.76	7	17	Axial load; stress–strain.
Fortes et al. ^[14]	2017	HCB	High-strength concrete	2200 × 1200 × 140, 2200 × 800 × 140	30	18.7–34.5	13.4–26.9	31.3–42.4	Axial load; stress–strain.
Keshava and Raghunath ^[16]	2017	Brick SCB HCB	Table moulded; Conv. Concrete; Conv. Concrete.	2500 × 950 × 220; 2560 × 1030 × 150; 2600 × 830 × 150	14	5.8 4.5 6.0
3.8–15.8

6.5; 7.9
6.4; 3.9
–
Axial load; stress–strain.

Note: HCB = hollow concrete block, SCB = solid concrete block, CCB = cellular concrete block, CS = calcium silicate, AAC = autoclaved aerated concrete, Conv. = conventional, f_b = compressive strength of unit, f_m = compressive strength of mortar, f_g = compressive strength of grout.

Table 2. A summary of selected equations proposed in the literature for predicting either the characteristic compressive strength of the masonry, f_k, or the mean value, f’_m, using the normalized compressive strength of the unit, f_b, and the compressive strength of the mortar, f_m.

Reference	Masonry Type	Model
Eurocode 6 ^[24]	Clay and calcium silicate units	f’_k = 0.55 f_b ^0.70 f_m ^0.3
Gumaste et al. ^[15]	Calibrated for table moulded brick masonry	f’_m = 0.317 f_b ^0.866 f_m ^0.134
9.4	–	Axial load; slenderness ratio and eccentricity.
Khan et al. ^[57]	Calibrated for clay brick wallette	f’_m $= f_{b} (\frac{4 + 0.1 f m}{1.5 l / t + 5 h / t})$	Amalkar et al. ^[17]	2020
Hendry and Malek ^[58]	CCB	HCB	Conv. Concrete; Conv. Concrete.	2667 × 802 × 200; 2680 × 800 × 200, 2680 × 830 × 150	9	7.1 13.7; 6.6	5.3	–	Axial load; slenderness ratio and eccentricity.
Calibrated for clay brick masonry	f’	_m = 0.317 f_b ^0.531 f_m ^0.208	Dharek et al. ^[18]	2021	HCB	Conv. Concrete.	2600 × 845 × 152.	2	8.86	5.3	23.5	Axial load.
Costigan et al. ^[64]	Calibrated for fired clay brick wallette	f’_m = 0.56 f_b ^0.53 f_m ^0.5	Hasan et al. ^[19]	2021	HCB Brick	Conv. Concrete; Clay.	300 × 200 × 150–1200 × 750 × 150	24	7.5–19.2 5.8		7.5	Axial load.
Zhou et al. ^[68]	Calibrated for HCB wallette	f’_m = 0.886 f_b ^0.75 f_m	Gumaste et al. ^[15]	2007	Brick	Table moulded; Wire-cut	520 × 600 × 105; 520 × 665 × 230	9	5.7 23.0	0.8–6.6 0.6–12.2	–	Axial load, elastic modulus.
^0.18	Watstein and Allen ^[21]	1970	Brick	Extruded wire-cut	940 × 685 × 94–3716 × 3200 × 97.	36	54.2–174.3	10.0–48.6	–	Axial load; slenderness ratio and eccentricity.
Kirtschig and Anstotz ^[22]	1991	SCB	Calcium silicate; Lightweight aggregate.	635 × 1000 × 115–3120 × 1000 × 115	64	20.9 4.1	5	–	Axial load; slenderness ratio and eccentricity.
Hendry and Malek ^[58]	1987	Brick	Clay; Lightweight AAC	590 × 665 × 102 590 × 665 × 215	48	28.8–92.4 4.4	17.6; 27.4	–	Axial load; stress–strain
Fattal and Cattaneo ^[59]	1976	Brick HCB	Wire-cut Conv. Concrete	2438 × 812 × 90 2438 × 812 × 140	56	90.2 8.5	10.4	–	Axial load; stress–strain.
Khan et al. ^[57]	2023	Brick	Fired-clay	530 × 410 × 75; 445 × 445 × 75	18	16.1–20.2	5.0; 6.7	–	Axial load.
Milani et al. ^[60]	2021	Brick	Clay	965 × 580 × 140	8	14.6–19.6	5.8	–	Axial load; stress–strain.
Calderón et al. ^[61]	2023	Brick	Multi-perforated clay	745 × 745 × 140	9	19.5–22.3	7.6–28.0	–	Axial load; stress–strain.
Bergami and Nuti ^[62]	2015	Brick	Clay	1010 × 1010 × 260; 770 × 770 × 120	48	10.4–23.3	23.4; 11.7	–	Axial load.
Jafari et al. ^[63]	2022	Brick	Clay; CS	430 × 475 × 100; 880 × 300 × 100 210 × 180 × 100	54	13.1–36.4		–	Axial load; stress–strain; shear compression.
Costigan et al. ^[64]	2015	Brick	Fired-clay		5	12.7	1.4–22.2	–	Axial load; stress–strain.
Zhu et al. ^[65]	2017	HCB	Conv. concrete	990 × 590 × 190	6	25.75	15.55	-	Axial load.
Sandoval et al. ^[66]	2011	Brick	Clay	238 × 300 × 35; 896 × 300 × 35.	36	32.5	7.3	–	Axial load; slenderness ratio and eccentricity.
Mohammed et al. ^[67]	2009	Brick	Fired-clay	1700 × 1700 × 102	12	80	5.3–11.6		Axial load; stress–strain; opening.
Zhou et al. ^[68]	2017	HCB	Conv. concrete	990 × 590 × 190	24	14.1–31.1	6.3; 15.5	–	Axial load; stress–strain.
Thamboo and Dhanasekar ^[69],	2019	Brick	Clay; Compressed-earth	410 × 430 × 100; 590 × 570 × 140	40

References

Syiemiong, H.; Marthong, C. A review on improved construction methods for clay-brick and concrete-block ordinary masonry buildings. J. Struct. Integr. Maint. 2021, 6, 67–83.
Henrique Nalon, G.; Santos, C.F.R.; Pedroti, L.G.; Ribeiro, J.C.L.; de Souza Veríssimo, G.; Ferreira, F.A. Strength and failure mechanisms of masonry prisms under compression, flexure and shear: Components’ mechanical properties as design constraints. J. Build. Eng. 2020, 28, 101038.
Doran, B.; Karslioglu, M.; Unsal Aslan, Z.; Vatansever, C. Experimental and Numerical Investigation of Unreinforced Masonry Walls with and without Opening. Int. J. Archit. Herit. 2023, 17, 1833–1854.
Huang, D.; Albareda, A.; Pons, O. Experimental and Numerical Study on Unreinforced Brick Masonry Walls Retrofitted with Sprayed Mortar under Uniaxial Compression. Buildings 2023, 13, 122.
Zahra, T.; Dhanasekar, M. A generalised damage model for masonry under compression. Int. J. Damage Mech. 2016, 25, 629–660.
Zahra, T.; Thamboo, J.; Asad, M. Compressive strength and deformation characteristics of concrete block masonry made with different mortars, blocks and mortar beddings types. J. Build. Eng. 2021, 38, 102213.
Fortes, E.S.; Parsekian, G.A.; Fonseca, F.S. Relationship between the Compressive Strength of Concrete Masonry and the Compressive Strength of Concrete Masonry Units. J. Mater. Civ. Eng. 2015, 27, 04014238.
Nalon, G.H.; Ribeiro, J.C.L.; Pedroti, L.G.; da Silva, R.M.; de Araújo, E.N.D.; Santos, R.F.; de Lima, G.E.S. Review of Recent Progress on the Effects of High Temperatures on the Mechanical Behavior of Masonry Prisms. Infrastructures 2023, 8, 112.
Mohamad, G.; Lourenço, P.B.; Roman, H.R. Mechanics of hollow concrete block masonry prisms under compression: Review and prospects. Cem. Concr. Compos. 2007, 29, 181–192.
Ramamurthy, K.; Sathish, V.; Ambalavanan, R. Compressive strength prediction of hollow concrete block masonry prisms. ACI Struct. J. 2000, 97, 61–67.
Sarhat, S.R.; Sherwood, E.G. The prediction of compressive strength of ungrouted hollow concrete block masonry. Constr. Build. Mater. 2014, 58, 111–121.
Zahra, T.; Thamboo, J.; Asad, M.; Song, M. Analytical stress–strain model of reinforced concrete masonry wallettes under axial compression. Structures 2021, 34, 2922–2935.
Camacho, J.S.; Logullo, B.G.; Parsekian, G.A.; Soudais, P.R.N. The influence of grouting and reinforcement ratio in the concrete block masonry compressive behavior. Rev. IBRACON Estrut. Mater. 2015, 8, 341–364.
Fortes, E.S.; Parsekian, G.A.; Camacho, J.S.; Fonseca, F.S. Compressive strength of masonry constructed with high strength concrete blocks. Rev. IBRACON Estrut. Mater. 2017, 10, 1273–1319.
Gumaste, K.S.; Rao, K.S.N.; Reddy, B.V.V.; Jagadish, K.S. Strength and elasticity of brick masonry prisms and wallettes under compression. Mater. Struct. Constr. 2007, 40, 241–253.
Keshava, M.; Raghunath, S.R. Experimental Investigations on Axially and Eccentrically Loaded Masonry Walls. J. Inst. Eng. Ser. A 2017, 98, 449–459.
Amalkar, M.S.; Renukadevi, M.V.; Jagadish, K.S.; Basutkar, S.M. Effect of slenderness and eccentricity on the strength of concrete block masonry: An experimental investigation. SN Appl. Sci. 2020, 2, 1046.
Dharek, M.S.; Raghunath, S.; Ashwin, C.P. Experimental behaviour of unreinforced and reinforced concrete block masonry walls under uniaxial compression. Mater. Today Proc. 2021, 46, 2462–2467.
Hasan, M.; Saidi, T.; Sarana, D. Bunyamin The strength of hollow concrete block walls, reinforced hollow concrete block beams, and columns. J. King Saud Univ.—Eng. Sci. 2021, 34, 523–535.
Hasan, S.S.; Hendry, A. Effect of Slenderness and Eccentricity on the Compressive Strength of Walls. In Proceedings of the Fourth International Brick Masonry Conference, Brugge, Belgium, 26–28 April 1976.
Watstein, D.; Allen, M.H. Structural performance of clay masonry assemblages built with high-bond organic-modified mortars. In Proceedings of the Second International Brick Masonry Conference, Stoke-on-Trent, UK, 12–15 April 1970; pp. 99–112.
Kirtschig, K.; Anstötz, W. Kinckuntersuchungen an mauerwerksproben. In Proceedings of the Nineth International Brick/Block Masonry Conference, Berlin, Germany, 13–16 October 1991; pp. 202–209.
Turnšek, V.; Čačovič, F. Some experimental results on the strength of brick masonrywalls. In Proceedings of the 2nd International Brick Masonry Conference, Stoke-on-Trent, UK, 12–15 April 1971; pp. 149–156.
BS EN 1996-1-1:2005; Eurocode 6: Design of Masonry Structures—Part 3: General Rules for Reinforced and Unreinforced Masonry Structures. British Standards Institution: London, UK, 2005.
CSA S304; Design of Masonry Structures. Canadian Standards Association (CSA): Mississauga, ON, Canada, 2014.
AS 3700; Design of Masonry Structures. Australian Standards: Sydney, Australia, 2018.
Syiemiong, H.; Marthong, C. Effect of moisture on the compressive strength of low-strength hollow concrete blocks. Comput. Concr. 2019, 23, 267–272.
Mohamad, G.; Fonseca, F.S.; Vermeltfoort, A.T.; Martens, D.R.W.; Lourenço, P.B. Strength, behavior, and failure mode of hollow concrete masonry constructed with mortars of different strengths. Constr. Build. Mater. 2017, 134, 489–496.
Han, L.C.; Bin Mirasa, A.K.; Saad, I.; Bolong, N.B.; Asman, N.S.A.B.; Asrah, H.B.; Bin Abdullah, E.S.R. Use of compressed earth Bricks/Blocks in load-bearing masonry structural systems: A review. Mater. Sci. Forum 2020, 997, 9–19.
Nalon, G.H.; Ribeiro, J.C.L.; Pedroti, L.G.; da Silva, R.M.; de Araújo, E.N.D.; Santos, R.F.; de Lima, G.E.S. Review of recent progress on the compressive behavior of masonry prisms. Constr. Build. Mater. 2022, 320, 126181.
Hendry, E.A.W. Masonry walls: Materials and construction. Constr. Build. Mater. 2001, 15, 323–330.
Soleymani, A.; Najafgholipour, M.A.; Johari, A. An experimental study on the mechanical properties of solid clay brick masonry with traditional mortars. J. Build. Eng. 2022, 58, 105057.
Chaipanich, A.; Chindaprasirt, P. The properties and durability of autoclaved aerated concrete masonry blocks. In Eco-Efficient Masonry Bricks and Blocks: Design, Properties and Durability; Woodhead Publishing: Sawston, UK, 2015; pp. 215–230.
Arif Kamal, M. Analysis of autoclaved aerated concrete (AAC) blocks with reference to its potential and sustainability. J. Build. Mater. Struct. 2020, 7, 76–86.
Ma, G.; Huang, L.; Yan, L.; Kasal, B.; Chen, L.; Tao, C. Experimental performance of reinforced double H-block masonry shear walls under cyclic loading. Mater. Struct. Constr. 2017, 50, 70.
Al-Fakih, A.; Mohammed, B.S.; Liew, M.S.; Alaloul, W.S. Physical properties of the rubberized interlocking masonry brick. Int. J. Civ. Eng. Technol. 2018, 9, 656–664.
Al-Fakih, A.; Mohammed, B.S.; Nuruddin, F.; Nikbakht, E. Development of Interlocking Masonry Bricks and its’ Structural Behaviour: A Review Paper. IOP Conf. Ser. Earth Environ. Sci. 2018, 140, 12127.
Al-Fakih, A.; Mohammed, B.S.; Al-Shugaa, M.A.; Al-Osta, M.A. Experimental investigation of dry-bed joints in rubberized concrete interlocking masonry. J. Build. Eng. 2022, 58, 105048.
Al-Fakih, A.; Wahab, M.M.A.; Mohammed, B.S.; Liew, M.S.; Wan Abdullah Zawawi, N.A.; As’ad, S. Experimental study on axial compressive behavior of rubberized interlocking masonry walls. J. Build. Eng. 2020, 29, 101107.
Saari, S.; Bakar, B.H.A.; Surip, N.A. Factors of non-uniform properties of interlocking compressed earth brick units. Dev. Built Environ. 2021, 5, 100042.
Jos, R.; Lukito, M.M. Influence of Water Absorption on Properties of AAC and CLC Lightweight Concrete Brick. In Proceedings of the 4th ASEAN Civil Engineering Conference, Yogyakarta, Indonesia, 22–23 November 2011.
Bhosale, A.; Zade, N.P.; Sarkar, P.; Davis, R. Mechanical and physical properties of cellular lightweight concrete block masonry. Constr. Build. Mater. 2020, 248, 118621.
Chica, L.; Alzate, A. Cellular concrete review: New trends for application in construction. Constr. Build. Mater. 2019, 200, 637–647.
Lourenço, P.B.; Avila, L.; Vasconcelos, G.; Alves, J.P.P.; Mendes, N.; Costa, A.C. Experimental investigation on the seismic performance of masonry buildings using shaking table testing. Bull. Earthq. Eng. 2013, 11, 1157–1190.
Al-Fakih, A. Experimental and analytical assessment on rubberized concrete interlocking grouted masonry walls under eccentric loading. Structures 2022, 44, 893–903.
Zhai, X.; Stewart, M.G. Structural reliability analysis of reinforced grouted concrete block masonry walls in compression. Eng. Struct. 2010, 32, 106–114.
Bean Popehn, J.R.; Schultz, A.E.; Lu, M.; Stolarski, H.K.; Ojard, N.J. Influence of transverse loading on the stability of slender unreinforced masonry walls. Eng. Struct. 2008, 30, 2830–2839.
Parisi, F.; Augenti, N. Assessment of unreinforced masonry cross sections under eccentric compression accounting for strain softening. Constr. Build. Mater. 2013, 41, 654–664.
Adam, J.M.; Brencich, A.; Hughes, T.G.; Jefferson, T. Micromodelling of eccentrically loaded brickwork: Study of masonry wallettes. Eng. Struct. 2010, 32, 1244–1251.
Yokel, F.Y.; Dikkers, R.D. Strength of Load Bearing Masonry Walls. J. Struct. Div. 1971, 97, 1593–1609.
Sandoval, C.; Roca, P. Empirical equations for the assessment of the load-bearing capacity of brick masonry walls. Constr. Build. Mater. 2013, 44, 427–439.
Sandoval, C.; Roca, P. Study of the influence of different parameters on the buckling behaviour of masonry walls. Constr. Build. Mater. 2012, 35, 888–899.
TMS 402/ASCE 5/ACI 530; Building Code Requirements and Specification for Masonry Structures. Masonry Standards Joint Committee (MSJC): New York, NY, USA, 2011.
ENV: 1996-1-1-1995; Eurocode 6-Design of Masonry Structures—Part 3: Simplified Calculation Methods for Unreinforced Masonry Structures. British Standards Institution: London, UK, 1996.
Garzón-Roca, J.; Marco, C.O.; Adam, J.M. Compressive strength of masonry made of clay bricks and cement mortar: Estimation based on Neural Networks and Fuzzy Logic. Eng. Struct. 2013, 48, 21–27.
Bennett, R.M.; Boyd, K.A.; Flanagan, R.D. Compressive Properties of Structural Clay Tile Prisms. J. Struct. Eng. 1997, 123, 920–926.
Khan, N.A.; Aloisio, A.; Monti, G.; Nuti, C.; Briseghella, B. Experimental characterization and empirical strength prediction of Pakistani brick masonry walls. J. Build. Eng. 2023, 71, 106451.
Hendry, A.W.; Malek, M.H. Characteristic compressive strength of brickwork walls from collected test results. Mason. Int. 1986, 7, 15–24.
Fattal, S.G.; Cattaneo, L.E. Structural Performance of Masonry Walls Under Compression and Flexure; US Department of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1976.
Milani, A.S.; Lübeck, A.; Mohamad, G.; da Silva Santos Neto, A.B.; Budny, J.; Kosteski, L.E. Case study of prototype and small-scale model behavior of clay blocks masonry under compression. Case Stud. Constr. Mater. 2021, 15, e00684.
Calderón, S.; Sandoval, C.; Araya-Letelier, G.; Aguilar, V. A detailed experimental mechanical characterization of multi-perforated clay brick masonry. J. Build. Eng. 2023, 63, 105505.
Bergami, A.V.; Nuti, C. Compression tests on masonry walls realized with a single or double masonry panel. J. Civ. Eng. Archit. Res. 2015, 2, 802–809.
Jafari, S.; Rots, J.G.; Esposito, R. A correlation study to support material characterisation of typical Dutch masonry structures. J. Build. Eng. 2022, 45, 103450.
Costigan, A.; Pavía, S.; Kinnane, O. An experimental evaluation of prediction models for the mechanical behavior of unreinforced, lime-mortar masonry under compression. J. Build. Eng. 2015, 4, 283–294.
Zhu, F.; Zhou, Q.; Wang, F.; Yang, X. Spatial variability and sensitivity analysis on the compressive strength of hollow concrete block masonry wallettes. Constr. Build. Mater. 2017, 140, 129–138.
Sandoval, C.; Roca, P.; Bernat, E.; Gil, L. Testing and numerical modelling of buckling failure of masonry walls. Constr. Build. Mater. 2011, 25, 4394–4402.
Mohammed, B.S.; Abu Bakar, B.H.; Choong, K.K. The Effects of Opening on the Structural Behavior of Masonry Wall Subjected to Compressive Loading—Strain Variation. Open Civ. Eng. J. 2009, 3, 62–73.
Zhou, Q.; Wang, F.; Zhu, F.; Yang, X. Stress–strain model for hollow concrete block masonry under uniaxial compression. Mater. Struct. Constr. 2017, 50, 106.
Thamboo, J.A.; Dhanasekar, M. Correlation between the performance of solid masonry prisms and wallettes under compression. J. Build. Eng. 2019, 22, 429–438.