RMn2Hx Hydrides: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Camila Xu and Version 1 by Andrzej Budziak.

Laves phases crystallize in simple structures and are very common intermetallic phases that can form from combinations of elements throughout the periodic table, giving a huge number of known examples. A special feature of AB2 or AB5 phases is the ability to absorb hydrogen.

  • metal hydrides
  • Laves phases
  • hydrogen storage
  • X-ray diffraction

1. Introduction

1.1. Laves Phases

One of the most widespread and most studied groups of solids is the metallic phases. These phases are divided into simple phases (metallic elements), solid solutions and intermetallic phases. Solid solutions include substitution and interstitial solutions. Interstitial solutions are formed when relatively small atoms of a solute element do not occupy atomic positions, but positions in the interstitial voids of the solvent. A characteristic feature of solid solutions is that they retain the crystallographic structure of the solvent. Intermetallic phases assume crystal structures different from those of the individual components of the phase. In general, intermetallic phases are described by the formula AnBm and are divided into the following types according to the adopted classification [1,2,3][1][2][3]:
  • Phases with a dense filling of space (Laves phases), which are classified according to the size of atoms/ions;
  • Electronic phases, which are classified according to the electron concentration, i.e., the ratio of the number of valence electrons to the number of atoms in the unit cell;
  • Phases with mixed, metallic-ionic and metallic-covalent bonds.
The most important properties of the Laves phases include the following:
  • They are metal alloys with the general stoichiometric formula AB2;
  • The main factor influencing their formation is the ratio of the radii of the component atoms, and rA/rB is equal, theoretically, to 1.225. In fact, this ratio for the Laves phases is within the range of 1.05–1.68 Å. Here, A refers to larger atoms (e.g., rare earths), and B refers to smaller atoms (e.g., Cu, Zn, Fe, Mn, Cr, etc.);
  • They do not create secondary solutions;
  • They exhibit an almost purely metallic type of bonding;
  • They are phases with the densest space filling;
  • They crystallize in one of three homothetic types, C14, C15 and C36, as determined by the value of the electron concentration [4].
The RMn2 intermetallic compounds crystallize either in the hexagonal C14 type for R = Pr, Nd, Sm, Ho, Er, Tm and Lu or in the cubic C15 type for R = Y, Sm, Gd, Tb, Dy and Ho [5,6,7,8,9,10,11,12,13,14][5][6][7][8][9][10][11][12][13][14]. Other elements (A: La, Ce, Eu and Yb) do not form stable intermetallic compounds with Mn [15].

1.2. Structural and Magnetic Properties of RMn

2

Compounds

The RMn2 compounds have been widely studied because of their very interesting structural and magnetic properties. Changes of the unit cells for RMn2 as a function of the temperature are presented in Figure 1a [16]. For the (Tb, Gd, Sm, Nd, Pr, Y)Mn2 compounds, the first-order phase transition is observed, and temperature dilatometer and X-ray diffraction measurements revealed significant increases in the volume of unit cells of these alloys at temperatures below 105 K. The magnetic ordering was also observed below the temperatures of the structural changes [17,18,19][17][18][19]. The largest, an almost 5% change in volume, was recorded for YMn2. This significant magneto-volume effect is related to the appearance of a well-localized magnetic moment in the Mn sublattice (~2.7μB) below the magnetic ordering temperature [20]. The (Er, Ho, Dy)Mn2 compounds do not show changes in the volume cell; they undergo a second-order phase transition in the temperature range of 15–35 K [14,21][14][21].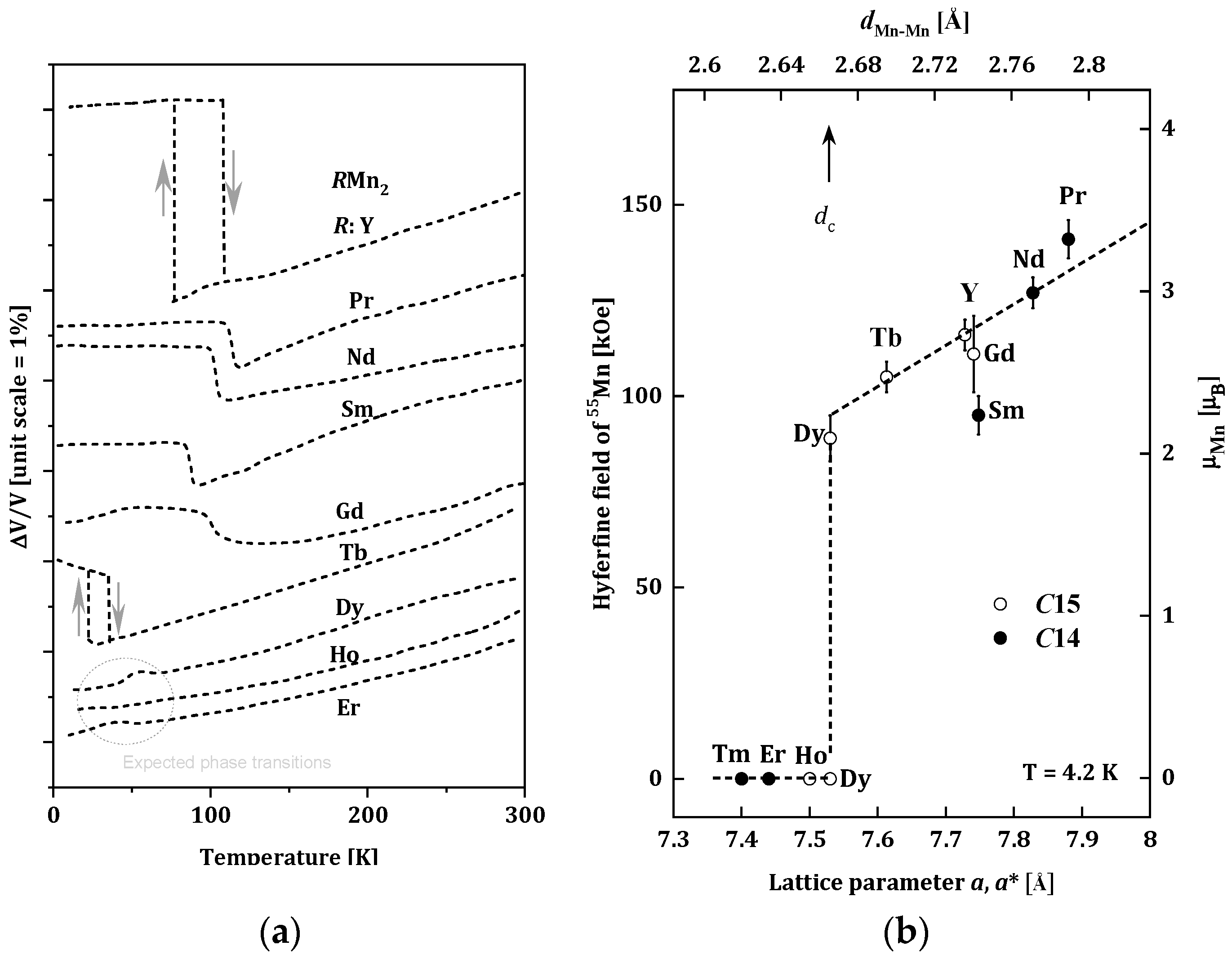
Energies 16 07383 g001
Figure 1. (a) Changes of the unit cells for RMn2 as a function of the temperature for RMn2 [16]; (b) Relation between the 55Mn hyperfine field Hself and the lattice parameter of RMn2 at 4.2 K. The transferred hyperfine fields from rare-earth moments are subtracted from the observed ones. The effective lattice parameter of C14 compounds (closed circles) is given by aeff = (3a2c)1/3. The scale for the estimated Mn moment from Hself is given on the right-hand side [22].
The type of the phase transition can be related to the occurrence of a magnetic moment of Mn atoms or its absence. The measurements of the hyperfine field on the 55Mn nuclei in RMn2 compounds carried out by Yoshimura (Figure 1b) indicate that below a certain distance of ~2.66 Å between the nearest Mn atoms (dMn-Mn), the localized magnetic moment of the Mn atoms is not observed. This distance is called the critical distance and denoted as dc [22]. Based on the dMn-Mn distance, RMn2 compounds can be divided into three groups [23]:
  • dMn-Mn < dc, (LuMn2, ErMn2, TmMn2), where the Mn subnet is non-magnetic, and the Er and Tm sublattices are ferromagnetic [24];
  • dMn-Mn > dc, (NdMn2, PrMn2), where the dominant Mn magnetic sublattice is stable and enforces antiferromagnetic ordering in the sublattice of R-atoms with the R-Mn type interaction [25];
  • dMn-Mn ~ dc, (GdMn2, TbMn2[32][33][34].
The magnetism of the RMn2 compounds is related to the electronic structure of Mn and R atoms. Mn has an unfilled outer 3d electron shell affecting the crystalline field from other ions. However, in the R atoms, the unfilled inner 4f electron shell is shielded by the 5p outer shell, which facilitates the behavior similar to that noted for the free ion. In the RMn2 compounds, three types of exchange interactions can be distinguished as follows:
  • Between 3d–3d magnetic moments (Mn–Mn),
  • Between 3d–4f moments (Mn–R),
  • , DyMn2, HoMn2, YMn2), where the Mn sublattice is on the verge of stability. Generally, non-collinear magnetic structures are observed in this group of compounds. In some cases (TbMn2, DyMn2, HoMn2), only a part of the Mn atoms carries a magnetic moment [20,26,27,28,2029,30,][2631,][
  • Between localized 4f–4f2732,]33,34][[28][29][30 moments (R][31–R]).
The strongest among the above is the 3d–3d exchange interaction, as evidenced by the high temperature of ordering of the magnetic relationship with non-magnetic rare earths (YMn2, TN ≈ 105 K). The band model, which is applicable here, assumes that the difference in concentration between electrons with spins ↓ and ↑ is responsible for the formation of the magnetic moment. The weakest is the 4f–4f interaction, as indicated by low temperatures of magnetic ordering of the ErMn2 and TmMn2 compounds with the non-magnetic Mn sublattice (Figure 1a,b). The R atoms having an unfilled 4f electron shell are characterized by well-localized magnetic moments; the wave functions that describe them have a short range in comparison to the distance between atoms (magnetic moments). The magnitude of the interaction of 4f–4f depends on the density of the polarized conduction electrons; their oscillating nature as a function of distance is described by the RKKY theory. The magnetic interaction 3d–4f has an intermediate value between 3d–3d and 4f–4f. It occurs mainly through the polarization of electrons of 5d rare earth atoms [35].

1.3. Hydrogen in Metals

Rare earth (R) metals react with hydrogen forming stable di- and trihydrides. The RH2 dihydrides are very stable, with reported formation enthalpies of about −200 kJ/molH2; thus, they decompose in a vacuum, releasing hydrogen and forming individual RE metals at very high temperatures only [36]. On the other hand, manganese, which is also the main building block of the discussed RMn2Hx structures, behaves differently under the influence of hydrogen in comparison to RHx. At ambient pressure conditions and room temperature, the subhydride Mn2H is the only stable compound. With increasing pressure, MnH is stabilized, and then hydrogen-rich hydrides appear at higher pressure [37]. A simplified scheme of hydrogen penetration into the crystal structure of the metal (intermetallic compound) can be divided into three stages (Figure 2): (a) Physisorption: gaseous hydrogen molecules interact with electrons on the metal surface using weak attractive van der Waals forces; (b) Chemical adsorption: hydrogen molecules dissociate, overcoming the surface energy barrier, and form a metallic hydrogen bond; (c) Absorption: in this step, the chemisorbed hydrogen atom can jump to the subsurface layer to finally diffuse through the crystalline structure of the metallic host [38].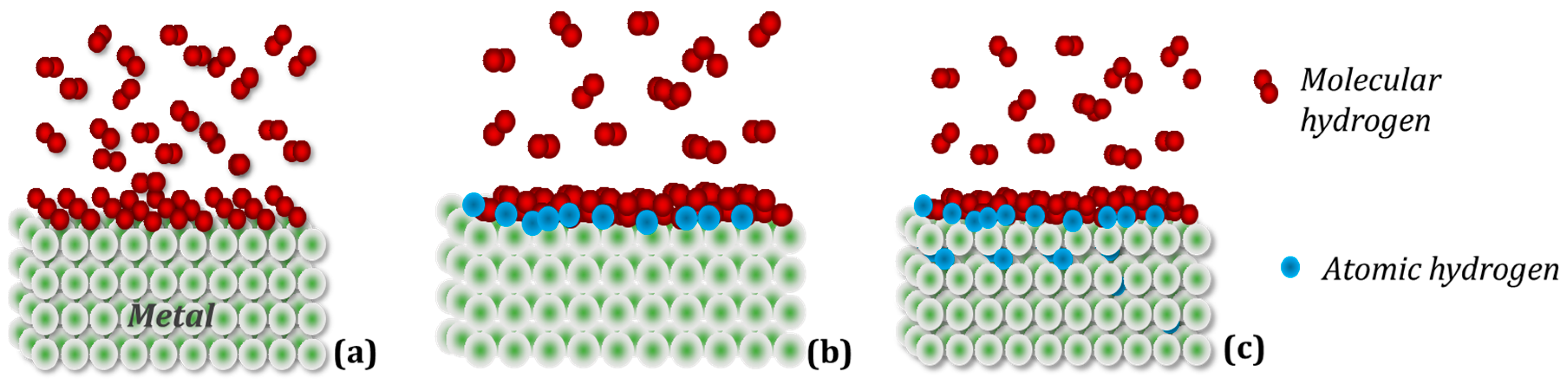
Energies 16 07383 g002
Figure 2. Simplified mechanism of hydrogen absorption in metal. (a) Physical adsorption: hydrogen molecules adhere to the metal surface, forming several layers; (b) Chemical adsorption: dissociated hydrogen molecules of the layer in direct contact with the metal form chemical bonds with it; (c) Absorption: hydrogen atoms diffuse into the parent metal lattice.
After absorption, the hydrogen atoms/ions remain in the sites of the crystal structure until they are given a surplus of energy necessary to overcome the diffusion barrier as a result of thermal activation. Under these conditions, the diffusion coefficient satisfies the classical Arrhenius relationship: D = D0 exp (−Ea/kT), where D0 is the diffusion constant. Assuming the simple activated diffusion, the typical diffusion constant for H in intermetallic compounds equals 1–103 mm2/s and Ea = 45 kJ/mol at room temperature [39,40][39][40]. Researchers also point to the dependence of the D0 and the T on the structure on the structure of the metal. For example, for Pd (fcc structure), D0 = 2.9 × 10−3 cm2/s and Ea = 0.230 eV, while Do = 4.2 × 10−4 cm2/s and Ea = 0.40 eV for Fe (bcc structure) [41]. One of the first experiments indicating the dissociation of H2 molecules in the process of its absorption by metals was the study of the p-c-T relationship (hydrogen pressure-concentration-temperature) [39]. In numerous metal hydrides, hydrogen atoms are characterized by high mobility already at room temperature, especially when the number of available positions is greater than the number of hydrogen atoms. Hydrogen atoms can jump from one position to another without creating a crystallographic ordered structure—the positioning is accidental. The frequency of hydrogen jumps is huge (e.g., in vanadium hydrides at room temperature, it is ~1010–1012 Hz) [39]. With the lowering of the hydride temperature, the frequency decreases. Therefore, it may also happen that hydrogen atoms occupy selected positions in an orderly manner, and they create a superstructure. Skripov states that in many hydrides of the Laves phase, even two types of hydrogen jumping motions with different characteristic jump rates coexist. While the slower jump process is responsible for long-distance diffusion, the faster process corresponds to the localized movement of hydrogen over small groups of interstitial sites. In some of the Laves-phase compounds, the localized hydrogen motion is not ‘frozen out’ on the frequency scale of 107 to 108 Hz down to 20 K [42]. At low temperatures, there is also the possibility of non-activation, tunnel transitions of the hydrogen atom from one position to another [38,43,44][38][43][44]. Figure 3a shows the typical hydrogen absorption isotherms in metal. The isotherms form a phase diagram of the equilibrium pressure as a function of the hydrogen concentration Peq (x), in which three essential areas can be distinguished: (i) the α region is the “solid” solution of hydrogen in the parent metal, where the hydrogen pressure p increases with the hydrogen content x according to Sievert’s law p = (Ks c)2 (K—Sievert’s constant, c—hydrogen concentration), (ii) the two-phase region (α + β) and (iii) the β region—metal hydride. As the temperature increases, the latter narrows and disappears at the critical temperature Tcrit, which is characteristic for a given element. The isotherms in the middle region show a hydride characteristic plateau, corresponding to the equilibrium pressure as a function of the hydrogen concentration.
Energies 16 07383 g003
Figure 3. (a) Schematic plot of hydrogen absorption in metal (p-c-T isotherms). Peq—gas pressure, c—hydrogen concentration in the metal; (b) Construction of the Van’t Hoff relation. Based on [45,46][45][46].
The equilibrium pressure zone is ideally suited for the isothermal absorption and desorption of hydrogen from metal. The state of equilibrium can be described by a phase diagram analogous to the Van der Waals diagram of the non-ideal gas. Peq equilibrium pressure is associated with changes in enthalpy (ΔH) and entropy (ΔS) in the two-phase region via the empirical temperature of the Van’t Hoff relationship (Figure 3b) [45,46][45][46]. For a typical equilibrium pressure, e.g., for PdHx—hydride at 423 K, it is 0.1 MPa, and it is 1.0 MPa at 518 K. The critical point of this hydride is Tcrit = 565 K at x ≈ 0.25 H/f.u. [39].

2. RMn2Hx Hydrides

2.1. Localization of Hydrogen

The physical properties of rare earth hydrides with manganese RMn2Hx largely coincide with the properties of metal hydrides (MHx). Also, alloys of RMn2 compounds absorb hydrogen very easily. At close to atmospheric hydrogen pressure and temperatures above 100 °C, it is possible to achieve a hydrogen concentration of ~4.5 H/f.u. [48][47]. As noted in metal hydrides, hydrogen occupies the interatomic sites of the elements that comprise the RMn2 unit cell. There are three types of tetrahedral sites in RMn2 compounds: A2B2, AB3 and B4, where A and B represent atoms of R and Mn, respectively, surrounding the site (Figure 4). The largest and at the same time most willingly filled by hydrogen site (below x ≈ 3.5 H/f.u.) is the A2B2 type. For x ≳ 3.5 H/f.u., there is also a tendency to fill smaller sites, such as AB3 sites [49,50,51,52][48][49][50][51]. However, no B4 site filling was observed. The same types of sites occur in both C14 and C15 types of Laves phases. When filling the sites, hydrogen occupies crystallographic positions (Table 1).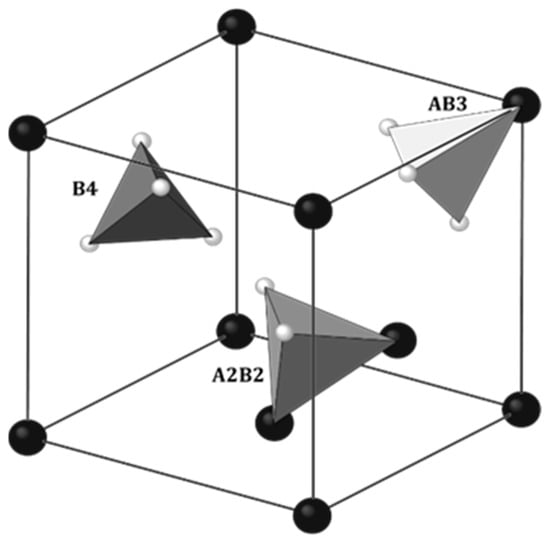
Energies 16 07383 g004
Figure 4. Three crystallographic positions accessible for hydrogen in C15 Laves phase: 96g (inside of A2B2 tetrahedra), 32e (inside of AB3 tetrahedra) and 8b (inside of B4 tetrahedra). The Fd3𝑚3¯� space group. Some atoms were removed for clarity. Big, dark balls: R; small, bright balls: Mn. Based on [51][50].
Table 1.
Hydrogen positions in C14 and C15 phases.
Laves Phase Positions of Hydrogen Number of Sites/f.u.
A2B2 AB3 A2B2 AB3
C14 24l, 12k, 6h1, 6h2 12k, 4f 12 4
C15 96g 32e
Although the number of sites is significant, every site cannot be occupied by hydrogen. Two criteria are useful: (i) the Switendick criterion [53][52] states that the distance dH-H must be larger than ~2.1 Å and (ii) the Westlake criterion indicates that the radius of the sphere available for hydrogen cannot be less than ~0.37 Å. [54][53]. As an effect, criteria preclude occupancy of A2B2 tetrahedrons that have a common wall, and the B4 site is not available for hydrogen due to size restrictions. The Switendick criterion, confirmed in neutron measurements [55[54][55],56], largely determines the maximum content of absorbed hydrogen. The theoretically determined maximum hydrogen concentration in RT2Hx (R: rare earth, T: transition metal = Y, Mn) compounds is therefore 6.0 H/f.u. [57][56]. Only the use of ultra-high hydrogen pressures of the order of 103 MPa led to the formation of RMn2H6 hydrides; the first being YMn2H6 [58,59][57][58]. Highly hydrogenated (x ≳ 4.5 H/f.u.) compounds show different physical properties compared to low-hydrogen compounds (x ≲ 4.5 H/f.u.) [60,61][59][60] and will not be discussed in this study.

2.2. Sample Preparation and Dependence of ΔV/V versus Hydrogen Content

In the discussed hydrides, the sample preparation was similar and usually involved the following scenario. The host materials (RMn2) were prepared from high purity elements using the standard induction melting technique under argon atmosphere. Next, materials were usually annealed to obtain a single-phase compound. The RMn2 samples were saturated with hydrogen using a standard volumetric method (Sievert) to obtain RMn2Hx hydrides in the typical range of x: 0 < x < 4.3–4.5 [7,8,9,55,62,63,64,65,66,67][7][8][9][54][61][62][63][64][65][66]. The first test after hydrogen saturation was XRD measurements at 300 K. As a representative example, the HoMn2Hx_C15 diffractogram is presented in Figure 5a. The most visible effect of hydrogen absorption by the sample is the shift of the diffraction lines towards smaller angles (in 2 theta), which means an increase in the distance between atoms in the cell, and consequently an increase in the unit volume of the cell with x.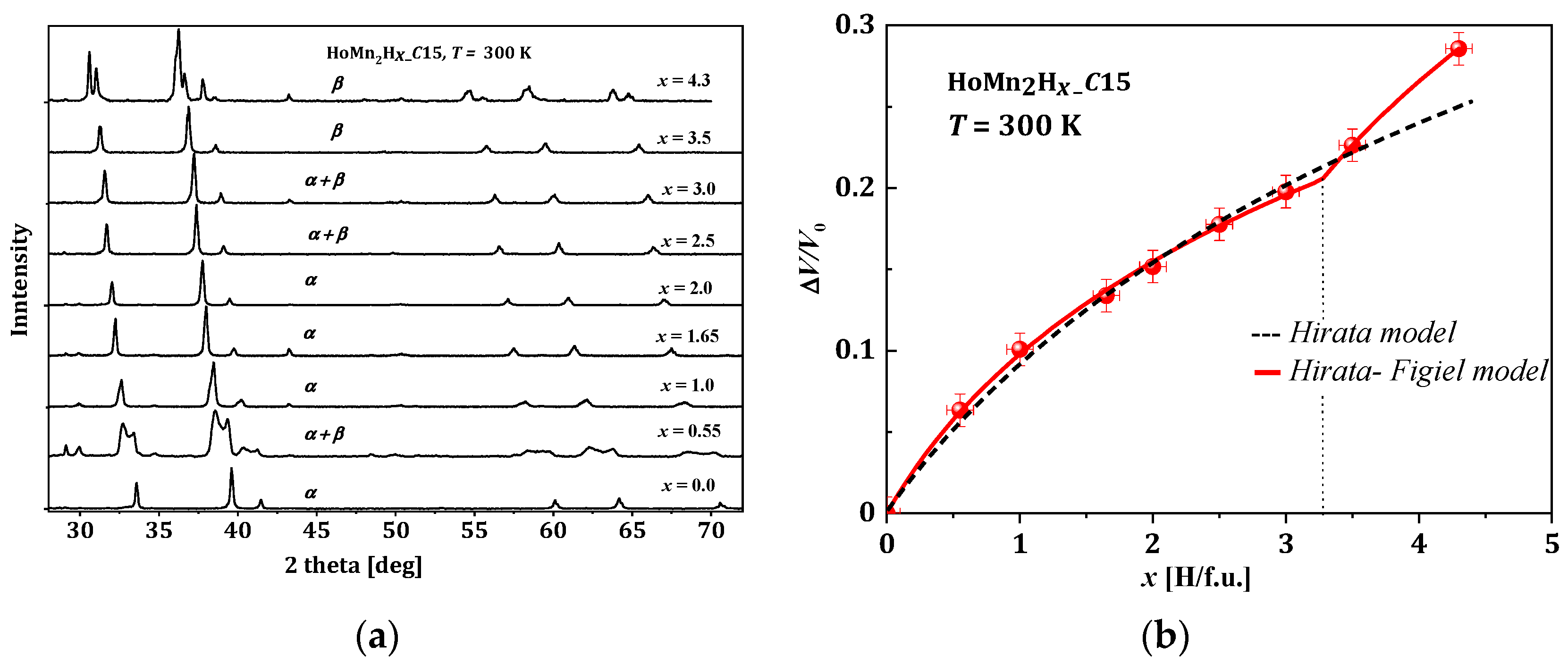
Energies 16 07383 g005
Figure 5. HoMn2Hx. (a) The XRD patterns for different x; here, α represents the cubic phase (𝐹𝑑3), and β represents the rhombohedral phase (𝑅3); (b) Relative change in the unit cell volume as a function of x [66][65].
Even at room temperature, the RMn2Hx hydrides do not persist in the crystallographic structure of the host compound. For the HoMn2Hx_C15 hydride, a combination of the cubic (α) and rhombohedral distortion (β) is observed (Figure 5a). The obtained results are in agreement with [68][67]. To compare lattice parameters of hydrides with different crystallographic structures, their parameters were converted into parameters of the pseudo-cubic cell considering abundance phases, if the system is not a single-phase system. For example, the lattice parameters of the rhombohedral phase were converted into lattice parameters 𝑎*𝛿  of the pseudo-cubic phase according to the relationship reported below:
 
where aδ and cδ are lattice parameters of the rhombohedral phase (space group: 𝑅3, nr166, setting: 1) [66][65]. The relative volume change in unit cell versus hydrogen content in HoMn2Hx_C15 is depicted in Figure 5b. The first ‘model’ that attempted to describe the relation between ΔV/V0 and x was just a linear relationship. The next one, the Hirata model, only correctly reproduces the lowest range of x (0 < x < 3.0) (Figure 5b, dashed line) [69][68], and its development was proposed by Figiel et al. [51][50]. In the last one (farther: Hirata–Figiel model), the authors assume a two-stage approach to occupying interstitial sites (Figure 5b red line). Initially, with a characteristic parameter Xc < 3.0–3.5 H/f.u. (see below), the A2B2 type sites are filled (this part is identical with Hirata model). Next, above Xc > 3.0–3.5 H/f.u., the AB3 type sites are also occupied. It is represented by a characteristic break in the red curve (x~3.2 H/f.u., Figure 5). The Hirata-Figiel model is described according to the relationship described below [51][50].
 
where ΔV/V0 is the relative increase in unit cell volume; B0 is a parameter of the lattice contraction, a quantity analogous to the bulk modulus at starting concentration related to the intrinsic pressure; b is the first derivative with respect to concentration x: (Bx = B0 + bx); and P is the probability of filling the AB3 sites by hydrogen atoms for concentrations greater than Xc (P = 0 for x ≤ Xc) [34,51][34][50]. Fitted parameters for the RMn2Hx (R: Y, Dy, Gd, Tb, Ho) hydrides are presented in Table 2. For all compounds, the characteristic Xc belongs to the region of ~3.0–3.5 and probabilities of entering the AB3 interstitial sites P~0.6–0.9. This type of filling sites was also postulated in [50,51][49][50].
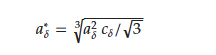
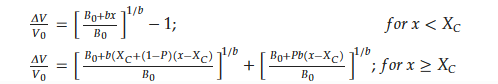
Table 2.
Fitted parameters for the Hirata-Figiel model.
Sample B0 b Xc P
YMn2Hx (300 K) * 9.24 9.63 3.25 0.77
DyMn2Hx (300 K) * 7.03 9.08 3.20 0.61
GdMn2Hx (300 K) * 9.43 10.01 3.06 0.52
TbMn2Hx (300 K) * 7.78 9.36 3.15 0.56
HoMn2Hx (300 K) * 6.93 8.90 3.33 0.88
HoMn2Hx_C14, (300 K) ** 4.7(6) 13(1) 3.48(3) 0.9(1)
HoMn2Hx_C14, (75 K) ** 6.1(2) 9 (1) 3.41(3) 0.8(1)
HoMn2Hx_C15, (300 K) *** 6.0(5) 10(1) 3.2(1) 0.6(1)
* [51][50] ** [7], *** [66][65].
The relative volume increase (ΔV/V0) of unit cells of hydrides determined at room temperature and depending on the hydrogen content in the sample is non-linear and can be described by the same function, indicating that this effect is determined only by the presence of hydrogen. The fits of the Hirata–Figiel model to the change in (ΔV/V0) depending on the hydrogen concentration for the various studied hydrides RMn2Hx are shown in Figure 6.
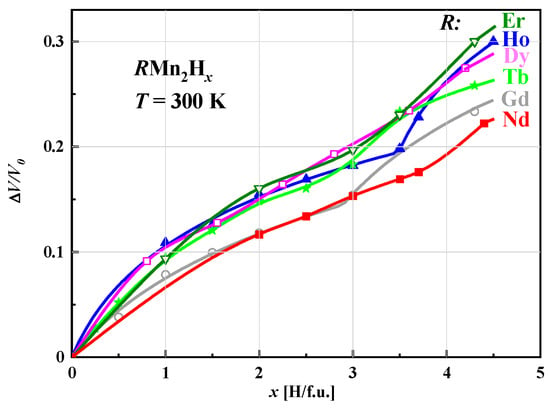Energies 16 07383 g006
Figure 6.
Comparison of relative volume change in unit cells for
R
Mn
2
H
x versus hydrogen content at RT = 300 K. Based on [7,51,65,66,67].
versus hydrogen content at RT = 300 K. Based on [7][50][64][65][66].
For x < 3.0 H/f.u., the curves, except for those corresponding to (Gd and Nd)Mn2Hx, are almost identical. At values greater than x ≈ 3.0 H/f.u., distinct behavior becomes visible with increasing x, especially for concentrations close to the maximum, where the relative increase in volume increases with the atomic number of the rare earth element.

2.3. Examples of Structural and Magnetic Transformations in RMn

2

H

x

With a temperature change, the RMn2Hx hydrides undergo complex phase transformations in many cases, which, combined with the often occurring multi-phase states, makes the interpretation of their X-ray diffraction magnetic transformation results extremely difficult. Some authors have even argued that it will never be possible [39]. One of the first hydride families to be studied over a wide range of x and temperature changes was YMn2Hx, showing a very wide range of structural transformations as a function of temperature. In contrast, TbMn2Hx hydride families show a very ‘modest’ spectrum of structural transformations. Very interesting are the structural and magnetic properties of HoMn2Hx hydrides, in which the base compound can crystallize in a C14 or C15 Laves phase structure, depending on the sample preparation [10].

References

  1. Laves, F. Theory of Alloy Phases; American Society for Metals: Metals Park, OH, USA, 1956; p. 12.
  2. Stein, F.; Palm, M.; Sauthoff, G. Structure and stability of Laves phases. Part I. Critical assessment of factors controlling Laves phase stability. Intermetallics 2004, 12, 713–720.
  3. Liu, C.T.; Zhu, J.H.; Brady, M.P.; McKamey, C.G.; Pike, L.M. Physical metallurgy and mechanical properties of transition-metal Laves phase alloys. Intermetallics 2000, 8, 1119–1129.
  4. Stein, F.; Leineweber, A. Laves phases: A review of their functional and structural applications and an improved fundamental understanding of stability and properties. J. Mater. Sci. 2021, 56, 5321–5427.
  5. YMn2 Crystal Structure, Springer Material. Available online: https://materials.springer.com/isp/crystallographic/docs/sd_0382661 (accessed on 8 October 2023).
  6. Talik, E.; Kulpa, M.; Winiarski, A.; Mydlarz, T.; Neumann, M. Electronic structure and magnetic properties of HoMn2 single crystals. J. Alloys Compd. 2001, 316, 51–57.
  7. Budziak, A.; Żurek, M.; Żukrowski, J.; Bałanda, M.; Pacyna, A.; Czapla, M. Influence of hydrogen on structural and magnetic properties of the hexagonal Laves phase HoMn2. J. Magn. Magn. Mater. 2012, 324, 735–741.
  8. Żukrowski, J.; Figiel, H.; Budziak, A.; Zachariasz, P.; Fisher, G.; Dormann, E. Structural and magnetic transformations in the GdMn2Hx hydrides. J. Magn. Magn. Mater. 2002, 238, 129–139.
  9. Figiel, H.; Budziak, A.; Żukrowski, J.; Fisher, G.; Kelemen, M.T.; Dormann, E. Structural and magnetic properties of TbMn2Hx hydrides. J. Alloys Compd. 2002, 335, 48–58.
  10. Nassau, K.; Cherry, L.V.; Wallace, W.E. Intermetallic compounds between lanthanons and transition metals of the first long period: I—Preparation, existence, and structural studies. J. Phys. Chem. Solid 1960, 16, 123–130.
  11. Wernick, J.H.; Geller, S. Rare-earth compounds with the MgCu2 structure. Trans. Met. Soc. AIME 1960, 218, 866.
  12. Wernick, J.H.; Haszko, S.E. Manganese rare earth compounds with the MgZn2 structure. J. Appl. Phys. 1961, 48, 207–209.
  13. Hardman, K.; Rhyne, J.J.; Malik, S.; Wallace, W.E. Site magnetization of cubic and hexagonal HoMn2. J. Appl. Phys. 1982, 53, 1944.
  14. Labroo, S.; Nausahad, A.; Robinson, P. Magnetic properties of RMn2 compounds (R=heavy rare earths). J. Appl. Phys. 1990, 67, 5292–5294.
  15. Malik, S.K.; Wallace, W.E. Magnetic behavior of cubic Laves phase RMn2 (R = Gd, Dy and Ho) compounds. J. Magn. Magn. Mater. 1981, 24, 23–28.
  16. Wada, H.; Nakamura, H.; Yoshimura, K.; Shiga, M.; Nakamura, Y. Stability of Mn moments and spin fluctuations in RMn2 (R: Rare earth). J. Magn. Magn. Mat. 1987, 70, 134.
  17. Shiga, M.; Wada, H.; Nakamura, Y. Magnetism and thermal expansion anomaly of RMn2 (R=Y, Gd, Tb, Ho and Er). J. Magn. Magn. Mat. 1983, 31–34, 119.
  18. Nakamura, J. Magnetovolume effects in Laves phase intermetallic compounds. J. Magn. Magn. Mat. 1983, 31–34, 829–834.
  19. Tagawa, Y.; Sakurai, J.; Komura, Y.; Wada, H.; Shiga, M.; Nakamura, Y. X-ray Study of Crystal Distortions in RMn2 Compounds (R: Y, Pr, Nd, Sm and Gd). J. Phys. Soc. Jpn. 1985, 54, 591.
  20. Shiga, M. Magnetism and spin fluctuations of Laves phase manganese compounds. Phys. B+C 1988, 149, 293–305.
  21. Gaidukova, I.Y.; Kruglyasher, S.B.; Markosyan, A.S.; Levitin, R.Z.; Pastuschenkov, Y.G.; Snegirev, V.V. Metamagnetism of the manganese subsystem in RMn2 intermetallic compounds. Sov. Phys. JEPT 1983, 57, 1083–1088.
  22. Yoshimura, K.; Shiga, M.; Nakamura, Y. NMR Study of Magnetic State of RMn2 Intermetallic Compounds. II. R=Heavy Rare-Earth. J. Phys. Soc. Jpn. 1986, 55, 3585–3595.
  23. Makarova, O.L.; Goncharenko, I.N.; Irodova, A.V.; Mirebeau, I.; Suard, E. Interplay of magnetic and hydrogen ordering in the hexagonal Laves hydrides. Phys. Rev B 2002, 66, 104423.
  24. Felcher, G.P.; Corliss, L.M.; Hastings, J.M. Investigation of the Magnetic Structure of ErMn2, TmMn2, TbNi2 by Neutron Diffraction. J. Appl. Phys. 1965, 36, 1001–1002.
  25. Ouladdiaf, B.; Ballou, R.; Deportes, J.; Lamaire, R.; Sayet, F. Effects of exchange frustrations in NdMn2. J. Phys. Cond. Matter 1992, 4, 4675–4686.
  26. Cywinski, R.; Kilcoyne, S.H.; Scott, C.A. Magnetic order and moment stability in YMn2. J. Phys. Cond. Matter 1991, 3, 6473–6488.
  27. Corliss, L.; Hastings, J. A Neutron Diffraction Investigation of the Magnetic Structure of TbMn2. J. App. Phys. 1964, 35, 1051–1053.
  28. Brown, P.J.; Ouladdiaf, B.; Ballou, R.; Deportes, J.; Markosyan, A.S. Mn moment instability in the TbMn2 intermetallic compound. J. Phys. Cond. Matter 1992, 4, 1103–1113.
  29. Ritter, C.; Kilcoyne, S.H.; Cywinski, R. The magnetic structure of DyMn2. J. Phys. Condens. Matter 1991, 3, 727–738.
  30. Ritter, C.; Cywinski, R.; Kilcoyne, S.H.; Mondal, S. The magnetic structure of HoMn2. J. Phys. Condens. Matter 1992, 4, 1559–1566.
  31. Ballou, R.; Brown, P.J.; Deportes, J.; Lemaire, R.; Ouladdiaf, B. Exchange frustration and metastability of the magnetic structure of TbMn2. J. Magn. Magn. Mater. 1992, 104–107, 935–936.
  32. Nakamura, Y.; Shiga, M.; Kawano, S. Antiferromagnetism of YMn2 intermetallic compound. Phys. B+C 1983, 120, 212–215.
  33. Nakamura, H.; Metoki, N.; Suzuki, S.; Takayanagi, F.; Shiga, M. Helimagnetic structure of YMn2 observed by means of nuclear magnetic resonance and neutron diffraction. J. Phys. Condens Matter 2001, 13, 475–500.
  34. Deportes, J.; Ouladdiaf, B.; Ziebeck, K.R.A. Thermal dependence of the longitudinal spin fluctuations in YMn2. J. Physigue 1987, 48, 1029–1034.
  35. Goncharenko, I.N.; Mirebeau, I.; Irodova, A.V.; Suard, E. Magnetic and hydrogen ordering in the frustrated Laves hydrides RMn2 (R = Gd, Tb, Dy, Ho): A neutron-diffraction study. Phys. Rev B 1999, 59, 9324–9331.
  36. Suwarno, S.; Lototskyy, M.V.; Yartys, V.A. Thermal desorption spectroscopy studies of hydrogen desorption from rare earth metal trihydrides REH3 (RE=Dy, Ho, Er). J. Alloys Compd. 2020, 842, 155530.
  37. Charraud, J.-B.; Geneste, G.; Torrent, M. Manganese hydrides and superhydrides at high pressure. Phys. Rev. B 2019, 100, 224102.
  38. Kirchheim, R.; Pundt, A. Hydrogen in Metals. In Physical Metallurgy, 5th ed.; Laughlin, D.E., Hono, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 2597–2705.
  39. Staliński, B.; Terpiłowski, J. Wodór i wodorki; Wydawnictwa Naukowo–Techniczne: Warszawa, Poland, 1987.
  40. Turnbull, A. 4–Hydrogen diffusion and trapping in metals. In Gaseous Hydrogen Embrittlement of Materials in Energy Technologies; Woodhead Publishing: Cambridge, UK, 2012; pp. 89–128.
  41. Fukai, Y. The Metal–Hydrogen System: Basic Bulk Properties; Springer Science+Business Media: Berlin/Heidelberg, Germany, 2006.
  42. Skripov, A.V. Hydrogen jump motion in Laves-phase hydrides: Two frequency scales. J. Alloys Compd. 2005, 404–406, 224–229.
  43. Kehr, K.W. Hydrogen in Metals I–Basic Properties; Alefeld, G., Volkl, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1978.
  44. Graubert, H.; Schrober, H.R. Hydrogen in Metals III—Properties and Applications; Wipf, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1997.
  45. Coey, J.M.D. Interstitial intermetallics. J. Magn. Magn. Mat. 1996, 159, 80–89.
  46. Zuttel, A. Materials for hydrogen storage. Mater. Today 2003, 6, 24–33.
  47. Fujiwara, K. Effect of Hydrogen Absorption on the Magnetic Properties of Pseudobinary Intermetallics Y(Mn1-xTx)2 (T=Al, Co and Ni). J. Phys. Soc. Jpn. 1988, 57, 2133.
  48. Somenkov, V.A.; Irodova, A.V. Lattice structure and phase transitions of hydrogen in intermetallic compounds. J. Less–Common Met. 1984, 101, 481–492.
  49. Figiel, H.; Lindbaum, A.; Kapusta, C.; Gratz, E. Thermal expansion of YMn2Hx compounds. J. Alloys Comp. 1995, 217, 157.
  50. Figiel, H.; Osuchowski, S.; Paja, A. Unit cell expansion in Laves phase-type compounds caused by interstitial hydrogen. Phys. Stat. Sol(A) 2007, 204, 3286–3290.
  51. Budziak, A.; Figiel, H.; Żukrowski, J.; Gratz, E.; Ouladdiaf, B. Magnetic ordering in TbMn2D2. J. Phys. Cond. Matt. 2001, 13, L871.
  52. Switendick, A.C. Band structure calculations for metal hydrogen systems. Z. Phys. Chem. 1979, 117, 89–112.
  53. Westlake, D.G. Hydrides of intermetallic compounds: A review of stabilities, stoichiometries and preferred hydrogen sites. J. Less–Common Met. 1983, 91, 1–20.
  54. Żukrowski, J.; Strecker, M.; Wortmann, G.; Przewoźnik, J.; Krop, K. X-ray diffraction and 155Gd-Mössbauer effect study of GdMn2Hx (0≤ x≤ 4.3). J. Alloys Compd. 1997, 261, 47–53.
  55. Przewoźnik, J.; Żukrowski, J.; Krop, K. Mössbauer effect study of the magnetic ordering in GdMn2Hx. J. Magn. Magn. Mater. 1998, 187, 337–344.
  56. Shoemaker, D.P.; Shoemaker, C.B. Concerning atomic sites and capacities for hydrogen absorption in the AB2 Friauf-Laves phases. J. Less-Common Met. 1979, 68, 43–58.
  57. Wang, C.Y.; Paul-Boncour, V.; Kang, C.C.; Liu, R.S.; Filipek, S.M.; Dorogova, M.; Marchuk, I.; Hirata, T.; Percheron-Guegan, A.; Sheu, H.-S.; et al. The novel YMn2D6 deuteride synthesized under high pressure of gaseous deuterium. Solid State Commun. 2004, 130, 815–820.
  58. Paul-Boncour, V.; Filipek, S.M.; Dorogova, M.; Bouree, F.; Andre, G.; Marchuk, I.; Percheron-Guegan, A.; Liu, R.S. Neutron diffraction study, magnetic properties and thermal stability of YMn2D6 synthesized under high deuterium pressure. J. Sol. State Chem. 2005, 178, 356.
  59. Paul–Boncour, V.; Filipek, S.M.; Andre, G.; Bourée, F.; Guillot, M.; Wierzbicki, R.; Marchuk, I.; Liu, R.S.; Villeroy, B.; Percheron-Guégan, A.; et al. Structural, thermal and magnetic properties of ErMn2D6 synthesized under high deuterium pressure. J. Phys. Condens. Matter 2006, 18, 6409.
  60. Paul–Boncour, V.; Filipek, S.M.; Wierzbicki, R.; Andre, G.; Bouree, F.; Guillot, M. Structural and magnetic properties of DyMn2D6 synthesized under high deuterium pressure. J. Phys. Condens. Matter 2009, 21, 016001.
  61. Figiel, H.; Przewoźnik, J.; Paul–Boncour, V.; Lindbaum, A.; Gratz, E.; Latroche, M.; Escorne, M.; Percheron-Guegan, A.; Mietniowski, P. Hydrogen induced phase transitions in YMn2. J. Alloys Compd. 1998, 274, 29–37.
  62. Przewoźnik, J.; Żukrowski, J.; Friendl, K.; Japa, E.; Krop, K. Magnetic and structural properties of DyMn2Hx (0≤x≤4.2). J. Alloys Comp. 1999, 284, 31–41.
  63. Figiel, H.; Budziak, A.; Zachariasz, P.; Żukrowski, J.; Fisher, G.; Dormann, E. Hydrogen induced structural and magnetic transformations in the hexagonal Laves phase ErMn2. J. Alloys Comp. 2004, 368, 260–268.
  64. Budziak, A.; Zachariasz, P.; Pełka, R.; Figiel, H.; Żukrowski, J.; Woch, M.W. Structural and magnetic transformations in NdMn2Hx hydrides. J. Alloys Comp. 2012, 525, 175–183.
  65. Budziak, A.; Zachariasz, P.; Kolwicz-Chodak, L.; Figiel, H.; Pacyna, A.; Żukrowski, J. Structural and magnetic properties of C15 HoMn2 hydrides. J. Alloys Comp. 2011, 509, 1347–1354.
  66. Maehlen, J.P.; Yartys, V.A.; Riabov, A.B.; Budziak, A.; Figiel, H.; Żukrowski, J. Synchrotron X-ray diffraction study of ErMn2D2. J. Alloys Comp. 2007, 437, 140–145.
  67. Makihara, Y.; Iwata, Y.; Umeda, K.; Miyairi, Y.; Fujii, H. Structural and Hydriding/Dehydriding Properties of HoMn2Hx with Cubic and Hexagonal Laves Phase Structure. MRS Online Proc. Libr. (OPL) 2006, 927, 0927-EE03.
  68. Hirata, T.; Dorogowa, M.; Filipek, S. The hydrogen concentration dependence of the unit-cell volume in RMn2Hx (R = Y.; Gd, Tb and Dy). Phys. Stat. Sol(A) 2004, 201, 1458–1462.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback