Active SLAM: A Review On Last Decade: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Jason Zhu and Version 1 by Muhammad Farhan Ahmed.

This aHerticle presents a comprehensive review of Active Simultaneous Localization and Mapping (A-SLAM) research conducted over the past decade. It explores the formulation, applications, and methodologies employed in A-SLAM, particularly in trajectory generation and control action selection, drawing on concepts from Information Theory (IT) and the Theory of Optimal Experimental Design (TOED). The reviewentry includes both qualitative and quantitative analyses of various approaches, deployment scenarios, configurations, path planning methods, and utility functions within A-SLAM research. Furthermore, this article introduces a novel analysis of Active Collaborative SLAM (AC-SLAM), focusing on collaborative aspects within SLAM systems. It includes a thorough examination of collaborative parameters and approaches, supported by both qualitative and statistical assessments. The study also identifies limitations in the existing literature and suggests potential avenues for future research. This survey serves as a valuable resource for researchers seeking insights into A-SLAM methods and techniques, offering a current overview of A-SLAM formulation.

  • SLAM
  • active SLAM
  • information theory

1. Introduction

As described earlier, SLAM is a process in which a robot maps its environment and localizes itself to it. Referring to Figure 1, in SLAM, the front end handles perception tasks, which involve implementing methods in signal processing and computer-vision domains to compute the estimated relative pose of the robot and the landmarks (observed features). Data from the sensors, which are typically Light Detection and Ranging (Lidar), camera, and Inertial Measurement Unit (IMU) data, are processed by the front-end module, which computes feature extraction, data association, and feature classification and applies methods such as Iterative Closest Point (ICP) and loop closure to compute the estimated robot and landmarks pose with respect to the environment. The ICP is an iterative approach that computes the relative robot pose/transformation that optimizes/aligns the features and is used in scan-matching methods to map the environment. The back-end module is responsible for high-computational tasks involving Bundle Adjustment (B.A) and pose-graph optimization by using iterative solvers, e.g., Gauss–Newton [1] or Levenberg–Marquardt [2] algorithms, to solve the nonlinear optimization problem for an optimal estimate of the state vector 𝑥∗, as shown in Equation (1). The back-end module outputs the global map based on its sensor measurements by using Lidar/a camera and pose estimates of both the robot and landmarks.
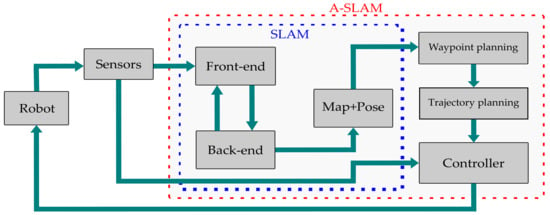
Sensors 23 08097 g001
Figure 1.
Architecture of SLAM and A-SLAM.
A-SLAM deals with designing robot trajectories to minimize the uncertainty in the map representation and localization of the robot. The aim is to perform autonomous navigation and exploration of the environment without an external controller or human effort. A-SLAM can be referred to as an additional module or super set of SLAM systems that incorporates waypoints and trajectory planning and controller modules by using Information Theory (IT), control theory, and Reinforcement Learning (RL) methods to autonomously guide the robot toward its goal. During waypoint planning, A-SLAM chooses obstacle-free waypoints/points for suitable trajectory. Trajectory planning integrates these points with time and generates a trajectory for the robot to follow. The controller sends actuator commands to the robot to follow the desired trajectory and reach the goal position.

2. A-SLAM Formulation

A-SLAM is formulated in a scenario where the robot has to navigate in a partially observable/unknown environment by selecting a series of future actions in the presence of noisy sensor measurements that reduce its state and map uncertainties with respect to the environment. Such a scenario can be modeled as an instance of the Partially Observable Markov Decision Process (POMDP), as discussed in [3][4][5]. The POMDP is defined as a seven tuple (𝑋,𝐴,𝑂,𝑇,𝜌𝑜,𝛽,𝛾)

, where 𝑋∈ℝ represents the robot state space and is represented as the current state 𝑥∈𝑋 and the next state 𝑥′∈𝑋; 𝐴∈ℝ is the action space and can be expressed as 𝑎∈𝐴; O represents the observations where 𝑜∈𝑂; T is the state-transition function between an action (a), present state (x), and next state (𝑥′); T accounts for the robot control uncertainty in reaching the new state 𝑥′; 𝜌𝑜 accounts for sensing uncertainty; 𝛽 is the reward associated with the action taken in state x; and 𝛾∈(0,1) takes into account the discount factor ensuring a finite reward even if the planning task has an infinite horizon. Both T and 𝜌𝑜 can be expressed by using conditional probabilities as Equations (2) and (3):

𝑇(𝑥,𝑎,𝑥′)=𝑝(𝑥′∣𝑥,𝑎)
𝜌𝑜(𝑥,𝑎,𝑜)=𝑝(𝑜∣𝑥′,𝑎)
Researchers can consider a scenario where the robot is in state x and takes an action a to move to 𝑥’. This action uncertainty is modeled by T with an associated reward modeled by 𝛽, and then it takes an observation o from its sensors that may not be precise in their measurements, and this sensor uncertainty is modeled by 𝜌𝑜. The robot’s goal is to choose the optimal policy 𝛼∗ that maximizes the associated expected reward (𝔼) for each state–action pair, and it can be modeled as Equation (4):
𝛼∗=argmax𝑡∑𝑡=0∞𝔼𝛾𝑡𝛽(𝑥𝑡,𝑎𝑡)

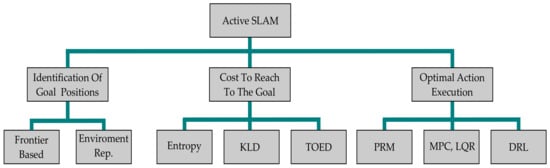
where 𝑥𝑡, 𝑎𝑡, and 𝛾𝑡 are the state, action, and discount factor evolution at time t, respectively. Although the POMDP formulation of A-SLAM is the most widely used approach, it is considered computationally expensive as it considers planning and decision making under uncertainty. For computational convenience, A-SLAM formulation is divided into three main submodules which identify the potential goal positions/waypoints, compute the cost to reach them, and then select actions based on utility criterion, which decreases the map uncertainty and increases the robot’s localization.

3. A-SLAM Components

To deal with the computational complexity of A-SLAM, it is divided into three main submodules, as depicted in Figure 2. The robot initially identifies potential goal positions to explore or exploit its current estimate of the map. The map represents the environment perceived by the robot by using its onboard sensors, and it may be classified as (1) topological maps, which use a graphical representation of the environment and provide a simplified topological representation; (2) metric maps, which provide environment information in the form of a sparse set of information points (landmarks) or full 3D representation of the environment (point cloud); and (3) semantic maps, which provide only segmented information about environment objects (like static obstacles) to the robot. Interested readers are directed to [6][7] for a detailed discussion on mapping approaches. Once the robot has a map of its environment by using any of the above approaches, it searches for potential target/goal locations to explore. One of the most widely used methods is frontier-based exploration initially used by [8], where the frontier is the border between the known and unknown map locations. Figure 3 shows frontiers detected by using Lidar measurements on the occupancy grid map in a simulation environment. Using frontier-based exploration has the advantage that all the environment may be covered, but no exploitation task (revisiting already-visited areas for loop closure) is performed, which affects the robot’s map estimate.
Sensors 23 08097 g002
Figure 2.
A-SLAM submodules.
Sensors 23 08097 g003
Figure 3. (a) AWS-simulated house environment: red= robot and blue = Lidar scans. (b) Frontier detection on the occupancy grid map: red = robot, green = detected frontiers (centroids), white = free space, gray = unknown map area, and black = obstacles [9].
Once the goal position is identified, the next step is to compute the cost or utility function to that position based on the reward value of the optimal action selected from a set of all possible actions according to Equation (4). Ideally, this utility function should consider a full joint-probability distribution of map and robot poses, but this method is computationally expensive. Since Researchers have a probabilistic estimation of both the robot and map, Researchers can treat them as random variables with associated uncertainty in their estimation. The two most common approaches used in the quantification of this uncertainty are Information Theory (IT), initially coined by Shannon in 1949, and the Theory of Optimal Experimental Design (TOED) [10].
In IT, entropy measures the amount of uncertainty associated with a random variable or random quantity. Higher entropy leads to less information gain and vice versa. Formally, it is defined for a random variable X as ℋ(𝑋), as shown in Equation (5):
ℋ(𝑋)=−∑𝑥∈𝑋𝑝(𝑥)log2𝑝(𝑥)
Since both the robot pose and the map are estimated as a multivariate Gaussian, the authors of [11] formulate the Shannon’s entropy of the robot pose as in Equation (6), where n is the dimension of the robot pose vector and Ω∈ℝ𝑛𝑥𝑛

is the covariance matrix. The map entropy is defined as Equation (7), where the map M is represented as an occupancy grid and each cell 𝑚𝑖,𝑗 is associated with a Bernoulli distribution 𝑃(𝑚𝑖,𝑗). The objective is to reduce both the robot pose and map entropy. Relative entropy is also be used as a utility function that measures the probability distribution along with its deviation from its mean. This relative entropy is measured as the Kullback–Leibler divergence (KLD). The KLD for two discrete distributions A and B on probability space X can be defined as Equation (8):

ℋ[𝑝(𝑥)]=𝑛2(1+log(2𝜋)+12log(𝑑𝑒𝑡Ω)
ℋ[𝑝(𝑀)]=−∑𝑖,𝑗(𝑝(𝑚𝑖,𝑗)𝑙𝑜𝑔(𝑝(𝑚𝑖,𝑗))+(1−𝑝(𝑚𝑖,𝑗))𝑙𝑜𝑔(1−𝑝(𝑚𝑖,𝑗))
𝒟𝐾𝐿(𝐴∣𝐵)=∑𝑥∈𝑋𝐴(𝑥)log𝐴(𝑥)𝐵(𝑥)
When considering information-driven utility functions, entropy or KLD can be used as a metric to target binary probabilities in the grid map (occupancy grid map). Alternatively, if Researchers consider task-driven utility functions where the uncertainty metric is evaluated by reasoning over the propagation of uncertainty in the pose-graph SLAM covariance matrix, Researchers can quantify the uncertainty in the task space. TOED provides many optimal criteria, which transform the mapping of the covariance matrix to a scalar value. Hence, by using TOED, the priority of a set of actions for A-SLAM is based on the amount of covariance in the joint posterior. Less covariance contributes to a higher weight of the action set. The “optimality criterion” used in TOED can be defined for a covariance matrix Ω∈ℝ𝑛𝑥𝑛 and eigenvalues 𝜁𝑛 as (1) A-optimality, which deals with the minimization of the average variance, as shown in Equation (9); (2) D-optimality, which deals with minimizing the volume of the covariance ellipsoid and is defined in Equation (10); and (3) E-optimality, which intends to minimize the maximum eigenvalue and is expressed in Equation (11):
𝐴−𝑂𝑝𝑡=Δ1𝑛(∑𝑘=1𝑛𝜁𝑘)
𝐷−𝑂𝑝𝑡=Δ𝑒𝑥𝑝(1𝑛∑𝑘=1𝑛𝑙𝑜𝑔(𝜁𝑘))
𝐸−𝑂𝑝𝑡=Δ𝑚𝑖𝑛1≤𝑖≤𝑛(𝜁𝑖)
TOED approaches require both the robot pose and map uncertainties to be represented as a covariance matrix and may be computationally expensive, especially in landmark-based SLAM where its size increases as new landmarks are discovered. Hence, IT-based approaches are preferred over TOED.
Once the goal positions and utility/cost to reach these positions have been identified, the next step is to execute the optimal action, which eventually moves/guides the robot to the goal position. Three approaches are commonly deployed:
  • Probabilistic Road Map (PRM) approaches discretize the environment representation and formulate a network graph representing the possible paths for the robot to select to reach the goal position. These approaches work in a heuristic manner and may not give the optimal path; additionally, the robot model is not incorporated in the planning phase, which may result in unexpected movements. Rapidly exploring Random Trees (RRT) [12], D* [13], and A* [14] are the widely used PRM methods.
  • Linear Quadratic Regulator (LQR) and Model Predictive Control (MPC) formulate the robot path-planning problem as an Optimal Control Problem (OCP) and are used to compute the robot trajectory over a finite time horizon in a continuous-planning domain. Consider a robot with the state-transition equation given by 𝑥(𝑘+1)=𝑓(𝑥(𝑘),𝑢(𝑘))

, where x, u, and k are the state, control, and time, respectively. The MPC controller finds the optimal control action 𝑢∗(𝑥(𝑘)) for a finite horizon N, as shown in Equation (12), which minimizes the relative error between the desired state 𝑥𝑟 and desired control effort 𝑢𝑟, weighted by matrices Q and P for the penalization of state and control errors, respectively, as shown in Equation (13). The MPC is formulated as minimizing the objective function 𝐽𝑁 as defined in (14), which takes into account the costs related to control effort and robot state evolution over the entire prediction horizon. MPC provides an optimal trajectory incorporating the robot state model and control and state constraints, making it suitable for path planning in dynamic environments:

𝑢∗(𝑥(𝑘)):=(𝑢∗(𝑘),𝑢∗(𝑘+1),....𝑢∗(𝑘+𝑁−1),)
𝑙(𝑥,𝑢)=∥𝑥𝑢−𝑥𝑟∥2𝑄+∥𝑢−𝑢𝑟∥2𝑅
minimize𝑢𝐽𝑁(𝑥0,𝑢)=∑𝑘=0𝑁−1𝑙((𝑥𝑢(𝑘),𝑢(𝑘)))
Reinforcement Learning (RL) is modeled as a Markov Decision Process (MDP) where an agent at state s interacts with the environment by performing an action a and receiving a reward r. The objective is to find a good policy 𝜋(𝑠,𝑎) which maximizes the aggregation of the rewards in the long run following a value function 𝑉𝜋(𝑠𝑡0), as shown in Equation (15), that maximizes the expected reward attained by the agent, weighted by the discount factor 𝛾𝑡∈[0,1]. In the case of visual A-SLAM, the policy may be to move the robot to more feature-rich positions to maximize the reward (observed features). Deep Reinforcement Learning (DRL) replaces the agent with a deep neural network that parameterizes the policy 𝜋 with some weighting parameter 𝜃 and is given as 𝜋𝜃(𝑠,𝑎) to maximize the future rewards of each state–action pair during the evolution of the robot trajectory. Researchers will further discuss the application of these approaches in Section 2.4:
𝑉𝜋(𝑠𝑡0)=∑𝑡=𝑡0∞𝛾𝑡𝑟(𝑠𝑡,𝜋(𝑠𝑡,𝑎𝑡))
The choice of selecting a suitable waypoint candidate is weighted by using IT and TOED, as discussed in previous sections. In these methods, information gain or entropy minimization between the map and robot path guides the decision for the selection of these future waypoint candidates. To generate a trajectory or a set of actions for these future waypoint candidates, two main methods are adopted, namely geometric and dynamic approaches, respectively. These methods involve the usage of traditional path planners along with the DRL and nonlinear optimal control techniques.

4. Geometric Approaches

These methods describe A-SLAM as a task for the robot whereby it must choose the optimal path and trajectory while reducing its poses and mapping uncertainty for efficient SLAM to autonomously navigate an unknown environment. The exploration space is discretized with finite random waypoints and frontier-based exploration along with traditional path planners like RRT*, D*, and A*, which are deployed with IT- and TOED-based approaches including entropy, KLD, and uncertainty metrics reduction.

4.1. IT-Based Approaches

The authors of [15] address the joint-entropy minimization exploration problem and propose two modified versions of RRT* [12] called dRRT* and eRRT*. dRRT* uses distance, while eRRT* uses entropy change per distance traveled as the cost function. It is further debated that map entropy has a strong relationship with coverage and path entropy has a relationship with map quality (as better localization produces a better map). Hence, actions are computed in terms of the joint-entropy change per distance traveled. The simulation results proved that a combination of both of these approaches provides the best path-planning strategy. An interesting comparison between IT approaches is given in [16], where particle filters are used as the back end of A-SLAM and frontier-based exploration (a frontier is a boundary between the visited and unexplored areas) [8] is deployed to select future candidate target positions. A comparison of these three methods used for solving the exploration problem and evaluating the information is discussed in the relevant sections below:
  • Joint entropy: The information gained at the target is evaluated by using the entropy of both the robot trajectory and map carried by each particle weighted by each trajectory’s importance weight. The best exploration target is selected, which maximizes the joint-entropy reduction and hence corresponds to higher information gain.
  • Expected Map Mean: An expected mean can be defined as the mathematical expectation of the map hypotheses of a particle set. The expected map mean can be applied to detect already-traversed loops on the map. Since the computation of the gain is developing, the complexity of this method increases.
  • Expected information from a policy: Kullback–Leibler divergence [17] is used to drive an upper bound on the divergence between the true posterior and the approximated pose belief. Apart from the information consistency of the particle filter, this method also considers the information loss due to inconsistent mapping.
It was concluded by using simulation results on various datasets, that most of these approaches were not able to properly address the probabilistic aspects of the problem and are most likely to fail because of a high computational cost and the map-grid resolution dependency on performance.
The authors of [18] use an exploration space represented by primitive geometric shapes, and an entropy reduction over the map features is computed. They use an entropy metric based on Laplacian approximation and compute a unified quantification of exploration and exploitation gains. An efficient sampling-based path planner is used based on a Probabilistic Road Map approach, having a cost function that reduces the control cost (distance) and collision penalty between targets. The simulation results compared to the traditional grid-map frontier exploration show a significant reduction in position, orientation, and exploration errors. Future improvements include expanding to an active visual SLAM framework.

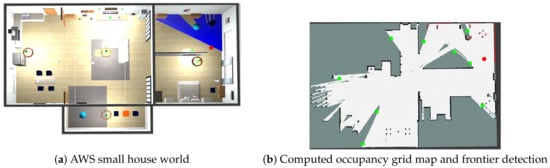
4.2. Frontier-Based Exploration

Frontiers are boundaries between the explored and unexplored space. Formally, Researchers can describe frontiers as a set of unknown points that each have at least one known space neighbor. The work presented by [19] formulates a hybrid control-switching exploration method of particle filter SLAM as the back end. It uses a frontier-based exploration method with A* [14] as a global planner and the Dynamic Window Approach (DWA) reactive algorithm as a local planner. Within the occupancy grid map, each frontier is segmented, a trajectory is planned for each segment, and the trajectory with the highest map-segment covariance is selected from the global-cost map. The work presented in [20] deals with dynamic environments with multiple ground robots and uses frontier exploration for autonomous exploration with graph-based SLAM (iSAM) [21] optimization as the SLAM back end. Dijkstra’s algorithm-based local planner is used. Finally, a utility function based on Shannon’s and Renyi entropy is used for the computation of the utility of paths. Future work proposes to integrate a camera and use image-feature scan matching for obstacle avoidance.

4.3. Path-Planning Optimization

The method proposed by [22] exploits the relationship between the graphical model and sparse matrix factorization of graphical SLAM. It proposes the ordering of variables and a subtree-catching scheme to facilitate the fast computation of optimized candidate paths weighted by the belief changes between them. The horizon selection criteria are based on the author’s previous work utilizing an extended information filter (EIF) and Gauss–Newton (GN) prediction. The proposed solution is implemented in a Hovering Autonomous Underwater Vehicle (HAUV) with pose-graph SLAM. The work presented in [23] deals with a similar volumetric exploration in an underwater environment with a multibeam sonar. For efficient path planning, the revisit actions are selected depending on the pose uncertainty and sensor-information gain.
The authors of [24] used an interesting approach that addresses the path-planning task as D* [13] with negative edge weights to compute the shortest path in the case of a change in localization. This exploration method is highly effective in dynamic environments with changing obstacles and localization. When dealing with noisy sensor measurements, an interesting approach is adopted by [25], which proposes a system that makes use of a multihypothesis state and map estimates based on noisy or insufficient sensor information. This method uses the local contours for efficient multihypothesis path planning and incorporates loop closure.

4.4. Optimization in Robot Trajectory

The method proposed in [26] integrates A-SLAM with Ekman’s exploration algorithm [27] to optimize the robot trajectory by leveraging only the global waypoints where loop closure appears, and then the exploration canceling criterion is sent to the SLAM back end (based on the information filter [28]). The exploration canceling criterion depends on the magnitude of information gain from the filter, loop-closure detection, and the number of states without an update. If these criteria are met, the A-SLAM causes the exploration algorithm to stop and guides the robot to close the loop. Researchers must note that in this approach, A-SLAM is separated from the route-planning and -exploration process, which is managed by the information filter. Then, A-SLAM exploits this map information for active loop closure. The proposed method calculates an optimal global plan as a solution to the Chinese Postman Problem (CPP) [29] and an online algorithm that computes the maximum likelihood estimate (MLE) by using nonlinear optimization, which computes the optimized graph with respect to the prior map and explored map. The D-optimality criterion is used to represent the robot localization uncertainty while the work presented by [30] incorporates active path planning with salient features (features with a high entropy value) and ICP-based feature matching [31]. The triggering condition of A-SLAM is based on an active feature revisit, and the path with the maximum utility score is chosen based on its length and map data.

4.5. Optimal Policy Selection

The definition and comparison presented in [32] formulate A-SLAM as a task of choosing a single or multiple policy type for robot trajectories, which minimizes an objective function that comprises a reduction in the expected costs of robot uncertainty, energy consumption, and navigation time among other factors. An optimality criterion by definition quantifies the improvement in the actions taken by the robot to improve the localization accuracy and navigation time. A comparison between D-optimality (proportional to the determinant of the covariance matrix), A-optimality (proportional to the trace of the covariance matrix), and joint entropy is performed, and it is concluded that the D-optimality criterion is more appropriate for providing useful information about the robot’s uncertainty contrary to A-optimality. The authors of [33] proved numerically that by using differential representations to propagate the spacial uncertainty, monotonicity is preserved for all the optimality criteria A-opt, D-opt, and E-opt (the largest eigenvalue of the covariance matrix). In absolute representations using only unit quaternions, the monotonicity is preserved only in D-optimality and Shannon’s entropy. In a similar comparison, the work presented in [34] concludes that A-Opt and E-opt criteria do not hold monotonicity in dead reckoning scenarios. It is proved by using simulations with a differential drive robot that the D-opt criterion, under a linearized odometry method, holds monotonicity.

5. Dynamic Approaches

Instead of using traditional path planners like A*, D*, and RRT, these methods formulate the A-SLAM as a problem with selecting a series of control inputs to generate a collision-free trajectory and cover as much area as possible while minimizing the state-estimation uncertainty and thus improve the localization and mapping of the environment. The planning and action spaces are now continuous (contrary to being discrete in geometry-based methods) and local optimal trajectories are computed. For the selection of optimal goal positions, similar approaches to the geometric approach methods in Section 2.3 are used with the exception that now the future candidate trajectories are computed by using robot models, potential information fields, and control theory. A Linear Quadratic Regulator (LQR), Model Predictive Control (MPC) [35], the Markov Decision Process [36], or Reinforcement Learning (RL) [37] are used to choose the optimal future trajectories/set of trajectories via metrics that balance the need for exploring new areas and exploiting already-visited areas for loop closure.
The method used by [38] uses Reinforcement Learning in the path planner to acquire a vehicle model by incorporating a 3D controller. The 3D controller can be simplified to one 2D controller for forward and backward motion and one 1D controller for path planning that has an objective function that maximizes the map reliability and exploration zone. Therefore, the planner has an objective function that maximizes the accumulated reward for each state–action pair by using the “learning from experience approach”. It is shown through simulations that a nonholonomic vehicle learns the virtual wall-following behavior. A similar approach presented in [39] uses fully convolutional residual networks to recognize the obstacles and obtain a depth image. The path-planning algorithm is based on DRL.
An active localization solution where only the rotational movement of the robot is controlled in a position-tracking problem is presented by [40]. The Adaptive Monte Carlo Localization (AMCL) particle cloud is used as the input, and robot-control commands are sent to its sensors as the output. The proposed solution involves the spectral clustering of the point cloud, building a compound map from each particle cluster, and selecting the most informative cell. The active localization is triggered when the robot has more than one cluster in its uncertainty estimate. The future improvements include more cells for efficient hypotheses estimation and integrating this approach into the SLAM front end. In an interesting approach by [41], the saccade movement of bionic eyes (rapid movement of the center of one’s gaze within the visual field) is controlled. To leverage more features from the environment, an autonomous control strategy inspired by the human vision system is incorporated. The A-SLAM system involves two threads (parallel processes), a control thread, and a tracking thread. The control thread controls the bionic eyes’ movement to Oriented FAST and Rotated Brief (ORB) feature-rich positions while the tracking thread tracks the eye motion by selecting the feature-rich keyframes.

6. Hybrid Approaches

These methods use the geometry and dynamic-based methods mentioned in Section 2.3 and Section 2.4 incorporating frontier-based exploration, Information Theory, and Model Predictive Control (MPC) to solve the A-SLAM problem.
The approach used by the authors of [42] presents an open-source multilayer A-SLAM approach where the first layer selects the informative (utility criterion based on Shannon’s entropy [43]) goal locations (frontier points) and generates paths to these locations while the second and third layers actively replan the path based on the updated occupancy grid map. Nonlinear MPC [44] is applied for local path execution with the objective function based on minimizing the distance to the target and controlling the effort and cost of being close to a nearby obstacle. One issue with this approach is that sometimes the robot stops and starts the replanning phase of local paths. Future works should involve adding dynamic obstacles and the usage of aerial robots.
An interesting approach mentioned in [45][46] presents a solution based on Model Predictive Control (MPC) to solve the area coverage and uncertainty reduction in A-SLAM. An MPC control-switching mechanism is formulated, and SLAM uncertainty reduction is treated as a graph topology problem and planned as a constrained nonlinear least-squares problem. Using convex relaxation, the SLAM uncertainty is reduced by a convex optimization method. The area-coverage task is solved via the sequential quadratic programming method, and Linear SLAM is used for submap joining.

7. Reasoning over Spectral Graph Connectivity

Recently, in the works of [47][48], the authors exploit the graph SLAM connectivity and pose it as an estimation-over-graph (EoG) problem, where each node (state vector) and the vertex (measurement) connectivity is strongly related to the SLAM estimation reliability. By exploiting the spectral graph theory, which deals with the eigenvalues, Laplacian, and degree matrix of the associated SLAM information matrix and graph connectivity, the authors state that (1) the graph Laplacian is related to the SLAM information matrix and (2) the number of Weighted Spanning Trees (WST) is directly related to the estimation accuracy of the graph SLAM.
The authors of [49][50][51] extend [48] by debating that the maximum number of WST is directly related to the maximum likelihood (ML) estimate of the underlying graph SLAM problem formulated over lie algebra [52]. Instead of computing the D-optimality criterion defined in Equation (10) over the entire SLAM sparse-information matrix, it is computed over the weighted graph Laplacian where each vertex is weighted by using D-optimality, and it is proven that the maximum number of WST of this weighted graph Laplacian is directly related to the underlying pose-graph uncertainty.
Real robot experiments on both the Lidar and visual SLAM backbends prove the efficiency and robustness of reasoning the uncertainty over the SLAM-graph connectivity.

References

  1. Gratton, S.; Lawless, A.S.; Nichols, N.K. Approximate Gauss–Newton Methods for Nonlinear Least Squares Problems. SIAM J. Optim. 2007, 18, 106–132.
  2. Watson, G.A. Lecture Notes in Mathematics. In Proceedings of the 7th Dundee Biennial Conference on Numerical Analysis, Dundee, UK, 28 June–1 July 1977; Springer: Berlin/Heidelberg, Germany, 1978. ISBN 978-3-540-08538-6.
  3. Placed, J.A.; Strader, J.; Carrillo, H.; Atanasov, N.; Indelman, V.; Carlone, L.; Castellanos, J.A. A survey on active simultaneous localization and mapping: State of the art and new frontiers. IEEE Trans. Robot. 2023, 39, 1686–1705.
  4. Fox, D.; Burgard, W.; Thrun, S. Active Markov Localization for Mobile Robots. Robot. Auton. Syst. 1998, 25, 195–207.
  5. Placed, J.A.; Castellanos, J.A. A Deep Reinforcement Learning Approach for Active SLAM. Appl. Sci. 2020, 10, 8386.
  6. Dhiman, N.K.; Deodhare, D.; Khemani, D. Where Am I? Creating Spatial Awareness in Unmanned Ground Robots Using SLAM: A Survey. Sadhana 2015, 40, 1385–1433.
  7. Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332.
  8. Yamauchi, B. A frontier-based approach for autonomous exploration. In Proceedings of the 1997 IEEE International Symposium on Computational Intelligence in Robotics and Automation CIRA’97, ‘Towards New Computational Principles for Robotics and Automation’, Monterey, CA, USA, 10–11 July 1997; pp. 146–151.
  9. Available online: https://github.com/aws-robotics/aws-robomaker-small-house-world (accessed on 10 January 2023).
  10. Pázman, A. Foundations of Optimum Experimantal Design; Springer: Berlin/Heidelberg, Germany, 1996; Volume 14.
  11. Stachniss, C.; Grisetti, G.; Burgard, W. Information Gain-Based Exploration Using Rao-Blackwellized Particle Filters. In Proceedings of the Robotics: Science and Systems I, Massachusetts Institute of Technology, Cambridge, MA, USA, 8 June 2005; pp. 65–72.
  12. Naderi, K.; Rajamäki, J.; Hämäläinen, P. RT-RRT*: A real-time path planning algorithm based on RRT*. In Proceedings of the 8th ACM SIGGRAPH Conference on Motion in Games, Paris, France, 16–18 November 2015; pp. 113–118.
  13. Stentz, A. The D* Algorithm for Real-Time Planning of Optimal Traverses; Technical Report; CMU-RI-TR-94-37; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 1994.
  14. Liu, X.; Gong, D. A comparative study of A-star algorithms for search and rescue in perfect maze. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011.
  15. Vallve, J.; Andrade-Cetto, J. Active pose slam with RRT. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015.
  16. Du, J.; Carlone, L.; Kaouk, N.M.; Bona, B.; Indri, M. A comparative study on A-SLAM and autonomous exploration with particle filters. In Proceedings of the 2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Budapest, Hungary, 3–7 July 2011; pp. 916–923.
  17. Carlone, L.; Du, J.; Kaouk, N.M.; Bona, B.; Indri, M. A-SLAM and exploration with particle filters using Kullback-Leibler divergence. J. Intell. Robot. Syst. 2013, 75, 291–311.
  18. Mu, B.; Giamou, M.; Paull, L.; Agha-Mohammadi, A.; Leonard, J.; How, J. Information-based A-SLAM via topological feature graphs. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016.
  19. Trivun, D.; Salaka, E.; Osmankovic, D.; Velagic, J.; Osmic, N. A-SLAM-based algorithm for autonomous exploration with Mobile Robot. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015.
  20. Mammolo, D. A-SLAM in Crowded Environments. Master’s Thesis, Autonomous Systems Lab, ETH Zurich, Zurich, Switzerland, 2019.
  21. Kaess, M.; Ranganathan, A.; Dellaert, F. ISAM: Incremental Smoothing and Mapping. IEEE Trans. Robot. 2008, 24, 1365–1378.
  22. Chaves, S.M.; Eustice, R.M. Efficient planning with the Bayes Tree for A-SLAM. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016.
  23. Suresh, S.; Sodhi, P.; Mangelson, J.G.; Wettergreen, D.; Kaess, M. A-SLAM using 3D SUBMAP saliency for underwater volumetric exploration. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020.
  24. Maurovic, I.; Seder, M.; Lenac, K.; Petrovic, I. Path Planning for Active SLAM Based on the D* Algorithm with Negative Edge Weights. IEEE Trans. Syst. Man Cybern Syst. 2018, 48, 1321–1331.
  25. Hsiao, M.; Mangelson, J.G.; Suresh, S.; Debrunner, C.; Kaess, M. ARAS: Ambiguity-aware robust A-SLAM based on multi-hypothesis state and map estimations. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021.
  26. Lenac, K.; Kitanov, A.; Maurović, I.; Dakulović, M.; Petrović, I. Fast Active SLAM for Accurate and Complete Coverage Mapping of Unknown Environments. In Intelligent Autonomous Systems 13; Menegatti, E., Michael, N., Berns, K., Yamaguchi, H., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2016; Volume 302, pp. 415–428. ISBN 978-3-319-08337-7.
  27. Ekman, A.; Torne, A.; Stromberg, D. Exploration of polygonal environments using range data. IEEE Trans. Syst. Man, Cybern. Part B 1997, 27, 250–255.
  28. Eustice, R.M.; Singh, H.; Leonard, J.J. Exactly Sparse Delayed-State Filters for View-Based SLAM. IEEE Trans. Robot. 2006, 22, 1100–1114.
  29. Sökmen, Ö.; Emeç, Ş.; Yilmaz, M.; Akkaya, G. An Overview of Chinese Postman Problem. In Proceedings of the 3rd International Conference on Advanced Engineering Technologies, Turkey, 19–20 September 2019.
  30. Li, G.; Geng, Y.; Zhang, W. Autonomous Planetary Rover Navigation via A-SLAM. Aircr. Eng. Aerosp. Technol. 2018, 91, 60–68.
  31. He, Y.; Liang, B.; Yang, J.; Li, S.; He, J. An iterative closest points algorithm for registration of 3D laser scanner point clouds with geometric features. Sensors 2017, 17, 1862.
  32. Carrillo, H.; Reid, I.; Castellanos, J.A. On the comparison of uncertainty criteria for A-SLAM. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012.
  33. Rodriguez-Arevalo, M.L.; Neira, J.; Castellanos, J.A. On the importance of uncertainty representation in A-SLAM. IEEE Trans. Robot. 2018, 34, 829–834.
  34. Carrillo, H.; Latif, Y.; Rodriguez-Arevalo, M.L.; Neira, J.; Castellanos, J.A. On the Monotonicity of optimality criteria during exploration in A-SLAM. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015.
  35. Bemporad, A. Model predictive control design: New trends and tools. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 6678–6683.
  36. Jayaweera, S.K. Markov decision processes. In Signal Processing for Cognitive Radios; Wiley: Hoboken, NJ, USA, 2015; pp. 207–268.
  37. Qiang, W.; Zhongli, Z. Reinforcement learning model, algorithms and its application. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 1143–1146.
  38. Martinez-Marin, T.; Lopez, E.; De Bernardis, C. An unified framework for A-SLAM and Online Optimal Motion Planning. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011.
  39. Wen, S.; Zhao, Y.; Yuan, X.; Wang, Z.; Zhang, D.; Manfredi, L. Path planning for A-SLAM based on deep reinforcement learning under unknown environments. Intell. Serv. Robot. 2020, 13, 263–272.
  40. Andrade, F.; LLofriu, M.; Tanco, M.M.; Barnech, G.T.; Tejera, G. Active localization for mobile service robots in symmetrical and Open Environments. In Proceedings of the 2021 Latin American Robotics Symposium (LARS), 2021 Brazilian Symposium on Robotics (SBR), and 2021 Workshop on Robotics in Education (WRE), Natal, Brazil, 11–15 October 2021.
  41. Liu, Y.; Zhu, D.; Peng, J.; Wang, X.; Wang, L.; Chen, L.; Li, J.; Zhang, X. Robust active visual slam system based on Bionic Eyes. In Proceedings of the 2019 IEEE International Conference on Cyborg and Bionic Systems (CBS), Munich, Germany, 18–20 September 2019.
  42. Bonetto, E.; Goldschmid, P.; Pabst, M.; Black, M.J.; Ahmad, A. iRotate: Active visual slam for Omnidirectional Robots. Robot. Auton. Syst. 2022, 154, 104102.
  43. Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656.
  44. Findeisen, R.; Allgöwer, F. An introduction to nonlinear model predictive control. In Proceedings of the 21st Benelux Meeting on Systems and Control, Veldhoven, The Netherlands, 19–21 March 2002.
  45. Chen, Y.; Huang, S.; Fitch, R. A-SLAM for mobile robots with area coverage and obstacle avoidance. IEEE/ASME Trans. Mechatronics 2020, 25, 1182–1192.
  46. Chen, Y.; Huang, S.; Fitch, R.; Yu, J. Efficient A-SLAM based on submap joining, graph topology and convex optimization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018.
  47. Khosoussi, K.; Sukhatme, G.S.; Huang, S.; Dissanayake, G. Maximizing the Weighted Number of Spanning Trees: Near-t-Optimal Graphs. arXiv 2016, arXiv:1604.01116.
  48. Khosoussi, K.; Giamou, M.; Sukhatme, G.S.; Huang, S.; Dissanayake, G.; How, J.P. Reliable Graphs for SLAM. Int. J. Robot. Res. 2019, 38, 260–298.
  49. Placed, J.A.; Castellanos, J.A. A General Relationship Between Optimality Criteria and Connectivity Indices for Active Graph-SLAM. IEEE Robot. Autom. Lett. 2023, 8, 816–823.
  50. Placed, J.A.; Rodríguez, J.J.G.; Tardós, J.D.; Castellanos, J.A. ExplORB-SLAM: Active Visual SLAM Exploiting the Pose-graph Topology. In Proceedings of the Fifth Iberian Robotics Conference. ROBOT 2022. Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 589.
  51. Placed, J.A.; Castellanos, J.A. Fast Autonomous Robotic Exploration Using the Underlying Graph Structure. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September 2021; pp. 6672–6679.
  52. Deray, J.; Solà, J. Manif: A micro Lie theory library for state estimation in robotics applications. J. Open Source Softw. 2020, 5, 1371.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback