Deep Learning for Motor Imagery Brain–Computer Interface: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Catherine Yang and Version 1 by Konstantinos Karampidis.

The field of brain–computer interface (BCI) enables us to establish a pathway between the human brain and computers, with applications in the medical and nonmedical field. Brain computer interfaces can have a significant impact on the way humans interact with machines. In recent years, the surge in computational power has enabled deep learning algorithms to act as a robust avenue for leveraging BCIs. 

  • EEG
  • deep learning
  • BCI
  • motor imagery

1. Introduction

Brain–computer interfaces (BCIs) are an emerging field of technology that combines and allows the connection between the brain and a computer or other external devices. BCIs have the potential to revolutionize the way humans interact with machines, opening countless possibilities both in medical and nonmedical domains. In the medical field, it can help people suffering from locked-in syndrome to communicate [1]. Moreover, brain–computer interfaces (BCIs) are displaying potential in the realm of neuroprosthetics, offering the prospect for individuals with limb amputations or paralysis to command robotic limbs or exoskeletons through their brain signals [2]. In epilepsy management, BCIs are researched for real-time seizure detection and intervention, potentially mitigating the impacts of seizures [3]. In the nonmedical domain, an EEG BCI has applications in areas such as gaming where players can play a game using only their thoughts [4] and in fields such as entertainment where users can control drones or other robotic devices [5].

2. Convolutional Neural Networks

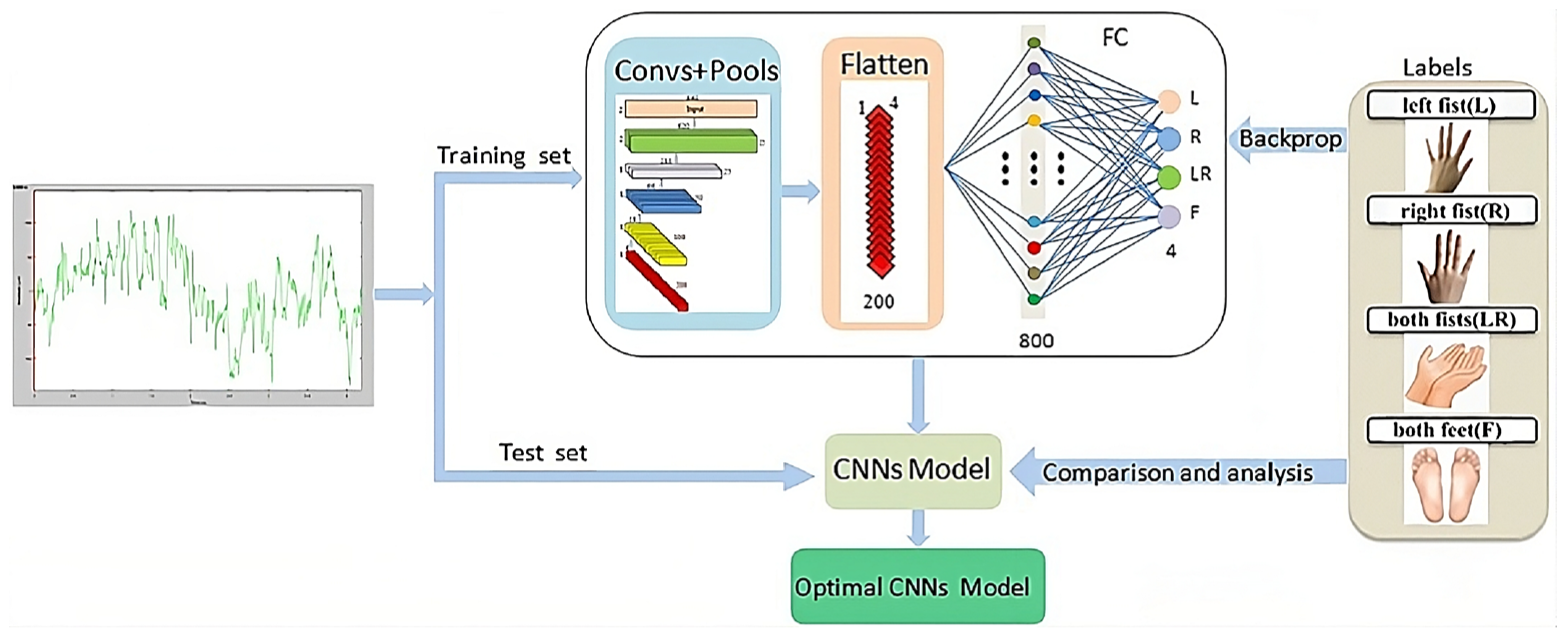
CNNs mimic the operational principles of the human visual cortex and possess the ability to dynamically comprehend spatial hierarchies in EEG data, recognizing patterns associated with motor imagery tasks through multiple layer transformations [51][6]. A CNN architecture begins with an input layer that accepts raw or preprocessed EEG data as shown in Figure 91. These data can be represented in various formats, such as time–frequency images, allowing the network to effectively process and analyze the brain signals associated with motor imagery. These data are then convolved using multiple kernels or filters, enabling the network to learn local features. Subsequently, the network employs a pooling layer for dimensionality reduction, refining the comprehension of the information. As the model progresses through these layers, it acquires the capacity to understand increasingly complex features. The final component is a fully connected (dense) classification layer that maps the learned high-level features to the desired output classes, such as different types of motor imagery, effectively acting as a decision-making layer that converts abstract representations into definitive classifications.
Figure 91. Typical EEG CNN architecture [52].
Typical EEG CNN architecture [7].
Dose et al. proposed a CNN trained on 3 s of segments from EEG signals [53][8]. The proposed method achieved an accuracy of 80.10%, 69.72%, and 59.71% on two, three, and four MI classes, respectively, on the Physionet dataset. Miao M et al. proposed a CNN with five layers to classify two motor imagery tasks, right hand and right foot, from the BCI Competition III-IV-a dataset, achieving a 90% accuracy [54][9]. Zhao et al. proposed a novel CNN with multiple spatial temporal convolution (STC) blocks and fully connected layers [55][10]. Contrastive learning was used to push the negative samples away and pull the positive samples together. This method achieved an accuracy of 74.10% on BCI III-2a, 73.62% on SMR-BCI, and 69.43% on OpenBMI datasets. Liu et al. proposed an end-to-end compact multibranch one-dimensional CNN (CMO-CNN) network for decoding MI EEG signals, achieving 83.92% and 87.19% accuracies on the BCI Competition IV-2a and the BCI Competition IV-2b datasets, respectively [56][11]. Han et al. proposed a parallel CNN (PCNN) to classify motor imagery signals [57][12]. That method, which achieved an average accuracy of 83.0% on the BCI Competition IV-2b dataset, began by projecting raw EEG signals into a low-dimensional space using a regularized common spatial pattern (RCSP) to enhance class distinctions. Then, the short-time Fourier transform (STFT) collected the mu and beta bands as frequency features, combining them to form 2D images for the PCNN input. The efficacy of the PCNN structure was evaluated against other methods such as stacked autoencoder (SAE), CNN-SAE, and CNN. Ma et al. proposed an end-to-end, shallow, and lightweight CNN framework, known as Channel-Mixing-ConvNet, aimed at improving the decoding accuracy of the EEG-Motor Raw datasets [58][13]. Unlike traditional methods, the first block of the network was designed to implicitly stack temporal–spatial convolution layers to learn temporal and spatial EEG features after EEG channels were mixed. This approach integrated the feature extraction capabilities of both layers and enhanced performance. This resulted in a 74.9% accuracy rate on the BCI IV-2a dataset and 95.0% accuracy rate on the High Gamma Dataset (HGD). Ak et al. performed an EEG data analysis to control a robotic arm. In their work, spectrogram images derived from EEG data were used as input to the GoogLeNet. They tested the system on imagined directional movements—up, down, left, and right—to control the robotic arm [59][14]. The approach resulted in the robotic arm executing the desired movements with over 90% accuracy, while on their private dataset, they achieved 92.59% accuracy. Musallam Y et al. proposed the TCNet-Fusion model, which used multiple techniques such as temporal convolutional networks (TCNs), separable convolution, depthwise convolution, and layer fusion [60][15]. This process created an imagelike representation, which was then fed into the primary TCN. During testing, the model achieved a classification accuracy of 83.73% on the four-class motor imagery of the BCI Competition IV-2a dataset and an accuracy of 94.41% on the High Gamma Dataset. Zhang et al. proposed a CNN with a 1D convolution on each channel followed by a 2D convolution to extract spatial features based on all 20 channels [61][16]. Then, to deal with the high computational cost, the idea of pruning was used, which is a technique of reducing the size and complexity of the neural network by removing certain connections or neurons. In the proposed method, a fast recursive algorithm (FRA) was applied to prune redundant parameters in the fully connected layers to reduce computational costs. The proposed architecture achieved an accuracy of 62.7% in the OPENBCI dataset. A similar approach was proposed by Vishnupriya et al. [62][17] to reduce the complexity of their architecture. The magnitude-based weight pruning was performed on the network, which achieved an accuracy of 84.46% on two MI tasks (left hand, right hand) in Lee et al.’s dataset. Shajil et al. proposed a CNN architecture to classify four MI tasks, using the common spatial pattern filter on the raw EEG signal, then using the spectrograms extracted from the filtered signals as input into the CNN [63][18]. The proposed method achieved an accuracy of 86.41% on their private dataset. Korhan et al. proposed a CNN architecture with five layers [64][19]. The proposed architecture was compared using only the CNN without any filtering, then with five different filters, and finally, with common spatial patterns followed by the CNN with the last architecture, which achieved the highest accuracy of 93.75% in the BCI Competition III-3a dataset. Alazrai et al. proposed a CNN network, with the raw signal transformed into the time–frequency domain with the quadratic time–frequency distribution (QTFD), followed by the CNN network to extract and classify the features [65][20]. The proposed method was tested on their two private datasets, with 11 MI tasks (rest, grasp-related tasks, wrist-related tasks, and finger-related tasks) and obtained accuracies of 73.7% for the able-bodied and 72.8% for the transradial-amputated subjects. Table 21 summarizes the research articles that utilize CNNs along with the tasks, the datasets used, and their performance.
Table 21.
Reviewed CNN architectures, datasets and their accuracies.
Authors Accuracy Dataset MI Tasks
Dose et al. [53][8] 59.71% EEGMMIDB LH, RH, RS, BL
[72][28] 0.8 (kappa) BCI IV-2a LH, RH, BL, T Miao M et al. [54][9] 90% BCI III-4, private RH, RF
35] proposed a deep neural network with four layers each including 50, 30, 15, and 1 node, respectively, achieving a 49.5% classification accuracy in the BCI Competition IV-2b with two MI tasks selected (arm and foot movement). Cheng et al. proposed a deep neural network which accepted as input multiple sub-bands of the raw signal extracted by a sliding window strategy [80][36]. Under these sub-bands, diverse spatial–spectral features were extracted and fed into a deep neural network for classification, achieving an accuracy of 71.5% on their private dataset. Yohanandan et al. proposed a binary classifier (relaxed and right-handed MI tasks) using a deep neural network with the μ-rhythm (8–12 Hz frequency) data being fed into the network [81][37]. The authors used different sliding windows from 1 s to 9 s to determine the highest-accuracy window. An average accuracy of ~83% was achieved on their privately collected dataset from seven human volunteers. Kumar et al. proposed a deep neural network for the classification of extracted features using a common spatial pattern in the BCI Competition III-4a dataset, achieving an accuracy of ~85% on two MI tasks (right hand and left foot) [82][38]. Table 43 shows the performance of each one of the aforementioned architectures.
Table 43.
Reviewed deep neural network architectures and their accuracies.
Authors Accuracy Dataset MI Tasks
Suhaimi et al. [79][35] 49.5% BCI Competition 2b LH, RH
Wei et al. [70][25] 81.8%, 54.8% BCI IV-2a, private LH, RH
Zhao R et al. [
Cheng et al. [80][36] 71.5% Private LH, RH 55][10] 74.10%, 73.62%, 69.43% BCI III-2a, SMR-BCI, OpenBMI RH, RF
Liu X et al. [56][11] 83.92%, 87.19% BCI IV-2a, BCI IV-2b LH, RH, BL, T
[40].
Autthasan et al. proposed an end-to-end multitask autoencoder and tested it on three datasets, BCI Competition IV-2a, SMR-BCI, and OpenBMI, achieving accuracies of 70.09%, 72.95%, and 66.51%, respectively [85][41]. Similarly, capsule networks, which introduce a hierarchical structure to capture pose and viewpoint information, have shown promising results in MI task classification [86][42]. Capsules in capsule networks utilize vector-based representations. This property enables the network to capture hierarchical relationships and spatial dependencies among features. Each capsule comprises a group of neurons, with each neuron’s output representing a different property of the same feature, enabling the recognition of the whole entity by first identifying its parts. Ha et al. proposed a capsule network, using the images extracted with the short-time Fourier transform as input to the capsule network [87][43]. Their proposed method achieved a 77% accuracy on the BCI competition IV-2b dataset (left-hand and right-hand MI tasks). Long short-term memory (LSTM) networks [88][44], a type of recurrent neural network, have been utilized to model temporal dependencies in MI data, enabling effective sequence learning for classification. Leon-Urbano et al. proposed an LSTM approach on an MNE python library dataset which consisted of two MI tasks (feet, hands), and after fine-tuning their model, they achieved a 90% accuracy [89][45]. Saputra et al. also deployed an LSTM network on the BCI Competition IV-2a dataset, achieving an accuracy of 49.65% [90][46]. Hwang et al. also performed a classification based on an LSTM on the BCI competition IV-2a dataset with a feature extraction based on overlapping band-based FBCSP (filter-bank common spatial pattern), with an accuracy of 97% [91][47]. Ma et al. proposed a parallel architecture including a temporal LSTM and a spatial bidirectional LSTM [92][48]. The proposed method was tested on the four MI tasks (moving both feet, both fists, left fist and right fist) from the EEGMMIDB dataset and achieved an accuracy of 68.20%. Another proposed method is the restricted Boltzmann machine [93][49], a type of probabilistic graphical model, leveraging its ability to model joint probability distributions. Xu et al. utilized a restricted Boltzmann machine and a support vector machine (SVM) to classify and recognize deep multiview features [94][50]. The proposed method achieved an accuracy of 78.50% on the BCI competition IV-2a dataset. Moreover, metalearning [95][51] empowers models to acquire the skill of learning on their own, with a limited quantity of data. This is achieved through training the model on a diverse range of tasks, allowing it to leverage the knowledge gained from these tasks when presented with new challenges. Among the various metalearning algorithms, one of the most prominent ones is MAML (model-agnostic metalearning) [95][51]. MAML trains the model to efficiently update its parameters, facilitating a rapid adaptation to new tasks with minimal updates. Li et al. proposed a metalearning method which learned from the output of other machine learning algorithms [96][52]. The proposed method achieved an 80% accuracy on the Physionet dataset (on left fist vs. right fist and both fists vs. both feet). Contrastive learning [97][53] is a self-supervised learning technique that aims to create meaningful representations by contrasting positive and negative pairs of data. Han et al. proposed the so-called contrastive learning network. The proposed method was tested on the BCI competition IV-2a dataset achieving an accuracy of 79.54% when all the training labels were used [98][54]. A deep belief network (DBN) [99][55] is an unsupervised neural network known for its feature extraction from raw data. It uses a two-step training process: unsupervised pretraining with a restricted Boltzmann machine and supervised fine-tuning. Li et al. proposed a deep belief architecture where the time–frequency information from the raw EEG signal was fed into the DBN, which was used for the identification and classification [100][56]. The proposed method achieved an accuracy of 93.57% on the BCI competition II-3 dataset. A synopsis of the above-mentioned proposals can be found in Table 54.
Table 54.
Other reviewed deep learning architectures and their accuracies.
Authors Accuracy Dataset MI Tasks Architecture
Autthasan et al. [85][41] 70.09%, 72.95%

66.51%		 BCI IV-2a, SMR_BCI, Open BCI LH, RH, BL, T Autoencoder
Ha et al. [87][43] 77% BCI IV-2b
Limpiti et al. [73][29] 95.03%, 91.86% BCI IV-2a LH, RH, BL, T
LH, RH Capsule network Yohonanndan et al. [81][37] 83% Private RS, RH
Urbano et al. [89][45] 90% MNE dataset Han et al. [57][12] 83% BCI IV-2b LH, RH
Ma et al. [58][13] 74.9%, 95.0% BCI IV-2a, HGD LH, RH, BL, T
Ak et al. [59][14] 92.59% Private U, D, L, R
Musallam et al. [60][15] 83.73%, 94.41% BCI IV-2a, HGD LH, RH, BL, T
Zhang et al. [61][16] 62.7% OpenBMI LH, RH
Vishnupriya et al. [62][17] 84.46% Lee et al. LH, RH
Shajil et al. [63][18] 86.41% Private LH, RH, BH, BL
Korhan et al. [64][19] 93.75% BCI III-3a LH, RH, BL, T
Alazrai et al. [65][20] 73.7%, 72.8% Private RS, SDG, LG, ETG, RDW, EW, FI, FM, FR, FL, FT
LH: left hand, RH: right hand, RL: right leg, BL: both legs, T: tongue, RS: resting state, BF: Both fists, LF: left fist, RF: right fist, U: up, D: down, L: left, R: right, SDG: small-diameter grasp, LG: lateral grasp, ETG: extension-type grasp, RDW: ulnar and radial deviation of the wrist, EW: extension of the wrist, FI: flexion and extension of the index finger, FM: flexion and extension of the middle finger, FR: flexion and extension of the ring finger, FL: flexion and extension of the little finger.

3. Transfer Learning

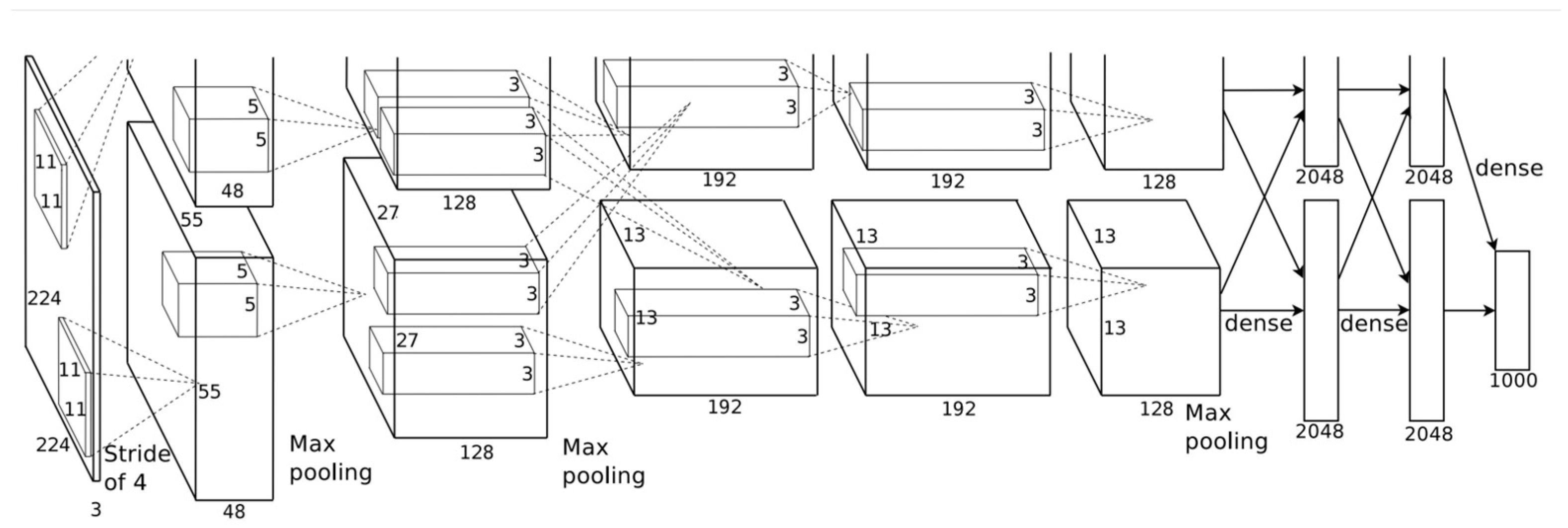
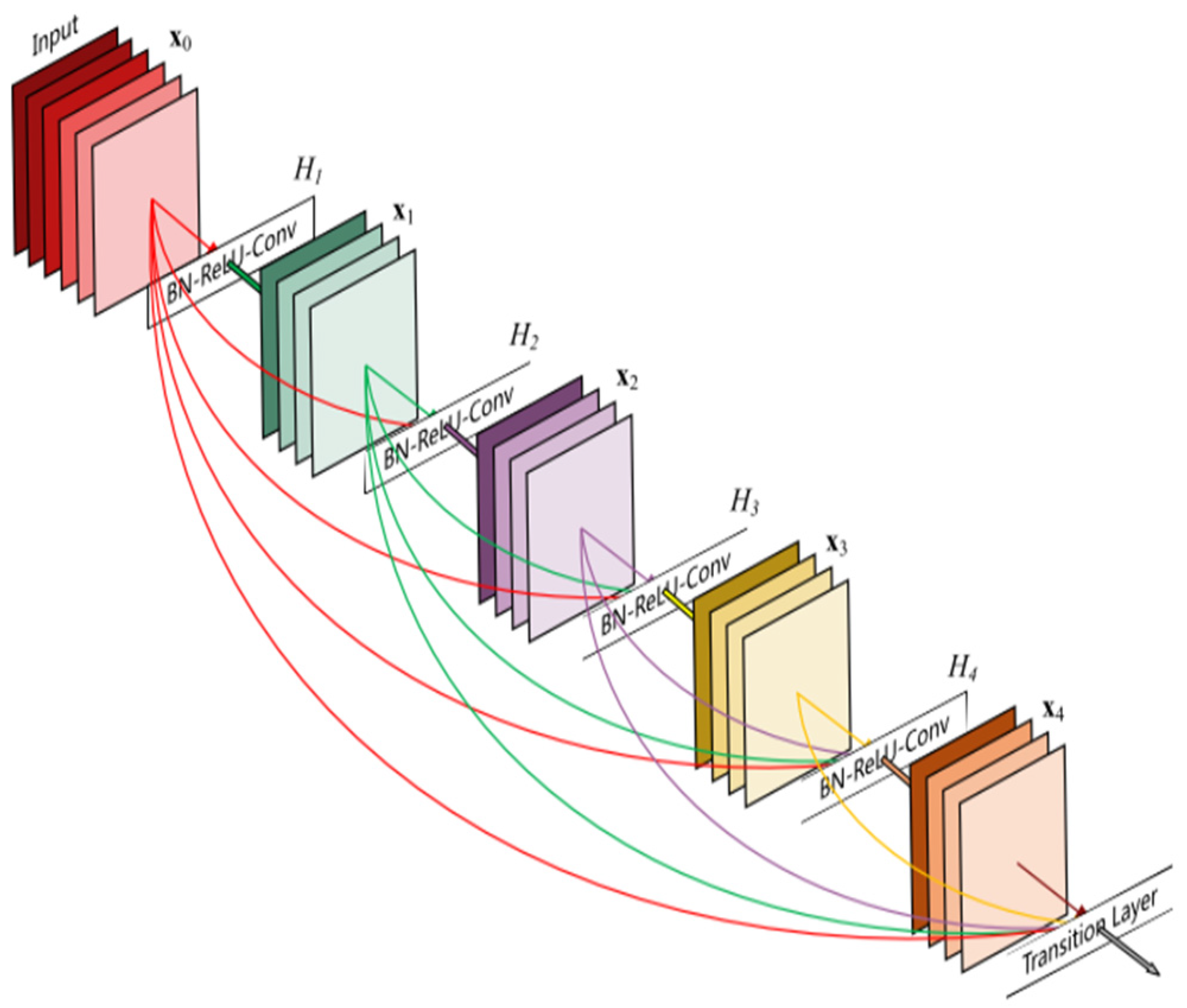
In the realm of machine learning, transfer learning offers a valuable approach to improve model performance and efficiency. It involves leveraging the knowledge learned from one task and applying it to a different but related task. The foundation of transfer learning lies in pretrained models, which have been trained on large-scale datasets. This approach is beneficial when considering the computational resources required for training deep learning models from scratch, i.e., time, complexity, and hardware. Transfer learning also offers a noble solution when available training data are not enough to train effectively novel deep learning models. In these situations, where collecting training data is hard or expensive, as in the case of EEG data, a need to develop robust models using available data from diverse domains arises. However, the effectiveness of transfer learning relies on the learned features from the initial task being general and applicable to the target task. Some popular deep learning models utilized for transfer learning are AlexNet [66][21], ResNet18 [67][22], ResNet50, InceptionV3 [68][23], and ShuffleNet [69][24]. These models are CNN networks trained on millions of images to classify different classes. For example, AlexNet consists of eight layers with weights, the first five are convolutional layers followed by max-pooling layers, and the last three layers are fully connected layers followed by a softmax layer to provide a probability distribution over the 1000 class labels. Figure 102 shows the architecture of the AlexNet architecture.
Figure 102. AlexNet architecture [66].
AlexNet architecture [21].
ResNet (residual network) is a deep learning model in which the weight layers learn residual functions with reference to the layer inputs. This method addresses the problem of vanishing gradients in deep neural networks by introducing skip connections, also known as residual blocks. The information can flow directly across multiple layers, making it easier for the network to learn complex features. There are various versions of ResNet utilized for EEG classification, e.g., ResNet34, ResNet50, etc. Figure 113 shows the architecture of ResNet.
Figure 113. Architecture of the ResNet [67].
Architecture of the ResNet [22].
While some research papers rely on pretrained models for transfer learning, others take a different approach. Let N be the total number of subjects in a dataset. Researchers train a custom CNN on N–1 subjects, and afterwards, they use the trained CNN as a base model for transfer learning. That is, they use the remaining N subject to train the aforementioned CNN, and afterwards, they finetune the whole model. Moreover, some research papers ([70,71][25][26]) opt for alternative architectures, such as the one proposed by Schirrmeister et al. [43][27], to facilitate transfer learning in their studies. Zhang et al. utilized transfer learning to train a hybrid deep neural network (HDNN-TL) which consisted of a convolutional neural network and a long short-term memory model, to decode the spatial and temporal features of the MI signal simultaneously [72][28]. The classification performance on the BCI Competition IV-2a dataset by the proposed HDNN-TL in terms of kappa value was 0.8 (outperforming the rest of the examined methods). Wei et al. [70][25] proposed a multibranch deep transfer network, the Separate-Common-Separate Network (SCSN) based on splitting the network’s feature extractors for individual subjects, and they also explored the possibility of applying maximum mean discrepancy (MMD) to the SCSN (SCSN-MMD). They tested their models on the BCI Competition IV-2a dataset and their own online recorded dataset, which consisted of five subjects (male) and four motor imageries (relaxing, left hand, right hand, and both feet). The results showed that the proposed SCSN achieved an accuracy of (81.8%, 53.2%) and SCSN-MMD achieved an accuracy of (81.8%, 54.8%). Limpiti et al. used a continuous wavelet transform (CWT) to construct the scalograms from the raw signal, which served as input to five pretrained networks (AlexNet, ResNet18, ResNet50, InceptionV3, and ShuffleNet) [73][29]. The models were evaluated on the BCI Competition IV-2a dataset. On binary (left hand vs. right hand) and four-class (left hand, right hand, both feet, and tongue) classification, the ResNet18 network achieved the best accuracies at 95.03% and 91.86%. Wei et al. [74][30] utilized a CWT to convert the one-dimensional EEG signal into a two-dimensional time–frequency amplitude representation as the input of a pre-trained AlexNet and fine-tuned it to classify two types of MI signals (left hand and right hand). The proposed method achieved a 93.43% accuracy on the BCI Competition II-3 dataset. Arunabha proposed a multiscale feature-fused CNN (MSFFCNN) efficient transfer learning (TL) and four different variations of the model including subject-specific, subject-independent, and subject-adaptive classification models to exploit the full learning capacity of the classifier [75][31]. The proposed method achieved a 94.06% accuracy on for four different MI classes (i.e., left hand, right hand, feet, and tongue) on the BCI Competition IV-2a dataset. Chen et al. proposed a subject-weighted adaptive transfer learning method in conjunction with MLP and CNN classifiers, achieving an accuracy of 96% on their own recorded private dataset [76][32]. Zhang et al. proposed five schemes for the adaptation of a CNN to two-class motor imagery (left hand, right hand), and after fine-tuning their architecture, they achieved an accuracy of 84.19% on the public GigaDB dataset [71][26]. Solorzano et al. proposed a method based on transfer learning in neural networks to classify the signals of multiple persons at a time [77][33]. The resulting neural network classifier achieved a classification accuracy of 73% on the evaluation sessions of four subjects at a time and 74% on three at a time on the BCI Competition IV-2a dataset. Li et al. proposed a cross-channel specific–mutual feature transfer learning (CCSM-FT) network model with training tricks used to maximize the distinction between the two kinds of features [78][34]. The proposed method achieved an 80.26% accuracy on the BCI Competition IV-2a dataset. A summary of the aforementioned methods can be found in Table 32.
Table 32.
Reviewed transfer learning architectures and their accuracies.
Authors Accuracy Dataset MI Tasks
Zang et al.
BF, BH
LSTM
Wei M et al. [74][30] 93.43% BCI II-3 LH, RH
Kumar et al. [82][38] ~85% BCI Competition III-4a RH, LF
Saputra et al. [90][46] 49.65% BCI IV-2a LH, RH, BL, T LSTM Arunabha M. [75][31] 94.06% BCI IV-2a LH, RH, BL, T
Hwang et al. [91][47] 97% BCI IV-2a LH, RH, BL, T LSTM Chen et al. [76][32]
Ma et al. [92][48]96% Private F, B, L, R, S
Zhang et al. [71][26] 84.19% GigaDB LH, RH
Solorzano et al. [77][33] 74% BCI IV-2a LH, RH, BL, T
Li D et al. [78][34] 80.26% BCI IV-2a LH, RH, BL, T
LH: left hand, RH: right hand, RL: right leg, BL: both legs, T: tongue, RS: resting state, BF: Both fists, LF: left fist, RF: right fist, F: forward, B: backward, L: left, R: right, R: rest, S: stop.

4. Deep Neural Networks

Deep neural networks, a subset of artificial neural networks, have the ability to tackle complex problems. Unlike shallow neural networks that consist of only a few layers, deep neural networks are characterized by their depth, featuring multiple hidden layers between the input and output layers. Each hidden layer progressively extracts higher-level features from the data, allowing the network to learn complex representations and patterns from vast quantities of data. Suhaimi et al. [79][
LH: left hand, RH: right hand, LF: left foot, RS: resting state.

5. Others

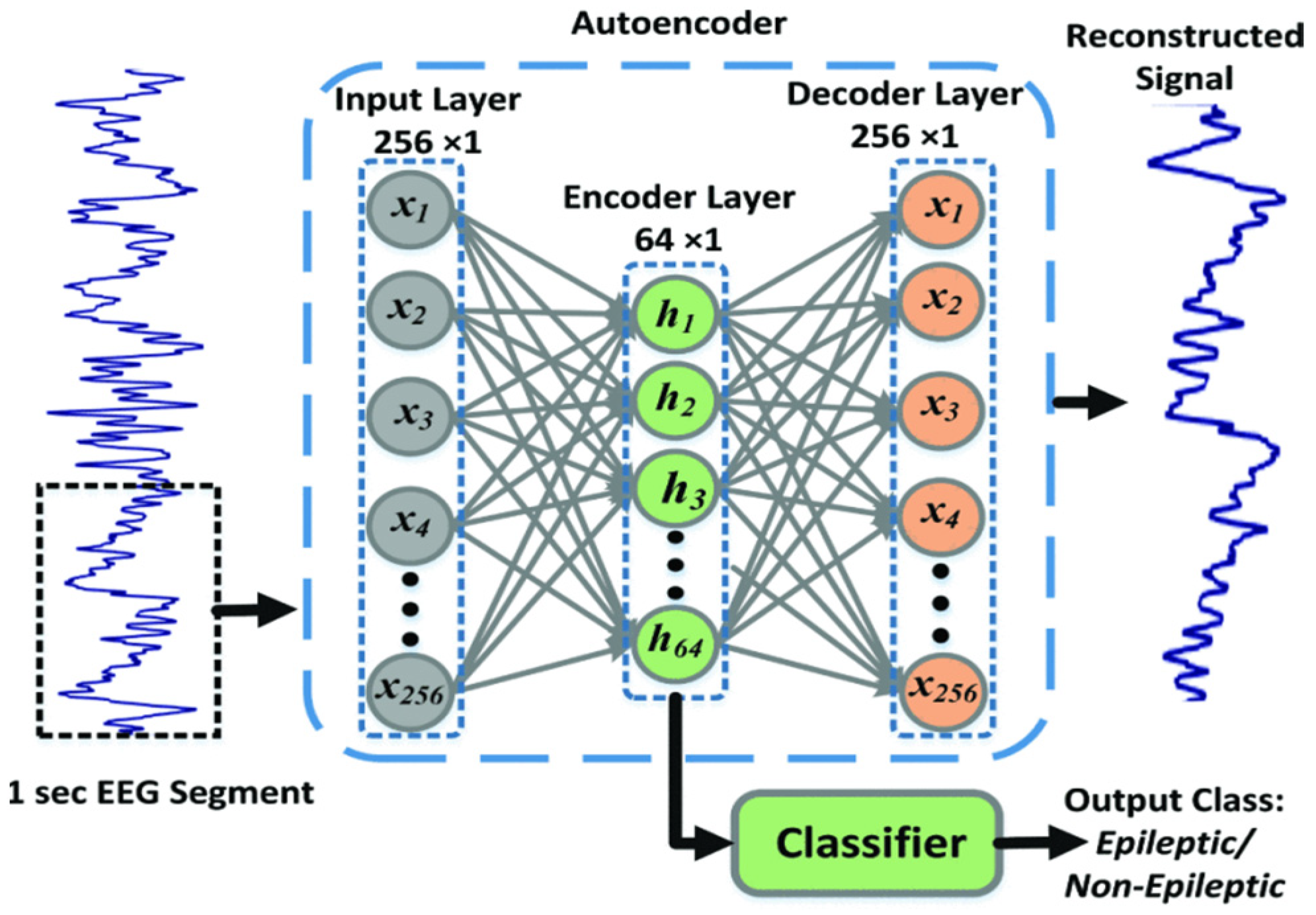
Several alternative methods have been proposed for classifying motor imagery (MI) tasks, aiming at leveraging the potential of different deep learning techniques. Autoencoders [83][39], which are designed for data reconstruction, have been explored in the context of MI task classification. Autoencoders are neural network architectures that consist of two main phases: encoding and decoding. During the encoding phase, the input signal is passed through a neural network with a progressively reduced number of neurons in each layer until it reaches the bottleneck layer, which has a lower dimensionality compared to the input data. In the decoding phase, the network strives to reconstruct the original signal from this lower-dimensional representation, preserving essential information. This encoding stage in autoencoders enables them to effectively learn compressed representations of input data, such as EEG data, by reducing its dimensionality while retaining significant information. Figure 124 shows an autoencoder used to reconstruct an EEG signal.
Figure 124. Autoencoder architecture [84].
Autoencoder architecture
68.20%
EEGMMIDB
LF, RF, BL, BF
LSTM, bi-LSTM
Xu et al. [94][50] 78.50% BCI IV-2a LH, RH, BL, T Boltzmann Machine
Li et al. [96][52] 80% EEGMMIDB LF, RF, BL, BF Meta-learning
Han et al. [98][54] 79.54% BCI IV-2a LH, RH, BL, T Contrastive learning
Li et al. [100][56] 93.57% BCI II-3 LH, RH Deep belief network
LH: left hand, RH: right hand, RL: right leg, BL: both legs, T: tongue, RS: resting state, BF: both fists, LF: left fist, RF: right fist.

References

  1. Wolpaw, J.R.; Birbaumer, N.; McFarland, D.J.; Pfurtscheller; Vaughan, T.M. Brain–computer interfaces for communication and control. Clin. Neurophysiol. 2002, 113, 767–791.
  2. Tariq, M.; Trivailo, P.M.; Simic, M. EEG-Based BCI Control Schemes for Lower-Limb Assistive-Robots. Front. Hum. Neurosci. 2018, 12, 312.
  3. Maksimenko, V.A.; van Heukelum, S.; Makarov, V.V.; Kelderhuis, J.; Lüttjohann, A.; Koronovskii, A.A.; Hramov, A.E.; van Luijtelaar, G. Absence Seizure Control by a Brain Computer Interface. Sci. Rep. 2017, 7, 2487.
  4. Bonnet, L.; Lotte, F.; Lecuyer, A. Two brains, one game: Design and evaluation of a multiuser bci video game based on motor imagery. IEEE Trans. Comput. Intell. AI Games 2013, 5, 185–198.
  5. Belkacem, A.N.; Lakas, A. A Cooperative EEG-based BCI Control System for Robot-Drone Interaction. In Proceedings of the 2021 International Wireless Communications and Mobile Computing, IWCMC, Harbin, China, 28 June–2 July 2021; pp. 297–302.
  6. Saxena, A. An Introduction to Convolutional Neural Networks. Int. J. Res. Appl. Sci. Eng. Technol. 2015, 10, 943–947.
  7. Lun, X.; Yu, Z.; Chen, T.; Wang, F.; Hou, Y. A Simplified CNN Classification Method for MI-EEG via the Electrode Pairs Signals. Front. Hum. Neurosci. 2020, 14, 559321.
  8. Dose, H.; Møller, J.S.; Puthusserypady, S.; Iversen, H.K. A deep learning MI-EEG classification model for BCIS. In Proceedings of the European Signal Processing Conference, Rome, Italy, 3–7 September 2018; Volume 2018, pp. 1676–1679.
  9. Miao, M.; Hu, W.; Yin, H.; Zhang, K. Spatial-Frequency Feature Learning and Classification of Motor Imagery EEG Based on Deep Convolution Neural Network. Comput. Math. Methods Med. 2020, 2020, 1981728.
  10. Zhao, R.; Wang, Y.; Cheng, X.; Zhu, W.; Meng, X.; Niu, H.; Cheng, J.; Liu, T. A mutli-scale spatial-temporal convolutional neural network with contrastive learning for motor imagery EEG classification. Med. Nov. Technol. Devices 2023, 17, 100215.
  11. Liu, X.; Xiong, S.; Wang, X.; Liang, T.; Wang, H.; Liu, X. A compact multi-branch 1D convolutional neural network for EEG-based motor imagery classification. Biomed. Signal Process Control 2023, 81, 104456.
  12. Han, Y.; Wang, B.; Luo, J.; Li, L.; Li, X. A classification method for EEG motor imagery signals based on parallel convolutional neural network. Biomed. Signal Process Control 2022, 71, 103190.
  13. Ma, W.; Gong, Y.; Zhou, G.; Liu, Y.; Zhang, L.; He, B. A channel-mixing convolutional neural network for motor imagery EEG decoding and feature visualization. Biomed. Signal Process Control 2021, 70, 103021.
  14. Ak, A.; Topuz, V.; Midi, I. Motor imagery EEG signal classification using image processing technique over GoogLeNet deep learning algorithm for controlling the robot manipulator. Biomed. Signal Process Control 2022, 72, 103295.
  15. Musallam, Y.K.; AlFassam, N.I.; Muhammad, G.; Amin, S.U.; Alsulaiman, M.; Abdul, W.; Altaheri, H.; Bencherif, M.A.; Algabri, M. Electroencephalography-based motor imagery classification using temporal convolutional network fusion. Biomed. Signal Process Control 2021, 69, 102826.
  16. Zhang, J.; Li, K. A Pruned Deep Learning Approach for Classification of Motor Imagery Electroencephalography Signals. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Glasgow, Scotland, UK, 11–15 July 2022; Volume 2022, pp. 4072–4075.
  17. Vishnupriya, R.; Robinson, N.; Reddy, R.; Guan, C. Performance Evaluation of Compressed Deep CNN for Motor Imagery Classification using EEG. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Mexico, Russia, 1–5 November 2021; pp. 795–799.
  18. Shajil, N.; Mohan, S.; Srinivasan, P.; Arivudaiyanambi, J.; Murrugesan, A.A. Multiclass Classification of Spatially Filtered Motor Imagery EEG Signals Using Convolutional Neural Network for BCI Based Applications. J. Med. Biol. Eng. 2020, 40, 663–672.
  19. Korhan, N.; Dokur, Z.; Olmez, T. Motor imagery based EEG classification by using common spatial patterns and convolutional neural networks. In Proceedings of the 2019 Scientific Meeting on Electrical-Electronics and Biomedical Engineering and Computer Science, EBBT 2019, Istanbul, Turkey, 24–26 April 2019.
  20. Alazrai, R.; Abuhijleh, M.; Alwanni, H.; Daoud, M.I. A Deep Learning Framework for Decoding Motor Imagery Tasks of the Same Hand Using EEG Signals. IEEE Access 2019, 7, 109612–109627.
  21. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process Syst. 2012, 25, 84–90.
  22. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; Volume 2016, pp. 770–778.
  23. Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A.; Liu, W.; et al. Going Deeper with Convolutions. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9.
  24. Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856.
  25. Wei, X.; Ortega, P.; Faisal, A.A. Inter-subject deep transfer learning for motor imagery EEG decoding. In Proceedings of the International IEEE/EMBS Conference on Neural Engineering, NER, Virtual Event, 4–6 May 2021; pp. 21–24.
  26. Zhang, K.; Robinson, N.; Lee, S.W.; Guan, C. Adaptive transfer learning for EEG motor imagery classification with deep Convolutional Neural Network. Neural Netw. 2021, 136, 1–10.
  27. Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420.
  28. Zhang, R.; Zong, Q.; Dou, L.; Zhao, X.; Tang, Y.; Li, Z. Hybrid deep neural network using transfer learning for EEG motor imagery decoding. Biomed. Signal Process Control 2021, 63, 102144.
  29. Limpiti, T.; Seetanathum, K.; Sricom, N.; Puttarak, N. Transfer Learning for Classifying Motor Imagery EEG: A Comparative Study. In Proceedings of the BMEiCON 2021-13th Biomedical Engineering International Conference, Ayutthaya, Thailand, 19–21 November 2021.
  30. Wei, M.; Yang, R.; Huang, M. Motor imagery EEG signal classification based on deep transfer learning. Proc. IEEE Symp. Comput. Based Med. Syst. 2021, 2021, 85–90.
  31. Roy, A.M. Adaptive transfer learning-based multiscale feature fused deep convolutional neural network for EEG MI multiclassification in brain–computer interface. Eng. Appl. Artif. Intell. 2022, 116, 105347.
  32. Chen, C.Y.; Wang, W.J.; Chen, C.C. Multiclass Classification of EEG Motor Imagery Signals Based on Transfer Learning. In Proceedings of the 2022 8th International Conference on Applied System Innovation, ICASI, Nantou, Taiwan, 22–23 April 2022; pp. 140–143.
  33. Solorzano-Espindola, C.E.; Zamora, E.; Sossa, H. Multi-subject classification of Motor Imagery EEG signals using transfer learning in neural networks. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Mexico, Russia, 1–5 November 2021; pp. 1006–1009.
  34. Li, D.; Wang, J.; Xu, J.; Fang, X.; Ji, Y. Cross-Channel Specific-Mutual Feature Transfer Learning for Motor Imagery EEG Signals Decoding. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: New York, NY, USA, 2023.
  35. Suhaimi, N.S.; Yusoff, M.Z.; Saad, M.N.M. Artificial Neural Network Analysis on Motor Imagery Electroencephalogram. In Proceedings of the 2022 IEEE 5th International Symposium in Robotics and Manufacturing Automation (ROMA), Malacca, Malaysia, 6–8 August 2022; IEEE: New York, NY, USA, 2022.
  36. Cheng, D.; Liu, Y.; Zhang, L. Exploring Motor Imagery EEG Patterns for Stroke Patients with Deep Neural Networks. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing-Proceedings, Calgary, AB, Canada, 15–20 April 2018; pp. 2561–2565.
  37. Yohanandan, S.A.C.; Kiral-Kornek, I.; Tang, J.; Mshford, B.S.; Asif, U.; Harrer, S. A Robust Low-Cost EEG Motor Imagery-Based Brain-Computer Interface. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Honolulu, HI, USA, 18–21 July 2018; pp. 5089–5092.
  38. Kumar, S.; Sharma, A.; Mamun, K.; Tsunoda, T. A Deep Learning Approach for Motor Imagery EEG Signal Classification. In Proceedings of the Proceedings-Asia-Pacific World Congress on Computer Science and Engineering 2016 and Asia-Pacific World Congress on Engineering 2016, APWC on CSE/APWCE 2016, Nadi, Fiji, 5–6 December 2016; pp. 34–39.
  39. Pinaya, W.H.L.; Vieira, S.; Garcia-Dias, R.; Mechelli, A. Autoencoders. In Machine Learning: Methods and Applications to Brain Disorders; Academic Press: Cambridge, MA, USA, 2020; pp. 193–208.
  40. Khan, G.H.; Khan, N.A.; Altaf, M.A.B.; Abid, M.U.R. Classifying Single Channel Epileptic EEG data based on Sparse Representation using Shallow Autoencoder. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Mexico, Russia, 1–5 November 2021; pp. 643–646.
  41. Autthasan, P.; Chaisaen, R.; Sudhawiyangkul, T.; Rangpong, P.; Kiatthaveephong, S.; Dilokthanakul, N.; Bhakdisongkhram, G.; Phan, H.; Guan, C.; Wilaiprasitporn, T. MIN2Net: End-to-End Multi-Task Learning for Subject-Independent Motor Imagery EEG Classification. IEEE Trans. Biomed. Eng. 2022, 69, 2105–2118.
  42. Patrick, M.K.; Adekoya, A.F.; Mighty, A.A.; BEdward, Y. Capsule Networks—A survey. J. King Saud. Univ.-Comput. Inf. Sci. 2022, 34, 1295–1310.
  43. Ha, K.W.; Jeong, J.W. Decoding Two-Class Motor Imagery EEG with Capsule Networks. In Proceedings of the 2019 IEEE International Conference on Big Data and Smart Computing, BigComp 2019-Proceedings, Kyoto, Japan, 27 February–2 March 2019.
  44. Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780.
  45. Leon-Urbano, C.; Ugarte, W. End-to-end electroencephalogram (EEG) motor imagery classification with Long Short-Term. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence, SSCI, Canberra, ACT, Australia, 1–4 December 2020; pp. 2814–2820.
  46. Saputra, M.F.; Setiawan, N.A.; Ardiyanto, I. Deep Learning Methods for EEG Signals Classification of Motor Imagery in BCI. IJITEE (Int. J. Inf. Technol. Electr. Eng.) 2019, 3, 80–84.
  47. Hwang, J.; Park, S.; Chi, J. Improving Multi-Class Motor Imagery EEG Classification Using Overlapping Sliding Window and Deep Learning Model. Electronics 2023, 12, 1186.
  48. Ma, X.; Qiu, S.; Du, C.; Xing, J.; He, H. Improving EEG-Based Motor Imagery Classification via Spatial and Temporal Recurrent Neural Networks. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Honolulu, HI, USA, 18–21 July 2018; pp. 1903–1906.
  49. Yan, W.Q. Boltzmann Machines. In Computational Methods for Deep Learning; Texts in Computer Science; Springer: Cham, Switzerland, 2021.
  50. Xu, J.; Zheng, H.; Wang, J.; Li, D.; Fang, X. Recognition of EEG Signal Motor Imagery Intention Based on Deep Multi-View Feature Learning. Sensors 2020, 20, 3496.
  51. Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the 34th International Conference on Machine Learning, ICML, Sydney, Australia, 6–11 August 2017; Volume 3, pp. 1856–1868. Available online: https://arxiv.org/abs/1703.03400v3 (accessed on 24 July 2023).
  52. Li, D.; Ortega, P.; Wei, X.; Faisal, A. Model-agnostic meta-learning for EEG motor imagery decoding in brain-computer-interfacing. In Proceedings of the International IEEE/EMBS Conference on Neural Engineering, NER, Vitual, 4–6 May 2021; pp. 527–530.
  53. Le-Khac, P.H.; Healy, G.; Smeaton, A.F. Contrastive Representation Learning: A Framework and Review. IEEE Access 2020, 8, 193907–193934.
  54. Han, J.; Gu, X.; Lo, B. Semi-Supervised Contrastive Learning for Generalizable Motor Imagery EEG Classification. In Proceedings of the 2021 IEEE 17th International Conference on Wearable and Implantable Body Sensor Networks, BSN, Athens, Greece, 27–30 July 2021.
  55. Hua, Y.; Guo, J.; Zhao, H. Deep Belief Networks and deep learning. In Proceedings of the 2015 International Conference on Intelligent Computing and Internet of Things, ICIT, Harbin, China, 17–18 January 2015; pp. 1–4.
  56. Li, M.-A.; Zhang, M.; Sun, Y.-J. A novel motor imagery EEG recognition method based on deep learning. In 2016 International Forum on Management, Education and Information Technology Application; Atlantis Press: Amsterdam, The Netherlands, 2016; pp. 728–733.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback