Explainable Artificial Intelligence in Medicine: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Lindsay Dong and Version 1 by Esteban García-Cuesta.

Due to the success of artificial intelligence (AI) applications in the medical field over the past decade, concerns about the explainability of these systems have increased. The reliability requirements of black-box algorithms for making decisions affecting patients pose a challenge even beyond their accuracy. Recent advances in AI increasingly emphasize the necessity of integrating explainability into these systems. While most traditional AI methods and expert systems are inherently interpretable, the recent literature has focused primarily on explainability techniques for more complex models such as deep learning.

  • artificial intelligence
  • medicine
  • explainable AI
  • interpretable AI

1. Classification of Explainability Approaches

Several taxonomies have been proposed in the literature to classify Explainable XAIArtificial Intelligence (XAI) methods and approaches, depending on different criteria [40,41,42][1][2][3] (Figure 31).
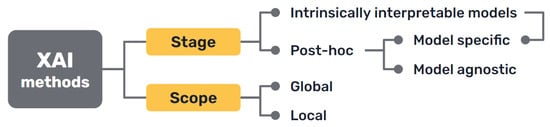
Applsci 13 10778 g003
Figure 31.
Most common approaches to the classification of XAI methods.
First, there is a clear distinction between auxiliary techniques that aim to provide explanations for either the model’s prediction or its inner workings, which are commonly called post hoc explainability methods, and AI models that are intrinsically interpretable, either because of their simplicity, the features they use or because they have a straightforward structure that is readily understandable by humans.
Secondly, it can distinguish interpretability techniques by their scope, where explanations provided by an XAI approach can be local, meaning that they refer to particular predictions of the model, or global, if they try to describe the behaviour of the model as a whole.
Other differentiations can be made between interpretability techniques that are model specific, because they have requirements regarding the kind of data or algorithm used, and model agnostic methods, that are general and can be applied in any case. Intrinsically interpretable models are model specific by definition, but post hoc explainability methods can be generally seen as model agnostic, though some of them can have some requisites regarding the data or structure of the model.
More classifications can be made regarding how characteristics of the output explanations are displayed (textual, visual, rules, etc.), the type of input data required, the type of problem they can be applied to [42][3] or how they are produced [30][4].

2. Intrinsically Interpretable Models

Intrinsically interpretable models are those built using logical relations, statistical or probabilistic frameworks, and similar strategies that represent human-interpretable systems, since they use rules, relationships or probabilities assigned to known variables. This approach to explainable AI, despite receiving less attention in recent years while the focus has been on DL, is historically the original one, and the perspective taken by knowledge-based systems.

2.1. Classical Medical Knowledge-Based Systems

Some knowledge-based systems, commonly known as “expert systems”, are some of the classical AI models that were first developed at the end of the 1960s. Explanations were sometimes introduced as a feature of these first rule-based expert systems by design, as they were needed not only by users, but also by developers, to troubleshoot their code during the design of these models. Thus, the importance of AI explainability has been discussed since the 1970s [44,45][5][6]. In medicine, many of these systems were developed aiming to be an aid for clinicians during the diagnosis of patients and treatment assignment [46][7]. It must reiterate that explanations for patient cases are not easily made, in many cases, by human medical professionals. The most widely known of these classical models was MYCIN [47][8], but many more based on causal, taxonomic, and other networks of semantic relations, such as CASNET, INTERNIST, the Present Illiness Program, and others, were designed to support rules by models of underlying knowledge that explained the rules and drove the inferences in clinical decision-making [37,48,49][9][10][11]. Subsequently, the modelling of explanations was pursued explicitly for the MYCIN type of rule-based models [50][12]. The role of the explanation was frequently recognised as a major aspect of expert systems [51,52,53][13][14][15]. As shown in Figure 42, expert systems consist of a knowledge base containing the expertise captured from human experts in the field, usually in the form of rules, including both declarative or terminological knowledge and procedural knowledge of the domain [45][6]. This knowledge base is consulted by an inference algorithm when the user interacts with the system, and an explanation facility interacts with both the inference system and the knowledge base to construct the corresponding explaining statements [54][16].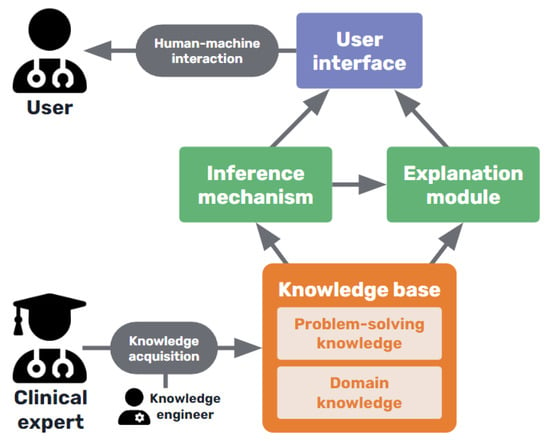
Applsci 13 10778 g004
Figure 42.
Basic diagram of a medical knowledge-based expert system.
The explanations provided were pre-modeled [55][17] and usually consisted of tracing the rules used by the inference mechanism to arrive at the final decision and present them in an intelligible way to the user. Such an approach aimed to explain how and why the system produced a diagnosis [53][15] and, in some more sophisticated cases, even the causal evolution of the patient’s clinical status [56][18]. However, these explanations were limited by the knowledge base constructed by the system’s designers; all the justifications for knowledge had to be explicitly captured to produce specific explanations [53][15]. Knowledge acquisition (KA) and updating is a challenging task  and this was not efficiently resolved, leading KA to become the bottleneck that resulted in the decline of interest in knowledge-based AI systems (as a main example of symbolic AI) in favour of data-based AI and ML systems.

2.2. Interpretable Machine Learning Models

As an alternative to knowledge-based systems, from the early days of medical decision making, statistical Bayesian, Hypothesis-Testing, and linear discriminant models were ML models that can be considered interpretable. They are based on the statistical relationships extracted from clinical databases which allow formal probabilistic inferential methods to be applied. Ledley and Lusted proposed the Bayesian approach in their pioneering article in the journal 𝑆𝑐𝑖𝑒𝑛𝑐𝑒 in 1959 [57][19], with many of the alternatives first discussed in The Diagnostic Process conference [58][20]. Logistic regression is an effective statistical approach that can be used for classification and prediction. Generalised Linear Models (GLMs) [59][21] are also used in various problems among the literature [60[22][23],61], while Generalised Additive Models (GAMs), an extension of these, allow the modelling of non-linear relationships and are used for prediction in medical problems as well [62,63][24][25]. Decision trees are considered transparent models because of their hierarchical structure which allows the easy visualisation of the logical processing of data in decision making processes. Moreover, a set of rules can be extracted to formalise that interpretation. They can be used for classification in the medical context [64[26][27],65], however, they sometimes show poor generalisation capabilities, so it is most common to use tree ensembles (like the random forest algorithm [66][28]) that show better performance, in combination with post hoc explainability methods, as they lose some interpretability [67,68,69,70][29][30][31][32]. The generalisation of formal models through Bayesian networks [71][33], have become popular for modelling medical prediction problems [72[34][35][36][37][38],73,74,75,76], representing conditional dependencies between variables in the form of a graph, so that evidence can be propagated through the network to update the diagnostic or prognostic states of a patient [77][39]. This reasoning process can be easily visualised in a straightforward manner. Interpretable models can be used by themselves, but another interesting strategy is using them in ensemble models. Ensemble models consist of combining several different ML methods to achieve a better performance and better interpretability than with a black-box model alone [78][40]. These approaches can also include these interpretable models in conjunction with DL models such as neural networks [79,80[41][42][43][44],81,82], as well as other post hoc explainability techniques [83,84][45][46]. However, they pose increasingly, and as yet unresolved, complex interpretation issues, as recently emphasised by Pearl [85][47].

2.3. Interpretation of Neural Network Architectures

Despite the fact that neural networks cannot be fully included in the category of intrinsically interpretable models, it can characterize them (DL are also included), such as architectures designed so that they resemble some of the simple neural modelling of brain function and that are used heuristically to recognise images or perform different tasks, and some neural network architectures have been specifically designed to provide interpretability. The first type tries to mimic human decision-making where the decision is based on previously seen examples. In reference [86][48], a prototype learning design is presented to provide the interpretable samples associated with the different types of respiratory sounds (normal, crackle, and wheeze). This technique learns a set of prototypes in a latent space that are used to make a prediction. Moreover, it also allows for a new sample to be compared with the set of prototypes, identifying the most similar and decoding it to its original input representation. The architecture is based on the work in reference [87][49] and it intrinsically provides an automatic process to extract the input characteristics that are related to the associated prototype given that input. Other methods’ main motivation is to behave in a way more similar to how clinicians diagnose, and provide explanations in the form of relevant features. Among this type, attention maps are widely used. In short, they extract the influence of a feature on the output for a given sample. They are based on the gradients of the learned model and, in [88][50], have been used to provide visual MRI explanations of liver lesions. For small datasets, it is even possible to include some kind of medical knowledge as structural constraint rules over the attention maps during the process design [89][51]. Moreover, the attention maps can also be applied at different scales, concatenating feature maps, as proposed in reference [90][52], and being able to identify small structures on retina images. These approaches are specific to DL but, still, surrogate models or post hoc methods are applicable to add explainability.

3. Post Hoc Explainability Methods

Extending the above approach to transparency came with the development of more complex data-based ML methods, such as support vector machines (SVMs), tree ensembles, and, of course, DL techniques. The latter have become popular due to their impressive performance on a huge variety of tasks, sometimes even surpassing human accuracy for concrete applications, but also unfortunately entailing deeper opacity, for instance, than the detailed explanations that classic statistics can provide. For this reason, different explainability methods have been proposed in order to shed light on the inner workings or algorithmic implementations used in these black-box-like AI models. Because they are implemented as added facilities to these models, executed either over the results or the finished models, they are known as post hoc methods, which produce post hoc explanations, as opposed to the approach of intrinsically interpretable models. Many of the approaches included in this category, which are also currently the most widely used, as reported in the literature, are model agnostic. Post hoc model agnostic methods are so popular due to their convenience: they are quick and easy to set up, flexible, and well-established. Within this category, there are also some model specific post hoc techniques designed to work only for a particular type of model. These are less flexible, but tend to be faster and sometimes more accurate due to their specificity, as they can access the model internals and can produce different types of explanations that might be more suitable for some cases [30][4]. Regardless of their range of application, post hoc methods can also be grouped on the basis of their functionalities. Combining the taxonomies proposed in references [11][53] and [67][29], it can broadly differentiate between explanations through simplification (surrogate models), feature relevance methods, visualisation techniques, and example-based explanations. In the following sections, these ideas will be presented as well as some of the most popular and representative methods belonging to each group.

3.1. Explanation by Simplification

One way to explain a black-box model is to use a simpler, intrinsically interpretable model for the task of explaining its behaviour. One method that uses this idea, which is undoubtedly one of the most employed ones throughout all the literature, is LIME (Local Interpretable Model-agnostic Explanations) [91][54]. This method builds a simple linear surrogate model to explain each of the predictions of the learned black-box model. The prediction’s input to be explained is locally perturbed creating a new dataset that is used to build the explainable surrogate model. An explanation of instances can help to enforce trust in assisted AI clinical diagnosis within a patient diagnosis workflow [92][55]. Knowledge distillation is another technique included in this category. It was developed to compress neural networks for efficiency purposes, but it can also be used to construct a global surrogate interpretable model [93][56]. It consists of using the more complex black-box model as a “teacher” for a simpler model that learns to mimic its output scores. If the “student” model demonstrates sufficient empirical performance, a domain expert may even prefer to use it in place of the teacher model and LIME. The main rationale behind this type of modelling is the assumption that some potential noise and error in the training data may affect the training efficacy of simple models. The authors of reference [94][57] used knowledge distillation to create an interpretable model, achieving a strong prediction performance for ICU outcome prediction. Under this category, weit could also include techniques that attempt to simplify the models by extracting knowledge in a more comprehensive way. For example, rule extraction methods try to approximate the decision-making process of the black-box model, such as a neural network, with a set of rules or decision trees. Some of the methods try decomposing the units of the model to extract these rules [95][58], while others keep treating the original model as a black box and use the outcomes to perform a rule search [96][59]. There are also combinations of both approaches [97][60].

3.2. Explanation Using Feature Relevance Methods

In the category of feature relevance methods, it can find many popular examples of explainability techniques. These approaches try to find the most relevant variables or features to the model’s predictions, those that most influence the outcome in each case or in general. The ancestry to these techniques can be found in both statistical and heuristic approaches dating back to the 1930s with Principal Component Analysis (PCA), which explains the weightings of features, or contributions to relevance in terms of their contribution to inter- and intra-population patterns of multinomial variance and covariance [98][61]. These techniques were also shown to be central to both dimensionality reduction and its explanation in terms of information content for pattern recognition [99][62] and clinical diagnostic classification and prediction using subspace methods from atomic logic [100][63]. Later, related techniques for feature extraction by projection pursuit were developed and applied to clinical decision-making. More recently, with LIME (that could also be included in this group), SHAP (SHapley Additive exPlanations) is one of the most widely used XAI model agnostic techniques, and it is the main example of the category of feature relevance methods. It is based on concepts from game theory that allow the computing, which are the features that contribute the most to the outcomes of the black-box model, by trying different feature set permutations [101][64]. SHAP explanations increase trust by helping to test prior knowledge and can also help to get insights into new ones [102][65]. Other well-known similar examples that measure the importance of different parts of the input by trying different changes is SA (Sensitivity Analysis) [103][66], and LRP (Layer-Wise Relevance Propagation) [104][67]. Deep Taylor Decomposition (an evolution of LRP) [105][68] and DeepLIFT [106][69] are other model-specific alternatives for neural networks, that propagate the activation of neurons with respect to the inputs to compute feature importance.

3.3. Explanation by Visualisation Techniques

Some of the aforementioned methods can produce visual explanations in some cases. Still, some other methods that directly visualize the inner workings of the models, like Grad-CAM [107][70], that helps in showing the activation of the layers of a convolutional neural network. In addition, there are other techniques that visualize the inputs and outputs of a model and the relationship between them, such as PDP (Partial Dependence Plots) [83][45] and ICE (Individual Conditional Expectation) plots [108][71]. It is worth mentioning that visualisation can help to build explicable interfaces to interact with users, but it is complex to use them as an automatic step of the general explainability process.

3.4. Explanations by Examples

Finally, another approach to produce explanations is to provide examples of other similar cases that help in understanding why one instance has been classified as one object or structure or another by the model, or instead, dissimilar instances (counterfactuals) that might provide insights as to why not. For instance, MMD-critic [109][72] is an unsupervised algorithm that finds prototypes (the most representative instances of a class) as well as criticisms (instances that belong to a class but are not well represented by the prototypes). Another example are counterfactual explanations [110][73] that describe the minimum conditions that would lead to a different prediction by the model.

4. Evaluation of Explainability

Despite the growing body of literature on different XAI methods, and the rising interest in the topics of interpretability, explainability, and transparency, there is still limited research on the field of formal evaluations and measurements for these issues [111][74]. Most studies just employ XAI techniques without providing any kind of quantitative evaluation or appraisal of whether the produced explanations are appropriate. Developing formal metrics and a more systematic evaluation of different methods can be difficult because of the variety of the available techniques and the lack of consensus on the definition of interpretability [112][75]. Moreover, contrary to usual performance metrics, there is no ground-truth when evaluating explanations of a black-box model [27,112][75][76]. However, this is a foundational work of great importance, as such evaluation metrics would help towards not only assessing the quality of explanations and somehow measuring if the goal of interpretability is met, but also to compare between techniques and help standardise the different approaches, making it easier to select the most appropriate method for each case [113][77]. In short, there is a need for more robust metrics, standards, and methodologies that help data scientists and engineers to integrate interpretability in medical AI applications in a more detailed, verified, consistent, and comparable way, along the whole methodology, design, and algorithmic development process [114][78]. Nevertheless, in the few studies available on this topic, there are some common aspects that establish a starting point for further development, and there are some metrics, such as the robustness, consistency, comprehensibility, and importance of explanations. A good and useful explanation for an AI model is one that is in accordance with human intuition and easy to understand [115][79]. To evaluate this, some qualitative and quantitative intuitions have already been proposed.
  • On the one hand, qualitative intuitions include notions about the cognitive form, complexity, and structure of the explanation. For example, what are the basic units that compose the explanation and how many are there (more units mean more complexity), how are they related (rules or hierarchies might be more interpretable for humans), if any uncertainty measure is provided or not, and so on [111][74].
  • On the other hand, quantitative intuitions are easier to formally measure and include, for example, notions like identity (for identical instances, explanations should be the same), stability (instances from the same class should have comparable explanations) or separability (distinct instances should have distinct explanations) [115,116][79][80]. The metrics based on these intuitions mathematically measure the similarity between explanations and instances as well as the agreement between the explainer and the black-box model.
Other options to evaluate XAI techniques include factors such as the time needed to output an explanation or the ability to detect bias in the data [115][79]. Another interesting strategy is to quantify the overlap between human intuitions (such as expert annotations) and the explanations obtained [117[81][82],118], or using human ratings by experts on the topic [113,119,120,121][77][83][84][85]. There are also different options regarding the context in which these various metrics can be used. The evaluation of an XAI system can be made either in the context of the final target task with the help of domain experts, in simpler tasks, or using formal definitions [111][74]. Depending on the specific characteristics of the problem and available resources, different approaches and metrics can be chosen.

References

  1. Stiglic, G.; Kocbek, P.; Fijacko, N.; Zitnik, M.; Verbert, K.; Cilar, L. Interpretability of machine learning-based prediction models in healthcare. Wiley Interdiscip. Rev.-Data Min. Knowl. Discov. 2020, 10, e1379.
  2. Singh, A.; Sengupta, S.; Lakshminarayanan, V. Explainable Deep Learning Models in Medical Image Analysis. J. Imaging 2020, 6, 52.
  3. Vilone, G.; Longo, L. Classification of explainable artificial intelligence methods through their output formats. Mach. Learn. Knowl. Extr. 2021, 3, 615–661.
  4. Abdullah, T.; Zahid, M.; Ali, W. A Review of Interpretable ML in Healthcare: Taxonomy, Applications, Challenges, and Future Directions. Symmetry 2021, 13, 2439.
  5. Biran, O.; Cotton, C. Explanation and justification in machine learning: A survey. In Proceedings of the IJCAI-17 Workshop on Explainable AI (XAI), Melbourne, Australia, 19–25 August 2017; Volume 8, pp. 8–13.
  6. Preece, A. Asking ‘Why’ in AI: Explainability of intelligent systems–perspectives and challenges. Intell. Syst. Account. Financ. Manag. 2018, 25, 63–72.
  7. Vourgidis, I.; Mafuma, S.J.; Wilson, P.; Carter, J.; Cosma, G. Medical expert systems—A study of trust and acceptance by healthcare stakeholders. In Proceedings of the UK Workshop on Computational Intelligence, Nottingham, UK, 5–7 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 108–119.
  8. Shortliffe, E.H.; Davis, R.; Axline, S.G.; Buchanan, B.G.; Green, C.C.; Cohen, S.N. Computer-based consultations in clinical therapeutics: Explanation and rule acquisition capabilities of the MYCIN system. Comput. Biomed. Res. 1975, 8, 303–320.
  9. Weiss, S.M.; Kulikowski, C.A.; Amarel, S.; Safir, A. A model-based method for computer-aided medical decision-making. Artif. Intell. 1978, 11, 145–172.
  10. Miller, R.A.; Pople, H.E., Jr.; Myers, J.D. Internist-I, an experimental computer-based diagnostic consultant for general internal medicine. In Computer-Assisted Medical Decision Making; Springer: Berlin/Heidelberg, Germany, 1985; pp. 139–158.
  11. Long, W.; Naimi, S.; Criscitiello, M.; Pauker, S.; Szolovits, P. An aid to physiological reasoning in the management of cardiovascular disease. In Proceedings of the 1984 Computers in Cardiology Conference, IEEE Computer Society, Long Beach, CA, USA, 14–18 February 1984; pp. 3–6.
  12. Clancey, W.J.; Shortliffe, E.H. Readings in Medical Artificial Intelligence: The First Decade; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1984.
  13. Ford, K.M.; Coffey, J.W.; Cañas, A.; Andrews, E.J. Diagnosis and explanation by a nuclear cardiology expert system. Int. J. Expert Syst. 1996, 9, 4.
  14. Hogan, W.R.; Wagner, M.M. The use of an explanation algorithm in a clinical event monitor. In Proceedings of the AMIA Symposium. American Medical Informatics Association, Washington, DC, USA, 6–10 November 1999; p. 281.
  15. Darlington, K. Using explanation facilities in healthcare expert systems. In Proceedings of the HEALTHINF 2008: Proceedings of the First International Conference on Health Informatics, Funchal, Madeira, Portugal, 28–31 January 2008; Volume 1.
  16. Darlington, K.W. Designing for explanation in health care applications of expert systems. Sage Open 2011, 1, 2158244011408618.
  17. Rennels, G.D.; Shortliffe, E.H.; Miller, P.L. Choice and explanation in medical management: A multiattribute model of artificial intelligence approaches. Med. Decis. Mak. 1987, 7, 22–31.
  18. Molino, G.; Console, L.; Torasso, P. Causal expert systems supporting medical decision making and medical education: Explanations based on simulated situations. In Proceedings of the Images of the Twenty-First Century, Annual International Engineering in Medicine and Biology Society; IEEE: Seattle, WA, USA, 1989; pp. 1827–1828.
  19. Ledley, R.S.; Lusted, L.B. Reasoning foundations of medical diagnosis: Symbolic logic, probability, and value theory aid our understanding of how physicians reason. Science 1959, 130, 9–21.
  20. Jacquez, J. The Diagnostic Process: Proceedings of a Conference Held at the University of Michigan; Malloy Lithographing, Inc.: Ann Arbor, MI, USA, 1963.
  21. Nelder, J.A.; Wedderburn, R.W. Generalized linear models. J. R. Stat. Soc. Ser. A 1972, 135, 370–384.
  22. Meacham, S.; Isaac, G.; Nauck, D.; Virginas, B. Towards explainable AI: Design and development for explanation of machine learning predictions for a patient readmittance medical application. In Proceedings of the Intelligent Computing-Proceedings of the Computing Conference, London, UK, 16–17 July 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 939–955.
  23. Banegas-Luna, A.J.; Peña-García, J.; Iftene, A.; Guadagni, F.; Ferroni, P.; Scarpato, N.; Zanzotto, F.M.; Bueno-Crespo, A.; Pérez-Sánchez, H. Towards the interpretability of machine learning predictions for medical applications targeting personalised therapies: A cancer case survey. Int. J. Mol. Sci. 2021, 22, 4394.
  24. Karatekin, T.; Sancak, S.; Celik, G.; Topcuoglu, S.; Karatekin, G.; Kirci, P.; Okatan, A. Interpretable machine learning in healthcare through generalized additive model with pairwise interactions (GA2M): Predicting severe retinopathy of prematurity. In Proceedings of the 2019 International Conference on Deep Learning and Machine Learning in Emerging Applications (Deep-ML), Boca Raton, FL, USA, 26–28 August 2019; IEEE: New York City, NY, USA, 2019; pp. 61–66.
  25. Wang, H.; Huang, Z.; Zhang, D.; Arief, J.; Lyu, T.; Tian, J. Integrating co-clustering and interpretable machine learning for the prediction of intravenous immunoglobulin resistance in kawasaki disease. IEEE Access 2020, 8, 97064–97071.
  26. Itani, S.; Rossignol, M.; Lecron, F.; Fortemps, P. Towards interpretable machine learning models for diagnosis aid: A case study on attention deficit/hyperactivity disorder. PLoS ONE 2019, 14, e0215720.
  27. Brito-Sarracino, T.; dos Santos, M.R.; Antunes, E.F.; de Andrade Santos, I.B.; Kasmanas, J.C.; de Leon Ferreira, A.C.P. Explainable machine learning for breast cancer diagnosis. In Proceedings of the 2019 8th Brazilian Conference on Intelligent Systems (BRACIS), Salvador, Brazil, 15–18 October 2019; IEEE: New York City, NY, USA, 2019; pp. 681–686.
  28. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32.
  29. Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115.
  30. Mattogno, P.P.; Caccavella, V.M.; Giordano, M.; D’Alessandris, Q.G.; Chiloiro, S.; Tariciotti, L.; Olivi, A.; Lauretti, L. Interpretable Machine Learning–Based Prediction of Intraoperative Cerebrospinal Fluid Leakage in Endoscopic Transsphenoidal Pituitary Surgery: A Pilot Study. J. Neurol. Surg. Part Skull Base 2022, 83, 485–495.
  31. Alsinglawi, B.; Alshari, O.; Alorjani, M.; Mubin, O.; Alnajjar, F.; Novoa, M.; Darwish, O. An explainable machine learning framework for lung cancer hospital length of stay prediction. Sci. Rep. 2022, 12, 607.
  32. El-Sappagh, S.; Alonso, J.M.; Islam, S.; Sultan, A.M.; Kwak, K.S. A multilayer multimodal detection and prediction model based on explainable artificial intelligence for Alzheimer’s disease. Sci. Rep. 2021, 11, 2660.
  33. Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: Cambridge, MA, USA, 1988.
  34. Chang, C.C.; Cheng, C.S. A Bayesian decision analysis with fuzzy interpretability for aging chronic disease. Int. J. Technol. Manag. 2007, 40, 176–191.
  35. Casini, L.; McKay Illari, P.; Russo, F.; Williamson, J. Recursive Bayesian nets for prediction, explanation and control in cancer science. Theoria 2011, 26, 495–4548.
  36. Kyrimi, E.; Marsh, W. A progressive explanation of inference in ‘hybrid’ Bayesian networks for supporting clinical decision making. In Proceedings of the Conference on Probabilistic Graphical Models. PMLR, Lugano, Switzerland, 6 September 2016; pp. 275–286.
  37. Xie, W.; Ji, M.; Zhao, M.; Zhou, T.; Yang, F.; Qian, X.; Chow, C.Y.; Lam, K.Y.; Hao, T. Detecting symptom errors in neural machine translation of patient health information on depressive disorders: Developing interpretable bayesian machine learning classifiers. Front. Psychiatry 2021, 12, 771562.
  38. Yun, J.; Basak, M.; Han, M.M. Bayesian rule modeling for interpretable mortality classification of COVID-19 patients. Cmc-Comput. Mater. Continua 2021, 2827–2843.
  39. Kyrimi, E.; Mossadegh, S.; Tai, N.; Marsh, W. An incremental explanation of inference in Bayesian networks for increasing model trustworthiness and supporting clinical decision making. Artif. Intell. Med. 2020, 103, 101812.
  40. Kanda, E.; Epureanu, B.I.; Adachi, T.; Tsuruta, Y.; Kikuchi, K.; Kashihara, N.; Abe, M.; Masakane, I.; Nitta, K. Application of explainable ensemble artificial intelligence model to categorization of hemodialysis-patient and treatment using nationwide-real-world data in Japan. PLoS ONE 2020, 15, e0233491.
  41. Chen, J.; Dai, X.; Yuan, Q.; Lu, C.; Huang, H. Towards interpretable clinical diagnosis with Bayesian network ensembles stacked on entity-aware CNNs. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 3143–3153.
  42. Ahmed, Z.U.; Sun, K.; Shelly, M.; Mu, L. Explainable artificial intelligence (XAI) for exploring spatial variability of lung and bronchus cancer (LBC) mortality rates in the contiguous USA. Sci. Rep. 2021, 11, 24090.
  43. Singh, R.K.; Pandey, R.; Babu, R.N. COVIDScreen: Explainable deep learning framework for differential diagnosis of COVID-19 using chest X-rays. Neural Comput. Appl. 2021, 33, 8871–8892.
  44. Yu, T.H.; Su, B.H.; Battalora, L.C.; Liu, S.; Tseng, Y.J. Ensemble modeling with machine learning and deep learning to provide interpretable generalized rules for classifying CNS drugs with high prediction power. Briefings Bioinform. 2022, 23, bbab377.
  45. Peng, J.; Zou, K.; Zhou, M.; Teng, Y.; Zhu, X.; Zhang, F.; Xu, J. An explainable artificial intelligence framework for the deterioration risk prediction of hepatitis patients. J. Med. Syst. 2021, 45, 61.
  46. Kim, S.H.; Jeon, E.T.; Yu, S.; Oh, K.; Kim, C.K.; Song, T.J.; Kim, Y.J.; Heo, S.H.; Park, K.Y.; Kim, J.M.; et al. Interpretable machine learning for early neurological deterioration prediction in atrial fibrillation-related stroke. Sci. Rep. 2021, 11, 20610.
  47. Pearl, J.; Mackenzie, D. The Book of Why: The New Science of Cause and Effect; Hachette Basic Books: New York City, NY, USA, 2018.
  48. Ren, Z.; Nguyen, T.T.; Nejdl, W. Prototype learning for interpretable respiratory sound analysis. In Proceedings of the ICASSP 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 9087–9091.
  49. Li, O.; Liu, H.; Chen, C.; Rudin, C. Deep learning for case-based reasoning through prototypes: A neural network that explains its predictions. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32.
  50. Wan, Y.; Zheng, Z.; Liu, R.; Zhu, Z.; Zhou, H.; Zhang, X.; Boumaraf, S. A Multi-Scale and Multi-Level Fusion Approach for Deep Learning-Based Liver Lesion Diagnosis in Magnetic Resonance Images with Visual Explanation. Life 2021, 11, 582.
  51. Xu, Y.; Hu, M.; Liu, H.; Yang, H.; Wang, H.; Lu, S.; Liang, T.; Li, X.; Xu, M.; Li, L.; et al. A hierarchical deep learning approach with transparency and interpretability based on small samples for glaucoma diagnosis. NPJ Digit. Med. 2021, 4, 48.
  52. Liao, W.; Zou, B.; Zhao, R.; Chen, Y.; He, Z.; Zhou, M. Clinical interpretable deep learning model for glaucoma diagnosis. IEEE J. Biomed. Health Inform. 2019, 24, 1405–1412.
  53. Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160.
  54. Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Cconference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144.
  55. Magesh, P.R.; Myloth, R.D.; Tom, R.J. An explainable machine learning model for early detection of Parkinson’s disease using LIME on DaTSCAN imagery. Comput. Biol. Med. 2020, 126, 104041.
  56. Tan, S.; Caruana, R.; Hooker, G.; Lou, Y. Distill-and-compare: Auditing black-box models using transparent model distillation. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, New Orleans, LA, USA, 2–3 February 2018; pp. 303–310.
  57. Che, Z.; Purushotham, S.; Khemani, R.; Liu, Y. Interpretable deep models for ICU outcome prediction. In Proceedings of the AMIA annual symposium proceedings. American Medical Informatics Association, Chicago, IL, USA, 16 November 2016; Volume 2016, p. 371.
  58. Krishnan, R.; Sivakumar, G.; Bhattacharya, P. A search technique for rule extraction from trained neural networks. Pattern Recognit. Lett. 1999, 20, 273–280.
  59. Etchells, T.A.; Lisboa, P.J. Orthogonal search-based rule extraction (OSRE) for trained neural networks: A practical and efficient approach. IEEE Trans. Neural Netw. 2006, 17, 374–384.
  60. Barakat, N.; Diederich, J. Eclectic rule-extraction from support vector machines. Int. J. Comput. Intell. 2005, 2, 59–62.
  61. Fisher, R.A. The logic of inductive inference. J. R. Stat. Soc. 1935, 98, 39–82.
  62. Kaminuma, T.; Takekawa, T.; Watanabe, S. Reduction of clustering problem to pattern recognition. Pattern Recognit. 1969, 1, 195–205.
  63. Kulikowski, C.A. Pattern recognition approach to medical diagnosis. IEEE Trans. Syst. Sci. Cybern. 1970, 6, 173–178.
  64. Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777.
  65. Weis, C.; Cuénod, A.; Rieck, B.; Dubuis, O.; Graf, S.; Lang, C.; Oberle, M.; Brackmann, M.; Søgaard, K.K.; Osthoff, M.; et al. Direct antimicrobial resistance prediction from clinical MALDI-TOF mass spectra using machine learning. Nat. Med. 2022, 28, 164–174.
  66. Saltelli, A. Sensitivity analysis for importance assessment. Risk Anal. 2002, 22, 579–590.
  67. Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 10, e0130140.
  68. Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.R. Explaining nonlinear classification decisions with deep taylor decomposition. Pattern Recognit. 2017, 65, 211–222.
  69. Shrikumar, A.; Greenside, P.; Kundaje, A. Learning important features through propagating activation differences. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 3145–3153.
  70. Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626.
  71. Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 2015, 24, 44–65.
  72. Kim, B.; Khanna, R.; Koyejo, O.O. Examples are not enough, learn to criticize! criticism for interpretability. Adv. Neural Inf. Process. Syst. 2016, 29.
  73. Wachter, S.; Mittelstadt, B.; Russell, C. Counterfactual explanations without opening the black box: Automated decisions and the GDPR. Harv. JL Tech. 2017, 31, 841.
  74. Doshi-Velez, F.; Kim, B. Considerations for Evaluation and Generalization in Interpretable Machine Learning. In Explainable and Interpretable Models in Computer Vision and Machine Learning. The Springer Series on Challenges in Machine Learning; Springer: Cham, Switzerland, 2018.
  75. Markus, A.; Kors, J.; Rijnbeek, P. The role of explainability in creating trustworthy artificial intelligence for health care: A comprehensive survey of the terminology, design choices, and evaluation strategies. J. Biomed. Inform. 2021, 113, 103655.
  76. Lipton, Z.C. The Mythos of Model Interpretability: In machine learning, the concept of interpretability is both important and slippery. Queue 2018, 16, 31–57.
  77. Kaur, D.; Uslu, S.; Durresi, A.; Badve, S.; Dundar, M. Trustworthy Explainability Acceptance: A New Metric to Measure the Trustworthiness of Interpretable AI Medical Diagnostic Systems. Complex Intell. Softw. Intensive Syst. 2021, 278.
  78. Kolyshkina, I.; Simoff, S. Interpretability of Machine Learning Solutions in Public Healthcare: The CRISP-ML Approach. Front. Big Data 2021, 4, 660206.
  79. ElShawi, R.; Sherif, Y.; Al-Mallah, M.; Sakr, S. Interpretability in healthcare: A comparative study of local machine learning interpretability techniques. Comput. Intell. 2021, 37, 1633–1650.
  80. Honegger, M.R. Shedding light on black box machine learning algorithms: Development of an axiomatic framework to assess the quality of methods that explain individual predictions. arXiv 2018, arXiv:1808.05054.
  81. Muddamsetty, S.M.; Jahromi, M.N.; Moeslund, T.B. Expert level evaluations for explainable AI (XAI) methods in the medical domain. In Proceedings of the International Conference on Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 35–46.
  82. de Souza, L.; Mendel, R.; Strasser, S.; Ebigbo, A.; Probst, A.; Messmann, H.; Papa, J.; Palm, C. Convolutional Neural Networks for the evaluation of cancer in Barrett’s esophagus: Explainable AI to lighten up the black-box. Comput. Biol. Med. 2021, 135, 104578.
  83. Kumarakulasinghe, N.B.; Blomberg, T.; Liu, J.; Leao, A.S.; Papapetrou, P. Evaluating local interpretable model-agnostic explanations on clinical machine learning classification models. In Proceedings of the 2020 IEEE 33rd International Symposium on Computer-Based Medical Systems (CBMS), Rochester, MN, USA, 28–30 July 2020; pp. 7–12.
  84. Singh, A.; Balaji, J.; Rasheed, M.; Jayakumar, V.; Raman, R.; Lakshminarayanan, V. Evaluation of Explainable Deep Learning Methods for Ophthalmic Diagnosis. Clin. Ophthalmol. 2021, 15, 2573–2581.
  85. Deperlioglu, O.; Kose, U.; Gupta, D.; Khanna, A.; Giampaolo, F.; Fortino, G. Explainable framework for Glaucoma diagnosis by image processing and convolutional neural network synergy: Analysis with doctor evaluation. Future Gener. Comput. Syst. 2022, 129, 152–169.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback