Flash-Boiling Atomization: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Catherine Yang and Version 1 by Tali Bar-Kohany.

Flash-boiling atomization is a method by which a liquid is brought into a superheated state, such as vigorous boiling, in a short timeframe while the bubbles grow considerably fast. This leads to the disintegration of the continuous liquid into tiny droplets. Flash-boiling, effervescent, and air-assisted atomization are based on a two-phase flow to achieve effective atomization. 

  • flash boiling
  • spray
  • atomization
  • fuel injection
  • cavitation
  • depressurization

1. Flash Boiling

Flash boiling occurs when the liquid is forced to reach a metastable superheated state via a rapid pressure drop that is well below its saturation pressure (grey area in Figure 1). Under these conditions, vapor bubble nucleation occurs, which leads to the formation of bubbles, their growth, and, subsequently, the breaking down of the liquid’s continuous phase into a fine spray. All in a very short time.
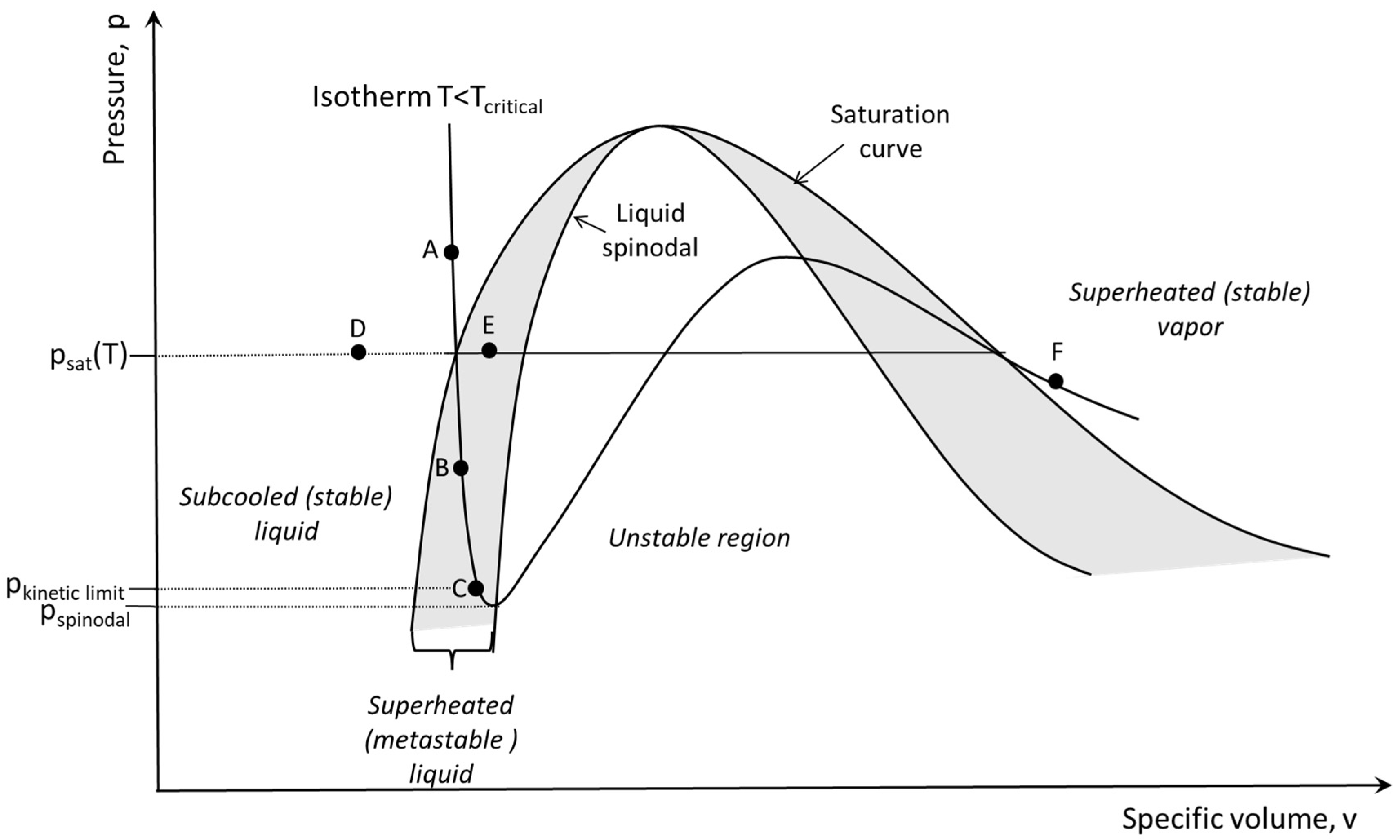
Figure 1.
Typical pressure–volume phase diagram, indicating a subcritical isotherm (Bar-Kohany et al. Energies, 2023).
Reaching a metastable superheated state can be achieved through many different pathways. It is commonly accepted to divide these multiple paths into either isothermal depressurization (AB in Figure 1) or isobaric heating (DE in Figure 1), where the first is commonly used in practical spray generation systems [1] and is the focus of this present article.
The flash-boiling process, therefore, involves a rapid phase change in the liquid. Phase change via nucleation occurs once the superheated liquid encounters disturbances that are larger than the critical disturbance appropriate to its degree of superheating. Homogeneous nucleation at the kinetic limit (point C in Figure 1) occurs when the fluctuations serve as the critical disturbance on the verge of the spinodal curve [2]. It is, however, more likely that heterogeneous nucleation rather than homogeneous nucleation is the dominant mechanism in flash-boiling atomization processes because, in most commercial applications, depressurization is not fast enough to overcome the existing disturbances. The disturbances are developed almost instantaneously at nucleation sites that are usually present in dissolved gases, impurities, colloids, or surface roughness, which can be found almost everywhere in practical systems. In a homogeneous nucleation regime, pressure fluctuations at the molecular level form the nucleation centers. If the superheated liquid relaxes to finite-sized bubbles, it relaxes into superheated vapor (point F in Figure 1) to fulfill the equilibrium condition of equal chemical potentials in the liquid and vapor phases [3].
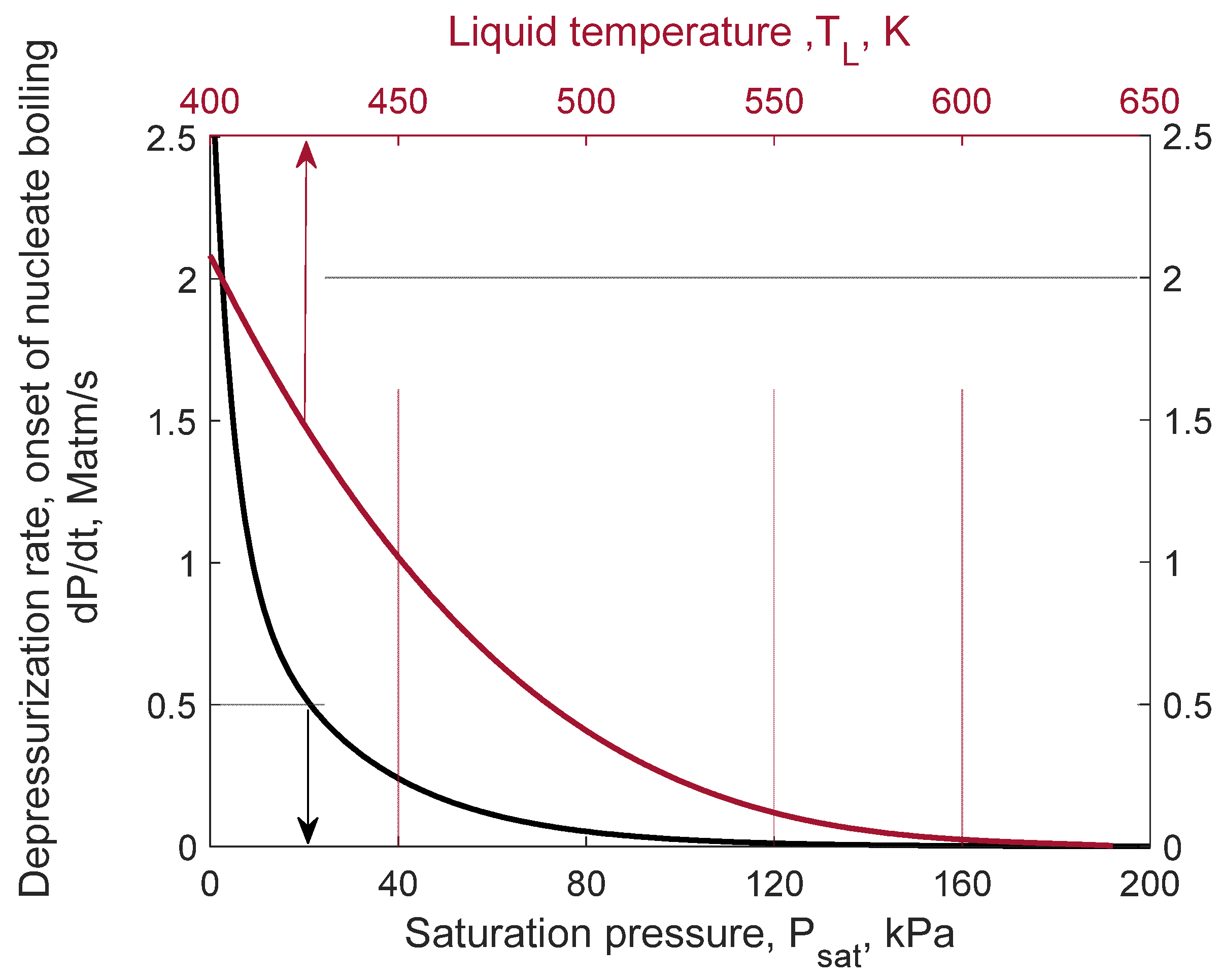
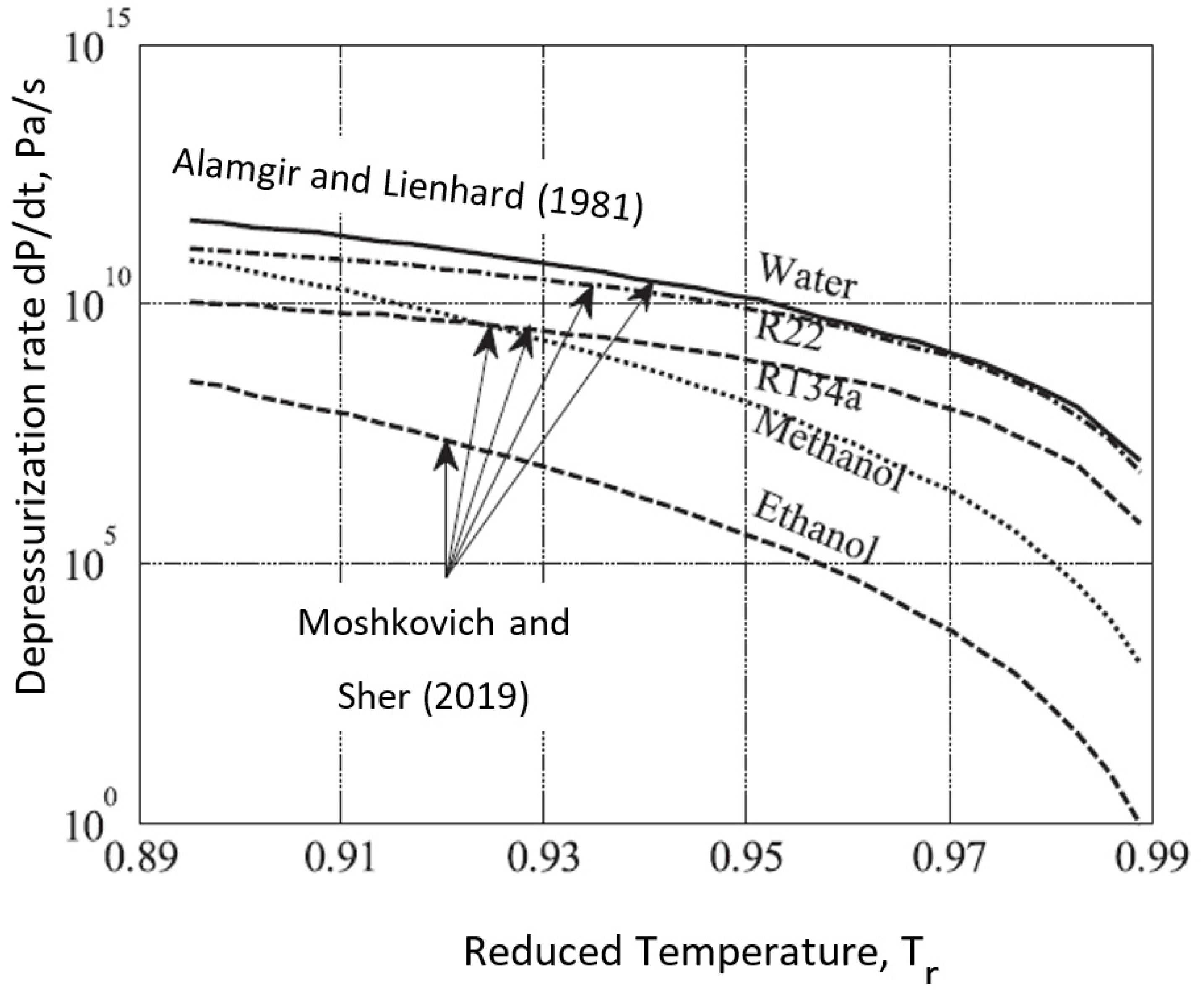
Despite the abundance of nucleation sites available in spraying processes, rapid processes can lead to near-spinodal degrees of superheating, depending on the degree of contamination of the fluid (colloids, dissolved gases, etc.) and the depressurization or heating rate (a few examples can be found in [2][4][5][6][7][8][9][10]). The spinodal (or kinetic limit, point C in Figure 1) pressure values may be negative (negative absolute pressures) for most operating conditions in some common applications, e.g., engines and pharmaceuticals, making it more challenging to reach spinodal limits in depressurization processes [11]. A few models were devised to predict the degree of superheating in the rapid depressurization of water in one atmosphere [12][13][14][15]. Figure 2 presents the minimal depressurization rate for which the kinetic stability conditions are met. The results are compared to the experimental results of Alamgir and Lienhard for water [12].
Figure 2. Minimal depressurization rate for which the kinetic stability conditions are reached vs. the initial reduced temperature, as predicted by Alamgir and Lienhard [12] and Moshkovich and Sher [15] (modified from Moshkovich and Sher [15]).
The quality of spray is heavily influenced by the number of nucleation sites and the degree of superheating, which plays a significant role in determining the dimension of the active nucleation sites and the size of the initial bubbles. The number of nucleation sites determines the number of bubbles. When the two-phase mixture of liquid and bubbles flow either through a single or a twin orifice injector [16], it determines the relative velocities of the two phases, thus the shearing forces, and, therefore, ultimately affecting the effectiveness of secondary breakup mechanisms [17].
The stochastic nature of the nucleation affects the spray characteristics. Therefore, a more thorough understanding of the effects of the following main topics on the nucleation conditions in pure liquids, liquid solutions, fuel surrogates [18], and nano-fluids should still be pursued:
  • Depressurization rate;
  • Wettability;
  • Nano-bubbles;
  • Trans-critical conditions;
  • Negative nucleation pressure.

2. Atomization Mechanisms Following Flash-Boiling

2.1. Bubble Growth

Immediately after the formation of stable vapor embryos via nucleation events, bubble growth, and primary and secondary breakup occur [17][19]. A larger degree of superheat implies a larger driving force for bubble growth, as manifested by the Jakob number, in both the inertial and the heat-diffusion regimes [20][21]. The general behavior of bubble growth can be described by: Rb~tm, where Rb is the bubble radius, m is an exponential growth parameter, and t is the time. For a homogeneous growth within a uniformly superheated liquid, it was shown by Rayleigh that during the initial period of growth, the inertial regime, m = 1. Plesset and Zwick showed that the heat-diffusion regime’s asymptotic behavior can be presented as Rb~t1/2 [22]. For a heterogeneous growth, this parameter is usually determined empirically. Recent studies found that its value can vary between 0.1 and 0.6 and that it is reduced as the pressure increases [23]. The empirical constant, m, can vary considerably, depending on the fluids and other conditions such as bubble–liquid relative motion [20] and subcooling degrees.
To study bubble growth behavior in time-dependent fields, the variation in the vapor temperature should be considered. Recently, it was found that assuming constant saturation pressure may lead to over-prediction of the growth rate at lower to intermediate Jakob numbers [24]. Jones and Zuber [25] were among the first who analyzed the process and found that the bubble growth rate increases as Rb~tn+1/2, which is faster than the heat-diffusion regime’s asymptotic behavior.
The flash-boiling atomization of composite droplets deviates from the classical behavior of a bubble in an infinite liquid medium since the pressure inside the bubble increases faster than within the confining droplet [8]. Thus, the growth rate of the bubble within the confining droplet was shown to lay somewhere between the maximal limit of the initial inertial regime and the lower limit of the heat diffusion regime, as shown in Figure 3a. The quasi-steady approach could be employed if the thermal boundary layer, δ, is still within the confining droplet (Rδ < Rs) and is thinner than the bubble radius (=(Rδ − Rb)/Rb << 1, as shown in Figure 3b). Following Avedisian’s approach [26] that analyzed the case for bubble growth following the heating of a droplet, Figure 3b,c present the variation in the pressure field for bubble growth following the depressurization of the droplet. Bubble growth within a finite medium is subjected to asymmetric conditions. Shusser et al. [8] showed that if the bubble does not deviate by more than 25% from the center of the confining droplet, then it can be assumed that the bubble growth expressions, developed for a concentric bubble, will lead to an error of 10% at most. Considering other confining geometries with flexible or rigid boundaries, such as micro-channels, raises the question of how the varying pressure fields and the location of the bubble in a micro-channel influence its growth rate.
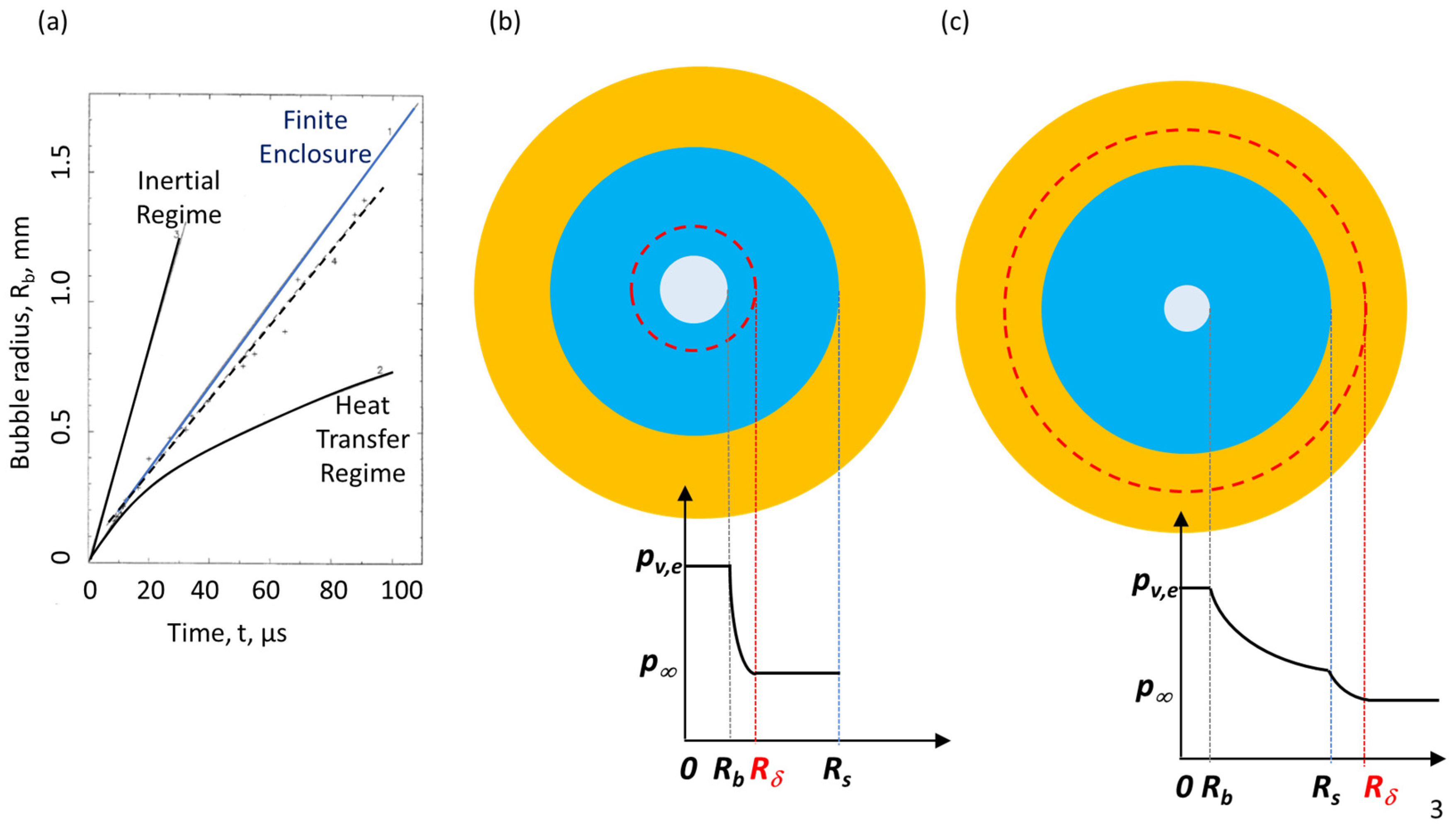
Figure 3. (a) Bubble growth within water as a function of time; solid black curves represent the growth predicted via the inertial and heat transfer regimes in an infinite medium, and the solid blue curve represents the predicted growth in a confining water droplet by Shusser et al. [8], and the dashed black curve represents the linear regression of experimental data (modified from Shusser et al. [8]); (b) Bubble (center circle), and thermal boundary layer (dashed, red circle) within a confining droplet (blue) under flash-boiling within another liquid medium (yellow); Rδ < Rs, (Rδ − Rb)/Rb << 1; (c) Rδ > Rs. pv,e, is the equilibrium pressure within the vapor bubble, and p∞ is the surrounding pressure (Bar-Kohany et al. Energies, 2023).
According to Mikic et al. [21] and Zanje et al. [24], flash-boiling atomization of micron-sized droplets in a highly convective environment could lead to significant bubble growth during the inertial regime [27], which can demonstrate significantly different growth rates.
Lastly, for industrial applications, more data databases are required for bubble growth in various liquids, both pure and liquid solutions, as in many of the alternative fuels that have been developed over the past few decades. Thus, current developments in flash-boiling atomization in composite droplets and micro-channels require further study of the following:
  • Bubble growth in various depressurization rates;
  • Varying pressure fields in micro-channels;
  • Validated bubble growth rates for
    ○
    Micron-sized droplets in a highly convective environment; inertial regime;
    ○
    Various liquids.

2.2. Breakup

Following the nucleation and bubble growth processes, breakup evolves, either externally or internally. Several breakup parameters have been suggested over the years as a function of non-dimensional numbers, such as Reynolds, Weber, and Ohnesorge, that describe the relations between the inertial, viscous, and surface tension forces. Excellent reviews regarding breakup mechanisms can be found in [28][29][30][31]. In the case of flash-boiling atomization, it is customary to divide the breakup regimes into three regimes, as demonstrated in Figure 4.
Figure 4.
Sauter mean diameter (SMD) vs. degree of superheat, modified from
[16]
.
 
Figure 4 illustrates the relationship between the Sauter mean diameter (SMD) and the degree of superheat. When the liquid remains subcooled, and the ambient pressure is higher than the appropriate saturation pressure (pa/psat > 1), flashing does not occur, and instead, mechanical shear and hydrodynamic instabilities can lead to a breakup and atomization of the liquid. Full shattering (flare) is achieved for high degrees of superheat (pa/psat < 0.3). Numerous correlations exist for SMD, owing to its significance and convenient use. For a comprehensive overview of SMD correlations, the reader is referred to Konstantinov et al. [32].
Witlox et al. [33] and Kitamura et al. [34] discovered additional criteria for transitioning from partial to full-shattering regimes. These criteria were found in terms of Jakob and Weber numbers. Others provided transition criteria in terms of temperature ratio (𝑇𝐿/𝑇𝑐, where Tc is the critical temperature of the fluid), and the depressurization rates. Figure 5 illustrates the required depressurization rate for the initiation of homogeneous nucleation, according to Elias Chambré [14]. As expected, the higher the temperature of the liquid prior to nucleation, the lower the depressurization rate required for the onset of homogeneous nucleation. At elevated liquid pressure and temperature values, the depressurization rate aspires to that of Hutcherson [35]. For further information, see Bar-Kohany and Levy [16].
Figure 5.
Depressurization rate vs. saturation pressure for water (modified from
[16]
).
Lamanna et al. [36] presented a unified treatment of the fully flashing disintegration regime and found that bubble nucleation and growth are the controlling mechanisms for spray atomization in the fully flashing (flare) regime.
Three breakup patterns were identified by Loureiro et al. [37]:
  • Retracing liquid. This occurs at low Webber numbers. When the surface tension forces are dominant, the liquid momentum is not sufficient to complete the breakup, and the ligaments pull the liquid back into larger droplets.
  • Ligament stretching. When thick ligaments are subjected to larger momentum forces, the ligaments are stretched until their breakup, resulting in one large droplet per interstitial volume. This is equivalent to the assumption suggested originally by Sher and Elata [38].
  • Thin lamella. When the momentum forces are large enough to overcome the viscous and surface tension forces, they lead to highly deformed bubbles. Along with the continuous evaporation of the liquid lamella, the thin liquid lamellas continue to be stretched with the growing bubbles, until they are broken into small bubbles.
Figure 6 presents the results for liquid oxygen (LOx) at 1 kPa for three different ambient temperature values (𝑇∞).
Figure 6. Breakup patterns; results shown for liquid oxygen (LOx) at 1 kPa (Loureiro et al. [37]). 𝑅*𝑓=𝑅𝑓/𝑅𝑐, 𝑅𝑓 depicts the bubble radius when it merges with another bubble, and 𝑅𝑐 depicts the critical bubble radius.
In the context of flash-boiling atomization, the following topics should be further pursued:
  • Breakup patterns for various fluids in various conditions.
  • Secondary breakup due to bubble formation within the larger droplets that continue to be superheated.
  • Spray characteristics (droplet distributions, spreading angle, penetration length, etc.) as a function of the primary and secondary breakup processes.

3. Penetration Length and Spray Collapse

Short penetration length is an important parameter in sprays, particularly in combustion chambers, since it signifies that the liquid quickly disintegrates upon being expelled from the nozzle tip, thus increasing the liquid surface area, enhancing its vaporization rate, and improving its readiness for the required mixing and combustion. Short penetration length is also important for coating and painting processes, pharmaceutical applications, and more. Compared to mechanical methods, the penetration length of a spray generated by flash-boiling is known to be shorter, for a given pressure ratio [17].
The design of multi-hole injectors has been significantly accelerated over the last decade, and the spray penetration length can no longer be considered as the individual breakup length of each plume ejected by each hole but rather as the collapse length of all plumes together until they form a single spray cloud. Recent studies have shown the significance of the plumes’ interactions, and the pressure field that is being developed between and around them. The wider cone angles, which are typical of flash-boiling atomization, should be carefully controlled in the case of multi-hole injectors. For example, Wu et al. [39] showed that wider fuel plumes induced by flash-boiling led to an increased interaction between adjacent fuel plumes and, consequently, led to early collapse. They demonstrated that the spray penetration length is significantly dependent on the number of holes, their relative positioning, and the geometry. Kapusta [40] showed that the interaction between plumes strongly depends on the number and configuration of the plumes. He argued that while a two-nozzle injector allowed air flow into the core of the spray, the six-hole injector limits the entrainment of the external air, and thus the sprays could fully collapse. Li et al. [41] examined the conditions for spray collapse and found that apart from the overlapping of plumes, vapor condensation promotes spray collapse. They found that rapid bubble bursting caused a local static pressure rise that led to vapor condensation.

4. Fluids

In addition to the traditional fuel types (e.g., gasoline, diesel, aviation fuels, and oil fuels), there are ongoing efforts to explore a wide range of alternative fuels. Flash-boiling atomization is an excellent complementary technology to be used with some of them. Alternative fuels for spark-ignition (SI) engines are usually compressed natural gas, liquified petroleum gas, and alcohol fuels (methanol, ethanol, etc.) and their various blends and surrogates. It is worth noting that ethanol has an additional benefit; it can be readily produced from biomass [42]. Di-methyl-ether (DME), biodiesel, kerosene, and a jet propellent (JP-8) are more suitable for compression-ignition engines (CI) for ground and aeronautical transportation [43]. Space applications employ cryogenic propellants such as liquid oxygen (LOx) [44], and hypergolic propellants such as hydrazine and its derivatives. Novel developments of orbital maneuvering systems are focused on alternative fuels that are both eco-friendly and safer for operation. These include conventional options such as hydrogen, methane, and kerosene [36][37]). The ultra-fine droplets that can be obtained via the flash-boiling atomization of these alternative fuels have demonstrated potential in improving engine efficiency and reducing particulate matter emission (PM) thanks to the vigorous vaporization and the faster oxidation of the soot under flash-boiling conditions [45]. It has been observed that the utilization of alternative fuels in engines can necessitate certain adjustments in terms of the most favorable operation conditions. For example, higher latent heat of vaporization of ethanol, as compared to isooctane or hexane, for example, causes severe temperature drops during flash-boiling that significantly inhibit further vaporization. This leads to a less efficient ignition under cold-start ignition and possibly larger droplet size. Moreover, a larger fraction of ethanol increases density and viscosity in the spray penetration length. However, increasing the fuel temperature to promote a full flare breakup prevails and contributes to resolving both problems.

5. Diagnostics Aspects

Droplet distribution and velocity component statistics resulting from the primary breakup play a crucial role in determining the spray quality. However, due to the dense population of droplets near the nozzle exit, it is very difficult to analyze the cloud optically [46]. Quantifying these statistics using optical diagnostic instruments is quite challenging, in particular where a flash billing spray is involved, as a faster breakup leads to a higher concentration of droplets.
Optical access to the flow inside the nozzle is imperative to a better understanding of flash-boiling atomization since it can provide essential data on the nucleation and bubbles’ growth and enable identification of flow patterns inside the nuzzle [47][48].
Several non-intrusive methods exist for diagnostics of internal and external flows during flash-boiling atomization. Most of the common diagnostic methods are optical, e.g., Shadowgraph, PIV (particle image velocimetry), various laser diagnostics, holography, etc. Consequently, much effort has been dedicated to the manufacturing of transparent nozzles [49], injectors, and cylinders [45].
Measurements along the line of sight cannot distinguish between bubble structures of overlapping bubbles in the measurement direction. The results obtained using basic planar laser-based techniques may be hindered by significant multiple scattering within the multiphase medium, which could considerably distort optical measurements.
Ultra-short pulse off-axis digital holography was used by Minniti et al. [50]. Femto-second (fs), coherence length pulses, and reference beams were used to detect ballistic photons while eliminating the signal originating from the photons that had undergone multiple scattering events. This allowed the authors to map the primary spray cone with high accuracy and to circumvent the masking via an optically dense ancillary droplet shroud.
Cavicchi et al. [51] suggested a methodology based on local momentum flux measurements. Spray impact forcefully applied to small portions of the fluid structure was used to detect the individual local contribution of the liquid and gaseous phases to the jet momentum flux. One of the primary benefits of this diagnostic methodology is the ability to examine the spray pattern in close proximity to the nozzle (down to 4–5 mm from the tip) in a wide range of atomization quality and spray drop space density.
Transparent devices require materials with a refractive index that is very close to the liquid that is being examined, and, in some cases, strength and durability under high temperatures, to allow measurements near realistic engine operating conditions. Acrylic materials, for example, have a very close refractive index (1.4–1.5, [52]) to gasoline and diesel. On the other hand, acrylic material has a relatively low melting point that prevents its use in high-temperature fuel applications such as superheated fuels. Moreover, their optical qualities are sensitive to the corrosive interaction between the acrylic material and alcohol fuels. Glass material such as fused silica has favorable optical transmission properties over a broad range of wavelengths, and its refractive index is similar to one of common fossil fuels. However, their fabrication is more challenging and bears higher manufacturing costs. Aleiferis et al. [53] conducted a refractive index matching employing a liquid flow circuit around the test section.
In addition, it is worth noting the difference in the thermal properties of the various optical materials and the materials used in real operation [54]. Thus, it is still challenging to match the performance of optical injectors with real ones. When diagnostics are employed on non-transparent devices, X-ray radiography might be a useful tool, but its limitations should be considered. It currently suffers from line-of-sight measurement drawbacks. It is, however, anticipated that X-ray techniques will become increasingly more useful and informative in the future.

References

  1. Solomon, A.S.P.; Chen, L.D.; Faeth, G.M. Investigation of Spray Characteristics for Flashing Injection of Fuels Containing Dissolved Air and Superheated Fuels; No. NAS 1.26; NASA: Washington, DC, USA, 1999; p. 3563.
  2. Skripov, V.P. Metastable Liquids; Wiley: New York, NY, USA, 1974.
  3. Carey, V.P. Liquid-Vapor Phase-Change Phenomena: An Introduction to the Thermophysics of Vaporization and Condensation Processes in Heat Transfer Equipment; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2018.
  4. Bar-Kohany, T. Minimal heating rate for isobaric nucleation at the spinodal in liquids. Int. J. Heat Mass Transf. 2021, 165, 120636.
  5. Bar-Kohany, T.; Amsalem, Y. Nucleation temperature under various heating rates. Int. J. Heat Mass Transf. 2018, 126, 411–415.
  6. Ching, E.J.; Avedisian, C.T.; Cavicchi, R.C.; Chung, D.H.; Rah, K.J.; Carrier, M.J. Rapid evaporation at the superheat limit of methanol, ethanol, butanol and n-heptane on platinum films supported by low-stress sin membranes. Int. J. Heat Mass Transf. 2016, 101, 707–718.
  7. Glod, S.; Poulikakos, D.; Zhao, Z.; Yadigaroglu, G. An investigation of microscale explosive vaporization of water on an ultrathin pt wire. Int. J. Heat Mass Transf. 2002, 45, 367–379.
  8. Shusser, M.; Weihs, D. Explosive boiling of a liquid droplet. Int. J. Multiphase. Flow. 1999, 25, 1561–1573.
  9. Skripov, P.V.; Bar-Kohany, T.; Antonov, D.V.; Strizhak, P.A.; Sazhin, S.S. Approximations for the nucleation temperature of water. Int. J. Heat Mass Transf. 2023, 207, 123970.
  10. Su, G.-Y.; Bucci, M.; McKrell, T.; Buongiorno, J. Transient boiling of water under exponentially escalating heat inputs. part i: Pool boiling. Int. J. Heat Mass Transf. 2016, 96, 667–684.
  11. Avni, O.; Bar-Kohany, T.; Sher, E. Flash-boiling atomization triggered and driven by intensive radiation. Therm. Sci. Eng. Prog. 2022, 32, 101334.
  12. Alamgir, M.; Lienhard, J.H. Correlation of Pressure Undershoot of Pressure During Hot Water Depressurization. J. Heat Trans. 1981, 103, 52–56.
  13. Barták, J. Study of the Rapid Depressurization of Hot Water and the Dynamics of Vapour Bubble Generation in Superheated Liquid. Int. J. Multiph. Flow. 1990, 16, 789–798.
  14. Elias, E.; Chambré, P.L. Flashing inception in water during rapid decompression. J. Heat Transf. 1993, 115, 231–238.
  15. Moshkovich, Y.; Levy, Y.; Sher, E. Theoretical criteria for homogeneous flash-boiling atomization. Chem. Eng. Sci. 2019, 206, 471–475.
  16. Bar-Kohany, T.; Levy, M. State of the art review of flash-boiling atomization. At. Sprays 2016, 26, 1255–1305.
  17. Sher, E.; Bar-Kohany, T.; Rashkovan, A. Flash-boiling atomization. Prog. Energy Combust Sci. 2008, 34, 417–439.
  18. Avedisian, C.T.; Skyllingstad, K.; Cavicchi, R.C.; Lippe, C.; Carrier, M.J. Initiation of flash boiling of multicomponent miscible mixtures with application to transportation fuels and their surrogates. Energy Fuels 2018, 32, 9971–9981.
  19. Sazhin, S. Droplets and Sprays; Springer: London, UK, 2014.
  20. Prosperetti, A. Vapor bubbles. Annu. Rev. Fluid. Mech. 2017, 49, 221–248.
  21. Mikic, B.B.; Rohsenow, W.M.; Griffith, P. On Bubble Growth Rates. Int. J. Heat Mass Trans. 1970, 13, 657–666.
  22. Plesset, M.; Zwick, S.A. The growth of vapor bubbles in superheated liquids. J. Appl. Phys. 1954, 25, 493–500.
  23. Mahmoud, M.M.; Karayiannis, T.G. Bubble growth on a smooth metallic surface at atmospheric and sub-atmospheric pressure. Int. J. Heat Mass Transf. 2023, 209, 124103.
  24. Zanje, S.; Iyer, K.; Murallidharan, J.S.; Punekar, H.; Gupta, V.K. Development of generalized bubble growth model for cavitation and flash boiling. Phys. Fluids 2021, 33, 077116.
  25. Jones, O.; Zuber, N. Bubble growth in variable pressure fields. J. Heat Transf. 1978, 100, 453–459.
  26. Avedisian, C.T. Bubble growth in superheated liquid droplets. Encycl. Fluid Mech. 1985, 3, 130–190.
  27. Bar-Kohany, T.; Antonov, D.V.; Strizhak, P.A.; Sazhin, S.S. Nucleation and bubble growth during puffing and micro-explosions in composite droplets. Fuel 2023, 340, 126991.
  28. Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2017.
  29. Ashgriz, N. Handbook of Atomization and Sprays: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011.
  30. Lightfoot, M. Fundamental classification of atomization processes. At. Sprays 2009, 19, 1065–1104.
  31. Schulte, K.; Tropea, C.; Weigand, B. Droplet Dynamics under Extreme Ambient Conditions; Springer Nature: Berlin/Heidelberg, Germany, 2022.
  32. Konstantinov, D.; Marsh, R.; Bowen, P.J.; Crayford, A. Effervescent Atomization for Industrial Energy–Technology Review. At. Sprays 2010, 20, 525–552.
  33. Witlox, H.; Harper, M.; Bowen, P.; Cleary, V. Flashing liquid jets and two-phase droplet dispersion: II. Comparison and validation of droplet size and rainout formulations. J. Hazard Mater. 2007, 142, 797–809.
  34. Kitamura, Y.; Morimitsu, H.; Takahashi, T. Critical superheat for flashing of superheated liquid jets. Ind. Eng. Chem. Fund. 1986, 25, 206–211.
  35. Hutcherson, M.N.; Henry, R.; Wollersheim, D. Two-phase vessel blowdown of an initially saturated liquid—Part 2: Analytical. J. Heat Transf. 1983, 105, 694–699.
  36. Lamanna, G.; Kamoun, H.; Weigand, B.; Steelant, J. Towards a unified treatment of fully flashing sprays. Int. J. Multiph. Flow. 2014, 58, 168–184.
  37. Loureiro, D.D.; Reutzsch, J.; Kronenburg, A.; Weigand, B.; Vogiatzaki, K. Primary breakup regimes for cryogenic flash atomization. Int. J. Multiph. Flow. 2020, 132, 103405.
  38. Sher, E.; Elata, C. Spray formation from pressure cans by flashing. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 237–242.
  39. Wu, S.; Yang, S.; Wooldridge, M.; Xu, M. Experimental study of the spray collapse process of multi-hole gasoline fuel injection at flash boiling conditions. Fuel 2019, 242, 109–123.
  40. Kapusta, Ł.J. Understanding the collapse of flash-boiling sprays formed by multi-hole injectors operating at low injection pressures. Energy 2022, 247, 123388.
  41. Li, Y.; Guo, H.; Fei, S.; Ma, X.; Zhang, Z.; Chen, L.; Feng, L.; Wang, Z. An exploration on collapse mechanism of multi-jet flash-boiling sprays. Appl. Therm. Eng. 2018, 134, 20–28.
  42. Fan, Y.; Sun, Z.; Gu, Q.; Xu, Q.; Li, X.; Xu, M. Combustion improved by using flash boiling sprays in an ethanol-gasoline optical engine under cold operating conditions. Energy Fuels 2021, 35, 10134–101345.
  43. Bae, C.; Kim, J. Alternative fuels for internal combustion engines. Proc. Combust. Inst. 2017, 36, 3389–3413.
  44. Lamanna, G.; Kamoun, H.; Weigand, B.; Manfletti, C.; Rees, A.; Sender, J.; Oschwald, M.; Steelant, J. Flashing behavior of rocket engine propellants. At. Sprays 2015, 25, 837–856.
  45. Sun, Z.; Yang, S.; Nour, M.; Li, X.; Hung, D.; Xu, M. Significant impact of flash boiling spray on in-cylinder soot formation and oxidation process. Energy Fuels 2020, 34, 10030–10038.
  46. Qiu, S.; Wang, S.; Zhang, Y.; Li, X.; Hung, D.; Xu, M. Dense-field spray droplet size quantification of flashing boiling atomization using structured laser illumination planar imaging technique. Fuel 2023, 335, 127085.
  47. Wang, J.; Zhou, Z.; Chen, B.; Yang, T.; Zhang, L.; Romeos, A.; Giannadakis, A.; Panidis, T. Flow visualization of the transient effect of the internal two-phase flow on the external iso-pentane flashing spray under different injection pressure. Fuel 2023, 333, 126151.
  48. Wang, S.; Qiu, S.; Zhang, Y.; Cui, M.; Li, X.; Xu, M. In-nozzle multi-phase flow patterns in flash-boiling atomization and their impacts on external sprays. Exp. Fluids 2023, 64, 48.
  49. Wu, S.; Xu, M.; Hung, D.L.; Li, T.; Pan, H. Near-nozzle spray and spray collapse characteristics of spark-ignition direct-injection fuel injectors under sub-cooled and superheated conditions. Fuel 2016, 183, 322–334.
  50. Minniti, M.; Dunn-Rankin, D.; Chien, Y.C. Long-range microscopy of optically dense spray structures using ultra-short pulse off-axis digital holography. At. Sprays 2021, 31, 47–59.
  51. Cavicchi, A.; Postrioti, L.; Sorbini, G.; Brizi, G. Local momentum flux measurement: An effective way for GDI spray targeting in flash-boiling conditions. Fuel 2022, 317, 123454.
  52. Butcher, A.J.; Aleiferis, P.G.; Richardson, D. Development of a real-size optical injector nozzle for studies of cavitation, spray formation and flash-boiling at conditions relevant to direct-injection spark-ignition engines. Int. J. Engine Res. 2013, 14, 557–577.
  53. Aleiferis, P.G.; Hardalupas, Y.; Kolokotronis, D.; Taylor, A.M.K.P.; Kimura, T. Investigation of the Internal Flow Field of a Diesel Model Injector Using Particle Image Velocimetry and cfd (No. 2007-01-1897); SAE Technical Article; SAE International: Warrendale, PA, USA, 2007.
  54. Yang, S.; Ma, Z.; Li, X.; Hung, D.L.; Xu, M. A review on the experimental non-intrusive investigation of fuel injector phase changing flow. Fuel 2020, 259, 116188.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Video Production Service
Feedback