High-Precision Quantum Tests of the Weak Equivalence Principle: Comparison
View Latest Version
Please note this is a comparison between Version 4 by Fanny Huang and Version 3 by Fanny Huang.

General relativity has been the best theory to describe gravity and space–time and has successfully explained many physical phenomena. At the same time, quantum mechanics provides the most accurate description of the microscopic world, and quantum science technology has evoked a wide range of developments today. Merging these two very successful theories to form a grand unified theory is one of the most elusive challenges in physics. All the candidate theories that wish to unify gravity and quantum mechanics predict the breaking of the weak equivalence principle, which lies at the heart of general relativity. It is therefore imperative to experimentally verify the equivalence principle in the presence of significant quantum effects of matter. Cold atoms provide well-defined properties and potentially nonlocal correlations as the test masses and will also improve the limits reached by classical tests with macroscopic bodies. The results of rigorous tests using cold atoms may tell us whether and how the equivalence principle can be reformulated into a quantum version. 

  • high-precision quantum tests
  • Weak Equivalence Principle
  • atom interferometer
  • gravity measurement

1. Introduction

Since Newton’s theory of gravity was published more than 300 years ago, and Einstein’s general relativity (GR) was further developed about 100 years ago, astonishingly good predictions and observations of the position and motion of matter have been achieved, from planets in the vast universe to objects in our everyday lives. Gravity is usually treated as a universally coupled force for all matter regardless of its properties and structure and can be considered as a geometric description of space–time in general relativity. However, it is widely accepted that the universe is expanding based on astronomical observations [1]. Currently, only 4.9% of the matter in the universe has been detected, and the existence of dark matter and dark energy has been postulated [2]. Quantum mechanics, on the other hand, governs physics at the microscopic scale, where matter has no definite trajectory and is described by wave functions. For now, properties of nonlocal entanglement and coherent correlations between microscopic particles have been rigorously demonstrated in all kinds of experiments [3][4][5][6][7]. The quantum field theory, particularly the Standard Model (SM), provides a unified description of the electromagnetic, weak, and strong interactions except gravity [8]. Despite the persistent efforts since Einstein, the unification of gravity and quantum theories remains an unresolved issue in physics. Whatever is for sure, testing gravity in the framework of quantum mechanics should lead us to a whole new understanding of the world.
The universal coupling property of gravity, known as the Einstein equivalence principle (EEP) [9], is the cornerstone of the GR [10] and other gravitational geometry theories [11]. The EEP contains three different ingredients: the weak equivalence principle (WEP), the local position invariance (LPI) and the local Lorentz invariance (LLI). The last two ingredients describe the invariance in a local non-gravitational experiment: for any local non-gravitational experiment, the experimental results are independent of the velocity and location in the spacetime of the laboratory [12] As the foundation and a key ingredient of EEP, the WEP, asserts the equivalence between the gravitational and inertial masses of a particle, and it states that all point-like neutral particles experience the same free-fall trajectories, i.e., the same gravitational accelerations, independent of the composition, mass and material of these particles [13]. Thus, the WEP is also called the universality of free fall (UFF).
Tests of the WEP hypothesis are crucial for validating Einstein’s theory or other candidate theories beyond Einstein’s theory. In fact, all the new candidate theories beyond the GR and SM, including string theory [14][15], loop quantum gravity theory [16], Standard-Model Extension [17], dilaton model [18] and the fifth force [19][20], require the WEP to be broken. Also, some novel physical phenomena, such as new interactions [21], dark matter [22] and dark energy [23], that relate to gravity can also be found/checked by verifying the WEP.
In order to verify the correctness of the above candidate theories and promote the birth of a unified theory, the traditional test of the WEP has been developed in different macroscopic domains since Galileo’s Leaning Tower experiments [24], such as the earliest single pendulum experiments (with an uncertainty of 10−610−6) [25], mass drops (uncertainty of 10−1010−10) [26][27], torsion balances (uncertainty of 10−1310−13) [28][29] and Lunar Laser Ranging (uncertainty of 10−1410−14) [30][31], to name a few. Recently, MICROSCOPE reported the highest accuracy of the WEP test at about 1.5×10−151.5×10−15 by comparing the free-fall accelerations of two masses of titanium and platinum aboard a satellite in space [32][33].
All the results strongly confirm the equivalence between inertial and gravitational masses and the great success of the GR theory, and no evidence of WEP breaking was observed. However, wresearchers are still unclear whether the WEP still holds with higher accuracy and quantum effects taken into consideration. Theoretical studies suggest that the WEP test with atoms has a potentially higher accuracy than the WEP test with macroscopic objects [34][35]. It should be of interest to test the range of applications of the WEP with microscopic particles where quantum phenomenon become significant and will help us to understand the interplay between gravity and quantum physics. Due to the abundant degrees of freedom among the microscopic particles, it is also worth performing WEP verification experiments utilizing atoms with different properties, such as the proton and neutron number, the internal quantum states or spin and the nonlocal correlations that may lead to the coupling interaction between gravity and other forces. Meanwhile, some theories suggest that microscopic particles will exhibit different behaviors compared to macroscopic objects that would violate the WEP. For example, macroscopic objects are insensitive to the chameleon field due to the shielding mechanism; nevertheless, the atoms in vacuum can interact with the field [36][37][38][39][40]. Similar examples showing such distinction between atoms and macroscopic objects could be the case when the atoms have the controllable spin degree of freedom, and the spin-torsion coupling in gravity field, which is absent in the macroscopic objects, would break the WEP [41][42][43][44][45][46]. These studies will provide directions or clues to explore new mechanisms and interactions that may lead to the WEP breaking.
2. Key Techniques and Systematic Effects

2. Key Techniques and Systematic Effects

Current accuracy of the Eötvös parameter 𝜂  is at the level of 10−1110−11 for different internal states of the same species and 10−1210−12 for different isotopes but only 10−710−7 for different atom species. This is far away from the accuracy of 10−1510−15 using the macroscopic classical masses [32]. Thus, to achieve the high precision in the WEP test with atom interferometers, one main challenge that researchers should put in the first priority is to obtain higher sensitivity, accuracy and stability of gravity measurement. Currently, the sensitivity of gravity measurement using atom interferometers is at the level of 10−9 g/Hz−−−√Hz Hz , which is the key obstacle that limits accuracy improvements.
In addition, the atoms used for the WEP tests are mainly the alkali metals, especially the rubidium atoms. High-rate cooling and trapping of other atomic species is demanding for a richer variety of the WEP tests. Also, researchers do not explore all factors for carrying out the WEP tests but focus on some key techniques and systematic effects, such as preparation and control of laser pulse, atom trajectory and interference signal detection, gravity gradient, wavefront aberration and suppression of vibration noise and other major noises. Actually, what researchers focus on is the differential phase of the two components in the WEP test experiment with dual species. Through certain methods, most of the noise can be suppressed as common-mode noise.
 

2.1. Preparation and Control of Laser Pulse

In a Raman-type atom interferometer, the Raman light is the core technology to split and reflect atoms, with which the hyperfine ground states of atoms are coupled through the two-photon resonance. In order to realize the two-photon resonance during the atom dropping, researchers need to tune the frequency of the Raman light to compensate the Doppler frequency drift. In the meanwhile, to realize stable and significant atom interference pattern, the active feedback technique is also necessary to eliminate the phase fluctuations and noises in the Raman pulses.
There are several methods to realize Raman light, including optical phase-locked loop (OPLL) [47][48], acousto-optic modulation (AOM) [49][50] and electro-optic modulation (EOM) [51][52]. The OPLL is used between two independent lasers, whose system is complex and not conducive for miniaturization and integration. It has low noise in the low frequency range (10–100 Hz), but due to the influence of the feedback circuit, the phase noise in the high frequency range is extremely high [53]. The AOM scheme has significant low phase noise. However, the frequency shift of the AOM is generally lower than 5 GHz, and the diffraction efficiency is extremely low for the high frequency that requires large laser power. Wang et al. combined the OPLL and AOM schemes to achieve low phase noise with broad bands [54]. The general EOM scheme is compact and simple but will generate double sidebands, causing unwanted power waste and system errors [55][56].
Based on the electro-optic effect, a cascaded Mach–Zehnder interferometer is used to apply orthogonal phase modulation to the optical signal, which can achieve a method called optical single-sideband modulation. This technology tunes the ratio–frequency phase shifter and bias voltages on an in-phase/quadrature (I/Q) modulator and has achieved the reduction of errors caused by unnecessary sidebands [57][58]. The I/Q modulator is essentially a cascaded Mach–Zehnder interferometer, as shown in Figure 1. The main noise using single-sideband lasers comes from the fluctuations in the sideband/carrier ratio, which leads to the extra phase shift in gravity measurement [58]. In 2019, a portable atom gravimeter based on this simple optical protocol was implemented [59].
Figure 1. Internal diagram of an I/Q modulator. 𝐸in and 𝐸out: the input and output laser field; 𝛿𝜙𝑆=𝛽sin𝜔𝑚𝑡 and 𝛿𝜙𝐶=𝛽cos𝜔𝑚𝑡: the sine and cosine phase modulator; Φ1,2,3: optical phase shifter; MZM: Mach–Zehnder modulation.
Alternative methods. including Bragg diffraction [60][61][62] and Bloch oscillation [63][64][65], can also be used as beam splitters and mirrors to achieve the atom wave packet splitting and reflection. Different from the Raman pulse, the laser used in Bragg diffraction does not need high frequency modulation since it is a process of photon recoil momentum transfer in the same internal state. Thus, the Bragg method provides well rejection of the external field influence. Bloch oscillation, which forms a moving optical lattice by two counter-propagating laser beams with small frequency difference 𝛿𝜈, can accelerate the atoms and achieve a large momentum transfer (LMT) beam splitter. Furthermore, researchers can improve sensitivity and accuracy of the atom interferometers by employing a sequence of light pulses, which combines the advantages of the techniques of Raman transition, Bragg diffraction and Bloch oscillation [66]. In addition to the ordinary two-photon or multi-photon transition schemes, there is also another scheme of atom interferometer based on the single-photon ultranarrow clock transition of strontium atoms, which greatly reduces susceptibility to the laser noise [67]. In addition, the cavity-enhanced light–atom interaction can provide advantage of power enhancement and spatial filtering and pave the way toward large-scale and high-sensitivity interferometer [68][69].

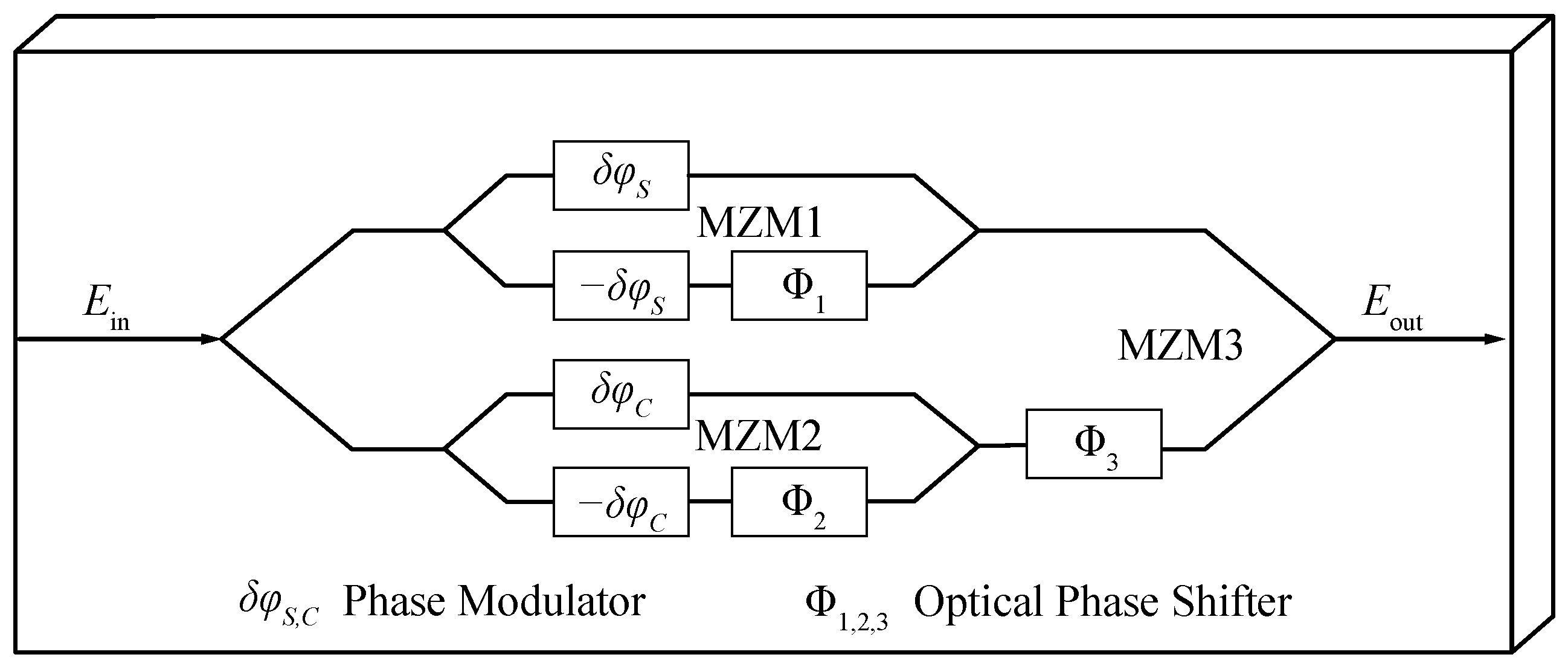
2.2. Atom Trajectory and Signal Detection

In the experiments, the phase that contains gravity information can be retrieved by detecting the population of atoms as per Equations (4) and (5). To minimize the errors in measuring the atoms’ population, researchers need to trace the atom’s trajectory and develop techniques to analyze the detection signals. 
There are two main concerns in atom trajectory. One is that the mismatch between the atom trajectory and Raman pulse sequence can lower the interference fringe contrast and increase the amplitude noise, which is the noise shown in 𝑃amp in Equation (4). The effect of such mismatch is significant in experiments with large interference loop areas. The other one is the mismatch of atom trajectories of different components in the dual-species atom interferometer. When researchers extract the differential phase, the asynchronous drift of atoms of different species can reduce the level of common-mode noise suppression. Therefore, the symmetry and overlap of atom trajectories is crucial in the performance of dual-species atom interferometers. To trace the atom trajectory, Yao et al. proposed an experiment setup to include two sets of Raman lights in the atom interferometers, of which one set is along the moving direction of atoms to monitor the position of atoms, and the other set is vertical to the moving direction of atoms to measure the velocity of atoms [70]. In 2022, their setup was upgraded to introduce the active feedback control in the calibration of the atom trajectories, of which the stability was improved by two orders of magnitude [71].
In the detection, the experimental data are the fluorescence signals from the spontaneous radiation of the pumped-up atoms. The intensity of the signals gives us the atom population, which could be fluctuating due to the imbalance of intensities of the trapping lasers and the drift of the magnetic field. Such fluctuation in the total atom number, which is one cause of the amplitude noise, can be suppressed by a normalization detection method, such as the two-state sequential detection [72] and two-state simultaneous detection [73]. To further simplify the normalized detection process, Song et al. proposed to normalize the atomic population by the quenched fluorescence signals during initial state preparation [74].
In processing the data, different techniques have been developed to extract the differential phase signal ΔΦ𝐴−ΔΦ𝐵 in the dual-atom interferometer. In the case when the common-mode noise is comparable to the differential phase signal, where the least squares method may fail to fit the data, the method of ellipse fitting [75] can be used to extract the differential phase. However, the ellipse fitting method would introduce significant bias and may not provide the optimal fit with the prior knowledge of the noise. The problem was overcome by incorporating the ellipse fitting with the Bayesian estimation by Stockton et al. [76], which was applied to extract the differential acceleration with atoms of different masses in the proposal of Varoquaux et al. in 2009 [77]. Such a Bayesian estimation method was later developed by Chen et al. [78] and Barrett et al. [79]. Barrett et al. also applied a Bayesian estimation method in the WEP test experiments with K and Rb atoms [79]. In 2016, Wang et al. proposed to combine the linear and ellipse fitting methods to extract the differential phase [80]. This method can accurately extract the small differential phase in the noisy environment, which makes up for the shortcomings of the ellipse fitting method and the Bayesian statistics statistical method. There are also other techniques in data processing for some particular application scenarios, such as the spectrum correlation method for the WEP test using atoms in a spacecraft [81].

2.3. Major Systematic Effects

2.3.1. Gravity Gradient and Coriolis Effect

The gravity gradient is one of the most serious systematic effects in the WEP test. Due to the Earth’s gravitational field and mass distribution surrounding the atoms, The gravity acceleration is usually not constant along the trajectories of the atoms. gravity gradient can give rise to an additional phase shift as it couples to the initial velocity and position of the atoms [82]. For a cold atomic ensemble with an initial statistical distribution, there is an unavoidable phase uncertainty, especially for the long-baseline interferometer. In addition, there exist higher-order systematic errors in the WEP test when different atoms move in different trajectories.
Roura proposed a scheme to overcome the influences of the gravity gradient and meet the requirements of the initial colocalization of two atom ensembles A and B by changing the effective momentum transfer in the Raman transition using the 𝜋-pulse at 𝑡=𝑇 [83]. Shortly after, D’Amico et al. experimentally demonstrated this method and showed its promising high sensitivity and accuracy even in the presence of nonuniform forces [84]. Overstreet et al. created an effective inertial frame that could suppress the error of the gravity gradient to 10−13 g10−13 g  by selecting the appropriate frequency shift of Raman pulse [85]. In the spaceborne test of the WEP, Chiow et al. showed that the gravity inversion and modulation using a gimbal mount can suppress gravity gradient errors, which reduces the need to overlap two species of atoms [86].
Similar to the gravity gradient, the Coriolis effect, which is caused by the Earth’s rotation, leads to one systematic error manifested as the deviation of the atoms’ trajectories when the atoms initially possess the transverse velocity with respect to the incident laser beams [87]. Duan et al. presented detailed discussions on how to suppress the Coriolis error in the WEP test using a dual-species atom interferometer [88]. They reduced the uncertainty of the 𝜂 introduced by the Coriolis force to 10−1110−11  by rotating the Raman laser reflector. Lan et al. used a tip–tilt mirror to compensate the phase shift caused by the Coriolis force and improved the contrast of interference fringes [89]. Louchet-Chauvet et al. measured gravity values in the direction opposite to the Earth’s rotation vector, separated the influence and corrected the Coriolis shift [90].

2.3.2. Wavefront Aberrations

Waveform aberrations, as one main factor that leads to the systematic uncertainty [91][92], are caused by the imperfections of the laser beam profiles and the retro-reflecting mirrors in the atom interferometers. Without any optimization, the uncertainty contribution of this factor in gravity measurement is on the level of 10−9 g, which strongly limits the accuracy of the WEP test. Wang et al. analyzed the influence of the wavefront curvature of Raman pulses by the method of a transmission matrix [93]. Schkolnik et al. presented a experimental analysis of wavefront curvature based on measured aberrations of optical windows. The uncertainty of the measured gravity is less than 3 × 10−10 g [91]. Zhou et al. presented a detailed theoretical analysis of wavefront aberrations and measured the effect by modulating the waist of Raman beams [94]. Trimeche et al. used deformable mirrors to actively control the laser wavefront and achieve compensation for wavefront curvature [95]. Hu et al. proposed an expansion-rate-selection method to suppress the aberration phase noise in the WEP test using dual-species atom interferometers [92]. The simulations showed that the suppressed uncertainty to the Eötvös parameter is on the level of 10−14 for isotopic atoms and 10−13 for nonisotopic atoms. Better results can be obtained by using atoms with lower temperature. Karcher et al. established a thorough model to study the influence of wavefront curvature on atom interferometer and proposed a method to correct for this bias based on the extrapolation of the measurements down to zero temperature [96].

2.3.3. Stark and Zeeman Effects

The Stark effect resulting from the laser beams is an important systematic error. Particularly for the WEP test with two atomic species, researchers need to use two lasers with different wavelengths, where the crosstalk between these two lasers may influence the results. One possible solution is to choose lasers with zero-magic or tune-out wavelengths to selectively manipulate the two atomic species [97].
The Zeeman effect caused by the inhomogeneous magnetic field can also lead to the error in the atom interferometer. For the magnetically insensitive states of atoms, i.e., the atomic states with 𝑚𝐹=0, though the first-order term of the Zeeman effect is zero, the nontrivial higher-order terms still exist due to the nonzero gradient of the magnetic field and contribute as one main error in the measurement of 𝜂 when two bodies of atoms A and B experience the Zeeman effect differently. Such an error is especially significant for interference using two kinds of atoms. For example, the second-order term of the Zeeman effect in the K atom is 15 times that in the Rb atom.
An accurate evaluation of the second-order Zeeman effect can greatly improve the WEP verification accuracy. Hu et al. reported an experimental investigation of the Raman-spectroscopy-based magnetic field measurements. The second-order Zeeman effect in the atom interferometer is evaluated with this method, and the uncertainty is 2.04×10−9 g [98]. In addition to providing a stable magnetic field, establishing a magnetic shield in the region of the atom interference is also an irreplaceable method. Wodey et al. designed a modular and scalable magnetic shielding device for ultra long-baseline atom interferometer measurement systems, limiting the magnetic-field-related errors in atom interferometer to the 10−13 g level [99]. Ji et al. achieved a high-performance magnetic shielding system for a long-baseline atom interferometer by combining passive shielding of permalloy with active compensation of coils. The system is expected to reduce the error of quadratic Zeeman effect to the 10−13 level in the WEP test [100]. Hobson et al. solved the magnetic field distortion caused by magnetic shielding by designing multiple coils on the coil support to generate three uniform and three constant gradient fields [101].

2.3.4. Atoms Interaction and Self-Attraction Effect

To obtain high precise measurement of the gravity difference, atoms prepared in a Bose–Einstein condensate (BEC) would be an ideal candidate, but the phase shifts and errors introduced by the atomic interactions in BEC must be accurately calculated or estimated [102][103][104][105]. Jannin et al. proposed a theoretical model based on a perturbative approach for the precise calculation of the phase shift introduced by atom–atom interactions [102]. Yao et al. used the Feynman path integral method to evaluate the phase shift of atomic interactions, and the method is in good agreement with experimental results [104]. Burchianti et al. proposes that atom–atom interactions only introduce local phase shifts in the region where wave packets overlap [105].
The self-attraction effect caused by the gravitational force generated by the surrounding mass experimental devices is also one of the errors that needs to be evaluated [106][107]. Based on the finite element method, D’Agostino et al. presented a numerical method for the calculation of the self-gravity effect in atom interferometers [107]. The numerical uncertainty introduced by this effect is 10−9 g in the measurement of gravity.

2.4. Noise Suppression

Environmental vibration noise is one of the critical issues that needs to be overcome in the realization of high-precision atom interferometer. Ground and equipment vibrations, especially in the low frequency range between 0.01 Hz and 10 Hz, are transmitted to the reflector of the Raman beam, which influences the interference fringes. Thus, performing the WEP tests on the ground preferably requires a very quiet environment and passive and/or active vibration reduction.
Early in 1999, Steve Chu’s group applied ultra-low-frequency active damping technology to reduce the vibration error of frequency from 0.1 Hz to 20 Hz by a factor of 300 [108]. The group from WIPM built the active vibration reduction system on one passive vibration reduction platform and suppressed the vertical vibration noise by 300 times from frequency of 0.1–10 Hz [109]. The HUST group developed a three-dimensional active vibration reduction system and solved the coupling problem between the horizontal and vertical vibrations [110]. This isolator is especially suitable for atom interferometers whose sensitivity is limited by the vibration noise. Common-mode vibration noise can be suppressed by 94 dB for a simultaneous dual-species atom interferometer [111]. Chen et al. proposed a proportional-scanning-phase method to reduce the vibration noise and pointed out that the ratio of the induced phases by vibration noise is constant between two atom interferometers at every experimental data point [78].
As mentioned above, the noises of the Raman pulses (power, frequency, and phase), the asymmetric atom trajectories, the influence of gravity gradient, etc., can limit the precision of the measurement. One method is to eliminate them as common-mode noises for the two test bodies. Obviously, the atom interferometers using the same laser light on the two atom ensembles can reject most of the noises up to a large scaling factor. For atom interferometer experiments, Lévèque et al. adopted a double-diffraction Raman transition technique, as shown in Figure 2a [112][113]. It requires three Raman beams, two of which are the chirped beams blue and red detuned to the upper energy level. The scanning directions of the two light beams are opposite, and the interference path is completely symmetrical, which can reduce the error caused by the gravity gradient. Since the atoms in the different trajectories are in the same energy level, it is also insensitive to the magnetic field and AC Stark effect. In 2015, Zhou et al. applied this technology to a dual-species atom interferometer and implemented a four-wave double-diffraction Raman transition (FWDR) method for the WEP test [114]. The principle of the FWDR atom interferometer is shown in Figure 2b, which requires four Raman beams (𝑘1,𝑘2,𝑘3,𝑘4) to achieve the synchronous differential measurement of the dual-species atom interference. 𝑘1 and 𝑘2 together with 𝑘3 interaction with 85Rb85Rb, while 𝑘1 and 𝑘2 together with 𝑘4 interaction with 87Rb87Rb. This scheme will greatly reduce influence from the laser phase noise and Stark and Zeeman shifts. To suppress the vibration noise of the platform, Bayesian statistical methods are introduced to extract the acceleration difference in a common-mode noise immune way by taking advantage of phase-correlated measurements [76][77]. For the dual-species WEP test, the Hu group applied the fringe-locking method, which fixes the phase measurement invariably at the midfringe [115]. This method extracts the gravity differential phase without bias and effectively suppresses common-mode vibration noise.
Symmetry 15 01769 g004
Figure 2. Schematic of double-diffraction Raman transition (a) and four-wave double-diffraction Raman transition (b). 𝑘1, 𝑘2, 𝑘3 and 𝑘4 are wave vectors of the Raman beams, T is the free evolution time, and 2𝑆 is the enclosed area of the interference.

2.5. Integrated Packages

Although atom interferometers are typically implemented in ground laboratories, current efforts aim to develop various system packages that are compatible with system integration and modularity for space missions [116][117] and with the size, weight, power consumption and robustness required for the commercial scenarios. Examples are the portable magneto-optical trap system [118], titanium vacuum package [119], laser system package [120] and cold atom physics package [121]. researchers are not discussing the details here.

References

  1. Kragh, H.; Smith, R.W. Who discovered the expanding universe? Hist. Sci. 2003, 41, 141–162.
  2. Ade, P.A.; Aghanim, N.; Alves, M.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Aussel, H.; Baccigalupi, C.; et al. Planck 2013 results. I. Overview of products and scientific results. Astron. Astrophys. 2014, 571, A1.
  3. Bell, J.S. On the Problem of Hidden Variables in Quantum Mechanics. Rev. Mod. Phys. 1966, 38, 447–452.
  4. Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195–200.
  5. Aspect, A.; Dalibard, J.; Roger, G. Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807.
  6. Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576.
  7. Mintert, F.; Kuś, M.; Buchleitner, A. Concurrence of Mixed Multipartite Quantum States. Phys. Rev. Lett. 2005, 95, 260502.
  8. Yang, C.N.; Mills, R.L. Conservation of Isotopic Spin and Isotopic Gauge Invariance. Phys. Rev. 1954, 96, 191–195.
  9. Dicke, R. Republication of: The theoretical significance of experimental relativity. Gen. Relativ. Gravit. 2019, 51, 1–31.
  10. Whitrow, G.J. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. Phys. Bull. 1974, 25, 65.
  11. Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935.
  12. Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University: Cambridge, UK, 2018.
  13. Ciufolini, I.; Wheeler, J.A. Gravitation and Inertia; Princeton University Press: Princeton, NJ, USA, 1995; Volume 101.
  14. Damour, T.; Polyakov, A.M. String theory and gravity. Gen. Relativ. Gravit. 1994, 26, 1171–1176.
  15. Scherk, J.; Schwarz, J. Dual models and the geometry of space-time. Phys. Lett. B 1974, 52, 347–350.
  16. Chiou, D.W. Loop quantum gravity. Int. J. Mod. Phys. D 2015, 24, 1530005.
  17. Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009.
  18. Damour, T. Theoretical aspects of the equivalence principle. Class. Quantum Gravity 2012, 29, 184001.
  19. Fayet, P. A new long-range force? Phys. Lett. B 1986, 171, 261–266.
  20. Fayet, P. The fifth interaction in grand-unified theories: A new force acting mostly on neutrons and particle spins. Phys. Lett. B 1986, 172, 363–368.
  21. Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A. General relativistic effects in atom interferometry. Phys. Rev. D 2008, 78, 042003.
  22. Graham, P.W.; Kaplan, D.E.; Mardon, J.; Rajendran, S.; Terrano, W.A. Dark matter direct detection with accelerometers. Phys. Rev. D 2016, 93, 075029.
  23. Hees, A.; Minazzoli, O.; Savalle, E.; Stadnik, Y.V.; Wolf, P. Violation of the equivalence principle from light scalar dark matter. Phys. Rev. D 2018, 98, 064051.
  24. Sondag, A.; Dittus, H. Electrostatic Positioning System for a free fall test at drop tower Bremen and an overview of tests for the Weak Equivalence Principle in past, present and future. Adv. Space Res. 2016, 58, 644–677.
  25. Potter, H.H.; Richardson, O.W. Some experiments on the proportionality of mass and weight. Proc. R. Soc. Lond. Ser. A 1923, 104, 588–610.
  26. Carusotto, S.; Cavasinni, V.; Mordacci, A.; Perrone, F.; Polacco, E.; Iacopini, E.; Stefanini, G. Test of g universality with a Galileo type experiment. Phys. Rev. Lett. 1992, 69, 1722–1725.
  27. Carusotto, S.; Cavasinni, V.; Perrone, F.; Polacco, E.; Iacopini, E.; Stefanini, G. g-Universality test with a Galileo’s type experiment. Nuov. Cim. B 1996, 111, 1259–1275.
  28. Schlamminger, S.; Choi, K.Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the Equivalence Principle Using a Rotating Torsion Balance. Phys. Rev. Lett. 2008, 100, 041101.
  29. Zhu, L.; Liu, Q.; Zhao, H.H.; Gong, Q.L.; Yang, S.Q.; Luo, P.; Shao, C.G.; Wang, Q.L.; Tu, L.C.; Luo, J. Test of the Equivalence Principle with Chiral Masses Using a Rotating Torsion Pendulum. Phys. Rev. Lett. 2018, 121, 261101.
  30. Viswanathan, V.; Fienga, A.; Minazzoli, O.; Bernus, L.; Laskar, J.; Gastineau, M. The new lunar ephemeris INPOP17a and its application to fundamental physics. Mon. Not. R. Astron. Soc. 2018, 476, 1877–1888.
  31. Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quantum Gravity 2018, 35, 035015.
  32. Touboul, P.; Métris, G.; Rodrigues, M.; Bergé, J.; Robert, A.; Baghi, Q.; André, Y.; Bedouet, J.; Boulanger, D.; Bremer, S.; et al. MICROSCOPE Mission: Final Results of the Test of the Equivalence Principle. Phys. Rev. Lett. 2022, 129, 121102.
  33. Touboul, P.; Métris, G.; Rodrigues, M.; Bergé, J.; Robert, A.; Baghi, Q.; André, Y.; Bedouet, J.; Boulanger, D.; Bremer, S.; et al. Result of the MICROSCOPE weak equivalence principle test. Class. Quantum Gravity 2022, 39, 204009.
  34. Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A. Testing General Relativity with Atom Interferometry. Phys. Rev. Lett. 2007, 98, 111102.
  35. Miffre, A.; Jacquey, M.; Büchner, M.; Trénec, G.; Vigué, J. Atom interferometry. Phys. Scr. 2006, 74, C15.
  36. Khoury, J. Chameleon field theories. Class. Quantum Gravity 2013, 30, 214004.
  37. Burrage, C.; Copeland, E.J.; Hinds, E. Probing dark energy with atom interferometry. J. Cosmol. Astropart. Phys. 2015, 2015, 042.
  38. Hamilton, P.; Jaffe, M.; Haslinger, P.; Simmons, Q.; Müller, H.; Khoury, J. Atom-interferometry constraints on dark energy. Science 2015, 349, 849–851.
  39. Burrage, C.; Copeland, E.J. Using atom interferometry to detect dark energy. Contemp. Phys. 2016, 57, 164–176.
  40. Elder, B.; Khoury, J.; Haslinger, P.; Jaffe, M.; Müller, H.; Hamilton, P. Chameleon dark energy and atom interferometry. Phys. Rev. D 2016, 94, 044051.
  41. Puetzfeld, D.; Obukhov, Y.N. Propagation equations for deformable test bodies with microstructure in extended theories of gravity. Phys. Rev. D 2007, 76, 084025.
  42. Yasskin, P.B.; Stoeger, W.R. Propagation equations for test bodies with spin and rotation in theories of gravity with torsion. Phys. Rev. D 1980, 21, 2081–2094.
  43. Hehl, F.W.; von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416.
  44. Shapiro, I. Physical aspects of the space–time torsion. Phys. Rep. 2002, 357, 113–213.
  45. Obukhov, Y.N.; Silenko, A.J.; Teryaev, O.V. Spin-torsion coupling and gravitational moments of Dirac fermions: Theory and experimental bounds. Phys. Rev. D 2014, 90, 124068.
  46. Hammond, R.T. Torsion gravity. Rep. Prog. Phys. 2002, 65, 599.
  47. Cacciapuoti, L.; de Angelis, M.; Fattori, M.; Lamporesi, G.; Petelski, T.; Prevedelli, M.; Stuhler, J.; Tino, G.M. Analog+digital phase and frequency detector for phase locking of diode lasers. Rev. Sci. Instrum. 2005, 76, 053111.
  48. Tackmann, G.; Gilowski, M.; Schubert, C.; Berg, P.; Wendrich, T.; Ertmer, W.; Rasel, E.M. Phase-locking of two self-seeded tapered amplifier lasers. Opt. Express 2010, 18, 9258–9265.
  49. Lenef, A.; Hammond, T.D.; Smith, E.T.; Chapman, M.S.; Rubenstein, R.A.; Pritchard, D.E. Rotation Sensing with an Atom Interferometer. Phys. Rev. Lett. 1997, 78, 760–763.
  50. Müller, H.; Chiow, S.W.; Long, Q.; Herrmann, S.; Chu, S. Atom Interferometry with up to 24-Photon-Momentum-Transfer Beam Splitters. Phys. Rev. Lett. 2008, 100, 180405.
  51. Weitz, M.; Young, B.C.; Chu, S. Atomic Interferometer Based on Adiabatic Population Transfer. Phys. Rev. Lett. 1994, 73, 2563–2566.
  52. Shahriar, M.; Turukhin, A.; Liptay, T.; Tan, Y.; Hemmer, P. Demonstration of injection locking a diode laser using a filtered electro-optic modulator sideband. Opt. Commun. 2000, 184, 457–462.
  53. Yim, S.H.; Lee, S.B.; Kwon, T.Y.; Park, S.E. Optical phase locking of two extended-cavity diode lasers with ultra-low phase noise for atom interferometry. Appl. Phys. B 2014, 115, 491–495.
  54. Wang, K.; Yao, Z.; Li, R.; Lu, S.; Chen, X.; Wang, J.; Zhan, M. Hybrid wide-band, low-phase-noise scheme for Raman lasers in atom interferometry by integrating an acousto-optic modulator and a feedback loop. Appl. Opt. 2016, 55, 989–992.
  55. Weitz, M.; Young, B.C.; Chu, S. Atom manipulation based on delayed laser pulses in three- and four-level systems: Light shifts and transfer efficiencies. Phys. Rev. A 1994, 50, 2438–2444.
  56. Li, R.B.; Zhou, L.; Wang, J.; Zhan, M.S. Measurement of the quadratic Zeeman shift of 85Rb hyperfine sublevels using stimulated Raman transitions. Opt. Commun. 2009, 282, 1340–1344.
  57. Zhu, L.; Lien, Y.H.; Hinton, A.; Niggebaum, A.; Rammeloo, C.; Bongs, K.; Holynski, M. Application of optical single-sideband laser in Raman atom interferometry. Opt. Express 2018, 26, 6542–6553.
  58. Rammeloo, C.; Zhu, L.; Lien, Y.H.; Bongs, K.; Holynski, M. Performance of an optical single-sideband laser system for atom interferometry. J. Opt. Soc. Am. B 2020, 37, 1485–1493.
  59. Luo, Q.; Zhang, H.; Zhang, K.; Duan, X.C.; Hu, Z.K.; Chen, L.L.; Zhou, M.K. A compact laser system for a portable atom interferometry gravimeter. Rev. Sci. Instrum. 2019, 90, 043104.
  60. Giltner, D.M.; McGowan, R.W.; Lee, S.A. Atom Interferometer Based on Bragg Scattering from Standing Light Waves. Phys. Rev. Lett. 1995, 75, 2638–2641.
  61. Siemß, J.N.; Fitzek, F.; Abend, S.; Rasel, E.M.; Gaaloul, N.; Hammerer, K. Analytic theory for Bragg atom interferometry based on the adiabatic theorem. Phys. Rev. A 2020, 102, 033709.
  62. Béguin, A.; Rodzinka, T.; Vigué, J.; Allard, B.; Gauguet, A. Characterization of an atom interferometer in the quasi-Bragg regime. Phys. Rev. A 2022, 105, 033302.
  63. Cladé, P.; Guellati-Khélifa, S.; Nez, F.; Biraben, F. Large Momentum Beam Splitter Using Bloch Oscillations. Phys. Rev. Lett. 2009, 102, 240402.
  64. Müller, H.; Chiow, S.; Herrmann, S.; Chu, S. Atom Interferometers with Scalable Enclosed Area. Phys. Rev. Lett. 2009, 102, 240403.
  65. McAlpine, K.E.; Gochnauer, D.; Gupta, S. Excited-band Bloch oscillations for precision atom interferometry. Phys. Rev. A 2020, 101, 023614.
  66. McGuirk, J.M.; Snadden, M.J.; Kasevich, M.A. Large Area Light-Pulse Atom Interferometry. Phys. Rev. Lett. 2000, 85, 4498–4501.
  67. Hu, L.; Poli, N.; Salvi, L.; Tino, G.M. Atom Interferometry with the Sr Optical Clock Transition. Phys. Rev. Lett. 2017, 119, 263601.
  68. Hamilton, P.; Jaffe, M.; Brown, J.M.; Maisenbacher, L.; Estey, B.; Müller, H. Atom Interferometry in an Optical Cavity. Phys. Rev. Lett. 2015, 114, 100405.
  69. Nourshargh, R.; Lellouch, S.; Hedges, S.; Langlois, M.; Bongs, K.; Holynski, M. Circulating pulse cavity enhancement as a method for extreme momentum transfer atom interferometry. Commun. Phys. 2021, 4, 257.
  70. Yao, Z.W.; Lu, S.B.; Li, R.B.; Luo, J.; Wang, J.; Zhan, M.S. Calibration of atomic trajectories in a large-area dual-atom-interferometer gyroscope. Phys. Rev. A 2018, 97, 013620.
  71. Zhu, L.; Zhong, J.; Zhang, X.; Lyu, W.; Liu, W.; Xu, W.; Chen, X.; Wang, J.; Zhan, M. Feedback control of atom trajectories in a horizontal atom gravity gradiometer. Opt. Express 2022, 30, 10071–10083.
  72. Rocco, E.; Palmer, R.N.; Valenzuela, T.; Boyer, V.; Freise, A.; Bongs, K. Fluorescence detection at the atom shot noise limit for atom interferometry. New J. Phys. 2014, 16, 093046.
  73. Biedermann, G.W.; Wu, X.; Deslauriers, L.; Takase, K.; Kasevich, M.A. Low-noise simultaneous fluorescence detection of two atomic states. Opt. Lett. 2009, 34, 347–349.
  74. Song, H.; Zhong, J.; Chen, X.; Zhu, L.; Wang, Y.; Wang, J.; Zhan, M. Normalized detection by using the blow-away signal in cold atom interferometry. Opt. Express 2016, 24, 28392–28399.
  75. Foster, G.T.; Fixler, J.B.; McGuirk, J.M.; Kasevich, M.A. Method of phase extraction between coupled atom interferometers using ellipse-specific fitting. Opt. Lett. 2002, 27, 951–953.
  76. Stockton, J.K.; Wu, X.; Kasevich, M.A. Bayesian estimation of differential interferometer phase. Phys. Rev. A 2007, 76, 033613.
  77. Varoquaux, G.; Nyman, R.A.; Geiger, R.; Cheinet, P.; Landragin, A.; Bouyer, P. How to estimate the differential acceleration in a two-species atom interferometer to test the equivalence principle. New J. Phys. 2009, 11, 113010.
  78. Chen, X.; Zhong, J.; Song, H.; Zhu, L.; Wang, J.; Zhan, M. Proportional-scanning-phase method to suppress the vibrational noise in nonisotope dual-atom-interferometer-based weak-equivalence-principle-test experiments. Phys. Rev. A 2014, 90, 023609.
  79. Barrett, B.; Antoni-Micollier, L.; Chichet, L.; Battelier, B.; Gominet, P.A.; Bertoldi, A.; Bouyer, P.; Landragin, A. Correlative methods for dual-species quantum tests of the weak equivalence principle. New J. Phys. 2015, 17, 085010.
  80. Wang, Y.P.; Zhong, J.Q.; Chen, X.; Li, R.B.; Li, D.W.; Zhu, L.; Song, H.W.; Wang, J.; Zhan, M.S. Extracting the differential phase in dual atom interferometers by modulating magnetic fields. Opt. Commun. 2016, 375, 34–37.
  81. Hu, J.G.; Chen, X.; Wang, L.Y.; Liao, Q.H.; Wang, Q.N. Systematic error suppression scheme of the weak equivalence principle test by dual atom interferometers in space based on spectral correlation. Chin. Phys. B 2020, 29, 110305.
  82. Antoine, C.; Bordé, C.J. Quantum theory of atomic clocks and gravito-inertial sensors: An update. J. Opt. B Quantum Semiclass. Opt. 2003, 5, S199.
  83. Roura, A. Circumventing Heisenberg’s Uncertainty Principle in Atom Interferometry Tests of the Equivalence Principle. Phys. Rev. Lett. 2017, 118, 160401.
  84. D’Amico, G.; Rosi, G.; Zhan, S.; Cacciapuoti, L.; Fattori, M.; Tino, G.M. Canceling the Gravity Gradient Phase Shift in Atom Interferometry. Phys. Rev. Lett. 2017, 119, 253201.
  85. Overstreet, C.; Asenbaum, P.; Kovachy, T.; Notermans, R.; Hogan, J.M.; Kasevich, M.A. Effective Inertial Frame in an Atom Interferometric Test of the Equivalence Principle. Phys. Rev. Lett. 2018, 120, 183604.
  86. Chiow, S.; Williams, J.; Yu, N.; Müller, H. Gravity-gradient suppression in spaceborne atomic tests of the equivalence principle. Phys. Rev. A 2017, 95, 021603.
  87. Peters, A.; Chung, K.Y.; Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 2001, 38, 25–61.
  88. Duan, W.T.; He, C.; Yan, S.T.; Ji, Y.H.; Zhou, L.; Chen, X.; Wang, J.; Zhan, M.S. Suppression of Coriolis error in weak equivalence principle test using 85Rb–87Rb dual-species atom interferometer. Chin. Phys. B 2020, 29, 070305.
  89. Lan, S.Y.; Kuan, P.C.; Estey, B.; Haslinger, P.; Müller, H. Influence of the Coriolis Force in Atom Interferometry. Phys. Rev. Lett. 2012, 108, 090402.
  90. Louchet-Chauvet, A.; Farah, T.; Bodart, Q.; Clairon, A.; Landragin, A.; Merlet, S.; Santos, F.P.D. The influence of transverse motion within an atomic gravimeter. New J. Phys. 2011, 13, 065025.
  91. Schkolnik, V.; Leykauf, B.; Hauth, M.; Freier, C.; Peters, A. The effect of wavefront aberrations in atom interferometry. Appl. Phys. B 2015, 120, 311–316.
  92. Hu, J.; Chen, X.; Fang, J.; Zhou, L.; Zhong, J.; Wang, J.; Zhan, M. Analysis and suppression of wave-front-aberration phase noise in weak-equivalence-principle tests using dual-species atom interferometers. Phys. Rev. A 2017, 96, 023618.
  93. Wang, Z.; Chen, T.; Wang, X.; Zhang, Z.; Xu, Y.; Lin, Q. A precision analysis and determination of the technical requirements of an atom interferometer for gravity measurement. Front. Phys. China 2009, 4, 174–178.
  94. Zhou, M.; Luo, Q.; Chen, L.; Duan, X.; Hu, Z. Observing the effect of wave-front aberrations in an atom interferometer by modulating the diameter of Raman beams. Phys. Rev. A 2016, 93, 043610.
  95. Trimeche, A.; Langlois, M.; Merlet, S.; Pereira Dos Santos, F. Active Control of Laser Wavefronts in Atom Interferometers. Phys. Rev. Appl. 2017, 7, 034016.
  96. Karcher, R.; Imanaliev, A.; Merlet, S.; Santos, F.P.D. Improving the accuracy of atom interferometers with ultracold sources. New J. Phys. 2018, 20, 113041.
  97. Chamakhi, R.; Ahlers, H.; Telmini, M.; Schubert, C.; Rasel, E.M.; Gaaloul, N. Species-selective lattice launch for precision atom interferometry. New J. Phys. 2015, 17, 123002.
  98. Hu, Q.Q.; Freier, C.; Leykauf, B.; Schkolnik, V.; Yang, J.; Krutzik, M.; Peters, A. Mapping the absolute magnetic field and evaluating the quadratic Zeeman-effect-induced systematic error in an atom interferometer gravimeter. Phys. Rev. A 2017, 96, 033414.
  99. Wodey, E.; Tell, D.; Rasel, E.M.; Schlippert, D.; Baur, R.; Kissling, U.; Kölliker, B.; Lorenz, M.; Marrer, M.; Schläpfer, U.; et al. A scalable high-performance magnetic shield for very long baseline atom interferometry. Rev. Sci. Instrum. 2020, 91, 035117.
  100. Ji, Y.H.; Zhou, L.; Yan, S.T.; He, C.; Zhou, C.; Barthwal, S.; Yang, F.; Duan, W.T.; Zhang, W.D.; Xu, R.D.; et al. An actively compensated 8 nT-level magnetic shielding system for 10-m atom interferometer. Rev. Sci. Instrum. 2021, 92, 083201.
  101. Hobson, P.; Vovrosh, J.; Stray, B.; Packer, M.; Winch, J.; Holmes, N.; Hayati, F.; McGovern, K.; Bowtell, R.; Brookes, M.; et al. Bespoke magnetic field design for a magnetically shielded cold atom interferometer. Sci. Rep. 2022, 12, 10520.
  102. Jannin, R.; Cladé, P.; Guellati-Khélifa, S. Phase shift due to atom-atom interactions in a light-pulse atom interferometer. Phys. Rev. A 2015, 92, 013616.
  103. Horikoshi, M.; Nakagawa, K. Dephasing due to atom-atom interaction in a waveguide interferometer using a Bose-Einstein condensate. Phys. Rev. A 2006, 74, 031602.
  104. Yao, Z.; Solaro, C.; Carrez, C.; Cladé, P.; Guellati-Khelifa, S. Local phase shift due to interactions in an atom interferometer. Phys. Rev. A 2022, 106, 043312.
  105. Burchianti, A.; D’Errico, C.; Marconi, L.; Minardi, F.; Fort, C.; Modugno, M. Effect of interactions in the interference pattern of Bose-Einstein condensates. Phys. Rev. A 2020, 102, 043314.
  106. Zhang, H.; Mao, D.K.; Luo, Q.; Hu, Z.K.; Chen, L.L.; Zhou, M.K. The self-attraction effect in an atom gravity gradiometer. Metrologia 2020, 57, 045011.
  107. D’Agostino, G.; Merlet, S.; Landragin, A.; Santos, F.P.D. Perturbations of the local gravity field due to mass distribution on precise measuring instruments: A numerical method applied to a cold atom gravimeter. Metrologia 2011, 48, 299.
  108. Hensley, J.M.; Peters, A.; Chu, S. Active low frequency vertical vibration isolation. Rev. Sci. Instrum. 1999, 70, 2735–2741.
  109. Tang, B.; Zhou, L.; Xiong, Z.; Wang, J.; Zhan, M. A programmable broadband low frequency active vibration isolation system for atom interferometry. Rev. Sci. Instrum. 2014, 85, 093109.
  110. Zhou, M.K.; Xiong, X.; Chen, L.L.; Cui, J.F.; Duan, X.C.; Hu, Z.K. Note: A three-dimension active vibration isolator for precision atom gravimeters. Rev. Sci. Instrum. 2015, 86, 046108.
  111. Bonnin, A.; Zahzam, N.; Bidel, Y.; Bresson, A. Characterization of a simultaneous dual-species atom interferometer for a quantum test of the weak equivalence principle. Phys. Rev. A 2015, 92, 023626.
  112. Lévèque, T.; Gauguet, A.; Michaud, F.; Pereira Dos Santos, F.; Landragin, A. Enhancing the Area of a Raman Atom Interferometer Using a Versatile Double-Diffraction Technique. Phys. Rev. Lett. 2009, 103, 080405.
  113. Malossi, N.; Bodart, Q.; Merlet, S.; Lévèque, T.; Landragin, A.; Santos, F.P.D. Double diffraction in an atomic gravimeter. Phys. Rev. A 2010, 81, 013617.
  114. Zhou, L.; Long, S.; Tang, B.; Chen, X.; Gao, F.; Peng, W.; Duan, W.; Zhong, J.; Xiong, Z.; Wang, J.; et al. Test of Equivalence Principle at 10−8 Level by a Dual-Species Double-Diffraction Raman Atom Interferometer. Phys. Rev. Lett. 2015, 115, 013004.
  115. Deng, X.B.; Duan, X.C.; Mao, D.K.; Zhou, M.K.; Shao, C.G.; Hu, Z.K. Common-mode noise rejection using fringe-locking method in WEP test by simultaneous dual-species atom interferometers. Chin. Phys. B 2017, 26, 043702.
  116. Abend, S.; Allard, B.; Arnold, A.S.; Ban, T.; Barry, L.; Battelier, B.; Bawamia, A.; Beaufils, Q.; Bernon, S.; Bertoldi, A.; et al. Technology roadmap for cold-atoms based quantum inertial sensor in space. AVS Quantum Sci. 2023, 5, 019201.
  117. Schuldt, T.; Schubert, C.; Krutzik, M.; Bote, L.G.; Gaaloul, N.; Hartwig, J.; Ahlers, H.; Herr, W.; Posso-Trujillo, K.; Rudolph, J.; et al. Design of a dual species atom interferometer for space. Exp. Astron. 2015, 39, 167–206.
  118. Hinton, A.; Perea-Ortiz, M.; Winch, J.; Briggs, J.; Freer, S.; Moustoukas, D.; Powell-Gill, S.; Squire, C.; Lamb, A.; Rammeloo, C.; et al. A portable magneto-optical trap with prospects for atom interferometry in civil engineering. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160238.
  119. Lee, J.; Ding, R.; Christensen, J.; Rosenthal, R.R.; Ison, A.; Gillund, D.P.; Bossert, D.; Fuerschbach, K.H.; Kindel, W.; Finnegan, P.S.; et al. A compact cold-atom interferometer with a high data-rate grating magneto-optical trap and a photonic-integrated-circuit-compatible laser system. Nat. Commun. 2022, 13, 5131.
  120. Fang, J.; Hu, J.; Chen, X.; Zhu, H.; Zhou, L.; Zhong, J.; Wang, J.; Zhan, M. Realization of a compact one-seed laser system for atom interferometer-based gravimeters. Opt. Express 2018, 26, 1586–1596.
  121. Mazon, M.J.; Iyanu, G.H.; Wang, H. A Portable, Compact Cold Atom Physics Package for Atom Interferometry. In Proceedings of the 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC), Orlando, FL, USA, 14–18 April 2019; pp. 1–5.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback